人教版九年级上册22二次函数的小结与复习 课件 (共38张PPT)
文档属性
| 名称 | 人教版九年级上册22二次函数的小结与复习 课件 (共38张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 17:29:39 | ||
图片预览






文档简介
(共38张PPT)
二次函数的小结和复习
九年级 数学
学习目标:
二次函数的小结和复习
1. 通过复习二次函数的图象和性质,运用二次函数解决实际问题等内容,梳理本章知识,形成有关二次函数的知识体系.
2. 通过回顾探究二次函数的图象和性质的过程,再次体会类比归纳和数形结合的数学思想,形成分析和解决函数问题的一些基本方法.
3. 通过利用二次函数解决实际问题,再次体会建模思想,增强应用意识.
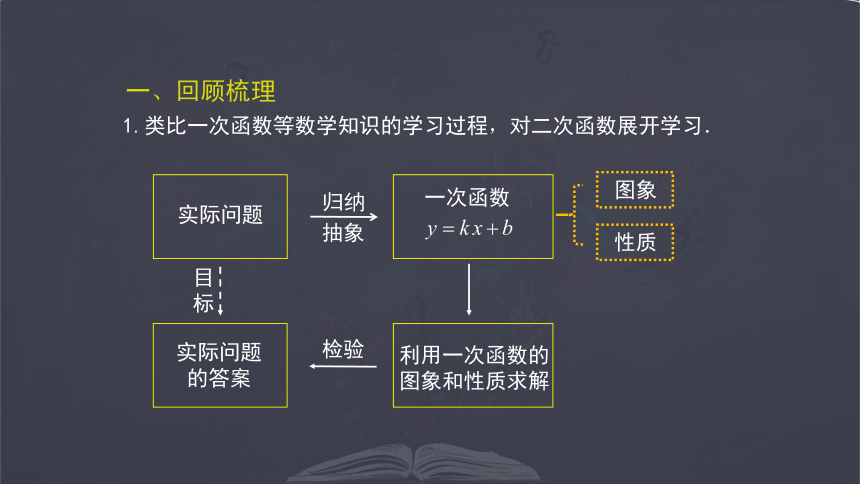
利用一次函数的
图象和性质求解
实际问题
的答案
一次函数
实际问题
目标
图象
性质
1.类比一次函数等数学知识的学习过程,对二次函数展开学习.
一、回顾梳理
归纳
抽象
检验
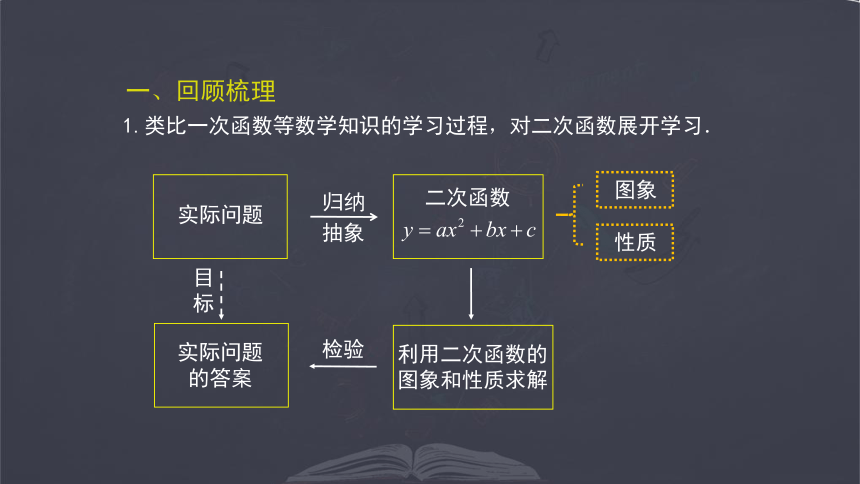
利用二次函数的
图象和性质求解
实际问题
的答案
二次函数
实际问题
1.类比一次函数等数学知识的学习过程,对二次函数展开学习.
图象
性质
目标
归纳
抽象
一、回顾梳理
检验
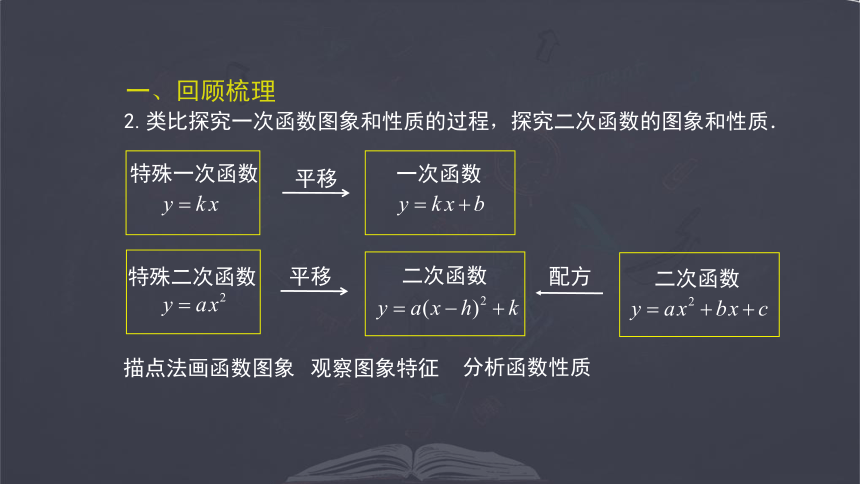
一次函数
特殊一次函数
特殊二次函数
二次函数
描点法画函数图象
二次函数
2.类比探究一次函数图象和性质的过程,探究二次函数的图象和性质.
配方
平移
观察图象特征
分析函数性质
平移
一、回顾梳理
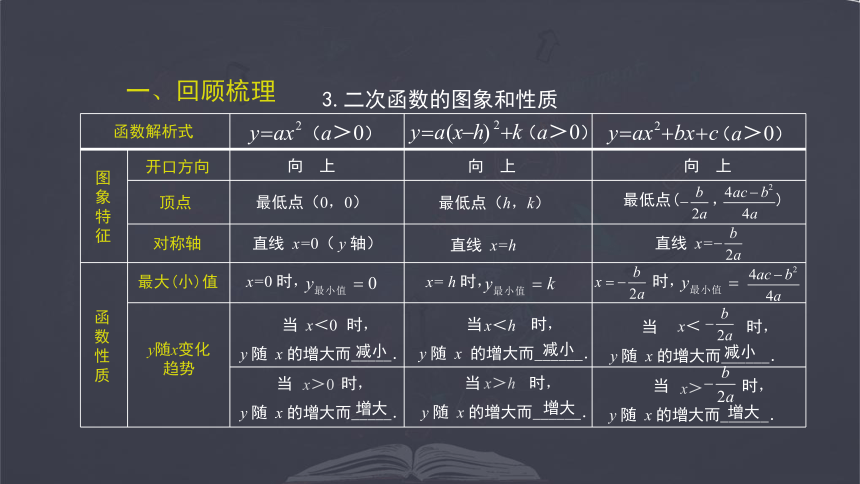
最低点( , )
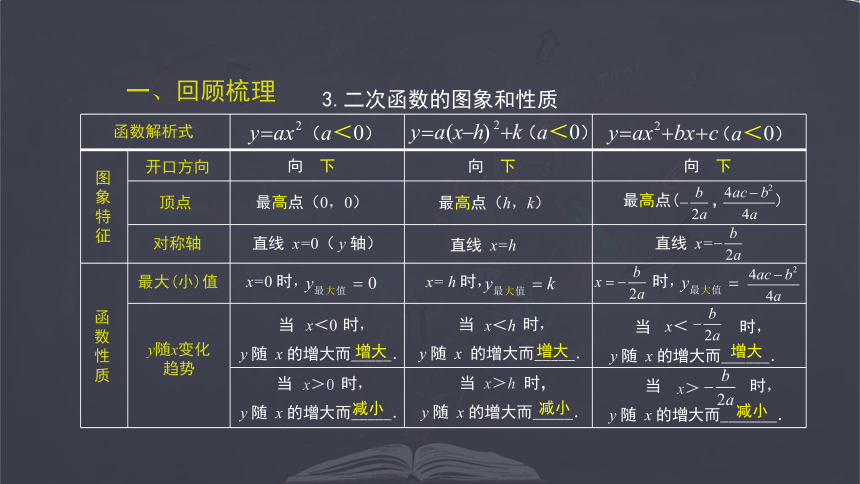
3.二次函数的图象和性质
一、回顾梳理
当 时,
y 随 x 的增大而____.
x>
函数解析式
图象特征
函数性质
开口方向
顶点
向 上
最大(小)值
y随x变化趋势
(a>0)
(a>0)
(a>0)
向 上
向 上
对称轴
最低点(0,0)
最低点(h,k)
直线 x=0( y 轴)
直线 x=h
直线 x=
x=0 时,
当 时,
y 随 x 的增大而_____.
x>0
当 时,
y 随 x 的增大而_____.
x<0
当 时,
y 随 x 的增大而______.
x<h
当 时,
y 随 x 的增大而______.
x>h
当 时,
y 随 x 的增大而_____.
x<
x= h 时,
时,
增大
减小
减小
减小
增大
增大
最高点( , )
3.二次函数的图象和性质
一、回顾梳理
当 时,
y 随 x 的增大而____.
x>
函数解析式
图象特征
函数性质
开口方向
顶点
向 下
最大(小)值
y随x变化趋势
(a<0)
(a<0)
(a<0)
向 下
向 下
对称轴
最高点(0,0)
最高点(h,k)
直线 x=0( y 轴)
直线 x=h
直线 x=
当 时,
y 随 x 的增大而_____.
x>0
当 时,
y 随 x 的增大而_____.
x<0
当 时,
y 随 x 的增大而_____.
x<h
当 时,
y 随 x 的增大而_____.
x>h
当 时,
y 随 x 的增大而_____.
x<
x= h 时,
时,
减小
增大
增大
增大
减小
减小
x=0 时,
4. 二次函数与一元二次方程
一、回顾梳理
2
1
0
无实数根
两个相等的实数根
两个不等的实数根
二次函数 的图象与x轴的公共点个数
一元二次方程
根的情况
一元二次方程
二次函数
已知函数值,求自变量的值
二次函数图象与x轴公共点的横坐标----相应一元二次方程的根
的取值范围
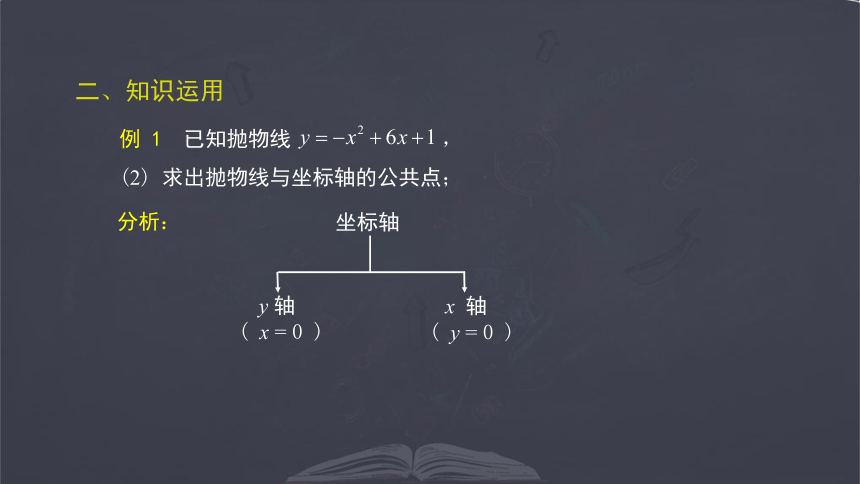
二、知识运用
例 1 已知抛物线 ,
(1) 求抛物线的开口方向,对称轴和顶点;
(2) 求出抛物线与坐标轴的公共点;
(3) 抛物线 可以看成抛物线 怎样平移得到的?
例 1 已知抛物线 ,
(1) 求抛物线的开口方向,对称轴和顶点;
分析:
开口方向----------
a的符号
顶点: ,
对称轴:直线
对称轴和顶点------
二、知识运用
解: a = -1,b = 6,c = 1.
∵a = -1<0 ,
∴抛物线开口向下.
∵ ,
∴对称轴是直线 x = 3.
∵ ,
∴顶点(3,10).
例 1 已知抛物线 ,
(1) 求抛物线的开口方向,对称轴和顶点;
二、知识运用
分析:
例 1 已知抛物线 ,
(2) 求出抛物线与坐标轴的公共点;
二、知识运用
坐标轴
x 轴
y 轴
( x = 0 )
( y = 0 )
当 y=0 时,
解得 , .
∴抛物线与x轴的公共点是
( , ),( , ).
解:当 x = 0 时,
.
∴抛物线与 y 轴的公共点是
(0,1).
例 1 已知抛物线 ,
⑵ 求出抛物线与坐标轴的公共点;
二、知识运用
例 1 已知抛物线 ,
⑶ 抛物线 可以看成抛物线 怎样平移得到的?
分析:
平移
平移
配方
配方
答:抛物线 可以看成抛物线 向上平移10个
单位长度,向右平移3个单位长度得到的.
二、知识运用
例 2 已知二次函数的解析式 ,
⑴ 若抛物线经过(-1,0),(3,0),求这条抛物线的解析式.
⑵ 若抛物线的对称轴是直线 x = 1 ,且经过(2, -3),
求这条抛物线的解析式.
⑶ 若 x,y 满足下表,求这条抛物线的解析式.
x … -1 0 2 3 …
y … 0 -3 -3 0 …
二、知识运用
分析:
两个待定的系数: b 和 c ,
例 2 已知二次函数的解析式 ,
⑴ 若抛物线经过(-1,0),(3,0),求这条抛物线的解析式.
二、知识运用
两个已知的点:(-1,0)和(3,0),
运用待定系数法求解析式.
例 2 已知二次函数的解析式 ,
⑴ 若抛物线经过(-1,0),(3,0),求这条抛物线的解析式.
二、知识运用
解得 ,
∴可得抛物线解析式
.
.
解:由题意可知函数图象经过
( -1 ,0),(3,0).
∴可得 ,
.
例 2 已知二次函数的解析式 ,
⑵ 若抛物线的对称轴是直线 x =1,且经过(2,-3),
求这条抛物线的解析式.
解:由题意可得
,
.
解得 ,
.
∴所求抛物线解析式
.
二、知识运用
例 2 已知二次函数的解析式 ,
⑶若 x,y 满足下表,求这条抛物线的解析式.
分析: 运用待定系数法求解析式(求出 b 和 c 的值即可).
(方法一)选取图象上的两个点的坐标,代入函数解析式,得到关于 b 和 c 的二元一次方程组.
二、知识运用
x … -1 0 2 3 …
y … 0 -3 -3 0 …
例 2 已知二次函数的解析式 ,
⑶ 若 x,y 满足下表,求这条抛物线的解析式.
x … -1 0 2 3 …
y … 0 -3 -3 0 …
二、知识运用
解得 ,
∴可得抛物线解析式
解:由题意可知函数图象经过
(-1,0),(0,-3).
∴可得 ,
.
.
.
例 2 已知二次函数的解析式 ,
⑶ 若 x,y 满足下表,求这条抛物线的解析式.
x … -1 0 2 3 …
y … 0 -3 -3 0 …
分析:运用待定系数法求解析式(求出 b 和 c 的值即可).
(方法二)运用抛物线的轴对称性.
二、知识运用
解:由题意可知函数图象经过
(0,-3).顶点横坐标为 ,
∴可得 ,
.
解得 ,
.
∴可得抛物线解析式
.
例 2 已知二次函数的解析式 ,
⑶ 若 x,y 满足下表,求这条抛物线的解析式.
x … -1 0 2 3 …
y … 0 -3 -3 0 …
二、知识运用
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑴ 写出月销售利润 y (单位:元)与售价 x (单位:元/千克)之间的函数关系式.
⑵ 当销售单价定为 55 元时,计算月销售量和销售利润.
⑶ 商店想在月销售成本不超过 10 000 元的情况下,使销售利润达到
8 000 元,销售单价应定为多少?
⑷ 当售价定为多少元时会获得最大利润,求出最大利润.
二、知识运用
每千克利润(元) 月销量(千克) 月销售利润(元)
涨价前
涨价后
50-40
y
↓10 千克
↑1元
500
(50-40) ×500
↑ 个1元
↓ 个 10 千克
(x-50)
分析:
(x-50)
50-40+(x-50)
500-10 (x-50)
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑴ 写出月销售利润 y (单位:元)与售价 x (单位:元/千克)之间的函数关系式.
二、知识运用
解:
∴ 函数关系式为 .
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑴ 写出月销售利润 y (单位:元)与售价 x (单位:元/千克)之间的函数关系式.
二、知识运用
分析:
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑵ 当销售单价定为 55 元时,计算月销售量和销售利润.
二、知识运用
每千克利润(元) 月销量(千克) 月销售利润(元)
涨价前
涨价后
50-40
y
500
(50-40) ×500
50-40+(x-50)
500-10 (x-50)
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑵ 当销售单价定为 55 元时,计算月销售量和销售利润.
解:
当x = 55时,
500 - ( x - 50 ) ·10 = 450.
∴ 当销售单价定为55元时,
月销售量是450千克,
销售利润6 750元.
二、知识运用
.
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑶ 商店想在月销售成本不超过 10 000 元的情况下,使销售利润达到
8 000 元,销售单价应定为多少?
解:
∵函数关系式为
有 ,
解得 , .
∴当 y= 8 000 时,
二、知识运用
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑶ 商店想在月销售成本不超过 10 000 元的情况下,使销售利润达到
8 000 元,销售单价应定为多少?
每千克利润 月销量 月销售利润
涨价后
y
50-40+(x-50)
500-(x-50) ·10
分析:
月销售成本=每千克成本×月销量=40×[500-(60-50)×10]=16 000>10 000
二、知识运用
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑶ 商店想在月销售成本不超过 10 000 元的情况下,使销售利润达到
8 000 元,销售单价应定为多少?
每千克利润 月销量 月销售利润
涨价后
y
50-40+(x-50)
500-(x-50) ·10
分析:
月销售成本=每千克成本×月销量=40×[500-(80-50)×10]=8 000<10 000
二、知识运用
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑶ 商店想在月销售成本不超过 10 000 元的情况下,使销售利润达到
8 000 元,销售单价应定为多少?
∵函数关系式为
,
∴当 y= 8 000 时,
解:
但 x= 60 时,月销售成本
40×[500-(60-50)×10]>10 000,
不合题意,舍.
∴销售单价应定为 80 元/千克.
解得 , .
,
二、知识运用
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑷ 当售价定为多少元时会获得最大利润,求出最大利润.
解:
∵
,
∴ 当售价定为 70 元时会获得最大利润,
最大利润是 90 000 元.
二、知识运用
例 4 如图所示,小明的父亲在相距 2 m 的两棵树上拴了一根绳子,给他做了个简易的秋千,拴绳子的地方离地面的高度都是 2.5 m,绳子自然下垂呈抛物线形,身高 1 m 的小明距较近的那棵树 0.5 m 时,头部刚好接触到绳子.
求绳子的最低点离地面的距离.
2.5 m
1 m
0.5 m
2 m
A
B
C
D
E
二、知识运用
例 4 如图所示,小明的父亲在相距 2 m 的两棵树上拴了一根绳子,给他做了个简易的秋千,拴绳子的地方离地面的高度都是 2.5 m,绳子自然下垂呈抛物线形,身高 1 m 的小明距较近的那棵树 0.5 m 时,头部刚好接触到绳子.
求绳子的最低点离地面的距离.
2.5 m
1 m
0.5 m
2 m
A
B
C
D
E
二、知识运用
O
y
x
分析:如图所示,以线段 DE 的中点为原点,
抛物线的对称轴为 y 轴,建立平面直角坐标系.
则 A(-1,2.5),B(1,2.5),C(-0.5,1).
O
y
x
2.5
1
1
-1
-0.5
A
B
C
D
E
例 4
二、知识运用
解:如图所示,以线段 DE 的中点为原点,
抛物线的对称轴为 y 轴,建立平面直角坐标系.
则 A(-1,2.5),B(1,2.5),C(-0.5,1).
设抛物线的解析式为 (-1≤x≤1).
当 x = 0 时,y = 0.5.
所以绳子的最低点离地面的距离为 0.5 m.
所以抛物线的解析式为 y = 2 x2 + 0.5.
把点 A,B 坐标代入解析式,得
,
解得
,
.
例 4
二、知识运用
解:如图所示,以线段 DE 的中点为原点,
抛物线的对称轴为 y 轴,建立平面直角坐标系.
则 A(-1,2.5),B(1,2.5),C(-0.5,1).
设抛物线的解析式为
当 x = 0 时,y = 0.5.
所以绳子的最低点离地面的距离为 0.5 m.
所以抛物线的解析式为 y = 2 x2 + 0.5.
把点 A,B 坐标代入解析式,得
解得
,
建立适当的坐标系
确定已知点的坐标
设解析式
代入已知点坐标得方程组
解方程组
求得解析式
待定系数法求解析式
求未知点坐标
得线段长
,
.
三、归纳小结
一元二次方程
y=0
目标
实际问题
的答案
利用二次函数的
图象和性质求解
二次函数
实际问题
抽象
归纳
类比
数形结合
从特殊到一般
模型思想
应用意识
归纳
化归
图象
性质
左右平移
上下平移
二次函数
左右平移
上下平移
二次函数
二次函数
二次函数
图形面积
抛物线形
销售利润
……
……
同学们再见
二次函数的小结和复习
九年级 数学
学习目标:
二次函数的小结和复习
1. 通过复习二次函数的图象和性质,运用二次函数解决实际问题等内容,梳理本章知识,形成有关二次函数的知识体系.
2. 通过回顾探究二次函数的图象和性质的过程,再次体会类比归纳和数形结合的数学思想,形成分析和解决函数问题的一些基本方法.
3. 通过利用二次函数解决实际问题,再次体会建模思想,增强应用意识.
利用一次函数的
图象和性质求解
实际问题
的答案
一次函数
实际问题
目标
图象
性质
1.类比一次函数等数学知识的学习过程,对二次函数展开学习.
一、回顾梳理
归纳
抽象
检验
利用二次函数的
图象和性质求解
实际问题
的答案
二次函数
实际问题
1.类比一次函数等数学知识的学习过程,对二次函数展开学习.
图象
性质
目标
归纳
抽象
一、回顾梳理
检验
一次函数
特殊一次函数
特殊二次函数
二次函数
描点法画函数图象
二次函数
2.类比探究一次函数图象和性质的过程,探究二次函数的图象和性质.
配方
平移
观察图象特征
分析函数性质
平移
一、回顾梳理
最低点( , )
3.二次函数的图象和性质
一、回顾梳理
当 时,
y 随 x 的增大而____.
x>
函数解析式
图象特征
函数性质
开口方向
顶点
向 上
最大(小)值
y随x变化趋势
(a>0)
(a>0)
(a>0)
向 上
向 上
对称轴
最低点(0,0)
最低点(h,k)
直线 x=0( y 轴)
直线 x=h
直线 x=
x=0 时,
当 时,
y 随 x 的增大而_____.
x>0
当 时,
y 随 x 的增大而_____.
x<0
当 时,
y 随 x 的增大而______.
x<h
当 时,
y 随 x 的增大而______.
x>h
当 时,
y 随 x 的增大而_____.
x<
x= h 时,
时,
增大
减小
减小
减小
增大
增大
最高点( , )
3.二次函数的图象和性质
一、回顾梳理
当 时,
y 随 x 的增大而____.
x>
函数解析式
图象特征
函数性质
开口方向
顶点
向 下
最大(小)值
y随x变化趋势
(a<0)
(a<0)
(a<0)
向 下
向 下
对称轴
最高点(0,0)
最高点(h,k)
直线 x=0( y 轴)
直线 x=h
直线 x=
当 时,
y 随 x 的增大而_____.
x>0
当 时,
y 随 x 的增大而_____.
x<0
当 时,
y 随 x 的增大而_____.
x<h
当 时,
y 随 x 的增大而_____.
x>h
当 时,
y 随 x 的增大而_____.
x<
x= h 时,
时,
减小
增大
增大
增大
减小
减小
x=0 时,
4. 二次函数与一元二次方程
一、回顾梳理
2
1
0
无实数根
两个相等的实数根
两个不等的实数根
二次函数 的图象与x轴的公共点个数
一元二次方程
根的情况
一元二次方程
二次函数
已知函数值,求自变量的值
二次函数图象与x轴公共点的横坐标----相应一元二次方程的根
的取值范围
二、知识运用
例 1 已知抛物线 ,
(1) 求抛物线的开口方向,对称轴和顶点;
(2) 求出抛物线与坐标轴的公共点;
(3) 抛物线 可以看成抛物线 怎样平移得到的?
例 1 已知抛物线 ,
(1) 求抛物线的开口方向,对称轴和顶点;
分析:
开口方向----------
a的符号
顶点: ,
对称轴:直线
对称轴和顶点------
二、知识运用
解: a = -1,b = 6,c = 1.
∵a = -1<0 ,
∴抛物线开口向下.
∵ ,
∴对称轴是直线 x = 3.
∵ ,
∴顶点(3,10).
例 1 已知抛物线 ,
(1) 求抛物线的开口方向,对称轴和顶点;
二、知识运用
分析:
例 1 已知抛物线 ,
(2) 求出抛物线与坐标轴的公共点;
二、知识运用
坐标轴
x 轴
y 轴
( x = 0 )
( y = 0 )
当 y=0 时,
解得 , .
∴抛物线与x轴的公共点是
( , ),( , ).
解:当 x = 0 时,
.
∴抛物线与 y 轴的公共点是
(0,1).
例 1 已知抛物线 ,
⑵ 求出抛物线与坐标轴的公共点;
二、知识运用
例 1 已知抛物线 ,
⑶ 抛物线 可以看成抛物线 怎样平移得到的?
分析:
平移
平移
配方
配方
答:抛物线 可以看成抛物线 向上平移10个
单位长度,向右平移3个单位长度得到的.
二、知识运用
例 2 已知二次函数的解析式 ,
⑴ 若抛物线经过(-1,0),(3,0),求这条抛物线的解析式.
⑵ 若抛物线的对称轴是直线 x = 1 ,且经过(2, -3),
求这条抛物线的解析式.
⑶ 若 x,y 满足下表,求这条抛物线的解析式.
x … -1 0 2 3 …
y … 0 -3 -3 0 …
二、知识运用
分析:
两个待定的系数: b 和 c ,
例 2 已知二次函数的解析式 ,
⑴ 若抛物线经过(-1,0),(3,0),求这条抛物线的解析式.
二、知识运用
两个已知的点:(-1,0)和(3,0),
运用待定系数法求解析式.
例 2 已知二次函数的解析式 ,
⑴ 若抛物线经过(-1,0),(3,0),求这条抛物线的解析式.
二、知识运用
解得 ,
∴可得抛物线解析式
.
.
解:由题意可知函数图象经过
( -1 ,0),(3,0).
∴可得 ,
.
例 2 已知二次函数的解析式 ,
⑵ 若抛物线的对称轴是直线 x =1,且经过(2,-3),
求这条抛物线的解析式.
解:由题意可得
,
.
解得 ,
.
∴所求抛物线解析式
.
二、知识运用
例 2 已知二次函数的解析式 ,
⑶若 x,y 满足下表,求这条抛物线的解析式.
分析: 运用待定系数法求解析式(求出 b 和 c 的值即可).
(方法一)选取图象上的两个点的坐标,代入函数解析式,得到关于 b 和 c 的二元一次方程组.
二、知识运用
x … -1 0 2 3 …
y … 0 -3 -3 0 …
例 2 已知二次函数的解析式 ,
⑶ 若 x,y 满足下表,求这条抛物线的解析式.
x … -1 0 2 3 …
y … 0 -3 -3 0 …
二、知识运用
解得 ,
∴可得抛物线解析式
解:由题意可知函数图象经过
(-1,0),(0,-3).
∴可得 ,
.
.
.
例 2 已知二次函数的解析式 ,
⑶ 若 x,y 满足下表,求这条抛物线的解析式.
x … -1 0 2 3 …
y … 0 -3 -3 0 …
分析:运用待定系数法求解析式(求出 b 和 c 的值即可).
(方法二)运用抛物线的轴对称性.
二、知识运用
解:由题意可知函数图象经过
(0,-3).顶点横坐标为 ,
∴可得 ,
.
解得 ,
.
∴可得抛物线解析式
.
例 2 已知二次函数的解析式 ,
⑶ 若 x,y 满足下表,求这条抛物线的解析式.
x … -1 0 2 3 …
y … 0 -3 -3 0 …
二、知识运用
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑴ 写出月销售利润 y (单位:元)与售价 x (单位:元/千克)之间的函数关系式.
⑵ 当销售单价定为 55 元时,计算月销售量和销售利润.
⑶ 商店想在月销售成本不超过 10 000 元的情况下,使销售利润达到
8 000 元,销售单价应定为多少?
⑷ 当售价定为多少元时会获得最大利润,求出最大利润.
二、知识运用
每千克利润(元) 月销量(千克) 月销售利润(元)
涨价前
涨价后
50-40
y
↓10 千克
↑1元
500
(50-40) ×500
↑ 个1元
↓ 个 10 千克
(x-50)
分析:
(x-50)
50-40+(x-50)
500-10 (x-50)
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑴ 写出月销售利润 y (单位:元)与售价 x (单位:元/千克)之间的函数关系式.
二、知识运用
解:
∴ 函数关系式为 .
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑴ 写出月销售利润 y (单位:元)与售价 x (单位:元/千克)之间的函数关系式.
二、知识运用
分析:
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑵ 当销售单价定为 55 元时,计算月销售量和销售利润.
二、知识运用
每千克利润(元) 月销量(千克) 月销售利润(元)
涨价前
涨价后
50-40
y
500
(50-40) ×500
50-40+(x-50)
500-10 (x-50)
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑵ 当销售单价定为 55 元时,计算月销售量和销售利润.
解:
当x = 55时,
500 - ( x - 50 ) ·10 = 450.
∴ 当销售单价定为55元时,
月销售量是450千克,
销售利润6 750元.
二、知识运用
.
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑶ 商店想在月销售成本不超过 10 000 元的情况下,使销售利润达到
8 000 元,销售单价应定为多少?
解:
∵函数关系式为
有 ,
解得 , .
∴当 y= 8 000 时,
二、知识运用
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑶ 商店想在月销售成本不超过 10 000 元的情况下,使销售利润达到
8 000 元,销售单价应定为多少?
每千克利润 月销量 月销售利润
涨价后
y
50-40+(x-50)
500-(x-50) ·10
分析:
月销售成本=每千克成本×月销量=40×[500-(60-50)×10]=16 000>10 000
二、知识运用
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑶ 商店想在月销售成本不超过 10 000 元的情况下,使销售利润达到
8 000 元,销售单价应定为多少?
每千克利润 月销量 月销售利润
涨价后
y
50-40+(x-50)
500-(x-50) ·10
分析:
月销售成本=每千克成本×月销量=40×[500-(80-50)×10]=8 000<10 000
二、知识运用
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑶ 商店想在月销售成本不超过 10 000 元的情况下,使销售利润达到
8 000 元,销售单价应定为多少?
∵函数关系式为
,
∴当 y= 8 000 时,
解:
但 x= 60 时,月销售成本
40×[500-(60-50)×10]>10 000,
不合题意,舍.
∴销售单价应定为 80 元/千克.
解得 , .
,
二、知识运用
例 3 某商店销售一种成本为 40 元/千克的水产品,若按 50 元/千克销售,一个月可售出 500 千克.销售价每涨 1 元,月销售量减少 10 千克.
⑷ 当售价定为多少元时会获得最大利润,求出最大利润.
解:
∵
,
∴ 当售价定为 70 元时会获得最大利润,
最大利润是 90 000 元.
二、知识运用
例 4 如图所示,小明的父亲在相距 2 m 的两棵树上拴了一根绳子,给他做了个简易的秋千,拴绳子的地方离地面的高度都是 2.5 m,绳子自然下垂呈抛物线形,身高 1 m 的小明距较近的那棵树 0.5 m 时,头部刚好接触到绳子.
求绳子的最低点离地面的距离.
2.5 m
1 m
0.5 m
2 m
A
B
C
D
E
二、知识运用
例 4 如图所示,小明的父亲在相距 2 m 的两棵树上拴了一根绳子,给他做了个简易的秋千,拴绳子的地方离地面的高度都是 2.5 m,绳子自然下垂呈抛物线形,身高 1 m 的小明距较近的那棵树 0.5 m 时,头部刚好接触到绳子.
求绳子的最低点离地面的距离.
2.5 m
1 m
0.5 m
2 m
A
B
C
D
E
二、知识运用
O
y
x
分析:如图所示,以线段 DE 的中点为原点,
抛物线的对称轴为 y 轴,建立平面直角坐标系.
则 A(-1,2.5),B(1,2.5),C(-0.5,1).
O
y
x
2.5
1
1
-1
-0.5
A
B
C
D
E
例 4
二、知识运用
解:如图所示,以线段 DE 的中点为原点,
抛物线的对称轴为 y 轴,建立平面直角坐标系.
则 A(-1,2.5),B(1,2.5),C(-0.5,1).
设抛物线的解析式为 (-1≤x≤1).
当 x = 0 时,y = 0.5.
所以绳子的最低点离地面的距离为 0.5 m.
所以抛物线的解析式为 y = 2 x2 + 0.5.
把点 A,B 坐标代入解析式,得
,
解得
,
.
例 4
二、知识运用
解:如图所示,以线段 DE 的中点为原点,
抛物线的对称轴为 y 轴,建立平面直角坐标系.
则 A(-1,2.5),B(1,2.5),C(-0.5,1).
设抛物线的解析式为
当 x = 0 时,y = 0.5.
所以绳子的最低点离地面的距离为 0.5 m.
所以抛物线的解析式为 y = 2 x2 + 0.5.
把点 A,B 坐标代入解析式,得
解得
,
建立适当的坐标系
确定已知点的坐标
设解析式
代入已知点坐标得方程组
解方程组
求得解析式
待定系数法求解析式
求未知点坐标
得线段长
,
.
三、归纳小结
一元二次方程
y=0
目标
实际问题
的答案
利用二次函数的
图象和性质求解
二次函数
实际问题
抽象
归纳
类比
数形结合
从特殊到一般
模型思想
应用意识
归纳
化归
图象
性质
左右平移
上下平移
二次函数
左右平移
上下平移
二次函数
二次函数
二次函数
图形面积
抛物线形
销售利润
……
……
同学们再见
同课章节目录
