1.4.1(第二课时)空间向量研究直线、平面平行 课件(共21张PPT)
文档属性
| 名称 | 1.4.1(第二课时)空间向量研究直线、平面平行 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 00:00:00 | ||
图片预览





文档简介
(共21张PPT)
空间向量与立体几何
1.4.1空间向量研究直线、平面平行
复习回顾
问题1 如何求直线的方向向量与平面的法向量?
(1)建系
(2)算点
(3)取向量
(4)建方程组
(5)取解
(1)设两点
(2)取向量
(1)算点,设法
(2)取向量:面内两个不共线向量
(3)建方程组
(4)取解
新知导入
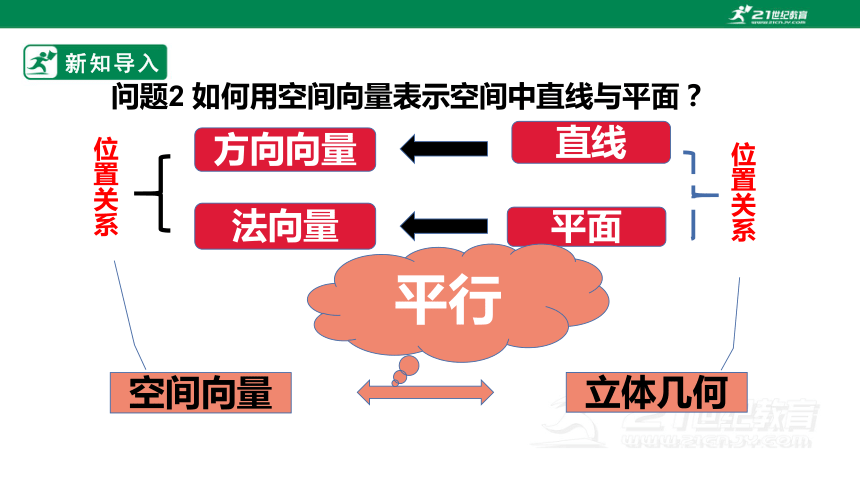
问题2 如何用空间向量表示空间中直线与平面?
直线
平面
方向向量
位置关系
位置关系
法向量
空间向量
立体几何
平行
教学目标
一
二
三
教学目标
用向量语言描述线线、线面、面面平行的关系
用向量语言证明直线、平面平行的相关判定定理
用向量语言解决立体几何直线、平面平行的相关问题
重点
难点
重点
新知探究
探究一:由直线、平面平行的关系,可以得到直线的方向向量、平面的法向量之间有什么关系?
新知讲解
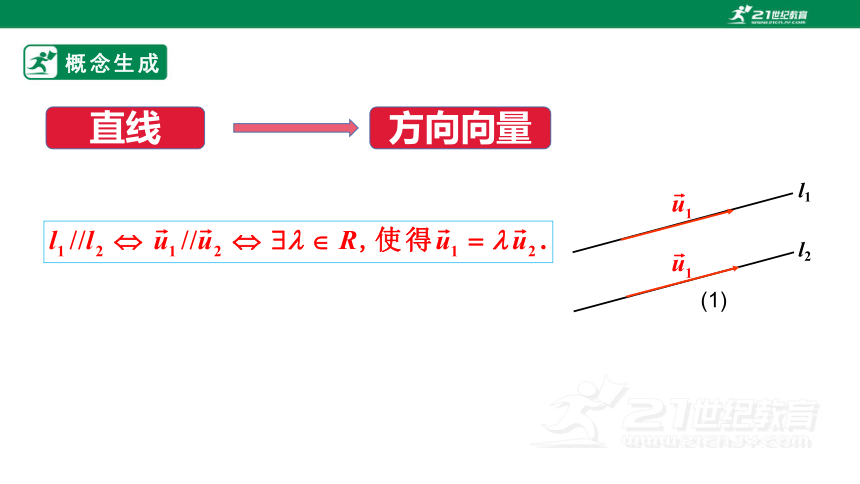
问题3 由直线与直线平行的关系,可以得到这两条直线的方向向量有什么关系?
l1
l2
(1)
如图(1)所示,设分别是直线l1, l2的方向向量,由方向向量的定义可知,如果两条直线平行,那么它们的方向向量一定平行,反过来,如果两条直线的方向向量平行,那么这两条直线也平行
概念生成
直线
方向向量
l1
l2
(1)
新知讲解
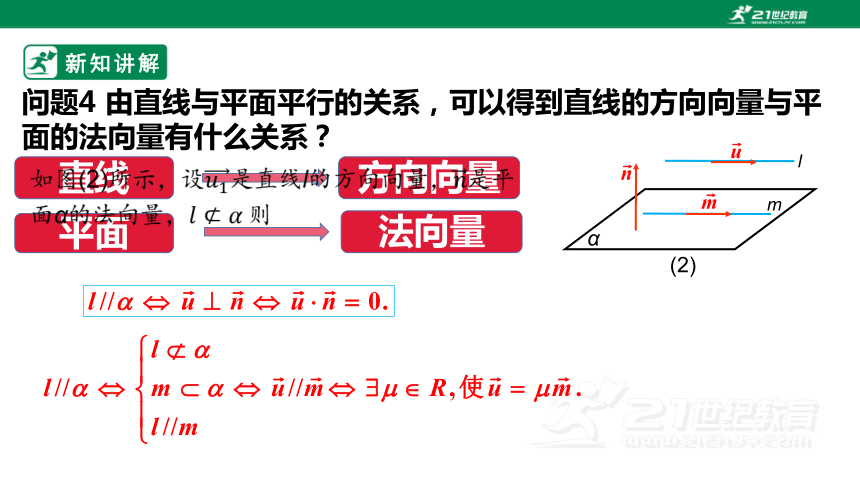
问题4 由直线与平面平行的关系,可以得到直线的方向向量与平面的法向量有什么关系?
直线
方向向量
平面
法向量
如图(2)所示,设是直线l的方向向量,是平面α的法向量,则
α
l
(2)
m
概念生成
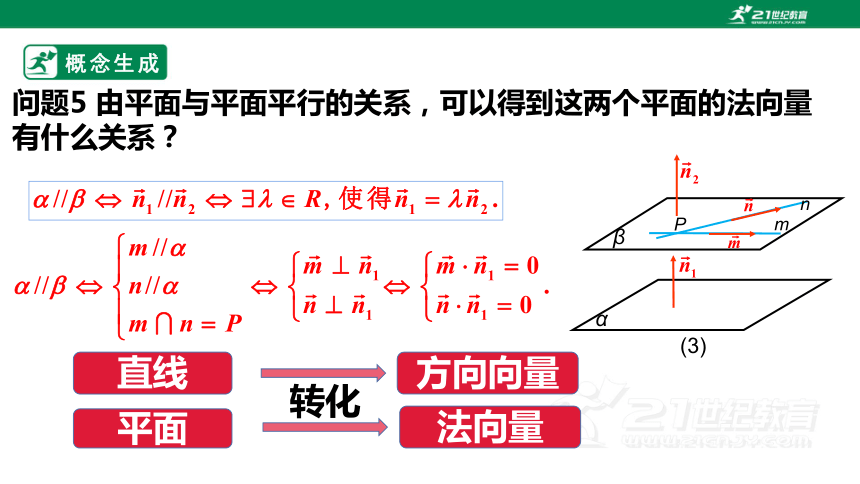
问题5 由平面与平面平行的关系,可以得到这两个平面的法向量有什么关系?
α
(3)
β
P
m
n
直线
方向向量
平面
法向量
转化
新知探究
探究二:用向量的方法证明直线、平面平行相关的判定定理
新知讲解
(1)证明“平面与平面平行的判定定理”
(2)证明“直线与平面平行的判定定理”
要求:
1.以小组形式进行讨论;
2.转化成数学语言,利用向量方法解释(数形结合)
3.总结方法
概念生成
(1)证明“平面与平面平行的判定定理”
α
β
P
b
a
换句话:两个平面的法向量共线
概念生成
(2)证明“直线与平面平行的判定定理”
α
b
a
换句话:法向量与方向向量垂直
新知探究
探究三:利用空间向量方法解决立体几何中直线、平面平行的相关问题
课堂练习
A
B
C
D
D1
A1
B1
C1
x
y
z
P
新知讲解
A
B
C
D
D1
A1
B1
C1
x
y
z
P
建系
设点
取向量
列方程组
取解
得结果
概念生成
建系
设点
取向量
方法总结
建系
设点
取向量
通用
列方程组
取解
法向量
取两点
得向量
方向向量
运算
课堂总结
线线平行
线面平行
面面平行
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
空间向量与立体几何
1.4.1空间向量研究直线、平面平行
复习回顾
问题1 如何求直线的方向向量与平面的法向量?
(1)建系
(2)算点
(3)取向量
(4)建方程组
(5)取解
(1)设两点
(2)取向量
(1)算点,设法
(2)取向量:面内两个不共线向量
(3)建方程组
(4)取解
新知导入
问题2 如何用空间向量表示空间中直线与平面?
直线
平面
方向向量
位置关系
位置关系
法向量
空间向量
立体几何
平行
教学目标
一
二
三
教学目标
用向量语言描述线线、线面、面面平行的关系
用向量语言证明直线、平面平行的相关判定定理
用向量语言解决立体几何直线、平面平行的相关问题
重点
难点
重点
新知探究
探究一:由直线、平面平行的关系,可以得到直线的方向向量、平面的法向量之间有什么关系?
新知讲解
问题3 由直线与直线平行的关系,可以得到这两条直线的方向向量有什么关系?
l1
l2
(1)
如图(1)所示,设分别是直线l1, l2的方向向量,由方向向量的定义可知,如果两条直线平行,那么它们的方向向量一定平行,反过来,如果两条直线的方向向量平行,那么这两条直线也平行
概念生成
直线
方向向量
l1
l2
(1)
新知讲解
问题4 由直线与平面平行的关系,可以得到直线的方向向量与平面的法向量有什么关系?
直线
方向向量
平面
法向量
如图(2)所示,设是直线l的方向向量,是平面α的法向量,则
α
l
(2)
m
概念生成
问题5 由平面与平面平行的关系,可以得到这两个平面的法向量有什么关系?
α
(3)
β
P
m
n
直线
方向向量
平面
法向量
转化
新知探究
探究二:用向量的方法证明直线、平面平行相关的判定定理
新知讲解
(1)证明“平面与平面平行的判定定理”
(2)证明“直线与平面平行的判定定理”
要求:
1.以小组形式进行讨论;
2.转化成数学语言,利用向量方法解释(数形结合)
3.总结方法
概念生成
(1)证明“平面与平面平行的判定定理”
α
β
P
b
a
换句话:两个平面的法向量共线
概念生成
(2)证明“直线与平面平行的判定定理”
α
b
a
换句话:法向量与方向向量垂直
新知探究
探究三:利用空间向量方法解决立体几何中直线、平面平行的相关问题
课堂练习
A
B
C
D
D1
A1
B1
C1
x
y
z
P
新知讲解
A
B
C
D
D1
A1
B1
C1
x
y
z
P
建系
设点
取向量
列方程组
取解
得结果
概念生成
建系
设点
取向量
方法总结
建系
设点
取向量
通用
列方程组
取解
法向量
取两点
得向量
方向向量
运算
课堂总结
线线平行
线面平行
面面平行
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
