北师大版九年级上册 4图形的相似复习课件(共15张PPT)
文档属性
| 名称 | 北师大版九年级上册 4图形的相似复习课件(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 490.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 17:33:29 | ||
图片预览





文档简介
(共15张PPT)
相似形
复习课
一.相似三角形的及相关概念
1.概念:对应角相等,对应边成比例
2.相似比:对应边长度的比,一般用k表示
3.全等三角形是相似三角形的特例,相似比为1
书写规范
1.书写两个三角形相似时,要注意对应点位置一致
2.相似比是有顺序的,△ABC~△A1B1C1,相似比为k,则△A1B1C1~△ABC,则相似比为
2
0
1
8
A+
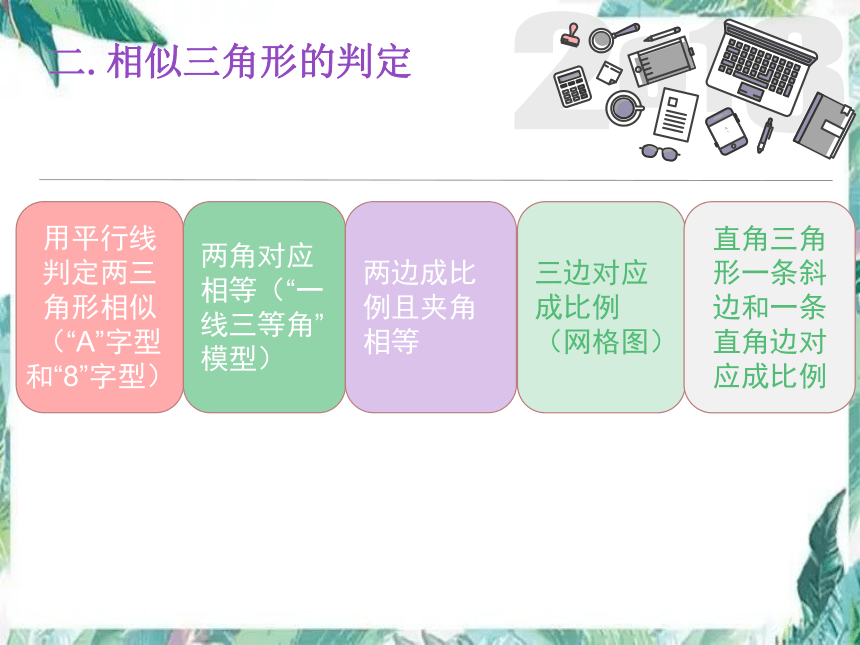
二.相似三角形的判定
用平行线判定两三角形相似(“A”字型和“8”字型)
两角对应相等(“一线三等角”模型)
两边成比例且夹角相等
三边对应成比例(网格图)
直角三角形一条斜边和一条直角边对应成比例
一个三角形的三边分别是3cm,4cm,6cm,与它相似的另外一个三角形的最大边是12cm,则另外两边的长是( )
知识点应用
如图,AB是斜靠在墙上的长梯,梯角B距离 墙1.4m,梯上D距离墙1.2m,BD长0.5m,则梯子的长为( )
A.3.2m B.4m C.3.5m D.4.2m
A
B
C
D
E
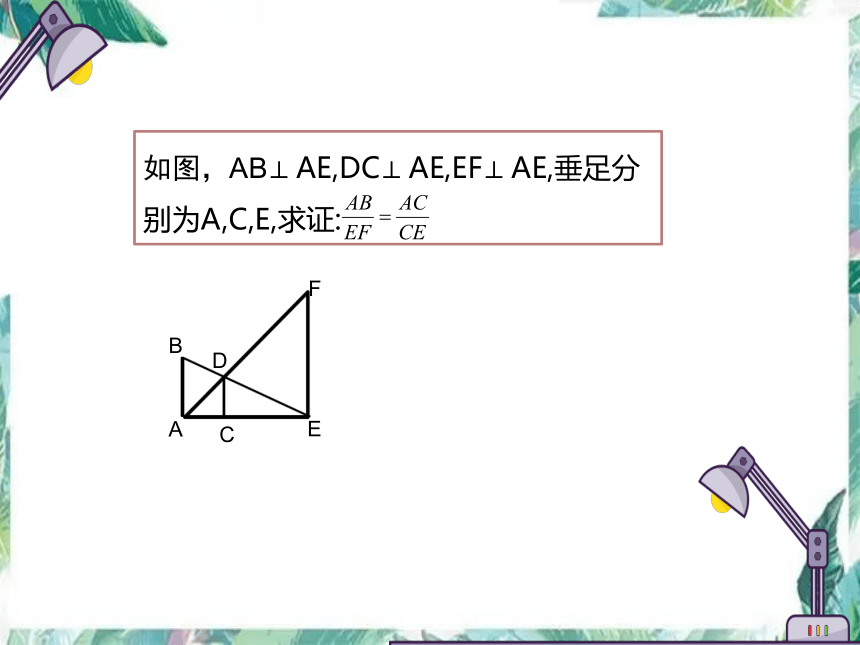
如图,AB AE,DC AE,EF AE,垂足分别为A,C,E,求证:
A
B
C
D
E
F
如图,△ABC 是一块锐角三角形材料,边 BC=120 mm,高 AD=80 mm,
要把它加工成正方形零件,使正方形的一边在 BC 上,其余两个顶点分别
在 AB、AC 上,这个正方形零件的边长是多少?
A
E
B
H
G
M
F
D
C
如图所示,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长是多少?
A
B
C
D
E
如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有( )
A.1条 B.2条 C.3条 D.4条
A
B
C
M
如图,在正方形ABCD中,E是BC上的一点,连接AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.求证:
(1)CG=BH;(2)FC2=BF GF;(3)
如图,在大小为4×4的正方形网格中,是相似三
角形的是 ( )
②
①
③
④
A. ①和② B. ②和③
C. ①和③ D. ②和④
如图,已知 △ABC中,D 为边 AC 上一点,P 为边
AB上一点,AB = 12,AC = 8,AD = 6,当 AP 的长
度为 时,△ADP 和 △ABC 相似.
A
B
C
D
4 或 9
如图,∠ABC=∠ADC=90°,AC= ,AD=2,当AB的长为多少时,这两个直角三角形相似?
A
B
C
D
∟
∟
努力
遇见美好
相似形
复习课
一.相似三角形的及相关概念
1.概念:对应角相等,对应边成比例
2.相似比:对应边长度的比,一般用k表示
3.全等三角形是相似三角形的特例,相似比为1
书写规范
1.书写两个三角形相似时,要注意对应点位置一致
2.相似比是有顺序的,△ABC~△A1B1C1,相似比为k,则△A1B1C1~△ABC,则相似比为
2
0
1
8
A+
二.相似三角形的判定
用平行线判定两三角形相似(“A”字型和“8”字型)
两角对应相等(“一线三等角”模型)
两边成比例且夹角相等
三边对应成比例(网格图)
直角三角形一条斜边和一条直角边对应成比例
一个三角形的三边分别是3cm,4cm,6cm,与它相似的另外一个三角形的最大边是12cm,则另外两边的长是( )
知识点应用
如图,AB是斜靠在墙上的长梯,梯角B距离 墙1.4m,梯上D距离墙1.2m,BD长0.5m,则梯子的长为( )
A.3.2m B.4m C.3.5m D.4.2m
A
B
C
D
E
如图,AB AE,DC AE,EF AE,垂足分别为A,C,E,求证:
A
B
C
D
E
F
如图,△ABC 是一块锐角三角形材料,边 BC=120 mm,高 AD=80 mm,
要把它加工成正方形零件,使正方形的一边在 BC 上,其余两个顶点分别
在 AB、AC 上,这个正方形零件的边长是多少?
A
E
B
H
G
M
F
D
C
如图所示,在边长为9的正三角形ABC中,BD=3,∠ADE=60°,则AE的长是多少?
A
B
C
D
E
如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有( )
A.1条 B.2条 C.3条 D.4条
A
B
C
M
如图,在正方形ABCD中,E是BC上的一点,连接AE,作BF⊥AE,垂足为H,交CD于F,作CG∥AE,交BF于G.求证:
(1)CG=BH;(2)FC2=BF GF;(3)
如图,在大小为4×4的正方形网格中,是相似三
角形的是 ( )
②
①
③
④
A. ①和② B. ②和③
C. ①和③ D. ②和④
如图,已知 △ABC中,D 为边 AC 上一点,P 为边
AB上一点,AB = 12,AC = 8,AD = 6,当 AP 的长
度为 时,△ADP 和 △ABC 相似.
A
B
C
D
4 或 9
如图,∠ABC=∠ADC=90°,AC= ,AD=2,当AB的长为多少时,这两个直角三角形相似?
A
B
C
D
∟
∟
努力
遇见美好
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
