北师大版九年级上册 2一元二次方程复习课件(共29张PPT)
文档属性
| 名称 | 北师大版九年级上册 2一元二次方程复习课件(共29张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 255.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 17:35:52 | ||
图片预览







文档简介
(共29张PPT)
一元二次方程
复习(1)
一元二次方程应用的一般步骤:
1.审(题);
2.找(数量关系);
3.设(未知数);
4.列(出方程);
5.解(方程);
6.检(验根的合理性);
7.答(写出答案).
一、复习回顾
1.一件商品的原价是100元,经过两次提价后的
价格为121元,如果每次提价的百分率都是x,根据题意,下面列出的方程正确的是( )
A.100(1+x)=121; B.100(1-x)=121;
C.100(1+x)2=121; D.100(1-x)2=121.
C
二、尝试解决
若平均增长(或降低)百分率都是x,
增长(或降低)前的量是a,
增长(或降低)n次后的量是b,
则他们的数量关系可表示为a(1±x)n=b.
二、尝试解决
2.如图,某中学准备在校园里利用围墙的一段,
再砌三面墙,围成一个矩形花园ABCD( 围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2.
二、尝试解决
解:设AB的长为x m,
则BC=(50-2x)m,
x(50-2x)=300,
解得x1=10,x2=15.
注意围墙的长度
当x=10时,BC=30>25,
∴不符合题意,舍去.
∴当x=15m,BC=20m时,矩形花园的面积为300m2.
二、尝试解决
x
50-2x
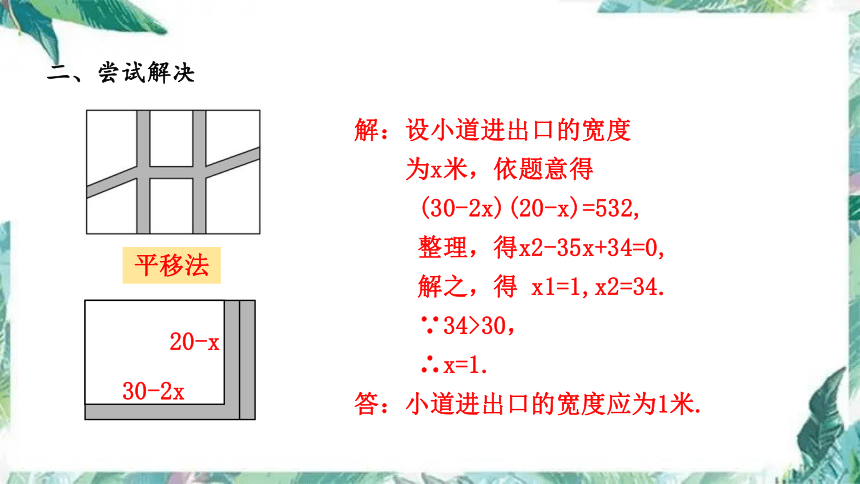
3.某单位准备将院内一块长30 m,宽20 m的长方形
空地,建成一个矩形花园.要求在花园中修两条纵向
平行和一条横向弯折的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532 m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)
二、尝试解决
解:设小道进出口的宽度
为x米,依题意得
(30-2x)(20-x)=532,
整理,得x2-35x+34=0,
解之,得 x1=1,x2=34.
∵34>30,
∴x=1.
答:小道进出口的宽度应为1米.
30-2x
20-x
平移法
二、尝试解决
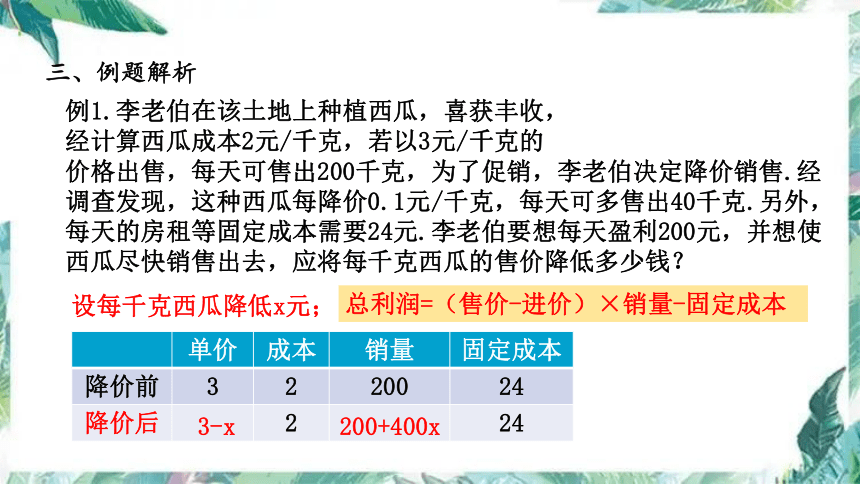
例1.李老伯在该土地上种植西瓜,喜获丰收,
经计算西瓜成本2元/千克,若以3元/千克的
价格出售,每天可售出200千克,为了促销,李老伯决定降价销售.经调查发现,这种西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本需要24元.李老伯要想每天盈利200元,并想使西瓜尽快销售出去,应将每千克西瓜的售价降低多少钱?
设每千克西瓜降低x元;
总利润=(售价-进价)×销量-固定成本
三、例题解析
单价 成本 销量 固定成本
降价前 3 2 200 24
降价后 2 24
3-x
200+400x
解:设每千克西瓜降低x元,
(3-x-2)(200+400x)-24=200,
解之,得 x1=0.2,x2=0.3.
∵为使西瓜尽快销售出去,
∴x=0.3.
答:每千克西瓜的售价降低0.3元.
三、例题解析
例1.李老伯在该土地上种植西瓜,喜获丰收,
经计算西瓜成本2元/千克,若以3元/千克的
价格出售,每天可售出200千克,为了促销,李老伯决定降价销售.经调查发现,这种西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本需要24元.李老伯要想每天盈利200元,并想使西瓜尽快销售出去,应将每千克西瓜的售价降低多少钱?
例如,在绿地中间开辟一个矩形的花圃,使四周的绿地等宽,绿地的面积与花圃的面积相等,你能计算出剩余绿地的宽吗?
例2:在一块长是32m、宽24m的矩形绿地内,要围
出一个花圃,使花圃面积是矩形面积的一半,你能给出设计方案吗?
三、例题解析
例如,在绿地中间开辟一个矩形的花圃,使四周的绿地等宽,绿地的面积与花圃的面积相等,你能计算出剩余绿地的宽吗?
例2:在一块长是32m、宽24m的矩形绿地内,要围
出一个花圃,使花圃面积是矩形面积的一半,你能给出设计方案吗?
x
解:设剩余绿地的等宽长为xm,
x
三、例题解析
32
24
例如,在绿地中间开辟一个矩形的花圃,使四周的绿地等宽,绿地的面积与花圃的面积相等,你能计算出剩余绿地的宽吗?
例2:在一块长是32m、宽24m的矩形绿地内,要围
出一个花圃,使花圃面积是矩形面积的一半,你能给出设计方案吗?
(32-2x)(24-2x)=×32×24,
解得,x1=4,x2=24(舍).
答:绿地的宽为4m.
x
解:设剩余绿地的等宽长为xm,
x
三、例题解析
32
24
例3.如图,在矩形中ABCD,AB=6cm,BC=12cm,
点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动.
(1)几秒钟后△DPQ的面积等于31cm2;
x
2x
6-x
12-2x
三、例题解析
解:设x秒后△DPQ的
面积为31cm2,
则AP=xcm,BP=(6-x)cm,
BQ=2xcm,CQ=(12-2x)cm,
由题意得:
6×12-0.5×12x-0.5×6(12-2x)
-0.5(6-x)2x=31,
整理,得x2-6x+8=0,
解之得 x1=1,x2=5.
答:1s或5s后△DPQ的面积为31cm2.
三、例题解析
x
2x
6-x
12-2x
解:设x秒后△DPQ的
面积为31cm2,
则AP=xcm,BP=(6-x)cm,
BQ=2xcm,CQ=(12-2x)cm,
由题意得:
0.5×12x+0.5×6(12-2x)+0.5(6-x)2x=41,
解之得 x1=1,x2=5.
答:1s或5s后△DPQ的面积为31cm2.
九年级数学名师课程
三、例题解析
x
2x
6-x
12-2x
三、例题解析
例3.(2)在运动过程中,是否存在这样的时刻,
使以点QP=QD.若存在,求出运动时间;若不存在,请说明理由.
x
2x
6-x
12-2x
假设运动开始后第x秒时,满足QP=QD,
∵QP2=PB2+BQ2=(6-x)2+(2x)2,
QD2=QC2+CD2=(12-2x)+62,
∴(12-2x)2+62=(6-x)2+(2x)2,
∴ x2+36x-144=0,
∴ x1=-18+6 ,x2=-18-6.
∵0<-18+6<6 ,∴x=-18+6.
三、例题解析
例3.(2)在运动过程中,是否存在这样的时刻,
使以点QP=QD.若存在,求出运动时间;若不存在,请说明理由.
x
2x
6-x
12-2x
1.一个小组有若干人,新年互送贺年卡一张,
已知全组共送贺年卡72张,则这个小组有( )
A.12人 B.18人 C.9人 D.10人
C
设这个小组有x人,
x(x-1)=72,
解之得 x1=9,x2=-8(舍).
四、及时巩固
∴x2-11x+30=0,
解之得 x1=5,x2=6.
当x=5时,则11-5=6,
当x=6时,则11-6=5.
∴能围成面积是30cm2的矩形.
2.有一根长22cm的铁丝:
(1)能否围成面积是30cm2的矩形?
解:设矩形一边长为xcm,则另一边长为(11-x)cm.
∴x(11-x)=30,
四、及时巩固
x
11-x
2.有一根长22cm的铁丝:
(2)能否围成面积是32cm2的矩形?并说明理由.
解:设矩形一边长为xcm,则另一边长为(11-x)cm.
∴x(11-x)=32,
∴x2-11x+32=0,
∵△=112-128=-7<0,
∴原方程无解.
∴不能围成面积是32cm2的矩形.
四、及时巩固
x
11-x
2.有一根长22cm的铁丝:
(3)能否求出所能围成的矩形面积的最大值.
解:设矩形一边长为xcm,则另一边长为(11-x)cm.
∴S矩形=x(11-x),
四、及时巩固
x
11-x
2.有一根长22cm的铁丝:
(3)能否求出所能围成的矩形面积的最大值.
解:设矩形一边长为xcm,则另一边长为(11-x)cm.
∴S矩形=x(11-x),
∴S矩形=-x2+11x
=-(x2-11x)
=-(x2-11x+ - )
=-(x- )2+ .
∴当x= 时,S矩形最大值= .
四、及时巩固
x
11-x
3.如图,把长为40cm,宽30cm的长方形硬纸板,
剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),将剩余的部分折成一个有盖的长方体盒子,设剪掉的小正方形边长为xcm(纸板的厚度忽略不计).
(1)长方体盒子的长、宽、高分别为多少cm.
解:(1) 高为x cm,
长为(30-2x)cm,
宽为(40-2x)÷2=(20-x)cm.
四、及时巩固
(2)若折成一个长方体盒子表面积是950cm2,
求此时长方体盒子的体积.
高为 x cm;
长为(30-2x)cm;
宽为 (20-x) cm.
(2) 由题意得
950+2(x2+20x)=30×40,
解之得 x1=5,x2=-25(舍),
∴V=(30-2×5)×5×(20-5)=1500(cm3).
答:长方体盒子的体积为1500cm3.
四、及时巩固
4.如图,在Rt△ABC中,∠B=90°,AB=5cm,
BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q两点同时出发.
(1)几秒后,△PBQ的面积等于4cm2?
四、及时巩固
2t
5-t
t
2t
5-t
t
解:(1)设时间为t,
AP=t,BP=5-t,BQ=2t,
∵∠B=90°,
∴S△PBQ= BP·BQ
= ·2t(5-t)=4,
整理,得 t2-5t+4=0,
4.如图,在Rt△ABC中,∠B=90°,AB=5cm,
BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q两点同时出发.
(1)几秒后,△PBQ的面积等于4cm2?
解之,得 t1=4,t2=1.
当t=4时,BQ=8>7,
不成立,舍去.
∴1秒后,△PBQ的面积等于4cm2.
四、及时巩固
2t
5-t
t
2t
5-t
t
4.如图,在Rt△ABC中,∠B=90°,AB=5cm,
BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q两点同时出发.
(2)几秒钟后,P、Q间的距离等于5cm?
四、及时巩固
(2)设时间为t,
在Rt△PBQ中,PQ2=BQ2+BP2,
∴52=(2t)2+(5-t)2,
解之,得 t1=0(舍去),t2=2.
∴2秒后,P、Q的距离等于5cm.
2t
5-t
t
五、总结反思
实际问题
数学问题
(方程)
方程的解
列一元二次方程
解方程
解释、检验
一元二次方程
复习(1)
一元二次方程应用的一般步骤:
1.审(题);
2.找(数量关系);
3.设(未知数);
4.列(出方程);
5.解(方程);
6.检(验根的合理性);
7.答(写出答案).
一、复习回顾
1.一件商品的原价是100元,经过两次提价后的
价格为121元,如果每次提价的百分率都是x,根据题意,下面列出的方程正确的是( )
A.100(1+x)=121; B.100(1-x)=121;
C.100(1+x)2=121; D.100(1-x)2=121.
C
二、尝试解决
若平均增长(或降低)百分率都是x,
增长(或降低)前的量是a,
增长(或降低)n次后的量是b,
则他们的数量关系可表示为a(1±x)n=b.
二、尝试解决
2.如图,某中学准备在校园里利用围墙的一段,
再砌三面墙,围成一个矩形花园ABCD( 围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2.
二、尝试解决
解:设AB的长为x m,
则BC=(50-2x)m,
x(50-2x)=300,
解得x1=10,x2=15.
注意围墙的长度
当x=10时,BC=30>25,
∴不符合题意,舍去.
∴当x=15m,BC=20m时,矩形花园的面积为300m2.
二、尝试解决
x
50-2x
3.某单位准备将院内一块长30 m,宽20 m的长方形
空地,建成一个矩形花园.要求在花园中修两条纵向
平行和一条横向弯折的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为532 m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)
二、尝试解决
解:设小道进出口的宽度
为x米,依题意得
(30-2x)(20-x)=532,
整理,得x2-35x+34=0,
解之,得 x1=1,x2=34.
∵34>30,
∴x=1.
答:小道进出口的宽度应为1米.
30-2x
20-x
平移法
二、尝试解决
例1.李老伯在该土地上种植西瓜,喜获丰收,
经计算西瓜成本2元/千克,若以3元/千克的
价格出售,每天可售出200千克,为了促销,李老伯决定降价销售.经调查发现,这种西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本需要24元.李老伯要想每天盈利200元,并想使西瓜尽快销售出去,应将每千克西瓜的售价降低多少钱?
设每千克西瓜降低x元;
总利润=(售价-进价)×销量-固定成本
三、例题解析
单价 成本 销量 固定成本
降价前 3 2 200 24
降价后 2 24
3-x
200+400x
解:设每千克西瓜降低x元,
(3-x-2)(200+400x)-24=200,
解之,得 x1=0.2,x2=0.3.
∵为使西瓜尽快销售出去,
∴x=0.3.
答:每千克西瓜的售价降低0.3元.
三、例题解析
例1.李老伯在该土地上种植西瓜,喜获丰收,
经计算西瓜成本2元/千克,若以3元/千克的
价格出售,每天可售出200千克,为了促销,李老伯决定降价销售.经调查发现,这种西瓜每降价0.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本需要24元.李老伯要想每天盈利200元,并想使西瓜尽快销售出去,应将每千克西瓜的售价降低多少钱?
例如,在绿地中间开辟一个矩形的花圃,使四周的绿地等宽,绿地的面积与花圃的面积相等,你能计算出剩余绿地的宽吗?
例2:在一块长是32m、宽24m的矩形绿地内,要围
出一个花圃,使花圃面积是矩形面积的一半,你能给出设计方案吗?
三、例题解析
例如,在绿地中间开辟一个矩形的花圃,使四周的绿地等宽,绿地的面积与花圃的面积相等,你能计算出剩余绿地的宽吗?
例2:在一块长是32m、宽24m的矩形绿地内,要围
出一个花圃,使花圃面积是矩形面积的一半,你能给出设计方案吗?
x
解:设剩余绿地的等宽长为xm,
x
三、例题解析
32
24
例如,在绿地中间开辟一个矩形的花圃,使四周的绿地等宽,绿地的面积与花圃的面积相等,你能计算出剩余绿地的宽吗?
例2:在一块长是32m、宽24m的矩形绿地内,要围
出一个花圃,使花圃面积是矩形面积的一半,你能给出设计方案吗?
(32-2x)(24-2x)=×32×24,
解得,x1=4,x2=24(舍).
答:绿地的宽为4m.
x
解:设剩余绿地的等宽长为xm,
x
三、例题解析
32
24
例3.如图,在矩形中ABCD,AB=6cm,BC=12cm,
点P从点A出发沿AB以1cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2cm/s的速度向点C移动.
(1)几秒钟后△DPQ的面积等于31cm2;
x
2x
6-x
12-2x
三、例题解析
解:设x秒后△DPQ的
面积为31cm2,
则AP=xcm,BP=(6-x)cm,
BQ=2xcm,CQ=(12-2x)cm,
由题意得:
6×12-0.5×12x-0.5×6(12-2x)
-0.5(6-x)2x=31,
整理,得x2-6x+8=0,
解之得 x1=1,x2=5.
答:1s或5s后△DPQ的面积为31cm2.
三、例题解析
x
2x
6-x
12-2x
解:设x秒后△DPQ的
面积为31cm2,
则AP=xcm,BP=(6-x)cm,
BQ=2xcm,CQ=(12-2x)cm,
由题意得:
0.5×12x+0.5×6(12-2x)+0.5(6-x)2x=41,
解之得 x1=1,x2=5.
答:1s或5s后△DPQ的面积为31cm2.
九年级数学名师课程
三、例题解析
x
2x
6-x
12-2x
三、例题解析
例3.(2)在运动过程中,是否存在这样的时刻,
使以点QP=QD.若存在,求出运动时间;若不存在,请说明理由.
x
2x
6-x
12-2x
假设运动开始后第x秒时,满足QP=QD,
∵QP2=PB2+BQ2=(6-x)2+(2x)2,
QD2=QC2+CD2=(12-2x)+62,
∴(12-2x)2+62=(6-x)2+(2x)2,
∴ x2+36x-144=0,
∴ x1=-18+6 ,x2=-18-6.
∵0<-18+6<6 ,∴x=-18+6.
三、例题解析
例3.(2)在运动过程中,是否存在这样的时刻,
使以点QP=QD.若存在,求出运动时间;若不存在,请说明理由.
x
2x
6-x
12-2x
1.一个小组有若干人,新年互送贺年卡一张,
已知全组共送贺年卡72张,则这个小组有( )
A.12人 B.18人 C.9人 D.10人
C
设这个小组有x人,
x(x-1)=72,
解之得 x1=9,x2=-8(舍).
四、及时巩固
∴x2-11x+30=0,
解之得 x1=5,x2=6.
当x=5时,则11-5=6,
当x=6时,则11-6=5.
∴能围成面积是30cm2的矩形.
2.有一根长22cm的铁丝:
(1)能否围成面积是30cm2的矩形?
解:设矩形一边长为xcm,则另一边长为(11-x)cm.
∴x(11-x)=30,
四、及时巩固
x
11-x
2.有一根长22cm的铁丝:
(2)能否围成面积是32cm2的矩形?并说明理由.
解:设矩形一边长为xcm,则另一边长为(11-x)cm.
∴x(11-x)=32,
∴x2-11x+32=0,
∵△=112-128=-7<0,
∴原方程无解.
∴不能围成面积是32cm2的矩形.
四、及时巩固
x
11-x
2.有一根长22cm的铁丝:
(3)能否求出所能围成的矩形面积的最大值.
解:设矩形一边长为xcm,则另一边长为(11-x)cm.
∴S矩形=x(11-x),
四、及时巩固
x
11-x
2.有一根长22cm的铁丝:
(3)能否求出所能围成的矩形面积的最大值.
解:设矩形一边长为xcm,则另一边长为(11-x)cm.
∴S矩形=x(11-x),
∴S矩形=-x2+11x
=-(x2-11x)
=-(x2-11x+ - )
=-(x- )2+ .
∴当x= 时,S矩形最大值= .
四、及时巩固
x
11-x
3.如图,把长为40cm,宽30cm的长方形硬纸板,
剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),将剩余的部分折成一个有盖的长方体盒子,设剪掉的小正方形边长为xcm(纸板的厚度忽略不计).
(1)长方体盒子的长、宽、高分别为多少cm.
解:(1) 高为x cm,
长为(30-2x)cm,
宽为(40-2x)÷2=(20-x)cm.
四、及时巩固
(2)若折成一个长方体盒子表面积是950cm2,
求此时长方体盒子的体积.
高为 x cm;
长为(30-2x)cm;
宽为 (20-x) cm.
(2) 由题意得
950+2(x2+20x)=30×40,
解之得 x1=5,x2=-25(舍),
∴V=(30-2×5)×5×(20-5)=1500(cm3).
答:长方体盒子的体积为1500cm3.
四、及时巩固
4.如图,在Rt△ABC中,∠B=90°,AB=5cm,
BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q两点同时出发.
(1)几秒后,△PBQ的面积等于4cm2?
四、及时巩固
2t
5-t
t
2t
5-t
t
解:(1)设时间为t,
AP=t,BP=5-t,BQ=2t,
∵∠B=90°,
∴S△PBQ= BP·BQ
= ·2t(5-t)=4,
整理,得 t2-5t+4=0,
4.如图,在Rt△ABC中,∠B=90°,AB=5cm,
BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q两点同时出发.
(1)几秒后,△PBQ的面积等于4cm2?
解之,得 t1=4,t2=1.
当t=4时,BQ=8>7,
不成立,舍去.
∴1秒后,△PBQ的面积等于4cm2.
四、及时巩固
2t
5-t
t
2t
5-t
t
4.如图,在Rt△ABC中,∠B=90°,AB=5cm,
BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P、Q两点同时出发.
(2)几秒钟后,P、Q间的距离等于5cm?
四、及时巩固
(2)设时间为t,
在Rt△PBQ中,PQ2=BQ2+BP2,
∴52=(2t)2+(5-t)2,
解之,得 t1=0(舍去),t2=2.
∴2秒后,P、Q的距离等于5cm.
2t
5-t
t
五、总结反思
实际问题
数学问题
(方程)
方程的解
列一元二次方程
解方程
解释、检验
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
