人教版九年级上册25概率初步复习课件(共34张PPT)
文档属性
| 名称 | 人教版九年级上册25概率初步复习课件(共34张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 478.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 17:51:13 | ||
图片预览










文档简介
(共34张PPT)
概率初步单元复习
学习目标:
1.理解随机事件的定义及概率的定义;
2.能够用列举法计算简单事件的发生概率,能够通过重复试验,用事件发生的频率估计概率;
3.通过实例进一步丰富对概率的认识,并能解决一些简单的实际问题.
学习重点:
复习概率的重点知识,构建本章知识结构.
同学们,通过对本章的学习,你对本章的知识结构和重要知识点及其运用是否有一个清晰的认识呢?
让我们带着下列问题,一起进行梳理总结.
知识梳理
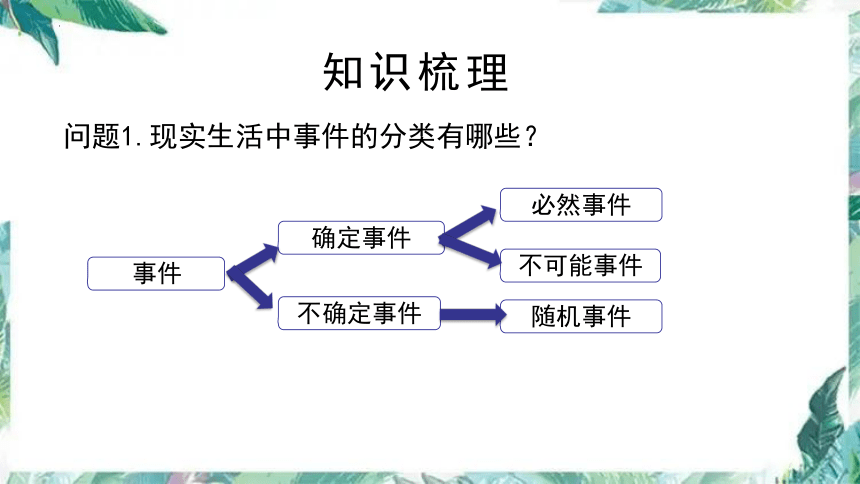
问题1.现实生活中事件的分类有哪些?
事件
确定事件
不确定事件
必然事件
不可能事件
随机事件
问题2.回顾课本的练习,以下分别属于什么类型的事件?
(1)通常加热到100℃时,水沸腾;
(2)掷一枚硬币,正面向上;
(3)篮球队员投篮一次,投中;
(4)任意画一个三角形,其内角和是360°;
必然事件
随机事件
随机事件
不可能事件
问题3.随机事件(2)、(3)发生的可能性大小能否确定?
(1)通常加热到100℃时,水沸腾;
(2)掷一枚硬币,正面向上;
(3)篮球队员投篮一次,投中;
(4)任意画一个三角形,其内角和是360°;
必然事件
随机事件
随机事件
不可能事件
我们可以通过抛掷硬币的试验或者投篮的试验,
对随机性的结果进行统计,可以找出规律性.
通过规律性来确定随机事件发生的可能性大小.
问题4.用什么来刻画随机事件发生的可能性大小?
概率表示事件发生的可能性大小,事件发生的可能性越大,它的概率越接近于1,反之事件发生的可能性越小,则它的概率越接近于0.
概率
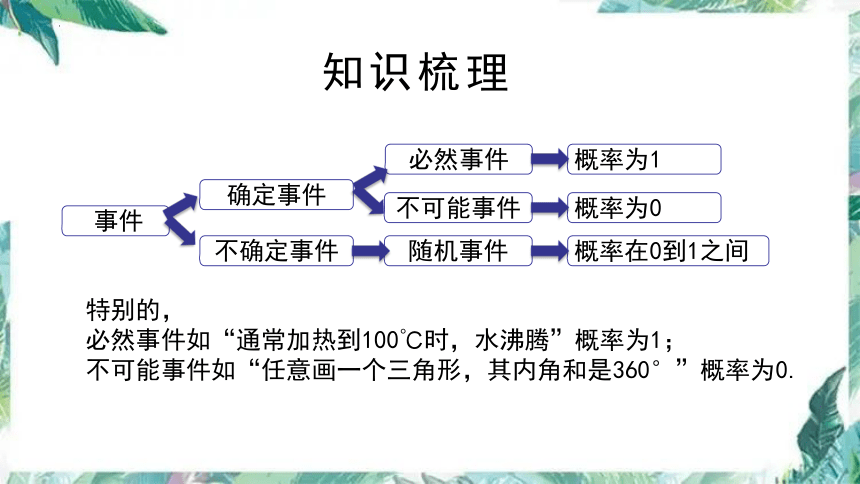
知识梳理
事件
确定事件
不确定事件
必然事件
不可能事件
随机事件
概率在0到1之间
概率为1
概率为0
特别的,
必然事件如“通常加热到100℃时,水沸腾”概率为1;
不可能事件如“任意画一个三角形,其内角和是360°”概率为0.
问题5.如何求随机事件的概率呢?
(2)掷一枚硬币,正面向上;
(3)篮球队员投篮一次,投中;
思考1.掷一枚硬币,正面向上的概率为多少?
思考2.运动员投篮一次,投中的概率约为多少?
思考1. 掷一枚硬币,正面向上的概率为多少?
解:掷一枚硬币,向上的结果有2种等可能的情况,分别为正面向上和反面向上.
P(正面向上)=
在什么条件下,可以通过列举法得到随机事件的概率?
列举法
结果为有限个
各种结果出现的可能性相等
变式 向空中抛掷两枚质地均匀的硬币,可否用列举法求两枚硬币全部正面向上的概率?
解:将两枚硬币分别记作 A、B,于是可以直接枚举得到:
(A正,B正)(A正,B反)(A反,B正)(A反,B反)
4种等可能的结果,两枚正面向上的有1种..
P(两枚正面向上)=
方法一
解:两枚硬币分别记为第 1 枚和第 2 枚,可以用列表法表示出所有可能出现的结果.
由此表可以看出,同时抛掷两枚硬币,可能出现的结果有 4 个,并且它们出现的可能性相等,两枚正面向上的有1种.
正 反
正 (正,正) (反,正)
反 (正,反) (反,反)
第 1 枚
第 2 枚
P(两枚正面向上)= .
方法二
解:两枚硬币分别记为第1枚、第2枚,可以画出如下树状图
第1枚 正 反
正 反
正 反
由树状图可以看出,所有可能出现的结果共有4种,这些结果的可能性相等,两枚正面向上的有1种.
第2枚
方法三
P(两枚正面向上)= .
√
变式 向空中抛掷三枚质地均匀的硬币,三枚硬币全部正面向上的概率呢?
枚举法
列表法
树状图法
√
解:三枚硬币分别记为第1枚、第2枚、第3枚,可以画出如下树状图:
第1枚 正 反
第3枚
正 反
正 反
正 反
正 反
正 反
正 反
由树状图可以看出,所有可能出现的结果共有12种,这些结果的可能性相等,三枚正面向上的有1种.
P(三枚正面向上)=
第2枚
√
知识梳理
用列举法求概率有哪些具体的方法?它们各有什么特点?
事件
确定事件
不确定事件
必然事件
不可能事件
随机事件
概率
(可能性大小)
列举法求概率
枚举法
列表法
(两步)
树状图法
(两步及两步以上)
思考2.运动员投篮一次,投中的概率约为多少?
分析:能否用列举法求出概率
出现“投中”和“没投中”两种情况.
(2)每种结果的可能性相等吗
无法判断“结果是否具有等可能性”,
故我们无法用列举法求出概率.
用频率估计概率
(1)运动员投篮一次,结果有哪些情况?
第一步:记录某运动员在罚球线上投篮的结果.
投篮次数n 50 100 150 200 250 300
投中次数m 28 60 78 104 123 152
投中频率
第二步:计算投中的频率(结果保留小数点后两位);第三步:估算这名运动员投篮一次,投中的概率约为多少(结果保留小数点后一位).
0.56
0.60
0.52
0.52
0.49
0.51
P(投中)≈ 0.5
知识梳理
事件
确定事件
不确定事件
必然事件
不可能事件
随机事件
概率
列举法求概率
枚举法
列表法
(两步)
树状图法
(两步及两步以上)
利用频率估计概率
(1)事件的分类有哪些.
(2)在什么条件下,可以通过列举法得到随机事件的概率.
(3)用列举法求概率有哪些具体的方法,它们各有什么特点.
(4)如何用频率估计概率.
课堂小结
用概率解决实际问题
例题精讲
例1.下列事件是必然事件的是( )
A.任意一个五边形的外角和等于540°.
B.掷一枚硬币,有国徽的一面朝下.
C.3个人分成两组,一定有2个人分在一组.
D.打开电视,正在播放动画片.
C
例2.从1,2,3,4,5,6,7,8,9,10这十个数字中随机取出一个数,取出的数能被3整除的概率是 .
例题精讲
解:抽取的数有10种可能,即1,2,3,4,5,6,7,8,9,10,在这十个数中只有3,6,9能被3整除,所以
枚举法:当事件涉及的对象比较单一且出现的等可能结果数目较少时.
P(能被3整除)=
例3.如图所示是四张质地相同的卡片.将卡片洗匀后,背面朝上放置在桌面上.
小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?请用列表法或画树状图法说明理由.
2
2
3
6
游戏规则
随机抽取一张卡片,记下数字放回,洗匀后再抽一张.将抽取的第一张、第二张卡片上的数字分别作为十位数字和个位数字,若组成的两位数不超过 32,则小贝胜,反之小晶胜.
例题精讲
解:可以用列表法表示出所有可能出现的结果.
由此表可以看出,组成的两位数,可能出现的结果有16个,并且它们出现的可能性相等,组成的两位数不超过32的有10个.
P(小贝胜)= P(小晶胜)=
概率不相等,游戏不公平.
2 2 3 6
2 (2,2) (2,2) (2,3) (2,6)
2 (2,2) (2,2) (2,3) (2,6)
3 (3,2) (3,2) (3,3) (3,6)
6 (6,2) (6,2) (6,3) (6,6)
第 1 张
第 2 张
列表法:当一次试验涉及两个因素并且可能出现的结果数目较多时.
解:可以画出如下树状图:
第1张 2 2 3 6
第2张
2 2 3 6
由树状图可以看出,所有可能出现的结果共有16种,这些结果的可能性相等,组成的两位数不超过32的有10个.
2 2 3 6
2 2 3 6
2 2 3 6
两位数 22 22 23 26 22 22 23 26 32 32 33 36 62 62 63 66
P(小贝胜)= P(小晶胜)=
概率不相等,游戏不公平.
√
√
√
√
√
√
√
√
√
√
画树状图法:当一次试验涉及两个或更多个因素.
例4. 在一个不透明的布袋中装有红色、白色玻璃球共 40 个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在0.15左右,则口袋中红色球可能有( ).
A.4个 B.6个 C.34个 D.36个
B
分析:随着试验次数的增加,摸到红球的频率稳定在0.15左右.
可以用频率估计概率,得到摸到红球的概率为0.15.
40×0.15=6(个)
易错点分析1
在叙述必然事件、不可能事件和随机事件时,为什么反复提到“在一定条件下”,这是因为必然事件、不可能事件和随机事件都会受到外在条件的制约.
例如1:标准大气压下,水加热到100℃沸腾是必然事件,
但是气压高于标准大气压时,水加热到100℃沸腾就不是必然事件了.
易错点分析2
概率是针对大量重复试验而言的,大量重复试验反映的规律并非在每一次试验中都发生.
例如2:如果某一彩票的中奖概率是 ,那么买1000张彩票就一定能中奖,这种说法对吗?
不正确,购彩票中奖属于随机事件,结果是不确定的.
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率为
易错点分析3
在使用公式求概率时,全面列举出所有等可能的结果和所关注的结果,各种情况不能遗漏,也不能重复.
例如3: 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,摸出白球和摸出红球的可能性是否相同
解:
摸出的球不是白球就是红球,故摸出白球和摸出红球的可能性相同.
例如3: 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,摸出白球和摸出红球的可能性是否相同
白
红1
红2
解:由于袋中有2个红球可以将它们编号后再求解,所有可能出现的结果共有3种,这些结果的可能性相等,摸出红球的情况数有2种.
故摸出一个球是红球的概率为三分之二,摸出一个球是白球的概率则为三分之一,摸出白球和摸出红球可能性不同.
“不能遗漏”
例如4:一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出两个球,问:两次都摸出红球的概率是多少
白 红1 红2
白 (白,白) (红1,白) (红2,白)
红1 (白,红1) (红1,红1) (红2,红1)
红2 (白,红2) (红1,红2) (红2,红2)
解:记“两次都摸出红球”为事件A,列表如下:
“不放回”
例如4:一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出两个球,问:两次都摸出红球的概率是多少
白 红1 红2
白 (红1,白) (红2,白)
红1 (白,红1) (红2,红1)
红2 (白,红2) (红1,红2)
“不能重复”
解:记“两次都摸出红球”为事件A,列表如下:
谢谢
概率初步单元复习
学习目标:
1.理解随机事件的定义及概率的定义;
2.能够用列举法计算简单事件的发生概率,能够通过重复试验,用事件发生的频率估计概率;
3.通过实例进一步丰富对概率的认识,并能解决一些简单的实际问题.
学习重点:
复习概率的重点知识,构建本章知识结构.
同学们,通过对本章的学习,你对本章的知识结构和重要知识点及其运用是否有一个清晰的认识呢?
让我们带着下列问题,一起进行梳理总结.
知识梳理
问题1.现实生活中事件的分类有哪些?
事件
确定事件
不确定事件
必然事件
不可能事件
随机事件
问题2.回顾课本的练习,以下分别属于什么类型的事件?
(1)通常加热到100℃时,水沸腾;
(2)掷一枚硬币,正面向上;
(3)篮球队员投篮一次,投中;
(4)任意画一个三角形,其内角和是360°;
必然事件
随机事件
随机事件
不可能事件
问题3.随机事件(2)、(3)发生的可能性大小能否确定?
(1)通常加热到100℃时,水沸腾;
(2)掷一枚硬币,正面向上;
(3)篮球队员投篮一次,投中;
(4)任意画一个三角形,其内角和是360°;
必然事件
随机事件
随机事件
不可能事件
我们可以通过抛掷硬币的试验或者投篮的试验,
对随机性的结果进行统计,可以找出规律性.
通过规律性来确定随机事件发生的可能性大小.
问题4.用什么来刻画随机事件发生的可能性大小?
概率表示事件发生的可能性大小,事件发生的可能性越大,它的概率越接近于1,反之事件发生的可能性越小,则它的概率越接近于0.
概率
知识梳理
事件
确定事件
不确定事件
必然事件
不可能事件
随机事件
概率在0到1之间
概率为1
概率为0
特别的,
必然事件如“通常加热到100℃时,水沸腾”概率为1;
不可能事件如“任意画一个三角形,其内角和是360°”概率为0.
问题5.如何求随机事件的概率呢?
(2)掷一枚硬币,正面向上;
(3)篮球队员投篮一次,投中;
思考1.掷一枚硬币,正面向上的概率为多少?
思考2.运动员投篮一次,投中的概率约为多少?
思考1. 掷一枚硬币,正面向上的概率为多少?
解:掷一枚硬币,向上的结果有2种等可能的情况,分别为正面向上和反面向上.
P(正面向上)=
在什么条件下,可以通过列举法得到随机事件的概率?
列举法
结果为有限个
各种结果出现的可能性相等
变式 向空中抛掷两枚质地均匀的硬币,可否用列举法求两枚硬币全部正面向上的概率?
解:将两枚硬币分别记作 A、B,于是可以直接枚举得到:
(A正,B正)(A正,B反)(A反,B正)(A反,B反)
4种等可能的结果,两枚正面向上的有1种..
P(两枚正面向上)=
方法一
解:两枚硬币分别记为第 1 枚和第 2 枚,可以用列表法表示出所有可能出现的结果.
由此表可以看出,同时抛掷两枚硬币,可能出现的结果有 4 个,并且它们出现的可能性相等,两枚正面向上的有1种.
正 反
正 (正,正) (反,正)
反 (正,反) (反,反)
第 1 枚
第 2 枚
P(两枚正面向上)= .
方法二
解:两枚硬币分别记为第1枚、第2枚,可以画出如下树状图
第1枚 正 反
正 反
正 反
由树状图可以看出,所有可能出现的结果共有4种,这些结果的可能性相等,两枚正面向上的有1种.
第2枚
方法三
P(两枚正面向上)= .
√
变式 向空中抛掷三枚质地均匀的硬币,三枚硬币全部正面向上的概率呢?
枚举法
列表法
树状图法
√
解:三枚硬币分别记为第1枚、第2枚、第3枚,可以画出如下树状图:
第1枚 正 反
第3枚
正 反
正 反
正 反
正 反
正 反
正 反
由树状图可以看出,所有可能出现的结果共有12种,这些结果的可能性相等,三枚正面向上的有1种.
P(三枚正面向上)=
第2枚
√
知识梳理
用列举法求概率有哪些具体的方法?它们各有什么特点?
事件
确定事件
不确定事件
必然事件
不可能事件
随机事件
概率
(可能性大小)
列举法求概率
枚举法
列表法
(两步)
树状图法
(两步及两步以上)
思考2.运动员投篮一次,投中的概率约为多少?
分析:能否用列举法求出概率
出现“投中”和“没投中”两种情况.
(2)每种结果的可能性相等吗
无法判断“结果是否具有等可能性”,
故我们无法用列举法求出概率.
用频率估计概率
(1)运动员投篮一次,结果有哪些情况?
第一步:记录某运动员在罚球线上投篮的结果.
投篮次数n 50 100 150 200 250 300
投中次数m 28 60 78 104 123 152
投中频率
第二步:计算投中的频率(结果保留小数点后两位);第三步:估算这名运动员投篮一次,投中的概率约为多少(结果保留小数点后一位).
0.56
0.60
0.52
0.52
0.49
0.51
P(投中)≈ 0.5
知识梳理
事件
确定事件
不确定事件
必然事件
不可能事件
随机事件
概率
列举法求概率
枚举法
列表法
(两步)
树状图法
(两步及两步以上)
利用频率估计概率
(1)事件的分类有哪些.
(2)在什么条件下,可以通过列举法得到随机事件的概率.
(3)用列举法求概率有哪些具体的方法,它们各有什么特点.
(4)如何用频率估计概率.
课堂小结
用概率解决实际问题
例题精讲
例1.下列事件是必然事件的是( )
A.任意一个五边形的外角和等于540°.
B.掷一枚硬币,有国徽的一面朝下.
C.3个人分成两组,一定有2个人分在一组.
D.打开电视,正在播放动画片.
C
例2.从1,2,3,4,5,6,7,8,9,10这十个数字中随机取出一个数,取出的数能被3整除的概率是 .
例题精讲
解:抽取的数有10种可能,即1,2,3,4,5,6,7,8,9,10,在这十个数中只有3,6,9能被3整除,所以
枚举法:当事件涉及的对象比较单一且出现的等可能结果数目较少时.
P(能被3整除)=
例3.如图所示是四张质地相同的卡片.将卡片洗匀后,背面朝上放置在桌面上.
小贝和小晶想用以上四张卡片做游戏,游戏规则见信息图.你认为这个游戏公平吗?请用列表法或画树状图法说明理由.
2
2
3
6
游戏规则
随机抽取一张卡片,记下数字放回,洗匀后再抽一张.将抽取的第一张、第二张卡片上的数字分别作为十位数字和个位数字,若组成的两位数不超过 32,则小贝胜,反之小晶胜.
例题精讲
解:可以用列表法表示出所有可能出现的结果.
由此表可以看出,组成的两位数,可能出现的结果有16个,并且它们出现的可能性相等,组成的两位数不超过32的有10个.
P(小贝胜)= P(小晶胜)=
概率不相等,游戏不公平.
2 2 3 6
2 (2,2) (2,2) (2,3) (2,6)
2 (2,2) (2,2) (2,3) (2,6)
3 (3,2) (3,2) (3,3) (3,6)
6 (6,2) (6,2) (6,3) (6,6)
第 1 张
第 2 张
列表法:当一次试验涉及两个因素并且可能出现的结果数目较多时.
解:可以画出如下树状图:
第1张 2 2 3 6
第2张
2 2 3 6
由树状图可以看出,所有可能出现的结果共有16种,这些结果的可能性相等,组成的两位数不超过32的有10个.
2 2 3 6
2 2 3 6
2 2 3 6
两位数 22 22 23 26 22 22 23 26 32 32 33 36 62 62 63 66
P(小贝胜)= P(小晶胜)=
概率不相等,游戏不公平.
√
√
√
√
√
√
√
√
√
√
画树状图法:当一次试验涉及两个或更多个因素.
例4. 在一个不透明的布袋中装有红色、白色玻璃球共 40 个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在0.15左右,则口袋中红色球可能有( ).
A.4个 B.6个 C.34个 D.36个
B
分析:随着试验次数的增加,摸到红球的频率稳定在0.15左右.
可以用频率估计概率,得到摸到红球的概率为0.15.
40×0.15=6(个)
易错点分析1
在叙述必然事件、不可能事件和随机事件时,为什么反复提到“在一定条件下”,这是因为必然事件、不可能事件和随机事件都会受到外在条件的制约.
例如1:标准大气压下,水加热到100℃沸腾是必然事件,
但是气压高于标准大气压时,水加热到100℃沸腾就不是必然事件了.
易错点分析2
概率是针对大量重复试验而言的,大量重复试验反映的规律并非在每一次试验中都发生.
例如2:如果某一彩票的中奖概率是 ,那么买1000张彩票就一定能中奖,这种说法对吗?
不正确,购彩票中奖属于随机事件,结果是不确定的.
一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m种结果,那么事件A发生的概率为
易错点分析3
在使用公式求概率时,全面列举出所有等可能的结果和所关注的结果,各种情况不能遗漏,也不能重复.
例如3: 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,摸出白球和摸出红球的可能性是否相同
解:
摸出的球不是白球就是红球,故摸出白球和摸出红球的可能性相同.
例如3: 一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,摸出白球和摸出红球的可能性是否相同
白
红1
红2
解:由于袋中有2个红球可以将它们编号后再求解,所有可能出现的结果共有3种,这些结果的可能性相等,摸出红球的情况数有2种.
故摸出一个球是红球的概率为三分之二,摸出一个球是白球的概率则为三分之一,摸出白球和摸出红球可能性不同.
“不能遗漏”
例如4:一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出两个球,问:两次都摸出红球的概率是多少
白 红1 红2
白 (白,白) (红1,白) (红2,白)
红1 (白,红1) (红1,红1) (红2,红1)
红2 (白,红2) (红1,红2) (红2,红2)
解:记“两次都摸出红球”为事件A,列表如下:
“不放回”
例如4:一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出两个球,问:两次都摸出红球的概率是多少
白 红1 红2
白 (红1,白) (红2,白)
红1 (白,红1) (红2,红1)
红2 (白,红2) (红1,红2)
“不能重复”
解:记“两次都摸出红球”为事件A,列表如下:
谢谢
同课章节目录
