人教A版2019选择性必修第三册 专题强化二 概率与统计的综合应用 学案(Word版含答案)
文档属性
| 名称 | 人教A版2019选择性必修第三册 专题强化二 概率与统计的综合应用 学案(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 11:14:51 | ||
图片预览



文档简介
专题强化二 概率与统计的综合应用
概率与统计内容在考试考查中逐步呈现出综合性、应用性和创新性等特点,该题目的设置常常以社会、经济、科技发展为背景,以考生比较熟悉的实际应用问题为载体,考查学生统计图表的识别,应用基础知识和基本方法分析问题和解决问题的能力,充分体现了概率与统计的工具性和交汇性.
统计图表与正态分布
1.为建立健全国家学生体质健康监测评价机制,激励学生积极参加身体锻炼,教育部印发《国家学生体质健康标准(2014年修订)》(简称《标准》),要求各学校每学年开展覆盖本校各年级学生的《标准》测试工作,并依据学生学年总分评定等级.某市在高三年级开展了一次体质健康模拟测试(满分100分),从中随机抽取了200名学生的测试成绩,并据此绘制了如图所示的频率分布直方图.
(1)估计这200名学生测试成绩的平均数和方差(同一组数据用该组区间的中点值作代表).
(2)由频率分布直方图知,该市高三学生的健康指数服从正态分布,其中近似为样本平均数,近似为样本方差.
①求;
②已知该市高三学生约有10000名,记测试成绩在区间的人数为,求.
附:参考数据.若随机变量服从正态分布,则,,.
统计图表与统计分析
2.2022年2月1日是春节,百节年为首,春节是中华民族最隆重的传统佳节,它不仅集中体现了中华民族的思想信仰、理想愿望、生活娱乐和文化心理,而且还是祈福攮灾、饮食和娛乐活动的狂欢式展示.为调查某地从外地工作回来过年的市民(以下称为“返赣人员”)人数情况,现对某一区域的居民进行抽样调查,并按年龄(单位:岁)分成五组,得到如图所示的频率分布直方图,其中年龄在内的人数为10.
(1)请根据样本数据补充完成列联表,并判断是否有99.9%的把握认为是否是从外地回来过年与性别相关;
返赣人员 本地人员 合计
男 15
女 10 40
合计
(2)据了解,该地区今年返赣人员占.现从该社区居民中随机抽取3人进行调查,记X为这3人中今年是返赣人员的人数,求X的分布列与数学期望.
参考公式:,其中.参考数据:
0.10 0.05 0.010 0.001
2.706 3.841 6.635 10.828
三、概率统计中的决策问题
3.某冰糖橙是甜橙的一种,以味甜皮薄著称.该橙按照等级可分为四类:珍品、特级、优级和一级.某采购商打算订购一批橙子销往省外,并从采购的这批橙子中随机抽取100箱(每箱有5kg),利用橙子的等级分类标准得到的数据如下表:
等级 珍品 特级 优级 一级
箱数 40 30 10 20
(1)若将频率作为概率,从这100箱橙子中有放回地随机抽取4箱,求恰好有2箱是一级品的概率;
(2)利用样本估计总体,果园老板提出两种方案供采购商参考:方案一:不分等级出售,价格为27元/kg;方案二:分等级出售,橙子价格如下表.
等级 珍品 特级 优级 一级
价格/(元∕kg) 36 30 24 18
从采购商的角度考虑,应该采用哪种方案?
(3)用分层随机抽样的方法从这100箱橙子中抽取10箱,再从抽取的10箱中随机抽取3箱,X表示抽取的珍品的箱数,求X的分布列及均值.
四、概率统计中的最值问题
4.在中国共产党的正确领导下,我国顺利实现了第一个百年奋斗目标——全面建成小康社会.某地为了巩固扶贫成果,决定继续对甲、乙两家乡镇企业进行指导.指导方式有两种,一种是精准指导,一种是综合指导.已知对甲企业采用精准指导时,投资50万元,增加100万元收入的概率为0.2,增加200万元收入的概率为0.8,采用综合指导时,投资100万元,增加200万元收入的概率为0.6,增加400万收入的概率为0.4;对乙企业采用精准指导时,投资50万元,增加100万元收入的概率为0.3,增加200万元收入的概率为0.7,采用综合指导时,投资100万元,增加200万元收入的概率为0.7,增加400万元收入的概率为0.3.指导结果在两家企业之间互不影响.
(1)若决策部门对甲企业进行精准指导、对乙企业进行综合指导,设两家企业增加的总收入为万元,求的分布列;
(2)若有150万元无息贷款可供甲、乙两家企业使用,对两家企业应分别进行哪种指导总收入最高?请说明理由.
【过关训练】
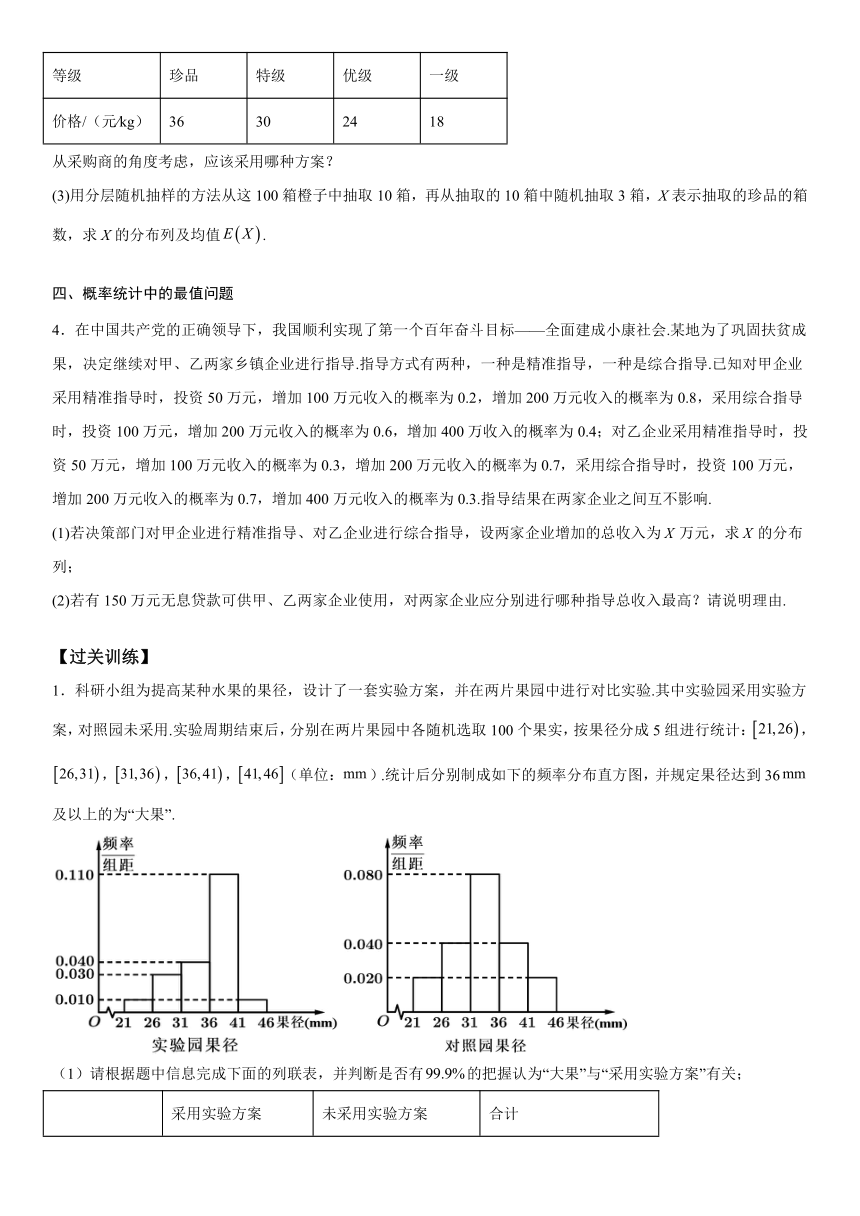
1.科研小组为提高某种水果的果径,设计了一套实验方案,并在两片果园中进行对比实验.其中实验园采用实验方案,对照园未采用.实验周期结束后,分别在两片果园中各随机选取100个果实,按果径分成5组进行统计:,,,,(单位:).统计后分别制成如下的频率分布直方图,并规定果径达到36及以上的为“大果”.
(1)请根据题中信息完成下面的列联表,并判断是否有的把握认为“大果”与“采用实验方案”有关;
采用实验方案 未采用实验方案 合计
大果
非大果
合计 100 100 200
(2)根据长期种植经验,可以认为对照园中的果径服从正态分布,其中近似为样本平均数,,请估计对照园中果径落在区间内的概率.(同一组中的数据以这组数据所在区间中点的值作代表)
附:①;
②若服从正态分布,则,,.
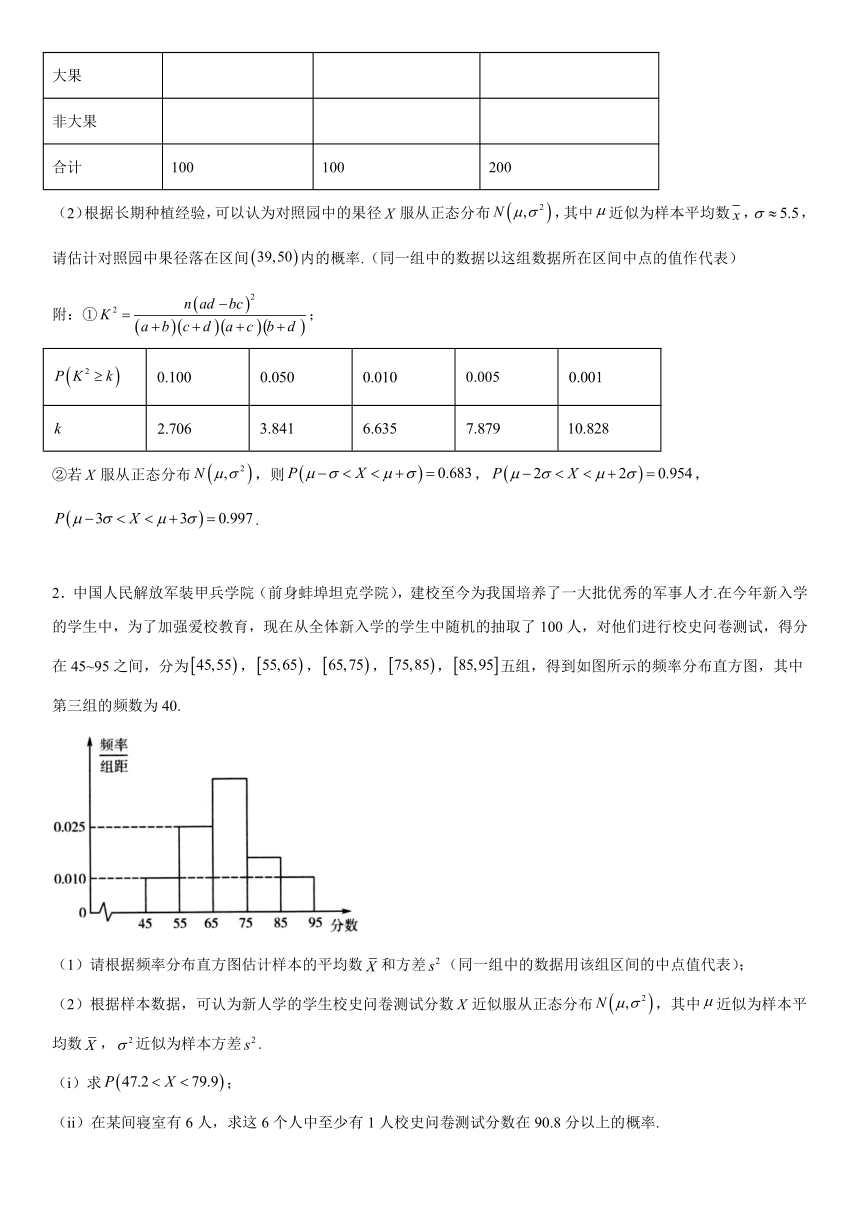
2.中国人民解放军装甲兵学院(前身蚌埠坦克学院),建校至今为我国培养了一大批优秀的军事人才.在今年新入学的学生中,为了加强爱校教育,现在从全体新入学的学生中随机的抽取了100人,对他们进行校史问卷测试,得分在45~95之间,分为,,,,五组,得到如图所示的频率分布直方图,其中第三组的频数为40.
(1)请根据频率分布直方图估计样本的平均数和方差(同一组中的数据用该组区间的中点值代表);
(2)根据样本数据,可认为新人学的学生校史问卷测试分数近似服从正态分布,其中近似为样本平均数,近似为样本方差.
(i)求;
(ii)在某间寝室有6人,求这6个人中至少有1人校史问卷测试分数在90.8分以上的概率.
参考数据:若,则,,,,,.
3.2019年某地区初中升学体育考试规定:考生必须参加长跑、掷实心球、1分钟跳绳三项测试.某学校在九年级上学期开始,就为掌握全年级学生1分钟跳绳情况,抽取了100名学生进行测试,得到下面的频率分布直方图.
(1)规定学生1分钟跳绳个数大于等于185为优秀.若在抽取的100名学生中,女生共有50人,男生1分钟跳绳个数大于等于185的有28人.根据已知条件完成下面的2×2列联表,并根据这100名学生的测试成绩,判断能否有99%的把握认为学生1分钟跳绳成绩是否优秀与性别有关.
(2)根据往年经验,该校九年级学生经过训练,正式测试时每人1分钟跳绳个数都有明显进步.假设正式测试时每人1分钟跳绳个数都比九年级上学期开始时增加10个,全年级恰有2000名学生,若所有学生的1分钟跳绳个数X服从正态分布,用样本数据的平均值和标准差估计和,各组数据用中点值代替,估计正式测试时1分钟跳绳个数大于183的人数(结果四舍五入到整数).
附:,其中.
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
若随机变量X服从正态分布,则,,..
4.浙江省东魁杨梅是现在世界上最大果形的杨梅,有“乒乓杨梅”、“杨梅之皇”的美誉.东魁杨梅始于浙江黄岩区江口街道东岙村一棵树龄约120多年的野杨梅树,经过东岙村和白龙岙村村民不断改良,形成了今天东魁杨梅的品种.栽培东魁杨梅一举多得,对开发山区资源,绿化荒山,保持水土,增加山区经济收入具有积极意义.根据多年的经验,可以认为东魁杨梅果实的果径(单位:mm),但因气候、施肥和技术的不同,每年的和都有些变化.现某农场为了了解今年的果实情况,从摘下的杨梅果实中随机取出1000颗,并测量这1000颗果实的果径,得到如下频率分布直方图.
(1)用频率分布直方图估计样本的平均数近似代替,标准差s近似代替,已知.根据以往经验,把果径与的差的绝对值在内的果实称为“标准果”.现从农场中摘取20颗果,请问这20颗果恰好有一颗不是“标准果”的概率;(结果精确到0.01)
(2)随着直播带货的发展,该农场也及时跟进.网络销售在大大提升销量的同时,也增加了坏果赔付的成本.现该农场有一款“”的主打产品,该产品按盒销售,每盒20颗,售价80元,客户在收到货时如果有坏果,每一个坏果该农场要赔付4元.根据收集到的数据,知若采用款包装盒,成本元,且每盒出现坏果个数满足,若采用款包装盒,成本元,且每盒出现坏果个数满足,(为常数),请运用概率统计的相关知识分析,选择哪款包装盒可以获得更大利润
参考数据:;;;;;.
5.某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,记其质量指标值为,当时,产品为一级品;当时,产品为二级品:当时,产品为三级品.现用两种新工艺(分别称为A工艺和B工艺)做实验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面实验结果:(以下均视频率为概率).
A工艺的频数分布表:
指标值分组
频数 10 30 40 20
B工艺的频数分布表:
指标值分组
频数 5 10 15 40 30
(1)若从B工艺产品中有放回地随机抽取4件,记“抽出的B工艺产品中至多有2件二级品”为事件C,求事件C的概率;
(2)若两种新产品的利润率y与质量指标值k满足如下关系:(其中).应用统计知识,请说明最好投资哪种工艺?
6.某企业发明了一种新产品,其质量指标值为,其质量指标等级如下表:
质量指标值m
质量指标等级 良好 优秀 良好 合格 废品
为了解该产品的经济效益并及时调整生产线,该企业先进行试生产.现从试生产的产品中随机抽取了1000件,将其质量指标值m的数据作为样本,绘制如下频率分布直方图:
(1)若将频率作为概率,从该产品中随机抽取2件产品,求抽出的产品中至少有1件不是废品的概率;
(2)若从质量指标值的样本中利用分层抽样的方法抽取7件产品,然后从这7件产品中任取3件产品,求的件数X的分布列及数学期望;
(3)若每件产品的质量指标值m与利润y(单位:万元)的关系如下表():
质量指标值m
利润y(元) 4t 9t 4t 2t
试分析生产该产品能否盈利?若不能,请说明理由;若能,试确定t为何值时,每件产品的平均利润达到最大.
7.某校高三年级举行元宵喜乐会,两人一组猜灯谜,每轮游戏中,每小组两人各猜灯谜两次,猜对灯谜的次数之和不少于3次就可以获得“最佳拍档”称号.甲乙两人同一小组,甲和乙猜对灯谜的概率分别为,.
(1)若,,求在第一轮游戏中他俩就获得“最佳拍档”称号的概率;
(2)若,且在前n轮游戏中甲乙两人的小组获得“最佳拍档”称号的次数的期望为16次,则n的最小值是多少?并求此时的,的值.
8.某超市计划按月订购一种冰激凌,每天进货量相同,进货成本为每桶5元,售价为每桶7元,未售出的冰激凌以每桶3元的价格当天全部处理完毕,根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关,如果最高气温不低于25 ℃,需求量为600桶,如果最高气温(单位:℃)位于区间[20,25),需求量为400桶,如果最高气温低于20 ℃,需求量为200桶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高 气温 (℃) [10,15) [15,20) [20,25) [25,30) [30,35) [35,40]
天数 2 16 36 25 7 4
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种冰激凌一天的需求量X(单位:桶)的分布列;
(2)设六月份一天销售这种冰激凌的利润为Y(单位:元),当六月份这种冰激凌一天的进货量n(单位:桶)为多少时,Y的均值取得最大值?
【答案详解】
1.【详解】
(1)由频率分布直方图可知,各区间对应的频数分布表如下:
成绩区间
频数 5 15 40 75 45 20
∴,
.
(2)①由(1)知服从正态分布,且,
∴.
②依题意,知,
则.
2.【详解】(1)由频率分布直方图可知年龄在上的占比为,
根据已知人数为10计算可得总人数为80,列联表如下:
返赣人员 本地人员 合计
男 25 15 40
女 10 30 40
合计 35 45 80
∴,
所以有99.9%的把握认为是否是从外地回来过年与性别相关.
(2)X的取值可为0,1,2,3,
,,
,.
故分布列为:
X 0 1 2 3
P
于是.
3.【详解】(1)设“从这100箱橙子中随机抽取1箱,抽到一级品”为事件A,则,
现有放回地随机抽取4箱,设抽到一级品的箱数为,则,
所以恰好有2箱是一级品的概率为.
(2)设方案二中每千克橙子的价格为元,
则,
因为,所以从采购商的角度考虑应该采用方案一.
(3)用分层随机抽样的方法从这100箱橙子中抽取10箱,其中珍品4箱,非珍品6箱,
再从中随机抽取3箱,则珍品的箱数X服从超几何分布,其中,,,
,,,.
X的分布列为:
X 0 1 2 3
P
.
4.【详解】(1)由题意知可能取值为300,400,500,600,
则,,
,,
∴当决策部门对甲企业进行精准指导、对乙企业进行综合指导时,两家企业增加的总收入的分布列为
300 400 500 600
0.14 0.56 0.06 0.24
(2)指导方案1:对甲、乙两家企业均进行精准指导.设两家企业增加的总收入为万元,则可能取值为200,300,400,
且,,
,(万元);
指导方案2:对甲企业进行精准指导、对乙企业进行综合指导.
由(1)得(万元);
指导方案3:对甲企业进行综合指导、对乙企业进行精准指导.
设两家企业增加的总收入为,则的可能取值为300,400,500,600,
且,,
,,
(万元).
∵,
∴指导方案3:对甲企业进行综合指导、对乙企业进行精准指导总收入最高.
【过关训练】
1.【详解】(1)由频率分布直方图可得:
采用实验方案大果的数量为个,
则非大果数量为个,
未采用实验方案大果的数量为个,
则非大果数量为个,
列联表如下:
采用实验方案 未采用实验方案 合计
大果
非大果
合计
,所以有的把握认为两者有关;
(2)由题中数据,,
则,
则.
2.【详解】(1)由题意得各组的频率依次为0.1,0.25,0.4,0.15,0.1,
则平均数;
方差
.
(2)(i)由(1)得,,故学生校史问卷测试分数近似服从正态分布,
则
.
(ii),
故随机抽取一名学生,测试分数在90.8分以上的概率为0.0228.
设“这6个人中至少有1入校史问卷测试分数在90.8分以上”为事件,
则,
故这6个人中至少有1入校史问卷测试分数在90.8分以上的概率为0.13.
3.【详解】(1)由频率分布直方图得样本中1分钟跳绳个数大于等于185的人数为
.
补充完整的2×2列联表如下表所示:
由公式可得.
因为,所以没有99%的把握认为学生1分钟跳绳成绩是否优秀与性别有关.
(2)由题知,训练后学生1分钟平均跳绳数比训练前学生1分钟平均跳绳数大10,方差不变.
由直方图计算可得训练前学生1分钟跳绳数的平均数为:,
所以.
训练前学生1分钟跳绳数的方差为:
所以
故X服从正态分布.
,.
故估计正式测试时1分钟跳绳个数大于183的人数约为1683.
4.【详解】(1)由题意得:,所以,,则,,所以,设从农场中摘取20颗果,这20颗果恰好有一颗不是“标准果”为事件A,则
(2)由,解得:,所以,采用A款包装盒获得利润的数学期望,
采用B款包装盒获得利润的数学期望,
令,解得:a=,
由于,令,解得:,
令,解得:,
故当时,采用两种包装利润一样,当时,采用B款包装盒,当时,采用A款包装盒.
5.【详解】(1)抽中二级品的概率,没抽中二级品的概率,
所以抽出的工艺产品中至多2件二级品的概率.
(2)的分布列为:
y t
P 0.6 0.4
则,
的分布列为:
y t
P 0.7 0.25 0.05
则,
所以,
由于时,所以,所以从长期来看,投资工艺的产品平均利润率较大,最好投资工艺.
6.【详解】(1)设抽出的产品中至少有1件不是废品为事件的,其概率为,则由频率分布直方图可得,抽出1件产品为废品的概率为,
则,
(2)由频率分布直方图得指标值大于或等于85的产品中,
,的频率为,
,的频率为,
,的频率为,
利用分层抽样抽取的7件产中,,的有4件,,的有2件,,的有1件,
从这7件产品中,任取3件,质量指标值,的件数的所有可能取值为0,1,2,
则,,,
的分布列为:
0 1 2
.
(3)解:由频率分布直方图可得该产品的质量指标值与利润(元的关系与表所示,
质量指标值
利润
0.3 0.4 0.15 0.1 0.05
每件产品的利润:
,,令,即,解得,因为,所以,即该产品能盈利;
又,所以当时;
7.【详解】
(1)解:由题意,在“第一轮游戏中他俩就获得最佳拍档称号”为事件A,
则.
(2)解:他们在第一轮游戏中获得“最佳拍档”称号的概率为
,
由于,,因此,故,
令,则,
当时,可得,
甲乙两人小组前n轮游戏中获得“最佳拍档”称号的次数,
由,知.
所以n的最小值是,此时.
8.【详解】
(1)由已知得,X的所有可能取值为200,400,600,记六月份最高气温低于20 ℃为事件A1,最高气温(单位:℃)位于区间[20,25)为事件A2,最高气温不低于25 ℃为事件A3,根据题意,结合频数分布表,用频率估计概率,可知
P(X=200)=P(A1)==,
P(X=400)=P(A2)==,
P(X=600)=P(A3)==,
故六月份这种冰激凌一天的需求量X(单位:桶)的分布列为
X 200 400 600
P
(2)由题意得,当n≤200时,E(Y)=2n≤400;
当200当400E(Y)=×[200×2+(n-200)×(-2)]+×[400×2+(n-400)×(-2)]+×n×2=-n+800∈[560,640);
当n>600时,
E(Y)=×[200×2+(n-200)×(-2)]+×[400×2+(n-400)×(-2)]+×[600×2+(n-600)×(-2)]=1 760-2n<560.
所以当n=400时,Y的均值取得最大值640.
概率与统计内容在考试考查中逐步呈现出综合性、应用性和创新性等特点,该题目的设置常常以社会、经济、科技发展为背景,以考生比较熟悉的实际应用问题为载体,考查学生统计图表的识别,应用基础知识和基本方法分析问题和解决问题的能力,充分体现了概率与统计的工具性和交汇性.
统计图表与正态分布
1.为建立健全国家学生体质健康监测评价机制,激励学生积极参加身体锻炼,教育部印发《国家学生体质健康标准(2014年修订)》(简称《标准》),要求各学校每学年开展覆盖本校各年级学生的《标准》测试工作,并依据学生学年总分评定等级.某市在高三年级开展了一次体质健康模拟测试(满分100分),从中随机抽取了200名学生的测试成绩,并据此绘制了如图所示的频率分布直方图.
(1)估计这200名学生测试成绩的平均数和方差(同一组数据用该组区间的中点值作代表).
(2)由频率分布直方图知,该市高三学生的健康指数服从正态分布,其中近似为样本平均数,近似为样本方差.
①求;
②已知该市高三学生约有10000名,记测试成绩在区间的人数为,求.
附:参考数据.若随机变量服从正态分布,则,,.
统计图表与统计分析
2.2022年2月1日是春节,百节年为首,春节是中华民族最隆重的传统佳节,它不仅集中体现了中华民族的思想信仰、理想愿望、生活娱乐和文化心理,而且还是祈福攮灾、饮食和娛乐活动的狂欢式展示.为调查某地从外地工作回来过年的市民(以下称为“返赣人员”)人数情况,现对某一区域的居民进行抽样调查,并按年龄(单位:岁)分成五组,得到如图所示的频率分布直方图,其中年龄在内的人数为10.
(1)请根据样本数据补充完成列联表,并判断是否有99.9%的把握认为是否是从外地回来过年与性别相关;
返赣人员 本地人员 合计
男 15
女 10 40
合计
(2)据了解,该地区今年返赣人员占.现从该社区居民中随机抽取3人进行调查,记X为这3人中今年是返赣人员的人数,求X的分布列与数学期望.
参考公式:,其中.参考数据:
0.10 0.05 0.010 0.001
2.706 3.841 6.635 10.828
三、概率统计中的决策问题
3.某冰糖橙是甜橙的一种,以味甜皮薄著称.该橙按照等级可分为四类:珍品、特级、优级和一级.某采购商打算订购一批橙子销往省外,并从采购的这批橙子中随机抽取100箱(每箱有5kg),利用橙子的等级分类标准得到的数据如下表:
等级 珍品 特级 优级 一级
箱数 40 30 10 20
(1)若将频率作为概率,从这100箱橙子中有放回地随机抽取4箱,求恰好有2箱是一级品的概率;
(2)利用样本估计总体,果园老板提出两种方案供采购商参考:方案一:不分等级出售,价格为27元/kg;方案二:分等级出售,橙子价格如下表.
等级 珍品 特级 优级 一级
价格/(元∕kg) 36 30 24 18
从采购商的角度考虑,应该采用哪种方案?
(3)用分层随机抽样的方法从这100箱橙子中抽取10箱,再从抽取的10箱中随机抽取3箱,X表示抽取的珍品的箱数,求X的分布列及均值.
四、概率统计中的最值问题
4.在中国共产党的正确领导下,我国顺利实现了第一个百年奋斗目标——全面建成小康社会.某地为了巩固扶贫成果,决定继续对甲、乙两家乡镇企业进行指导.指导方式有两种,一种是精准指导,一种是综合指导.已知对甲企业采用精准指导时,投资50万元,增加100万元收入的概率为0.2,增加200万元收入的概率为0.8,采用综合指导时,投资100万元,增加200万元收入的概率为0.6,增加400万收入的概率为0.4;对乙企业采用精准指导时,投资50万元,增加100万元收入的概率为0.3,增加200万元收入的概率为0.7,采用综合指导时,投资100万元,增加200万元收入的概率为0.7,增加400万元收入的概率为0.3.指导结果在两家企业之间互不影响.
(1)若决策部门对甲企业进行精准指导、对乙企业进行综合指导,设两家企业增加的总收入为万元,求的分布列;
(2)若有150万元无息贷款可供甲、乙两家企业使用,对两家企业应分别进行哪种指导总收入最高?请说明理由.
【过关训练】
1.科研小组为提高某种水果的果径,设计了一套实验方案,并在两片果园中进行对比实验.其中实验园采用实验方案,对照园未采用.实验周期结束后,分别在两片果园中各随机选取100个果实,按果径分成5组进行统计:,,,,(单位:).统计后分别制成如下的频率分布直方图,并规定果径达到36及以上的为“大果”.
(1)请根据题中信息完成下面的列联表,并判断是否有的把握认为“大果”与“采用实验方案”有关;
采用实验方案 未采用实验方案 合计
大果
非大果
合计 100 100 200
(2)根据长期种植经验,可以认为对照园中的果径服从正态分布,其中近似为样本平均数,,请估计对照园中果径落在区间内的概率.(同一组中的数据以这组数据所在区间中点的值作代表)
附:①;
②若服从正态分布,则,,.
2.中国人民解放军装甲兵学院(前身蚌埠坦克学院),建校至今为我国培养了一大批优秀的军事人才.在今年新入学的学生中,为了加强爱校教育,现在从全体新入学的学生中随机的抽取了100人,对他们进行校史问卷测试,得分在45~95之间,分为,,,,五组,得到如图所示的频率分布直方图,其中第三组的频数为40.
(1)请根据频率分布直方图估计样本的平均数和方差(同一组中的数据用该组区间的中点值代表);
(2)根据样本数据,可认为新人学的学生校史问卷测试分数近似服从正态分布,其中近似为样本平均数,近似为样本方差.
(i)求;
(ii)在某间寝室有6人,求这6个人中至少有1人校史问卷测试分数在90.8分以上的概率.
参考数据:若,则,,,,,.
3.2019年某地区初中升学体育考试规定:考生必须参加长跑、掷实心球、1分钟跳绳三项测试.某学校在九年级上学期开始,就为掌握全年级学生1分钟跳绳情况,抽取了100名学生进行测试,得到下面的频率分布直方图.
(1)规定学生1分钟跳绳个数大于等于185为优秀.若在抽取的100名学生中,女生共有50人,男生1分钟跳绳个数大于等于185的有28人.根据已知条件完成下面的2×2列联表,并根据这100名学生的测试成绩,判断能否有99%的把握认为学生1分钟跳绳成绩是否优秀与性别有关.
(2)根据往年经验,该校九年级学生经过训练,正式测试时每人1分钟跳绳个数都有明显进步.假设正式测试时每人1分钟跳绳个数都比九年级上学期开始时增加10个,全年级恰有2000名学生,若所有学生的1分钟跳绳个数X服从正态分布,用样本数据的平均值和标准差估计和,各组数据用中点值代替,估计正式测试时1分钟跳绳个数大于183的人数(结果四舍五入到整数).
附:,其中.
0.15 0.10 0.05 0.025 0.010 0.005 0.001
2.072 2.706 3.841 5.024 6.635 7.879 10.828
若随机变量X服从正态分布,则,,..
4.浙江省东魁杨梅是现在世界上最大果形的杨梅,有“乒乓杨梅”、“杨梅之皇”的美誉.东魁杨梅始于浙江黄岩区江口街道东岙村一棵树龄约120多年的野杨梅树,经过东岙村和白龙岙村村民不断改良,形成了今天东魁杨梅的品种.栽培东魁杨梅一举多得,对开发山区资源,绿化荒山,保持水土,增加山区经济收入具有积极意义.根据多年的经验,可以认为东魁杨梅果实的果径(单位:mm),但因气候、施肥和技术的不同,每年的和都有些变化.现某农场为了了解今年的果实情况,从摘下的杨梅果实中随机取出1000颗,并测量这1000颗果实的果径,得到如下频率分布直方图.
(1)用频率分布直方图估计样本的平均数近似代替,标准差s近似代替,已知.根据以往经验,把果径与的差的绝对值在内的果实称为“标准果”.现从农场中摘取20颗果,请问这20颗果恰好有一颗不是“标准果”的概率;(结果精确到0.01)
(2)随着直播带货的发展,该农场也及时跟进.网络销售在大大提升销量的同时,也增加了坏果赔付的成本.现该农场有一款“”的主打产品,该产品按盒销售,每盒20颗,售价80元,客户在收到货时如果有坏果,每一个坏果该农场要赔付4元.根据收集到的数据,知若采用款包装盒,成本元,且每盒出现坏果个数满足,若采用款包装盒,成本元,且每盒出现坏果个数满足,(为常数),请运用概率统计的相关知识分析,选择哪款包装盒可以获得更大利润
参考数据:;;;;;.
5.某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,记其质量指标值为,当时,产品为一级品;当时,产品为二级品:当时,产品为三级品.现用两种新工艺(分别称为A工艺和B工艺)做实验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面实验结果:(以下均视频率为概率).
A工艺的频数分布表:
指标值分组
频数 10 30 40 20
B工艺的频数分布表:
指标值分组
频数 5 10 15 40 30
(1)若从B工艺产品中有放回地随机抽取4件,记“抽出的B工艺产品中至多有2件二级品”为事件C,求事件C的概率;
(2)若两种新产品的利润率y与质量指标值k满足如下关系:(其中).应用统计知识,请说明最好投资哪种工艺?
6.某企业发明了一种新产品,其质量指标值为,其质量指标等级如下表:
质量指标值m
质量指标等级 良好 优秀 良好 合格 废品
为了解该产品的经济效益并及时调整生产线,该企业先进行试生产.现从试生产的产品中随机抽取了1000件,将其质量指标值m的数据作为样本,绘制如下频率分布直方图:
(1)若将频率作为概率,从该产品中随机抽取2件产品,求抽出的产品中至少有1件不是废品的概率;
(2)若从质量指标值的样本中利用分层抽样的方法抽取7件产品,然后从这7件产品中任取3件产品,求的件数X的分布列及数学期望;
(3)若每件产品的质量指标值m与利润y(单位:万元)的关系如下表():
质量指标值m
利润y(元) 4t 9t 4t 2t
试分析生产该产品能否盈利?若不能,请说明理由;若能,试确定t为何值时,每件产品的平均利润达到最大.
7.某校高三年级举行元宵喜乐会,两人一组猜灯谜,每轮游戏中,每小组两人各猜灯谜两次,猜对灯谜的次数之和不少于3次就可以获得“最佳拍档”称号.甲乙两人同一小组,甲和乙猜对灯谜的概率分别为,.
(1)若,,求在第一轮游戏中他俩就获得“最佳拍档”称号的概率;
(2)若,且在前n轮游戏中甲乙两人的小组获得“最佳拍档”称号的次数的期望为16次,则n的最小值是多少?并求此时的,的值.
8.某超市计划按月订购一种冰激凌,每天进货量相同,进货成本为每桶5元,售价为每桶7元,未售出的冰激凌以每桶3元的价格当天全部处理完毕,根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关,如果最高气温不低于25 ℃,需求量为600桶,如果最高气温(单位:℃)位于区间[20,25),需求量为400桶,如果最高气温低于20 ℃,需求量为200桶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
最高 气温 (℃) [10,15) [15,20) [20,25) [25,30) [30,35) [35,40]
天数 2 16 36 25 7 4
以最高气温位于各区间的频率代替最高气温位于该区间的概率.
(1)求六月份这种冰激凌一天的需求量X(单位:桶)的分布列;
(2)设六月份一天销售这种冰激凌的利润为Y(单位:元),当六月份这种冰激凌一天的进货量n(单位:桶)为多少时,Y的均值取得最大值?
【答案详解】
1.【详解】
(1)由频率分布直方图可知,各区间对应的频数分布表如下:
成绩区间
频数 5 15 40 75 45 20
∴,
.
(2)①由(1)知服从正态分布,且,
∴.
②依题意,知,
则.
2.【详解】(1)由频率分布直方图可知年龄在上的占比为,
根据已知人数为10计算可得总人数为80,列联表如下:
返赣人员 本地人员 合计
男 25 15 40
女 10 30 40
合计 35 45 80
∴,
所以有99.9%的把握认为是否是从外地回来过年与性别相关.
(2)X的取值可为0,1,2,3,
,,
,.
故分布列为:
X 0 1 2 3
P
于是.
3.【详解】(1)设“从这100箱橙子中随机抽取1箱,抽到一级品”为事件A,则,
现有放回地随机抽取4箱,设抽到一级品的箱数为,则,
所以恰好有2箱是一级品的概率为.
(2)设方案二中每千克橙子的价格为元,
则,
因为,所以从采购商的角度考虑应该采用方案一.
(3)用分层随机抽样的方法从这100箱橙子中抽取10箱,其中珍品4箱,非珍品6箱,
再从中随机抽取3箱,则珍品的箱数X服从超几何分布,其中,,,
,,,.
X的分布列为:
X 0 1 2 3
P
.
4.【详解】(1)由题意知可能取值为300,400,500,600,
则,,
,,
∴当决策部门对甲企业进行精准指导、对乙企业进行综合指导时,两家企业增加的总收入的分布列为
300 400 500 600
0.14 0.56 0.06 0.24
(2)指导方案1:对甲、乙两家企业均进行精准指导.设两家企业增加的总收入为万元,则可能取值为200,300,400,
且,,
,(万元);
指导方案2:对甲企业进行精准指导、对乙企业进行综合指导.
由(1)得(万元);
指导方案3:对甲企业进行综合指导、对乙企业进行精准指导.
设两家企业增加的总收入为,则的可能取值为300,400,500,600,
且,,
,,
(万元).
∵,
∴指导方案3:对甲企业进行综合指导、对乙企业进行精准指导总收入最高.
【过关训练】
1.【详解】(1)由频率分布直方图可得:
采用实验方案大果的数量为个,
则非大果数量为个,
未采用实验方案大果的数量为个,
则非大果数量为个,
列联表如下:
采用实验方案 未采用实验方案 合计
大果
非大果
合计
,所以有的把握认为两者有关;
(2)由题中数据,,
则,
则.
2.【详解】(1)由题意得各组的频率依次为0.1,0.25,0.4,0.15,0.1,
则平均数;
方差
.
(2)(i)由(1)得,,故学生校史问卷测试分数近似服从正态分布,
则
.
(ii),
故随机抽取一名学生,测试分数在90.8分以上的概率为0.0228.
设“这6个人中至少有1入校史问卷测试分数在90.8分以上”为事件,
则,
故这6个人中至少有1入校史问卷测试分数在90.8分以上的概率为0.13.
3.【详解】(1)由频率分布直方图得样本中1分钟跳绳个数大于等于185的人数为
.
补充完整的2×2列联表如下表所示:
由公式可得.
因为,所以没有99%的把握认为学生1分钟跳绳成绩是否优秀与性别有关.
(2)由题知,训练后学生1分钟平均跳绳数比训练前学生1分钟平均跳绳数大10,方差不变.
由直方图计算可得训练前学生1分钟跳绳数的平均数为:,
所以.
训练前学生1分钟跳绳数的方差为:
所以
故X服从正态分布.
,.
故估计正式测试时1分钟跳绳个数大于183的人数约为1683.
4.【详解】(1)由题意得:,所以,,则,,所以,设从农场中摘取20颗果,这20颗果恰好有一颗不是“标准果”为事件A,则
(2)由,解得:,所以,采用A款包装盒获得利润的数学期望,
采用B款包装盒获得利润的数学期望,
令,解得:a=,
由于,令,解得:,
令,解得:,
故当时,采用两种包装利润一样,当时,采用B款包装盒,当时,采用A款包装盒.
5.【详解】(1)抽中二级品的概率,没抽中二级品的概率,
所以抽出的工艺产品中至多2件二级品的概率.
(2)的分布列为:
y t
P 0.6 0.4
则,
的分布列为:
y t
P 0.7 0.25 0.05
则,
所以,
由于时,所以,所以从长期来看,投资工艺的产品平均利润率较大,最好投资工艺.
6.【详解】(1)设抽出的产品中至少有1件不是废品为事件的,其概率为,则由频率分布直方图可得,抽出1件产品为废品的概率为,
则,
(2)由频率分布直方图得指标值大于或等于85的产品中,
,的频率为,
,的频率为,
,的频率为,
利用分层抽样抽取的7件产中,,的有4件,,的有2件,,的有1件,
从这7件产品中,任取3件,质量指标值,的件数的所有可能取值为0,1,2,
则,,,
的分布列为:
0 1 2
.
(3)解:由频率分布直方图可得该产品的质量指标值与利润(元的关系与表所示,
质量指标值
利润
0.3 0.4 0.15 0.1 0.05
每件产品的利润:
,,令,即,解得,因为,所以,即该产品能盈利;
又,所以当时;
7.【详解】
(1)解:由题意,在“第一轮游戏中他俩就获得最佳拍档称号”为事件A,
则.
(2)解:他们在第一轮游戏中获得“最佳拍档”称号的概率为
,
由于,,因此,故,
令,则,
当时,可得,
甲乙两人小组前n轮游戏中获得“最佳拍档”称号的次数,
由,知.
所以n的最小值是,此时.
8.【详解】
(1)由已知得,X的所有可能取值为200,400,600,记六月份最高气温低于20 ℃为事件A1,最高气温(单位:℃)位于区间[20,25)为事件A2,最高气温不低于25 ℃为事件A3,根据题意,结合频数分布表,用频率估计概率,可知
P(X=200)=P(A1)==,
P(X=400)=P(A2)==,
P(X=600)=P(A3)==,
故六月份这种冰激凌一天的需求量X(单位:桶)的分布列为
X 200 400 600
P
(2)由题意得,当n≤200时,E(Y)=2n≤400;
当200
当n>600时,
E(Y)=×[200×2+(n-200)×(-2)]+×[400×2+(n-400)×(-2)]+×[600×2+(n-600)×(-2)]=1 760-2n<560.
所以当n=400时,Y的均值取得最大值640.
