人教A版2019选择性必修第三册8.3 列联表与独立性检验 学案(Word版含答案)
文档属性
| 名称 | 人教A版2019选择性必修第三册8.3 列联表与独立性检验 学案(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 00:00:00 | ||
图片预览


文档简介
8.3 列联表与独立性检验
【知识梳理】
知识点一 分类变量
为了表述方便,我们经常会使用一种特殊的随机变量,以区别不同的现象或性质,这类随机变量称为分类变量.
分类变量的取值可以用实数表示.
知识点二 2×2列联表
1.2×2列联表给出了成对分类变量数据的交叉分类频数.
2.定义一对分类变量X和Y,我们整理数据如下表所示:
X Y 合计
Y=0 Y=1
X=0 a b a+b
X=1 c d c+d
合计 a+c b+d n=a+b+c+d
像这种形式的数据统计表称为2×2列联表.
知识点三 独立性检验
1.定义:利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2独立性检验,读作“卡方独立性检验”.简称独立性检验.
2.χ2=,其中n=a+b+c+d.
3.独立性检验解决实际问题的主要环节
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
【题型归纳】
一、等高堆积条形图的应用
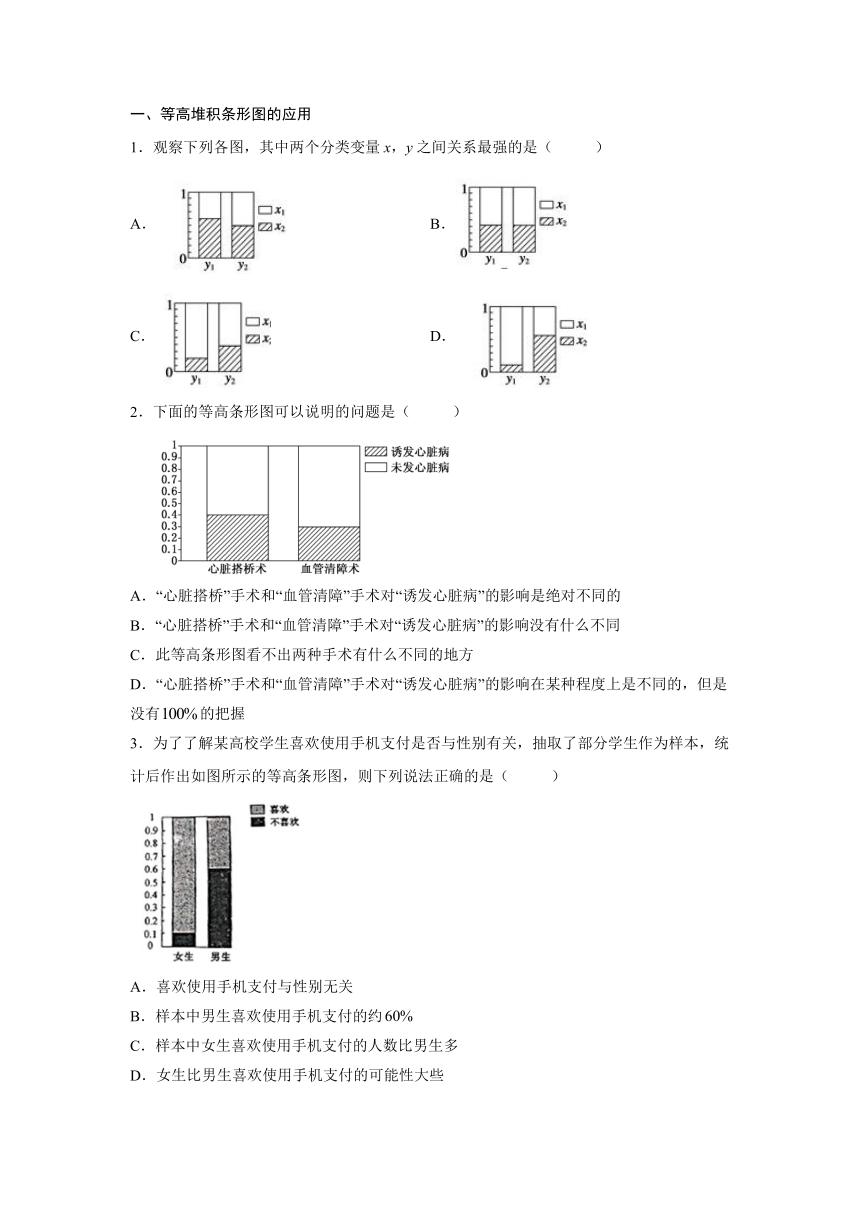
1.观察下列各图,其中两个分类变量x,y之间关系最强的是( )
A. B.
C. D.
2.下面的等高条形图可以说明的问题是( )
A.“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响是绝对不同的
B.“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响没有什么不同
C.此等高条形图看不出两种手术有什么不同的地方
D.“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响在某种程度上是不同的,但是没有的把握
3.为了了解某高校学生喜欢使用手机支付是否与性别有关,抽取了部分学生作为样本,统计后作出如图所示的等高条形图,则下列说法正确的是( )
A.喜欢使用手机支付与性别无关
B.样本中男生喜欢使用手机支付的约
C.样本中女生喜欢使用手机支付的人数比男生多
D.女生比男生喜欢使用手机支付的可能性大些
二、由χ2进行独立性检验
命题角度1 有关“相关的检验”
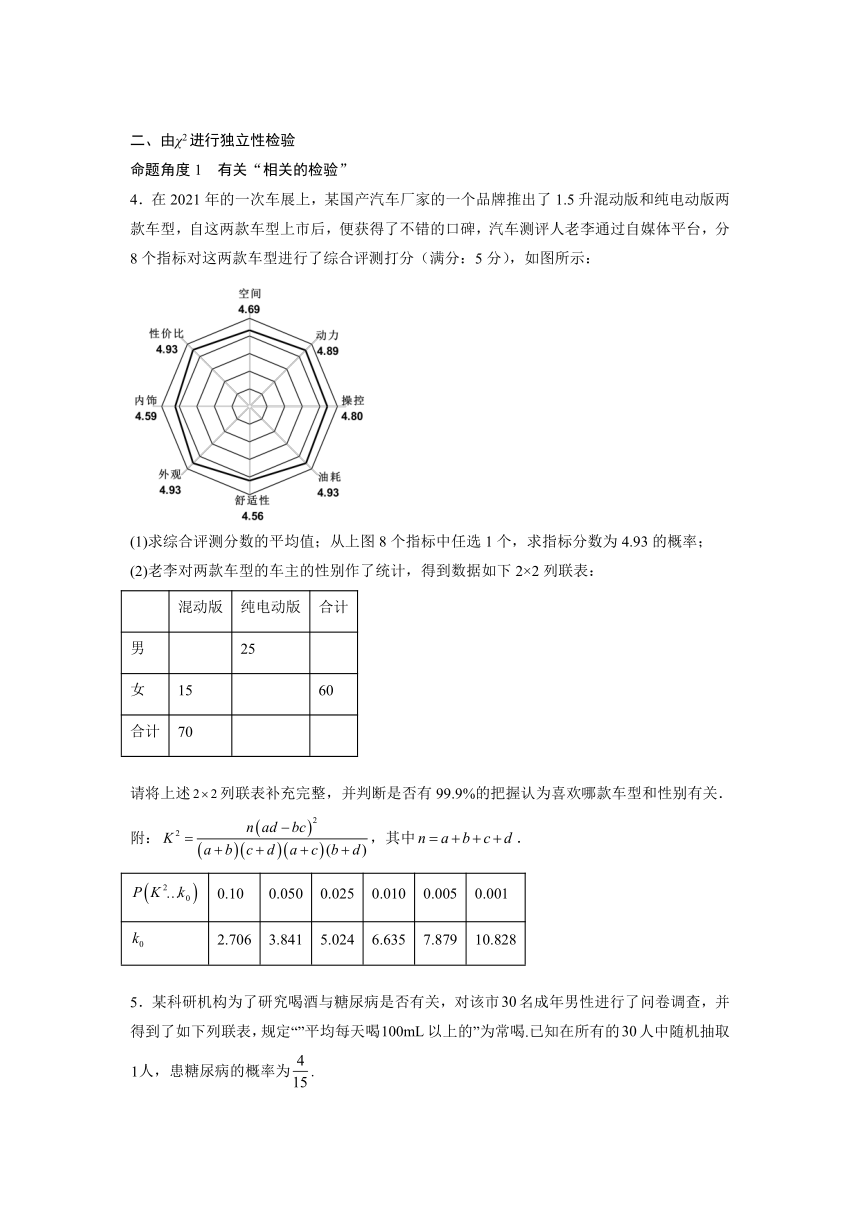
4.在2021年的一次车展上,某国产汽车厂家的一个品牌推出了1.5升混动版和纯电动版两款车型,自这两款车型上市后,便获得了不错的口碑,汽车测评人老李通过自媒体平台,分8个指标对这两款车型进行了综合评测打分(满分:5分),如图所示:
(1)求综合评测分数的平均值;从上图8个指标中任选1个,求指标分数为4.93的概率;
(2)老李对两款车型的车主的性别作了统计,得到数据如下2×2列联表:
混动版 纯电动版 合计
男 25
女 15 60
合计 70
请将上述列联表补充完整,并判断是否有99.9%的把握认为喜欢哪款车型和性别有关.
附:,其中.
0.10 0.050 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
5.某科研机构为了研究喝酒与糖尿病是否有关,对该市名成年男性进行了问卷调查,并得到了如下列联表,规定“”平均每天喝以上的”为常喝.已知在所有的人中随机抽取人,患糖尿病的概率为.
常喝 不常喝 合计
有糖尿病
无糖尿病
合计
(1)请将上表补充完整,并判断是否有的把握认为糖尿病与喝酒有关?请说明理由;
(2)已知常喝酒且有糖尿病的人中恰有两名老年人,其余为中年人,现从常喝酒且有糖尿病的这人中随机抽取人,求恰好抽到一名老年人和一名中年人的概率.
参考公式及数据:,.
命题角度2 有关“无关的检验”
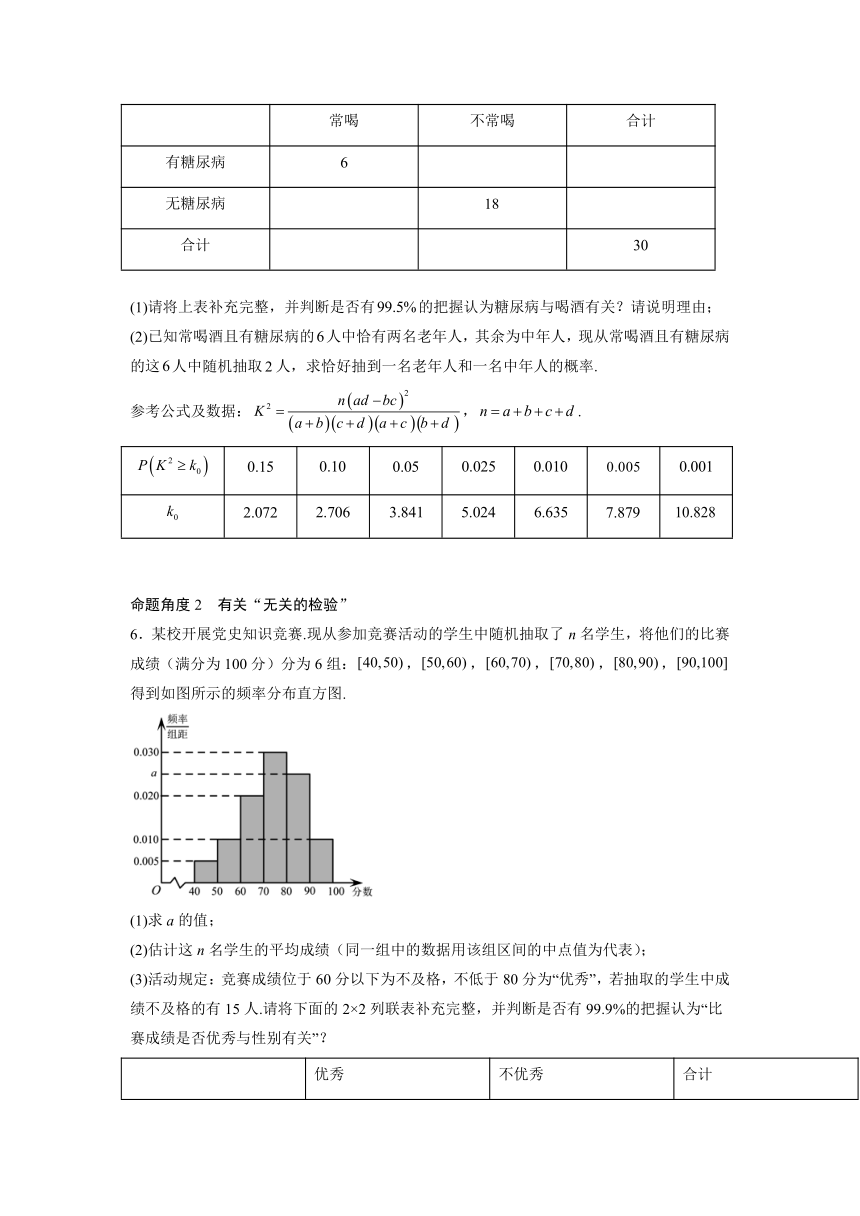
6.某校开展党史知识竞赛.现从参加竞赛活动的学生中随机抽取了n名学生,将他们的比赛成绩(满分为100分)分为6组:,,,,,得到如图所示的频率分布直方图.
(1)求a的值;
(2)估计这n名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(3)活动规定:竞赛成绩位于60分以下为不及格,不低于80分为“优秀”,若抽取的学生中成绩不及格的有15人.请将下面的2×2列联表补充完整,并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 不优秀 合计
男生 40
女生 50
合计
参考公式及数据:,.
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
7.2021年1月以来,教育部相继出台文件,对中小学生手机、睡眠、读物、作业、体质管理作出规定.为了在“控量”的同时力求“增效”,提高作业质量,某学校计划设计差异化作业.因此该校对初三年级的400名学生每天完成作业所需时间进行统计,部分数据如下表:
单位:人
完成作业所需时间 性别 合计
男生 女生
90分钟以上 80 x 180
90分钟及以下 y z 220
合计 160 240 400
(1)求x,y,z的值,并根据题中的列联表,依据小概率值的独立性检验,判断是否可以认为完成作业所需时间在90分钟以上与性别有关;
(2)学校从完成作业所需时间在90分钟以上的学生中用分层随机抽样的方法抽取9人了解情况,甲老师再从这9人中选取3人进行访谈,求甲老师选取的3人中男生人数大于女生人数的概率.
附:
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
参考公式:,.
【双基达标】
1.某省二线城市地铁正式开工建设,地铁时代的到来能否缓解该市的交通拥堵状况呢 某社团进行社会调查,得到的数据如下表:
男性市民 女性市民
认为能缓解交通拥堵
认为不能缓解交通拥堵
则下列结论中正确的是( )A.有的把握认为“对能否缓解交通拥堵的认识与性别有关”
B.有的把握认为“对能否缓解交通拥堵的认识与性别无关”
C.有的把握认为“对能否缓解交通拥堵的认识与性别有关”
D.有的把握认为“对能否缓解交通拥堵的认识与性别无关”
2.某学校食堂对高三学生偏爱蔬菜还是肉类与性别的关系进行了一次调查,根据独立性检验原理,处理所得数据之后发现,有的把握但没有的把握认为偏爱蔬菜还是肉类与性别有关,则的值可能为( )
附表:
A. B.
C. D.
3.在利用统计量来判断两个变量与之间是否有关系时,下列说法正确的是( )
A.越大,“与有关系”的可信程度越小
B.越小,“与有关系”的可信程度越小
C.越接近于0,“与没有关系”的可信程度越小
D.越大,“与没有关系”的可信程度越大
4.假设有两个变量X和Y,他们的取值分别为,和,,其列联表为:
总计
21 73
8 25 33
总计 46 106
则表中,的值分别是( )
A.94,96 B.54,52 C.52,50 D.52,60
5.为考查A,B两种药物预防某疾病的效果,进行动物实验,分别得到如下等高条形图:根据图中信息,在下列各项中,说法最佳的一项是( )
A.药物B的预防效果优于药物A的预防效果
B.药物A的预防效果优于药物B的预防效果
C.药物A,B对该疾病均有显著的预防效果
D.药物A,B对该疾病均没有预防效果
6.如图是调查某学校高三年级男女学生是否喜欢数学的等高条形图,阴影部分的高表示喜欢数学的频率.已知该年级男生女生各500名(所有学生都参加了调查),现从所有喜欢数学的同学中按分层抽样的方式抽取32人,则抽取的男生人数为
A.16 B.32 C.24 D.8
7.2021年河北省采用“”新高考模式,其中“3”为全国统考科目语文 数学和外语;“1”为考生在物理和历史中选择一门;“2”为考生在思想政治 地理 化学和生物四门中再选择两门.某中学调查了高一年级学生的选科倾向,随机抽取人,其中选考物理的人,选考历史的人,统计各选科人数如下表,则下列说法正确的是( )
选择科目选考类别 思想政治 地理 化学 生物
物理类 80 100 145 115
历史类 50 45 30 35
附:
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
A.物理类的学生中选择政治的比例比历史类的学生中选择政治的比例高
B.物理类的学生中选择地理的比例比历史类的学生中选择地理的比例高
C.没有以上的把握认为选择生物与选考类别有关
D.有以上的把握认为选择生物与选考类别有关
8.(多选)北京冬奥会临近开幕,大众对冰雪运动关注不断上升,各地陆续建成众多冰雪设施,广大市民有条件体验冰雪活动的乐趣,为研究市民性别和喜欢冰雪活动是否有关,某校社团学生在部分市民中进行了一次调查,得到下表:
冰雪运动的喜好 性别 合计
男性 女性
喜欢 140 m 140+m
不喜欢 n 80 80+n
合计 140+n 80+m 220+m+n
已知男性喜欢冰雪运动的人数占男性人数的,女性喜欢冰雪运动的人数占女性人数的,则( )
参考:,P(>3.841)=0.05,P(>6.635)=0.01.
A.列联表中n的值为60,m的值为120
B.有95%的把握认为市民性别和喜欢冰雪运动有关系
C.随机对一路人进行调查,有95%的可能性对方喜欢冰雪运动
D.没有99%的把握认为市民性别和喜欢冰雪运动有关系
9.针对“中学生追星问题”,某校团委对“学生性别和中学生追星是否有关”作了一次调查,其中女生人数是男生人数的,男生追星的人数占男生人数的,女生追星的人数占女生人数的,若有的把握认为中学生追星与性别有关,则男生至少有__________人.
参考数据及公式如下:
0.050 0.010 0.001
3.841 6.635 10.828
,.
10.某部门为了解人们对“延迟退休年龄政策”的支持度,随机调查了人,其中男性人.调查发现持不支持态度的有人,其中男性占.分析这个持不支持态度的样本的年龄和性别结构,绘制等高条形图如图所示.
(1)在持不支持态度的人中,周岁及以上的男女比例是多少?
(2)调查数据显示,个持支持态度的人中有人年龄在周岁以下.填写下面的列联表,问能否有的把握认为年龄是否在周岁以下与对“延迟退休年龄政策”的态度有关.
参考公式及数据:,.
11.数字人民币是由中国人民银行发行的数字形式的法定货币,由指定运营机构参与运营并向公众兑换,与纸钞和硬币等价.为了进一步了解普通大众对数字人民币的认知情况,某机构进行了一次问卷调查,统计结果如下:
小学及以下 初中 高中 大学专科 大学本科 硕士研究生及以上
不了解数字人民币 35 35 80 55 64 6
了解数字人民币 40 60 150 110 140 25
(1)如果将高中及以下学历称为“低学历”,大学专科及以上学历称为“高学历”,根据所给数据,完成下面的列联表;
低学历 高学历 合计
不了解数字人民币
了解数字人民币
合计 800
(2)根据(1)中所得列联表,判断是否有的把握认为“是否了解数字人民币”与“学历高低”有关?
附:,其中.
0.050 0.010 0.001
K 3.841 6.635 10.828
12.某视频上传者为确定下一段时间的视频制作方向,在动态中发布投票,投票主题为“你希望我接下来更新哪个方向的视频”,共计人参与此投票,投票结果如下图所示(每位关注者仅选一项).
其中,投票游戏、动漫、生活的关注者之比为.
(1)求参与投票的关注者的性别比;
(2)以游戏与生活两个方向为例,依据小概率值的独立性检验,判断性别与关注者喜欢视频上传者上传视频的类型是否有关.
注:;临界值,.
13.晨跑是不少青年爱好者锻炼身体的一种运动方式,某机构随机抽取了某社区200名青年进行问卷调查,其中男性与女性的人数比为3:2,得到如下的列联表,
喜欢晨跑 不喜欢晨跑 合计
男性 40
女性
合计
现从这200名青年中按性别用分层抽样的方法随机抽取20人,其中喜欢晨跑的女性有5人.
(1)完成表中数据并判断是否有90%的把握认为喜欢晨跑与性别有关;
(2)从上述样本中不喜欢晨跑的青年中用分层抽样的方法任取7名,再从这7人中抽取4人调查,其中这4人中的女性人数为X,求X的分布列及数学期望.
参考公式及数据:,其中.
0.10 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
【高分突破】
1.2020年2月,全国掀起了“停课不停学”的热潮,各地教师通过网络直播 微课推送等多种方式来指导学生线上学习.为了调查学生对网络课程的热爱程度,研究人员随机调查了相同数量的男 女学生,发现有80%的男生喜欢网络课程,有40%的女生不喜欢网络课程,且有99%的把握但没有99.9%的把握认为是否喜欢网络课程与性别有关,则被调查的男 女学生总数量可能为( )
附:,其中.
0.1 0.05 0.01 0.001
2.706 3.841 6.635 10.828
A.130 B.190 C.240 D.250
2.某大学为了解喜欢看篮球赛是否与性别有关,随机调查了部分学生,在被调查的学生中,男生人数是女生人数的2倍,男生喜欢看篮球赛的人数占男生人数的,女生喜欢看篮球赛的人数占女生人数的.若被调查的男生人数为,且有95%的把握认为喜欢看篮球赛与性别有关,则的最小值为( )
A.6 B.12 C.18 D.36
3.针对“中学生追星问题”,某校团委对“学生性别和中学生追星是否有关”作了一次调查,调查样本中女生人数是男生人数的,男生追星的人数占男生人数的,女生追星的人数占女生人数的,若有的把握认为是否追星和性别有关,则调查样本中男生至少有( )
参考数据及公式如下:
A.12人 B.11人 C.10人 D.18人
4.以下说法:
①将一组数据中的每一个数据都加上或减去同一个常数后,方差不变;
②设有一个回归方程,变量增加1个单位时,平均增加5个单位
③线性回归方程必过
④设具有相关关系的两个变量的相关系数为,那么越接近于0,之间的线性相关程度越高;
⑤在一个列联表中,由计算得的值,那么的值越大,判断两个变量间有关联的把握就越大。
其中错误的个数是( )
A.0 B.1 C.2 D.3
5.(多选)针对时下的“抖音热”,某校团委对“是否喜欢抖音与学生性别的关系”进行了一次调查,其中被调查的男、女生人数相同,男生中喜欢抖音的人数占男生人数的,女生中喜欢抖音的人数占女生人数的,若有95%的把握认为是否喜欢抖音与学生性别有关,则被调查的学生中男生的人数可能为( )
A.25 B.45
C.60 D.75
6.针对时下的“抖音热”,某校团委对“学生性别和喜欢抖音是否有关”作了一次调查,其中被调查的男女生人数相同,男生喜欢抖音的人数占男生人数的,女生喜欢抖音的人数占女生人数.若有的把握认为是否喜欢抖音和性别有关,则调查人数中男生至少有________人.
7.下列说法:
①线性回归方程必过;
②命题“”的否定是“”
③相关系数越小,表明两个变量相关性越弱;
④在一个列联表中,由计算得,则有的把握认为这两个变量间有关系;
其中正确的说法是__________.(把你认为正确的结论都写在横线上)
本题可参考独立性检验临界值表:
8.2022年是奥运会,我国北京和张家口联合承办第二十四届冬季奥运会,本届冬奥会共设7个大项(滑雪、滑冰、冰球、冰壶、雪车、雪橇、冬季两项)、15个分项(高山滑雪、自由式滑雪、单板滑雪、跳台滑雪、越野滑雪、北欧两项、短道速滑、速度滑冰、花样滑冰、冰球、冰壶、雪车、钢架雪车、雪橇、冬季两项)共计109个小项.某校为了调查学生是否喜欢冬季冰雪运动与性别有关,在高三年级特选取了200名学生进行了问卷调查,得到如下的列联表:
喜欢 不喜欢 合计
男生
女生
合计
已知从这200名学生中随机抽取1人,这个人喜欢冰雪运动的概率为0.8,表格中,.
(1)完成列联表,并判断是否有90%的把握认为喜欢冰雪运动与性别有关;
(2)从上述喜欢冰雪运动的学生中用分层抽样的方法抽取8名学生,再从这8人中抽取3人调查其喜欢的运动,用表示3人中女生的人数,求的分布列及数学期望.
参考公式及数据:,其中.
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.01 0.005 0.001
0.46 0.71 1.32 2.07 2.71 3.84 5.024 6.635 7.879 10.828
9.为了检测某种抗病毒疫苗的免疫效果,需要进行动物与人体试验.研究人员将疫苗注射到200只小白鼠体内,一段时间后测量小白鼠的某项指标值,按,,,,分组,绘制频率分布直方图如图所示.试验发现小白鼠体内产生抗体的共有160只,其中该项指标值不小于60的有110只.假设小白鼠注射疫苗后是否产生抗体相互独立.
(1)填写下面的列联表,并根据列联表及的独立性检验,判断能否认为注射疫苗后小白鼠产生抗体与指标值不小于60有关.
单位:只
抗体 指标值 合计
小于60 不小于60
有抗体
没有抗体
合计
(2)为检验疫苗二次接种的免疫抗体性,对第一次注射疫苗后没有产生抗体的40只小白鼠进行第二次注射疫苗,结果又有20只小白鼠产生抗体.
(i)用频率估计概率,求一只小白鼠注射2次疫苗后产生抗体的概率;
(ii)以(i)中确定的概率作为人体注射2次疫苗后产生抗体的概率,进行人体接种试验,记个人注射2次疫苗后产生抗体的数量为随机变量.试验后统计数据显示,当时,取最大值,求参加人体接种试验的人数及.
参考公式: (其中为样本容量)
参考数据:
0.50 0.40 0.25 0.15 0.100 0.050 0.025
0.455 0.708 1.323 2.072 2.706 3.841 5.024
10.中国职业篮球联赛(CBA联赛)分为常规赛和季后赛.由于新冠疫情关系,今年联赛采用赛会制:所有球队集中在同一个地方比赛,分两个阶段进行,每个阶段采用循环赛,分主场比赛和客场比赛,积分排名前8的球队进入季后赛.季后赛的总决赛采用五场三胜制(“五场三胜制”是指在五场比赛中先胜三场者获得比赛胜利,胜者成为本赛季的总冠军).下表是队在常规赛60场比赛中的比赛结果记录表.
阶段 比赛场数 主场场数 获胜场数 主场获胜场数
第一阶段 30 15 20 10
第二阶段 30 15 25 15
(1)根据表中信息,是否有90%的把握认为比赛的“主客场”与“胜负”之间有关?
(2)已知队与队在季后赛的总决赛中相遇,假设每场比赛结果相互独立,队除第五场比赛获胜的概率为外,其他场次比赛获胜的概率等于队常规赛60场比赛获胜的频率.记为队在总决赛中获胜的场数.
(ⅰ)求的分布列;
(ⅱ)求队获得本赛季的总冠军的概率.
附:.
() 0.100 0.050 0.025
2.706 3.841 5.024
11.直播带货是扶贫助农的一种新模式,这种模式是利用主流媒体的公信力,聚合销售主播的力量助力打通农产品产销链条,切实助力贫困地区农民脱贫增收.某贫困地区有统计数据显示,2020年该地利用网络直播形式销售农产品的销售主播年龄等级分布如图1所示,一周内使用直播销售的频率分布扇形图如图2所示.若将销售主播按照年龄分为“年轻人”(岁~岁)和“非年轻人”(岁及以下或者岁及以上)两类,将一周内使用的次数为次或次以上的称为“经常使用直播销售用户”,使用次数为次或不足次的称为“不常使用直播销售用户”,则“经常使用直播销售用户”中有是“年轻人”.
(1)现对该地相关居民进行“经常使用网络直播销售与年龄关系”的调查,采用随机抽样的方法,抽取一个容量为的样本,请你根据图表中的数据,完成列联表,并根据列联表判断是否有的把握认为经常使用网络直播销售与年龄有关?
使用直播销售情况与年龄列联表
年轻人 非年轻人 合计
经常使用直播销售用户
不常使用直播销售用户
合计
(2)某投资公司在2021年年初准备将万元投资到“销售该地区农产品”的项目上,现有两种销售方案供选择:
方案一:线下销售.根据市场调研,利用传统的线下销售,到年底可能获利,可能亏损,也可能不赔不赚,且这三种情况发生的概率分别为;
方案二:线上直播销售.根据市场调研,利用线上直播销售,到年底可能获利,可能亏损,也可能不赔不赚,且这三种情况发生的概率分别为.
针对以上两种销售方案,请你从期望和方差的角度为投资公司选择一个合理的方案,并说明理由.
参考数据:独立性检验临界值表
其中,.
【答案详解】
【题型归纳】
1.D
【详解】观察等高条形图发现与相差很大,就判断两个分类变量之量关系最强.故选:D
2.D
【详解】由等高条形图可知“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的频率不同,
所以“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响在某种程度上是不同的,但是没有的把握,所以选项D正确,
故选:D.
3.D
【详解】
A错误,根据等高条形图,喜欢和不喜欢使用手机支付的比例因性别差距很明显,所以喜欢使用手机支付与性别有关;
B错误,样本中男生喜欢使用手机支付的约为40%;
女生比男生喜欢使用手机支付的可能性大些,由于不知道男女生人数,所以不能认定女生喜欢使用手机支付的人数是否比男生多.所以C错误,D正确.
故选:D
4.【详解】(1)平均值为,
8个指标中分数为4.93的指标有3个,
故从8个指标中任选1个,指标分数为4.93的概率为;
(2)
混动版 纯电动版 合计
男 55 25 80
女 15 45 60
合计 70 70 140
由于,
所以有99.9%的把握认为喜欢哪款车型和性别有关.
5.【详解】(1)由题意知,所以,糖尿病患者共有8名,其中不常喝酒的有名,
则列联表如下:
常喝 不常喝 合计
有糖尿病
无糖尿病
合计
由表中的数据可得,
因此,有的把握认为糖尿病与喝酒有关.
(2)设两名老年人分别为、,其余四名中年人为、、、,
则所有可能出现的结果有、、、、、、、
、、、、、、、,共种,
其中事件“有一名老年人和一名中年人”包含的结果有:、、、、、、、,有种,
因此,恰好抽到一名老年人和一名中年人的概率.
6.【详解】(1)由题可得,解得.
(2)平均成绩为:,
(3)∵不及格的人数为15人,
∴抽取的总人数为,
∴比赛成绩优秀的有人,
由此可得完整的2×2列联表:
优秀 非优秀 合计
男生 10 40 50
女生 25 25 50
合计 35 65 100
.
∴没有99.9%的把握认为“比赛成绩是否优秀与性别有关”
7.【详解】(1)由可得;
由可得;由可得.
所以2×2列联表如下:
完成作业所需时间 性别 合计
男生 女生
90分钟以上 80 100 180
90分钟及以下 80 140 220
合计 160 240 400
,所以依据小概率值的独立性检验,不能认为完成作业所需时间在90分钟以上与性别有关.
(2)抽取的9人中,男生有(人),女生有(人),从这9人中选取3人进行访谈,男生人数大于女生人数的情况分为:①男生2人,女生1人;②男生3人,女生0人.
所以所求概率.
【双基达标】
1.A
【详解】由列联表中的数据计算,得,
所以有的把握认为“对能否缓解交通拥堵的认识与性别有关”.
故选:A.
2.C
【详解】因为有的把握但没有的把握认为偏爱蔬菜还是肉类与性别有关,
所以的取值范围为,因此的值可能为.
故选:C.
3.B
【详解】根据独立性检验的思想,知观测值越小,变量有关系的可信程度越小,故只有B正确.
故选:B.
4.D
【详解】根据列联表知,,又,所以,故选:
5.B
【详解】根据两个表中的等高条形图知,药物A实验显示不服药与服药时患病差异较药物B实验显示明显大,
所以药物A的预防效果优于药物B的预防效果,
故选:B.
6.C
【详解】由等高条形图可知:喜欢数学的女生和男生的比为1:3,所以抽取的男生数为24人.故选C.
7.C
【详解】对于A:物理类的学生中选择政治的比例为,
历史类的学生中选择政治的比例为,因为,故选项A不正确;
对于B:物理类的学生中选择地理的比例为,
历史类的学生中选择地理的比例,因为,故选项B不正确;
对于C和D:根据已知数据可得列联表如图:
选生物 不选生物 合计
物理类
历史类
合计
所以,所以没有以上的把握认为选择生物与选考类别有关,故选项C正确,选项D不正确,
故选:C.
8.ABD
【详解】依题意,,解得,由,解得,A正确;
,则有95%的把握认为市民性别与喜欢冰雪运动有关系,B正确;
随机对一路人进行调查,喜欢冰雪运动的频率为:,
则有65%的可能性对方喜欢冰雪运动,C不正确;
,没有99%的把握认为市民性别与喜欢冰雪运动有关系,D正确.
故选:ABD
9.30
【详解】设男生人数为,依题意可得列联表如下:
喜欢追星 不喜欢追星 总计
男生
女生
总计
若在犯错误的概率不超过的前提下认为是否喜欢追星和性别有关,
则,
由,解得,
由题知应为6的整数倍,
若在犯错误的概率不超过的前提下认为是否喜欢追星和性别有关,
则男生至少有30人,
故答案为:30.
10.【详解】(1)由已知可得持不支持态度的人中有男性人,
由等高条形图可知这个男性中年龄在周岁及以上的有人;
持不支持态度的人中有女性人,
由等高条形图可知这个女性中年龄在周岁及以上的有人;
故所求在持不支持态度的人中,周岁及以上的男女比例是.
(2)由已知可得以下列联表:
周岁以下 周岁及以上 总计
不支持
支持
总计
计算得的观测值,
所以有的把握认为年龄是否在45周岁以下与对“延迟退休年龄政策”的态度有关.
11.【详解】(1)完成的列联表如下:
低学历 高学历 合计
不了解数字人民币 150 125 275
了解数字人民币 250 275 525
合计 400 400 800
(2)根据列联表得:,
故没有的把握认为“是否了解数字人民币”与“学历高低”有关.
12.【详解】(1)根据统计图,男性关注者占比为,
女性关注者占比为,男女性别比为.
(2)根据统计图计算可得,选择游戏的关注者中,男性关注者的人数为人,女性关注者的人数为人;
选择生活的关注者中,男性关注者的人数为人,女性关注者的人数为人.
零假设性别对关注者喜欢视频上传者上传视频的类型有关.
由计算的数据可以得到下面的列联表:
男性关注者人数 女性关注者人数
游戏
生活
的观测值,
因此可以认为性别与关注者喜欢视频上传者上传视频的类型有关.
13.【详解】(1)因为男性 女性的人数比为3:2,所以男性有120人,女性有80人,
又按性别分层抽样抽取20人,所以男性抽取12人,女性抽取8人,
这其中喜欢晨跑的女性有5人,所以不喜欢晨跑的女性有3人,
所以这200人中女性喜欢晨跑的有50人,不喜欢晨跑的有30人,
如下表:
喜欢晨跑 不喜欢晨跑 合计
男性 80 40 120
女性 50 30 80
合计 130 70 200
所以,
所以没有90%的把握认为喜欢晨跑与性别有关.
(2)因为按分层抽样抽取人数,所以7人中女性3人,男性4人,
现从中抽取4人,所以女性的人数X的可能取值为0,1,2,3,
所以,
,,
所以X分布列为
X 0 1 2 3
P
所以.
【高分突破】
1.B
【详解】依题意,设男、女学生的人数都为,则男、女学生的总人数为,建立列联表如下,
喜欢网络课程 不喜欢网络课程 总计
男生
女生
总计
故,由题意可得,
所以,结合选项可知,只有B符合题意.
故选:B.
2.B
【详解】由题意得到如下列联表:
喜欢看篮球赛情况 性别 喜欢 不喜欢 总计
男
女
总计
所以.
因为有95%的把握认为喜欢看篮球赛与性别有关,所以,
即,得.
又,,为整数,所以的最小值为12.
故选:B
3.A
【详解】设男生人数为,依题意可得列联表如下:
喜欢追星 不喜欢追星 总计
男生
女生
总计
若在犯错误的概率不超过的前提下认为是否喜欢追星和性别有关,则,
由,解得,
因为为整数,
所以若在犯错误的概率不超过的前提下认为是否喜欢追星和性别有关,则男生至少有人.
故选:A
4.C
【详解】方差反映一组数据的波动大小,将一组数据中的每个数据都加上或减去同一个常数后,方差不变,故①正确;一个回归方程,变量增加1个单位时,平均减少5个单位,故②不正确;线性回归方程必过样本中心点,故③正确;根据线性回归分析中相关系数的定义:在线性回归分析中,相关系数为r,越接近于1,相关程度越大,故④不正确;对于观察值来说,越大,“x与y有关系”的可信程度越大,故⑤正确.
故选:C
5.BCD
【详解】设男生的人数为(),根据题意列出列联表如下所示:
男生 女生 总计
喜欢抖音 4n 3n 7n
不喜欢抖音 n 2n 3n
总计 5n 5n 10n
则,由于有95%的把握认为是否喜欢抖音与学生性别有关,则,即,得,∴,又,∴,结合选项知B,C,D正确,
故选:BCD.
6.45
【详解】设男生有人,则男生有人,可得列联表如下:
喜欢抖音 不喜欢抖音 总计
男生
女生
总计
若有的把握认为是否喜欢抖音和性别有关,
则,可得,
由题意可得且是的倍数,所以男生至少有人,
故答案为:.
7.①④
【详解】线性回归方程必过样本中心点,故①正确.
命题“”的否定是“” 故②错误
③相关系数r绝对值越小,表明两个变量相关性越弱,故不正确;
④在一个列联表中,由计算得,则有的把握认为这两个变量间有关系,正确.
故答案为①④.
8.【详解】(1)由题可知,从200名学生中抽取1人,这个人喜欢冰雪运动的概率为0.8,
故喜欢冰雪运动的有人,
不喜欢冰雪运动的有人,即,,,,
列联表如下:
喜欢 不喜欢 合计
男生 100 20 120
女生 60 20 80
合计 160 40 200
,
故没有90%的把握认为是否喜欢冰雪运动与性别有关;
(2)按分层抽样,设抽取女生名,男生名,,解得,,
即抽取的8人中喜欢冰雪运动的女生有3人,男生有5人,
故,1,2,3,
,,
,,
的分布列如下:
0 1 2 3
;
9.【详解】(1)由频率分布直方图,知200只小白鼠按指标值分布为:
在内有(只);
在内有(只);
在内有(只);
在内有(只);
在内有(只).
由题意,有抗体且指标值小于60的有50只;而指标值小于60的小白鼠共有(只),所以指标值小于60且没有抗体的小白鼠有20只,同理,指标值不小于60且没有抗体的小白鼠有20只,故列联表如下:
单位:只
抗体 指标值 合计
小于60 不小于60
有抗体 50 110 160
没有抗体 20 20 40
合计 70 130 200
零假设为:注射疫苗后小白鼠产生抗体与指标值不小于60无关联.
根据列联表中数据,得.
根据的独立性检验,推断不成立,即认为注射疫苗后小白鼠产生抗体与指标值不小于60有关,此推断犯错误的概率不大于0.05.
(2)(i)令事件“小白鼠第一次注射疫苗产生抗体”,事件“小白鼠第二次注射疫苗产生抗体”,事件“小白鼠注射2次疫苗后产生抗体”.
记事件A,B,C发生的概率分别为,,,
则,,.
所以一只小白鼠注射2次疫苗后产生抗体的概率.
(ii)由题意,知随机变量,().
因为最大,
所以,
解得,因为是整数,所以或,所以接受接种试验的人数为99或100.
①当接种人数为99时,;
②当接种人数为100时,.
10.【详解】(1)根据表格信息得到列联表:
队胜 队负 合计
主场 25 5 30
客场 20 10 30
合计 45 15 60
所以没有90%的把握认为比赛的“主客场”与“胜负”之间有关.
(2)(ⅰ)的所有可能取值为0,1,2,3,
队前4场中每场获胜的概率为.
;
;
;
.
所以的分布列为
0 1 2 3
(ⅱ)队获得本赛季的总冠军的概率为
.
11.【详解】(1)由图1知,“年轻人”占比为,即有(人),“非年轻人”有(人)
由图2知,“经常使用直播销售用户”占比为,即有(人),“不常使用直播销售用户” 有(人).
“经常使用直播销售用户的年轻人”有中有(人),“经常使用直播销售用户的非年轻人”有(人)
补全的列联表如下:
年轻人 非年轻人 合计
经常使用直播销售用户
不常使用直播销售用户
合计
于是.
,
即有的把握认为经常使用网络直播销售与年龄有关.
(2)若按方案一,设获利万元,则可取的值为行,的分布列为:
(万元),
若按方案二,设获利万元,则可取的值为,的分布列为:
(万元),
,
由方案二的方差要比方案一的方差大得多,从稳定性方面看方案一线下销售更稳妥,故选方案一.
【知识梳理】
知识点一 分类变量
为了表述方便,我们经常会使用一种特殊的随机变量,以区别不同的现象或性质,这类随机变量称为分类变量.
分类变量的取值可以用实数表示.
知识点二 2×2列联表
1.2×2列联表给出了成对分类变量数据的交叉分类频数.
2.定义一对分类变量X和Y,我们整理数据如下表所示:
X Y 合计
Y=0 Y=1
X=0 a b a+b
X=1 c d c+d
合计 a+c b+d n=a+b+c+d
像这种形式的数据统计表称为2×2列联表.
知识点三 独立性检验
1.定义:利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2独立性检验,读作“卡方独立性检验”.简称独立性检验.
2.χ2=,其中n=a+b+c+d.
3.独立性检验解决实际问题的主要环节
(1)提出零假设H0:X和Y相互独立,并给出在问题中的解释.
(2)根据抽样数据整理出2×2列联表,计算χ2的值,并与临界值xα比较.
(3)根据检验规则得出推断结论.
(4)在X和Y不独立的情况下,根据需要,通过比较相应的频率,分析X和Y间的影响规律.
【题型归纳】
一、等高堆积条形图的应用
1.观察下列各图,其中两个分类变量x,y之间关系最强的是( )
A. B.
C. D.
2.下面的等高条形图可以说明的问题是( )
A.“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响是绝对不同的
B.“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响没有什么不同
C.此等高条形图看不出两种手术有什么不同的地方
D.“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响在某种程度上是不同的,但是没有的把握
3.为了了解某高校学生喜欢使用手机支付是否与性别有关,抽取了部分学生作为样本,统计后作出如图所示的等高条形图,则下列说法正确的是( )
A.喜欢使用手机支付与性别无关
B.样本中男生喜欢使用手机支付的约
C.样本中女生喜欢使用手机支付的人数比男生多
D.女生比男生喜欢使用手机支付的可能性大些
二、由χ2进行独立性检验
命题角度1 有关“相关的检验”
4.在2021年的一次车展上,某国产汽车厂家的一个品牌推出了1.5升混动版和纯电动版两款车型,自这两款车型上市后,便获得了不错的口碑,汽车测评人老李通过自媒体平台,分8个指标对这两款车型进行了综合评测打分(满分:5分),如图所示:
(1)求综合评测分数的平均值;从上图8个指标中任选1个,求指标分数为4.93的概率;
(2)老李对两款车型的车主的性别作了统计,得到数据如下2×2列联表:
混动版 纯电动版 合计
男 25
女 15 60
合计 70
请将上述列联表补充完整,并判断是否有99.9%的把握认为喜欢哪款车型和性别有关.
附:,其中.
0.10 0.050 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
5.某科研机构为了研究喝酒与糖尿病是否有关,对该市名成年男性进行了问卷调查,并得到了如下列联表,规定“”平均每天喝以上的”为常喝.已知在所有的人中随机抽取人,患糖尿病的概率为.
常喝 不常喝 合计
有糖尿病
无糖尿病
合计
(1)请将上表补充完整,并判断是否有的把握认为糖尿病与喝酒有关?请说明理由;
(2)已知常喝酒且有糖尿病的人中恰有两名老年人,其余为中年人,现从常喝酒且有糖尿病的这人中随机抽取人,求恰好抽到一名老年人和一名中年人的概率.
参考公式及数据:,.
命题角度2 有关“无关的检验”
6.某校开展党史知识竞赛.现从参加竞赛活动的学生中随机抽取了n名学生,将他们的比赛成绩(满分为100分)分为6组:,,,,,得到如图所示的频率分布直方图.
(1)求a的值;
(2)估计这n名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(3)活动规定:竞赛成绩位于60分以下为不及格,不低于80分为“优秀”,若抽取的学生中成绩不及格的有15人.请将下面的2×2列联表补充完整,并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 不优秀 合计
男生 40
女生 50
合计
参考公式及数据:,.
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
7.2021年1月以来,教育部相继出台文件,对中小学生手机、睡眠、读物、作业、体质管理作出规定.为了在“控量”的同时力求“增效”,提高作业质量,某学校计划设计差异化作业.因此该校对初三年级的400名学生每天完成作业所需时间进行统计,部分数据如下表:
单位:人
完成作业所需时间 性别 合计
男生 女生
90分钟以上 80 x 180
90分钟及以下 y z 220
合计 160 240 400
(1)求x,y,z的值,并根据题中的列联表,依据小概率值的独立性检验,判断是否可以认为完成作业所需时间在90分钟以上与性别有关;
(2)学校从完成作业所需时间在90分钟以上的学生中用分层随机抽样的方法抽取9人了解情况,甲老师再从这9人中选取3人进行访谈,求甲老师选取的3人中男生人数大于女生人数的概率.
附:
0.1 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
参考公式:,.
【双基达标】
1.某省二线城市地铁正式开工建设,地铁时代的到来能否缓解该市的交通拥堵状况呢 某社团进行社会调查,得到的数据如下表:
男性市民 女性市民
认为能缓解交通拥堵
认为不能缓解交通拥堵
则下列结论中正确的是( )A.有的把握认为“对能否缓解交通拥堵的认识与性别有关”
B.有的把握认为“对能否缓解交通拥堵的认识与性别无关”
C.有的把握认为“对能否缓解交通拥堵的认识与性别有关”
D.有的把握认为“对能否缓解交通拥堵的认识与性别无关”
2.某学校食堂对高三学生偏爱蔬菜还是肉类与性别的关系进行了一次调查,根据独立性检验原理,处理所得数据之后发现,有的把握但没有的把握认为偏爱蔬菜还是肉类与性别有关,则的值可能为( )
附表:
A. B.
C. D.
3.在利用统计量来判断两个变量与之间是否有关系时,下列说法正确的是( )
A.越大,“与有关系”的可信程度越小
B.越小,“与有关系”的可信程度越小
C.越接近于0,“与没有关系”的可信程度越小
D.越大,“与没有关系”的可信程度越大
4.假设有两个变量X和Y,他们的取值分别为,和,,其列联表为:
总计
21 73
8 25 33
总计 46 106
则表中,的值分别是( )
A.94,96 B.54,52 C.52,50 D.52,60
5.为考查A,B两种药物预防某疾病的效果,进行动物实验,分别得到如下等高条形图:根据图中信息,在下列各项中,说法最佳的一项是( )
A.药物B的预防效果优于药物A的预防效果
B.药物A的预防效果优于药物B的预防效果
C.药物A,B对该疾病均有显著的预防效果
D.药物A,B对该疾病均没有预防效果
6.如图是调查某学校高三年级男女学生是否喜欢数学的等高条形图,阴影部分的高表示喜欢数学的频率.已知该年级男生女生各500名(所有学生都参加了调查),现从所有喜欢数学的同学中按分层抽样的方式抽取32人,则抽取的男生人数为
A.16 B.32 C.24 D.8
7.2021年河北省采用“”新高考模式,其中“3”为全国统考科目语文 数学和外语;“1”为考生在物理和历史中选择一门;“2”为考生在思想政治 地理 化学和生物四门中再选择两门.某中学调查了高一年级学生的选科倾向,随机抽取人,其中选考物理的人,选考历史的人,统计各选科人数如下表,则下列说法正确的是( )
选择科目选考类别 思想政治 地理 化学 生物
物理类 80 100 145 115
历史类 50 45 30 35
附:
0.10 0.05 0.025 0.010 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
A.物理类的学生中选择政治的比例比历史类的学生中选择政治的比例高
B.物理类的学生中选择地理的比例比历史类的学生中选择地理的比例高
C.没有以上的把握认为选择生物与选考类别有关
D.有以上的把握认为选择生物与选考类别有关
8.(多选)北京冬奥会临近开幕,大众对冰雪运动关注不断上升,各地陆续建成众多冰雪设施,广大市民有条件体验冰雪活动的乐趣,为研究市民性别和喜欢冰雪活动是否有关,某校社团学生在部分市民中进行了一次调查,得到下表:
冰雪运动的喜好 性别 合计
男性 女性
喜欢 140 m 140+m
不喜欢 n 80 80+n
合计 140+n 80+m 220+m+n
已知男性喜欢冰雪运动的人数占男性人数的,女性喜欢冰雪运动的人数占女性人数的,则( )
参考:,P(>3.841)=0.05,P(>6.635)=0.01.
A.列联表中n的值为60,m的值为120
B.有95%的把握认为市民性别和喜欢冰雪运动有关系
C.随机对一路人进行调查,有95%的可能性对方喜欢冰雪运动
D.没有99%的把握认为市民性别和喜欢冰雪运动有关系
9.针对“中学生追星问题”,某校团委对“学生性别和中学生追星是否有关”作了一次调查,其中女生人数是男生人数的,男生追星的人数占男生人数的,女生追星的人数占女生人数的,若有的把握认为中学生追星与性别有关,则男生至少有__________人.
参考数据及公式如下:
0.050 0.010 0.001
3.841 6.635 10.828
,.
10.某部门为了解人们对“延迟退休年龄政策”的支持度,随机调查了人,其中男性人.调查发现持不支持态度的有人,其中男性占.分析这个持不支持态度的样本的年龄和性别结构,绘制等高条形图如图所示.
(1)在持不支持态度的人中,周岁及以上的男女比例是多少?
(2)调查数据显示,个持支持态度的人中有人年龄在周岁以下.填写下面的列联表,问能否有的把握认为年龄是否在周岁以下与对“延迟退休年龄政策”的态度有关.
参考公式及数据:,.
11.数字人民币是由中国人民银行发行的数字形式的法定货币,由指定运营机构参与运营并向公众兑换,与纸钞和硬币等价.为了进一步了解普通大众对数字人民币的认知情况,某机构进行了一次问卷调查,统计结果如下:
小学及以下 初中 高中 大学专科 大学本科 硕士研究生及以上
不了解数字人民币 35 35 80 55 64 6
了解数字人民币 40 60 150 110 140 25
(1)如果将高中及以下学历称为“低学历”,大学专科及以上学历称为“高学历”,根据所给数据,完成下面的列联表;
低学历 高学历 合计
不了解数字人民币
了解数字人民币
合计 800
(2)根据(1)中所得列联表,判断是否有的把握认为“是否了解数字人民币”与“学历高低”有关?
附:,其中.
0.050 0.010 0.001
K 3.841 6.635 10.828
12.某视频上传者为确定下一段时间的视频制作方向,在动态中发布投票,投票主题为“你希望我接下来更新哪个方向的视频”,共计人参与此投票,投票结果如下图所示(每位关注者仅选一项).
其中,投票游戏、动漫、生活的关注者之比为.
(1)求参与投票的关注者的性别比;
(2)以游戏与生活两个方向为例,依据小概率值的独立性检验,判断性别与关注者喜欢视频上传者上传视频的类型是否有关.
注:;临界值,.
13.晨跑是不少青年爱好者锻炼身体的一种运动方式,某机构随机抽取了某社区200名青年进行问卷调查,其中男性与女性的人数比为3:2,得到如下的列联表,
喜欢晨跑 不喜欢晨跑 合计
男性 40
女性
合计
现从这200名青年中按性别用分层抽样的方法随机抽取20人,其中喜欢晨跑的女性有5人.
(1)完成表中数据并判断是否有90%的把握认为喜欢晨跑与性别有关;
(2)从上述样本中不喜欢晨跑的青年中用分层抽样的方法任取7名,再从这7人中抽取4人调查,其中这4人中的女性人数为X,求X的分布列及数学期望.
参考公式及数据:,其中.
0.10 0.05 0.01 0.005 0.001
2.706 3.841 6.635 7.879 10.828
【高分突破】
1.2020年2月,全国掀起了“停课不停学”的热潮,各地教师通过网络直播 微课推送等多种方式来指导学生线上学习.为了调查学生对网络课程的热爱程度,研究人员随机调查了相同数量的男 女学生,发现有80%的男生喜欢网络课程,有40%的女生不喜欢网络课程,且有99%的把握但没有99.9%的把握认为是否喜欢网络课程与性别有关,则被调查的男 女学生总数量可能为( )
附:,其中.
0.1 0.05 0.01 0.001
2.706 3.841 6.635 10.828
A.130 B.190 C.240 D.250
2.某大学为了解喜欢看篮球赛是否与性别有关,随机调查了部分学生,在被调查的学生中,男生人数是女生人数的2倍,男生喜欢看篮球赛的人数占男生人数的,女生喜欢看篮球赛的人数占女生人数的.若被调查的男生人数为,且有95%的把握认为喜欢看篮球赛与性别有关,则的最小值为( )
A.6 B.12 C.18 D.36
3.针对“中学生追星问题”,某校团委对“学生性别和中学生追星是否有关”作了一次调查,调查样本中女生人数是男生人数的,男生追星的人数占男生人数的,女生追星的人数占女生人数的,若有的把握认为是否追星和性别有关,则调查样本中男生至少有( )
参考数据及公式如下:
A.12人 B.11人 C.10人 D.18人
4.以下说法:
①将一组数据中的每一个数据都加上或减去同一个常数后,方差不变;
②设有一个回归方程,变量增加1个单位时,平均增加5个单位
③线性回归方程必过
④设具有相关关系的两个变量的相关系数为,那么越接近于0,之间的线性相关程度越高;
⑤在一个列联表中,由计算得的值,那么的值越大,判断两个变量间有关联的把握就越大。
其中错误的个数是( )
A.0 B.1 C.2 D.3
5.(多选)针对时下的“抖音热”,某校团委对“是否喜欢抖音与学生性别的关系”进行了一次调查,其中被调查的男、女生人数相同,男生中喜欢抖音的人数占男生人数的,女生中喜欢抖音的人数占女生人数的,若有95%的把握认为是否喜欢抖音与学生性别有关,则被调查的学生中男生的人数可能为( )
A.25 B.45
C.60 D.75
6.针对时下的“抖音热”,某校团委对“学生性别和喜欢抖音是否有关”作了一次调查,其中被调查的男女生人数相同,男生喜欢抖音的人数占男生人数的,女生喜欢抖音的人数占女生人数.若有的把握认为是否喜欢抖音和性别有关,则调查人数中男生至少有________人.
7.下列说法:
①线性回归方程必过;
②命题“”的否定是“”
③相关系数越小,表明两个变量相关性越弱;
④在一个列联表中,由计算得,则有的把握认为这两个变量间有关系;
其中正确的说法是__________.(把你认为正确的结论都写在横线上)
本题可参考独立性检验临界值表:
8.2022年是奥运会,我国北京和张家口联合承办第二十四届冬季奥运会,本届冬奥会共设7个大项(滑雪、滑冰、冰球、冰壶、雪车、雪橇、冬季两项)、15个分项(高山滑雪、自由式滑雪、单板滑雪、跳台滑雪、越野滑雪、北欧两项、短道速滑、速度滑冰、花样滑冰、冰球、冰壶、雪车、钢架雪车、雪橇、冬季两项)共计109个小项.某校为了调查学生是否喜欢冬季冰雪运动与性别有关,在高三年级特选取了200名学生进行了问卷调查,得到如下的列联表:
喜欢 不喜欢 合计
男生
女生
合计
已知从这200名学生中随机抽取1人,这个人喜欢冰雪运动的概率为0.8,表格中,.
(1)完成列联表,并判断是否有90%的把握认为喜欢冰雪运动与性别有关;
(2)从上述喜欢冰雪运动的学生中用分层抽样的方法抽取8名学生,再从这8人中抽取3人调查其喜欢的运动,用表示3人中女生的人数,求的分布列及数学期望.
参考公式及数据:,其中.
0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.01 0.005 0.001
0.46 0.71 1.32 2.07 2.71 3.84 5.024 6.635 7.879 10.828
9.为了检测某种抗病毒疫苗的免疫效果,需要进行动物与人体试验.研究人员将疫苗注射到200只小白鼠体内,一段时间后测量小白鼠的某项指标值,按,,,,分组,绘制频率分布直方图如图所示.试验发现小白鼠体内产生抗体的共有160只,其中该项指标值不小于60的有110只.假设小白鼠注射疫苗后是否产生抗体相互独立.
(1)填写下面的列联表,并根据列联表及的独立性检验,判断能否认为注射疫苗后小白鼠产生抗体与指标值不小于60有关.
单位:只
抗体 指标值 合计
小于60 不小于60
有抗体
没有抗体
合计
(2)为检验疫苗二次接种的免疫抗体性,对第一次注射疫苗后没有产生抗体的40只小白鼠进行第二次注射疫苗,结果又有20只小白鼠产生抗体.
(i)用频率估计概率,求一只小白鼠注射2次疫苗后产生抗体的概率;
(ii)以(i)中确定的概率作为人体注射2次疫苗后产生抗体的概率,进行人体接种试验,记个人注射2次疫苗后产生抗体的数量为随机变量.试验后统计数据显示,当时,取最大值,求参加人体接种试验的人数及.
参考公式: (其中为样本容量)
参考数据:
0.50 0.40 0.25 0.15 0.100 0.050 0.025
0.455 0.708 1.323 2.072 2.706 3.841 5.024
10.中国职业篮球联赛(CBA联赛)分为常规赛和季后赛.由于新冠疫情关系,今年联赛采用赛会制:所有球队集中在同一个地方比赛,分两个阶段进行,每个阶段采用循环赛,分主场比赛和客场比赛,积分排名前8的球队进入季后赛.季后赛的总决赛采用五场三胜制(“五场三胜制”是指在五场比赛中先胜三场者获得比赛胜利,胜者成为本赛季的总冠军).下表是队在常规赛60场比赛中的比赛结果记录表.
阶段 比赛场数 主场场数 获胜场数 主场获胜场数
第一阶段 30 15 20 10
第二阶段 30 15 25 15
(1)根据表中信息,是否有90%的把握认为比赛的“主客场”与“胜负”之间有关?
(2)已知队与队在季后赛的总决赛中相遇,假设每场比赛结果相互独立,队除第五场比赛获胜的概率为外,其他场次比赛获胜的概率等于队常规赛60场比赛获胜的频率.记为队在总决赛中获胜的场数.
(ⅰ)求的分布列;
(ⅱ)求队获得本赛季的总冠军的概率.
附:.
() 0.100 0.050 0.025
2.706 3.841 5.024
11.直播带货是扶贫助农的一种新模式,这种模式是利用主流媒体的公信力,聚合销售主播的力量助力打通农产品产销链条,切实助力贫困地区农民脱贫增收.某贫困地区有统计数据显示,2020年该地利用网络直播形式销售农产品的销售主播年龄等级分布如图1所示,一周内使用直播销售的频率分布扇形图如图2所示.若将销售主播按照年龄分为“年轻人”(岁~岁)和“非年轻人”(岁及以下或者岁及以上)两类,将一周内使用的次数为次或次以上的称为“经常使用直播销售用户”,使用次数为次或不足次的称为“不常使用直播销售用户”,则“经常使用直播销售用户”中有是“年轻人”.
(1)现对该地相关居民进行“经常使用网络直播销售与年龄关系”的调查,采用随机抽样的方法,抽取一个容量为的样本,请你根据图表中的数据,完成列联表,并根据列联表判断是否有的把握认为经常使用网络直播销售与年龄有关?
使用直播销售情况与年龄列联表
年轻人 非年轻人 合计
经常使用直播销售用户
不常使用直播销售用户
合计
(2)某投资公司在2021年年初准备将万元投资到“销售该地区农产品”的项目上,现有两种销售方案供选择:
方案一:线下销售.根据市场调研,利用传统的线下销售,到年底可能获利,可能亏损,也可能不赔不赚,且这三种情况发生的概率分别为;
方案二:线上直播销售.根据市场调研,利用线上直播销售,到年底可能获利,可能亏损,也可能不赔不赚,且这三种情况发生的概率分别为.
针对以上两种销售方案,请你从期望和方差的角度为投资公司选择一个合理的方案,并说明理由.
参考数据:独立性检验临界值表
其中,.
【答案详解】
【题型归纳】
1.D
【详解】观察等高条形图发现与相差很大,就判断两个分类变量之量关系最强.故选:D
2.D
【详解】由等高条形图可知“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的频率不同,
所以“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响在某种程度上是不同的,但是没有的把握,所以选项D正确,
故选:D.
3.D
【详解】
A错误,根据等高条形图,喜欢和不喜欢使用手机支付的比例因性别差距很明显,所以喜欢使用手机支付与性别有关;
B错误,样本中男生喜欢使用手机支付的约为40%;
女生比男生喜欢使用手机支付的可能性大些,由于不知道男女生人数,所以不能认定女生喜欢使用手机支付的人数是否比男生多.所以C错误,D正确.
故选:D
4.【详解】(1)平均值为,
8个指标中分数为4.93的指标有3个,
故从8个指标中任选1个,指标分数为4.93的概率为;
(2)
混动版 纯电动版 合计
男 55 25 80
女 15 45 60
合计 70 70 140
由于,
所以有99.9%的把握认为喜欢哪款车型和性别有关.
5.【详解】(1)由题意知,所以,糖尿病患者共有8名,其中不常喝酒的有名,
则列联表如下:
常喝 不常喝 合计
有糖尿病
无糖尿病
合计
由表中的数据可得,
因此,有的把握认为糖尿病与喝酒有关.
(2)设两名老年人分别为、,其余四名中年人为、、、,
则所有可能出现的结果有、、、、、、、
、、、、、、、,共种,
其中事件“有一名老年人和一名中年人”包含的结果有:、、、、、、、,有种,
因此,恰好抽到一名老年人和一名中年人的概率.
6.【详解】(1)由题可得,解得.
(2)平均成绩为:,
(3)∵不及格的人数为15人,
∴抽取的总人数为,
∴比赛成绩优秀的有人,
由此可得完整的2×2列联表:
优秀 非优秀 合计
男生 10 40 50
女生 25 25 50
合计 35 65 100
.
∴没有99.9%的把握认为“比赛成绩是否优秀与性别有关”
7.【详解】(1)由可得;
由可得;由可得.
所以2×2列联表如下:
完成作业所需时间 性别 合计
男生 女生
90分钟以上 80 100 180
90分钟及以下 80 140 220
合计 160 240 400
,所以依据小概率值的独立性检验,不能认为完成作业所需时间在90分钟以上与性别有关.
(2)抽取的9人中,男生有(人),女生有(人),从这9人中选取3人进行访谈,男生人数大于女生人数的情况分为:①男生2人,女生1人;②男生3人,女生0人.
所以所求概率.
【双基达标】
1.A
【详解】由列联表中的数据计算,得,
所以有的把握认为“对能否缓解交通拥堵的认识与性别有关”.
故选:A.
2.C
【详解】因为有的把握但没有的把握认为偏爱蔬菜还是肉类与性别有关,
所以的取值范围为,因此的值可能为.
故选:C.
3.B
【详解】根据独立性检验的思想,知观测值越小,变量有关系的可信程度越小,故只有B正确.
故选:B.
4.D
【详解】根据列联表知,,又,所以,故选:
5.B
【详解】根据两个表中的等高条形图知,药物A实验显示不服药与服药时患病差异较药物B实验显示明显大,
所以药物A的预防效果优于药物B的预防效果,
故选:B.
6.C
【详解】由等高条形图可知:喜欢数学的女生和男生的比为1:3,所以抽取的男生数为24人.故选C.
7.C
【详解】对于A:物理类的学生中选择政治的比例为,
历史类的学生中选择政治的比例为,因为,故选项A不正确;
对于B:物理类的学生中选择地理的比例为,
历史类的学生中选择地理的比例,因为,故选项B不正确;
对于C和D:根据已知数据可得列联表如图:
选生物 不选生物 合计
物理类
历史类
合计
所以,所以没有以上的把握认为选择生物与选考类别有关,故选项C正确,选项D不正确,
故选:C.
8.ABD
【详解】依题意,,解得,由,解得,A正确;
,则有95%的把握认为市民性别与喜欢冰雪运动有关系,B正确;
随机对一路人进行调查,喜欢冰雪运动的频率为:,
则有65%的可能性对方喜欢冰雪运动,C不正确;
,没有99%的把握认为市民性别与喜欢冰雪运动有关系,D正确.
故选:ABD
9.30
【详解】设男生人数为,依题意可得列联表如下:
喜欢追星 不喜欢追星 总计
男生
女生
总计
若在犯错误的概率不超过的前提下认为是否喜欢追星和性别有关,
则,
由,解得,
由题知应为6的整数倍,
若在犯错误的概率不超过的前提下认为是否喜欢追星和性别有关,
则男生至少有30人,
故答案为:30.
10.【详解】(1)由已知可得持不支持态度的人中有男性人,
由等高条形图可知这个男性中年龄在周岁及以上的有人;
持不支持态度的人中有女性人,
由等高条形图可知这个女性中年龄在周岁及以上的有人;
故所求在持不支持态度的人中,周岁及以上的男女比例是.
(2)由已知可得以下列联表:
周岁以下 周岁及以上 总计
不支持
支持
总计
计算得的观测值,
所以有的把握认为年龄是否在45周岁以下与对“延迟退休年龄政策”的态度有关.
11.【详解】(1)完成的列联表如下:
低学历 高学历 合计
不了解数字人民币 150 125 275
了解数字人民币 250 275 525
合计 400 400 800
(2)根据列联表得:,
故没有的把握认为“是否了解数字人民币”与“学历高低”有关.
12.【详解】(1)根据统计图,男性关注者占比为,
女性关注者占比为,男女性别比为.
(2)根据统计图计算可得,选择游戏的关注者中,男性关注者的人数为人,女性关注者的人数为人;
选择生活的关注者中,男性关注者的人数为人,女性关注者的人数为人.
零假设性别对关注者喜欢视频上传者上传视频的类型有关.
由计算的数据可以得到下面的列联表:
男性关注者人数 女性关注者人数
游戏
生活
的观测值,
因此可以认为性别与关注者喜欢视频上传者上传视频的类型有关.
13.【详解】(1)因为男性 女性的人数比为3:2,所以男性有120人,女性有80人,
又按性别分层抽样抽取20人,所以男性抽取12人,女性抽取8人,
这其中喜欢晨跑的女性有5人,所以不喜欢晨跑的女性有3人,
所以这200人中女性喜欢晨跑的有50人,不喜欢晨跑的有30人,
如下表:
喜欢晨跑 不喜欢晨跑 合计
男性 80 40 120
女性 50 30 80
合计 130 70 200
所以,
所以没有90%的把握认为喜欢晨跑与性别有关.
(2)因为按分层抽样抽取人数,所以7人中女性3人,男性4人,
现从中抽取4人,所以女性的人数X的可能取值为0,1,2,3,
所以,
,,
所以X分布列为
X 0 1 2 3
P
所以.
【高分突破】
1.B
【详解】依题意,设男、女学生的人数都为,则男、女学生的总人数为,建立列联表如下,
喜欢网络课程 不喜欢网络课程 总计
男生
女生
总计
故,由题意可得,
所以,结合选项可知,只有B符合题意.
故选:B.
2.B
【详解】由题意得到如下列联表:
喜欢看篮球赛情况 性别 喜欢 不喜欢 总计
男
女
总计
所以.
因为有95%的把握认为喜欢看篮球赛与性别有关,所以,
即,得.
又,,为整数,所以的最小值为12.
故选:B
3.A
【详解】设男生人数为,依题意可得列联表如下:
喜欢追星 不喜欢追星 总计
男生
女生
总计
若在犯错误的概率不超过的前提下认为是否喜欢追星和性别有关,则,
由,解得,
因为为整数,
所以若在犯错误的概率不超过的前提下认为是否喜欢追星和性别有关,则男生至少有人.
故选:A
4.C
【详解】方差反映一组数据的波动大小,将一组数据中的每个数据都加上或减去同一个常数后,方差不变,故①正确;一个回归方程,变量增加1个单位时,平均减少5个单位,故②不正确;线性回归方程必过样本中心点,故③正确;根据线性回归分析中相关系数的定义:在线性回归分析中,相关系数为r,越接近于1,相关程度越大,故④不正确;对于观察值来说,越大,“x与y有关系”的可信程度越大,故⑤正确.
故选:C
5.BCD
【详解】设男生的人数为(),根据题意列出列联表如下所示:
男生 女生 总计
喜欢抖音 4n 3n 7n
不喜欢抖音 n 2n 3n
总计 5n 5n 10n
则,由于有95%的把握认为是否喜欢抖音与学生性别有关,则,即,得,∴,又,∴,结合选项知B,C,D正确,
故选:BCD.
6.45
【详解】设男生有人,则男生有人,可得列联表如下:
喜欢抖音 不喜欢抖音 总计
男生
女生
总计
若有的把握认为是否喜欢抖音和性别有关,
则,可得,
由题意可得且是的倍数,所以男生至少有人,
故答案为:.
7.①④
【详解】线性回归方程必过样本中心点,故①正确.
命题“”的否定是“” 故②错误
③相关系数r绝对值越小,表明两个变量相关性越弱,故不正确;
④在一个列联表中,由计算得,则有的把握认为这两个变量间有关系,正确.
故答案为①④.
8.【详解】(1)由题可知,从200名学生中抽取1人,这个人喜欢冰雪运动的概率为0.8,
故喜欢冰雪运动的有人,
不喜欢冰雪运动的有人,即,,,,
列联表如下:
喜欢 不喜欢 合计
男生 100 20 120
女生 60 20 80
合计 160 40 200
,
故没有90%的把握认为是否喜欢冰雪运动与性别有关;
(2)按分层抽样,设抽取女生名,男生名,,解得,,
即抽取的8人中喜欢冰雪运动的女生有3人,男生有5人,
故,1,2,3,
,,
,,
的分布列如下:
0 1 2 3
;
9.【详解】(1)由频率分布直方图,知200只小白鼠按指标值分布为:
在内有(只);
在内有(只);
在内有(只);
在内有(只);
在内有(只).
由题意,有抗体且指标值小于60的有50只;而指标值小于60的小白鼠共有(只),所以指标值小于60且没有抗体的小白鼠有20只,同理,指标值不小于60且没有抗体的小白鼠有20只,故列联表如下:
单位:只
抗体 指标值 合计
小于60 不小于60
有抗体 50 110 160
没有抗体 20 20 40
合计 70 130 200
零假设为:注射疫苗后小白鼠产生抗体与指标值不小于60无关联.
根据列联表中数据,得.
根据的独立性检验,推断不成立,即认为注射疫苗后小白鼠产生抗体与指标值不小于60有关,此推断犯错误的概率不大于0.05.
(2)(i)令事件“小白鼠第一次注射疫苗产生抗体”,事件“小白鼠第二次注射疫苗产生抗体”,事件“小白鼠注射2次疫苗后产生抗体”.
记事件A,B,C发生的概率分别为,,,
则,,.
所以一只小白鼠注射2次疫苗后产生抗体的概率.
(ii)由题意,知随机变量,().
因为最大,
所以,
解得,因为是整数,所以或,所以接受接种试验的人数为99或100.
①当接种人数为99时,;
②当接种人数为100时,.
10.【详解】(1)根据表格信息得到列联表:
队胜 队负 合计
主场 25 5 30
客场 20 10 30
合计 45 15 60
所以没有90%的把握认为比赛的“主客场”与“胜负”之间有关.
(2)(ⅰ)的所有可能取值为0,1,2,3,
队前4场中每场获胜的概率为.
;
;
;
.
所以的分布列为
0 1 2 3
(ⅱ)队获得本赛季的总冠军的概率为
.
11.【详解】(1)由图1知,“年轻人”占比为,即有(人),“非年轻人”有(人)
由图2知,“经常使用直播销售用户”占比为,即有(人),“不常使用直播销售用户” 有(人).
“经常使用直播销售用户的年轻人”有中有(人),“经常使用直播销售用户的非年轻人”有(人)
补全的列联表如下:
年轻人 非年轻人 合计
经常使用直播销售用户
不常使用直播销售用户
合计
于是.
,
即有的把握认为经常使用网络直播销售与年龄有关.
(2)若按方案一,设获利万元,则可取的值为行,的分布列为:
(万元),
若按方案二,设获利万元,则可取的值为,的分布列为:
(万元),
,
由方案二的方差要比方案一的方差大得多,从稳定性方面看方案一线下销售更稳妥,故选方案一.
