第七章《随机变量及其分布》同步单元 高分突破必刷卷(培优版)(Word版含答案)
文档属性
| 名称 | 第七章《随机变量及其分布》同步单元 高分突破必刷卷(培优版)(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 831.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 11:39:31 | ||
图片预览




文档简介
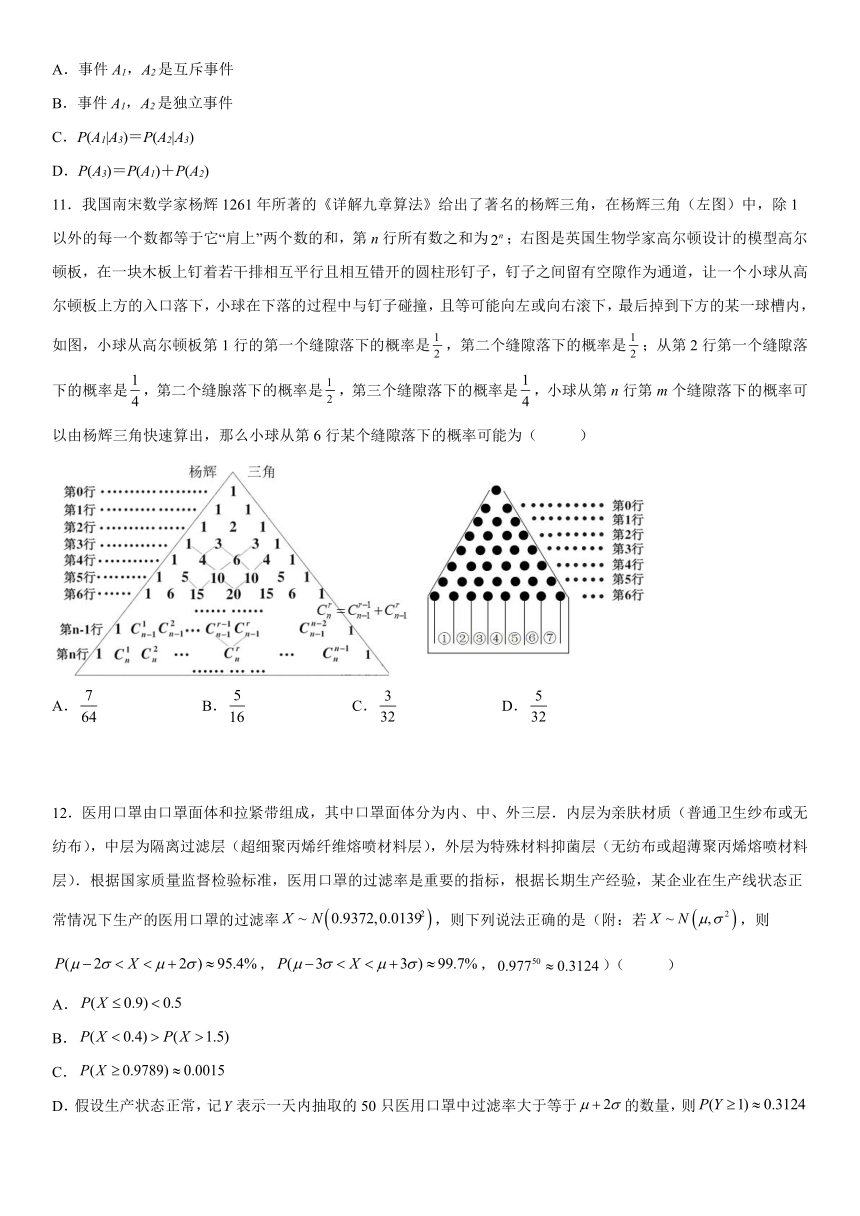
第七章《随机变量及其分布》同步单元高分突破必刷卷(培优版)
(时间:120分钟 满分:150分)
单项选择题(本大题共8小题,每小题5分,共40分)
1.袋子中装有大小、形状完全相同的2个白球和2个红球,现从中不放回地摸取两个球,已知第一次摸到的是红球,则第二次摸到白球的概率为( )
A. B. C. D.
2.已知随机变量满足,且随机变量的分布列如下:
0 1 2
则随机变量的方差( )A. B. C. D.
3.某种品牌摄像头的使用寿命(单位:年)服从正态分布,且使用寿命不少于2年的概率为0.8,使用寿命不少于6年的概率为0.2.某校在大门口同时安装了两个该种品牌的摄像头,则在4年内这两个摄像头都能正常工作的概率为( )
A.0.2 B.0.25
C.0.4 D.0.8
4.某无人机配件厂商从其所生产的某种无人机配件中随机抽取了一部分进行质量检测,其某项质量测试指标值X服从正态分布,且落在区间内的无人机配件个数为则可估计所抽取的这批无人机配件中质量指标值低于的个数大约为( )
(附:若随机变量服从正态分布,则
A. B. C. D.
5.已知随机变量X,Y,Z满足X~N(3,),Y~N(1,),Z=Y-1,且P(X>4)=0.1,则P(Z2<1)的值为( )
A.0.1 B.0.2
C.0.8 D.0.9
6.已知随机变量的分布列如表所示:
0 1
其中.若对所有都成立,则的取值范围为( )
A. B. C. D.
7.随机变量的分布列如下表所示,若,则
-1 0 1
A.4 B.5 C.6 D.7
8.为喜迎“中国共产党建党100华诞”,某中学高二年级历史方向类的班级举行“党史知识”竞赛.在本次竞赛中共有40道选择题,每道选择题都有4个选项,其中有且只有一个选项是正确的.评分标准规定:“每题只选一个选项,答对得5分,不答或答错倒扣2分”.某学生每道题答对的概率都为,则该学生在本次竞赛时得分的均值为( )
A.36 B.32 C.172 D.144
多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.一个袋子中装有除颜色外完全相同的5个球.,其中有3个红球,2个白球,每次从中随机摸出1个球,则下列结论中正确的是( )
A.若不放回的摸球2次,则第一次摸到红球的概率为
B.若不放回的摸球2次,则在第一次摸到红球的条件下第二次摸到红球的概率为
C.若有放回的摸球3次,仅有前2次摸到红球的概率为
D.若有放回的摸球3次,则恰有2次摸到红球的概率为
10.如图所示,是一个3×3九宫格,现从这9个数字中随机挑出3个不同的数字,记事件A1:恰好挑出的是1、2、3;记事件A2:恰好挑出的是1、4、7;记事件A3:挑出的数字里含有数字1.下列说法正确的是( )
1 2 3
4 5 6
7 8 9
A.事件A1,A2是互斥事件
B.事件A1,A2是独立事件
C.P(A1|A3)=P(A2|A3)
D.P(A3)=P(A1)+P(A2)
11.我国南宋数学家杨辉1261年所著的《详解九章算法》给出了著名的杨辉三角,在杨辉三角(左图)中,除1以外的每一个数都等于它“肩上”两个数的和,第n行所有数之和为;右图是英国生物学家高尔顿设计的模型高尔顿板,在一块木板上钉着若干排相互平行且相互错开的圆柱形钉子,钉子之间留有空隙作为通道,让一个小球从高尔顿板上方的入口落下,小球在下落的过程中与钉子碰撞,且等可能向左或向右滚下,最后掉到下方的某一球槽内,如图,小球从高尔顿板第1行的第一个缝隙落下的概率是,第二个缝隙落下的概率是;从第2行第一个缝隙落下的概率是,第二个缝腺落下的概率是,第三个缝隙落下的概率是,小球从第n行第m个缝隙落下的概率可以由杨辉三角快速算出,那么小球从第6行某个缝隙落下的概率可能为( )
A. B. C. D.
12.医用口罩由口罩面体和拉紧带组成,其中口罩面体分为内、中、外三层.内层为亲肤材质(普通卫生纱布或无纺布),中层为隔离过滤层(超细聚丙烯纤维熔喷材料层),外层为特殊材料抑菌层(无纺布或超薄聚丙烯熔喷材料层).根据国家质量监督检验标准,医用口罩的过滤率是重要的指标,根据长期生产经验,某企业在生产线状态正常情况下生产的医用口罩的过滤率,则下列说法正确的是(附:若,则,,)( )
A.
B.
C.
D.假设生产状态正常,记表示一天内抽取的50只医用口罩中过滤率大于等于的数量,则
填空题(本大题共4小题,每小题5分,共20分)
13.已知随机变量X的概率分布为,则实数______.
14.设盒中装有5只灯泡,其中3只是好的,2只是坏的,现从盒中随机地摸出两只,并换进2只好的之后,再从盒中摸出2只,则第二次摸出的2只全是好的概率为________.
15.甲乙两人进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时停止.设甲、乙在每局中获胜的概率均为,且各局胜负相互独立,比赛停止时一共打了局,则的方差______.
16.某校高二学生一次数学诊断考试成绩(单位:分)服从正态分布,从中抽取一个同学的数学成绩,记该同学的成绩为事件,记该同学的成绩为事件,则在事件发生的条件下事件发生的概率______.(结果用分数表示)
附参考数据:;;.
四、解答题(本大题共6小题,共70分)
17.共享电动车(sharedev)是一种新的交通工具,通过扫码开锁,实现循环共享.某记者来到中国传媒大学探访,在校园喷泉旁停放了10辆共享电动车,这些电动车分为荧光绿和橙色两种颜色,已知从这些共享电动车中任取1辆,取到的是橙色的概率为,若从这些共享电动车中任意抽取3辆.
(1)求取出的3辆共享电动车中恰好有一辆是橙色的概率;
(2)求取出的3辆共享电动车中橙色的电动车的辆数X的分布列与数学期望.
18.抛掷两枚质地均匀的骰子,一枚红色,一枚蓝色.事件:“两枚骰子的点数相同”,事件:“红骰子的点数小于蓝骰子的点数”,事件:“两枚骰子的点数之和是6".分别计算事件,,的概率.
19.“弘扬中华优秀传统文化经验交流大会”于年月日在深圳举行,会议同期举行了“深圳市中华优秀传统文化公益讲堂”启动仪式.从年月起到月,深圳市文化和健康发展促进会将连续举办场中华优秀传统文化公益讲堂,邀请多位名家名师现场开讲.某学校文学社为响应这次活动,举办了中华古诗词背诵比赛,统计的比赛成绩(单位:分)的数据如频率分布直方图所示,已知成绩在内的有人.
(1)求的值及参加比赛的总人数;
(2)分别从、分数段中选取人和人组成“优胜”队,与另一学校的“必胜”队的人进行友谊赛,两队的选手每人均比赛局,共比赛局,胜局得分,输局得分,没有平局.已知“优胜”队中成绩在内的选手获胜的概率为,在内的名选手获胜的概率分别为、,记“优胜”队的得分为随机变量,求的分布列和期望.
20.党的十九届五中全会强调“创新”在我国现代化建设中的重要战略地位,确保发展经济着力点放在实体经济上,为促进经济活力,拉动市场经济快速发展,必须大力推进大众创业、万众创新.某几位大学毕业生自主创业创办了一家服务公司,该公司提供、两种民生消费产品(人们购买时每次只买其中一种)服务,他们经过统计分析发现:第一次购买产品的人购买产品的概率为,购买产品的概率为,而前一次购买产品的人下一次来购买产品的概率为,购买产品的概率为,前一次购买产品的人下一次来购买产品的概率为,购买产品的概率也是,如此往复.记某人第次来购买产品的概率为.
(1)求;
(2)记第二次来公司购买产品的个人中有个人购买产品,人是否购买产品相互独立,求的分布列和数学期望.
21.年五一节期间,我国高速公路继续执行“节假日高速公路免费政策”.某路桥公司为掌握五一节期间车辆出行的高峰情况,在某高速公路收费站点记录了日上午这一时间段内通过的车辆数,统计发现这一时间段内共有辆车通过该收费站点,它们通过该收费站点的时刻的频率分布直方图如下图所示,其中时间段记作,记作,记作,记作,例如:,记作时刻.
(1)估计这辆车在时间内通过该收费站点的时刻的平均值(同一组中的数据用该组区间的中点值代替)
(2)为了对数据进行分析,现采用分层抽样的方法从这辆车中抽取辆,再从这辆车中随机抽取辆,设抽到的辆车中,在之间通过的车辆数为,求的分布列;
(3)根据大数据分析,车辆在每天通过该收费站点的时刻服从正态分布,其中可用日数据中的辆车在之间通过该收费站点的时刻的平均值近似代替,用样本的方差近似代替(经计算样本方差为).假如日上午这一时间段内共有辆车通过该收费站点,估计在之间通过的车辆数(结果保留到整数)
附:;若随机变量服从正态分布,则,,.
22.2020年8月,教育部发布《关于深化体教融合,促进青少年健康发展的意见》某校积极响应国家号召,组织全校学生加强实心球项目训练,规定该校男生投掷实心球米达标,女生投掷实心球米达标,并拟定投掷实心球的考试方案为每生可以投掷3次,一旦达标无需再投.从该校任选5名学生进行测试,如果有2人不达标的概率超过0.1,则该校学生还需加强实心球项目训练,已知该校男生投掷实心球的距离服从正态分布,女生投掷实心球的距离服从正态分布(的单位:米).
(1)请你通过计算,判断该校学生是否还需加强实心球项目训练;
(2)为提高学生考试达标率,该校决定加强训练,经过一段时间训练后,该校女生投掷实心球的距离服从正态分布,且.此时,请判断该校女生投掷实心球的考试达标率能否达到?并说明理由.(取的值为2.15)
第七章《随机变量及其分布》同步单元高分突破必刷卷(培优版)
全解全析
1.B
【解析】
【分析】
利用条件概率求解.
【详解】
设“第一次摸到红球”的事件为A,设“第二次摸到白球”的事件为B,
则 ,
所以在第一次摸到的是红球的条件下,第二次第二次摸到白球的概率为:
.
故选:B
2.B
【解析】
【分析】
根据题意得,进而根据题意计算期望与方程即可.
【详解】
解:由分布列的性质,得,
所以,
所以,
又,所以.
故选:B
3.B
【解析】
【分析】
根据正态分布的对称性得到对称轴为,得到摄像头在4年内能正常工作的概率为,再计算概率得到答案.
【详解】
,,所以.
所以正态分布曲线的对称轴为,即,
即一个摄像头在4年内能正常工作的概率为.
所以两个该品牌的摄像头在4年内都能正常工作的概率为.
故选:B.
4.B
【解析】
【分析】
利用正态分布的性质得出的值,进而估计所抽取的这批无人机配件中质量指标值低于的个数.
【详解】
因为服从正态分布,所以
则
且在区间内的个数为,故可估计值约万个.
则
故可估计所抽取的这批无人机配件中质量指标值低于的个数大约为.
故选:B.
5.C
【解析】
【分析】
根据给定条件可得随机变量X和Y所对的正态密度曲线的形状相同,进而得出,再求出即可计算作答.
【详解】
因随机变量X,Y满足X~N(3,),Y~N(1,),则随机变量X和Y所对的正态密度曲线的形状相同,它们的对称轴分别为和,
因此,,而Z=Y-1,则,
于是得,
所以P(Z2<1)的值为0.8.
故选:C
6.D
【解析】
【分析】
先求得的表达式,结合二次函数的性质,由的最大值列不等式,从而求得的取值范围.
【详解】
由的分布列,可得.又,所以
.
因为,所以当且仅当时,取得最大值,为.
又对所有成立,所以,解得,
又,所以.
故选:D
7.B
【解析】
【分析】
由于,利用随机变量的分布列列式,求出和,由此可求出,再由,即可求出结果.
【详解】
解:根据题意,可知:,则,
,即:,
解得:,,
,
则,
所以.
故选:B.
【点睛】
本题考查离散型随机变量的方差的求法,以及离散型随机变量的分布列、数学期望等知识,考查运算求解能力.
8.C
【解析】
【分析】
先求出每道题的得分期望值,再由40道选择题的期望得分,即可求学生在本次竞赛时得分的均值.
【详解】
由题设,每道题期望分值为,
∴40道选择题的期望得分为.
故选:C
9.BCD
【解析】
【分析】
利用条件逐项分析即得.
【详解】
对于A,第一次摸到红球的概率为,故A错误;
对于B,不放回的摸球2次,则在第一次摸到红球的条件下第二次摸到红球的概率为,故B正确;
对于C,有放回的摸球3次,仅有前2次摸到红球的概率为,故C正确;
对于D,有放回的摸球3次,则恰有2次摸到红球的概率为,故D正确.
故选:BCD.
10.AC
【解析】
【分析】
根据互斥事件和相互独立事件的概念判断AB;利用条件概率公式计算概率判断C;计算判断D.
【详解】
A.挑出的是1、2、3和挑出的是1、4、7不可能同时发生,正确;
B.事件A1,A2不是独立事件,错误;
C.,正确;
D. ,,错误.
故选:AC.
11.BC
【解析】
【分析】
利用n次独立重复试验中事件A恰好发生k次的概率公式,计算m取各个值的概率即可判断作答.
【详解】
小球落下要经过6次碰撞,每次向左、向右落下的概率均为,
小球从第6行第m个缝隙落下,则6次碰撞有次向右,
其概率为,,
于是得,,,,
所以选项A,D不可能,选项B,C可能.
故选:BC
12.ABC
【解析】
【分析】
利用正态曲线的对称性可以判定A,B,C,然后再求出一只口罩过滤率小于等于的概率,进而根据独立事件和对立事件的概率求出.
【详解】
由题意可知,,.对于A,因为,所以,故A正确;
对于B,因为,,所以根据正态密度曲线的特点可知,故B正确;
对于C,因为,且,所以,故C正确;
对于D,一只医用口罩过滤率小于的概率约为,所以,故D错误.
故选:ABC.
13.
【解析】
【分析】
根据给定条件利用随机变量分布列的性质列式计算作答.
【详解】
依题意,,
由分布列的性质得,解得,
所以实数.
故答案为:
14.0.55##
【解析】
【分析】
Ai(i=0,1,2)、A分别表示“第一次摸出i只好的”、 “第二次摸出的2只全是好的”,则有P(A)=P(AA2)+ P(AA1)+P(AA0),结合题设即可求第二次摸出的2只全是好的概率.
【详解】
Ai=“第一次摸出i只好的”(i=0,1,2),A=“第二次摸出的2只全是好的”,则P(A)=P(AA2)+ P(AA1)+P(AA0),
∵P(A0)=,P(A|A0)=1,P(A1)=,P(A|A1)=,P(A2)=,P(A|A2)=,
∴第二次摸出的2只全是好的的概率为P(A)=P(A2)·P(A|A2)+P(A1)P(A|A1)+P(A0)P(A|A0)=.
故答案为:
15.
【解析】
【分析】
首先将每两局比赛为一轮,计算出一轮比赛结束时比赛停止的概率,根据题意可能的取值为,,,分别计算出相应的概率,计算数学期望,利用方差公式即可求解.
【详解】
因为比赛进行到有一人比对方多2分或打满6局时停止,所以可能的取值为,,,
设每两局比赛为一轮,则该轮结束时比赛停止的概率,
,
,
,
所以,
所以,
故答案为:.
16.
【解析】
【分析】
计算出和,然后利用条件概率公式可得出的值.
【详解】
由题意可知,,事件为,,,
所以,,
,
由条件概率公式得,故答案为.
【点睛】
本题考查条件概率的计算,同时也考查了正态分布原则计算概率,解题时要将相应的事件转化为正态分布事件,充分利用正态密度曲线的对称性计算,考查计算能力,属于中等题.
17.(1);
(2)分布列见解析,数学期望为.
【解析】
【分析】
(1)先求出两种颜色的电动车各有多少辆,然后根据超几何分布求概率的方法即可求得答案;
(2)先确定X的所有可能取值,进而求出概率并列出分布列,然后根据期望公式求出答案.
(1)
因为从10辆共享电动车中任取一辆,取到橙色的概率为0.4,所以橙色的电动车有4辆,荧光绿的电动车有6辆.
记A为“从中任取3辆共享单车中恰好有一辆是橙色”,则.
(2)
随机变量X的所有可能取值为0,1,2,3.
所以,,
,.
所以分布列为
0 1 2 3
数学期望.
18.,,
【解析】
【分析】
依据古典概型和条件概率的计算公式去求解即可得到事件,,的概率.
【详解】
抛掷两枚质地均匀的骰子,一枚红色,一枚蓝色.可以得到36个基本事件
(红1,蓝1),(红1,蓝2),(红1,蓝3),(红1,蓝4),(红1,5),(红1,蓝6)
(红2,蓝1),(红2,蓝2),(红2,蓝3),(红2,蓝4),(红2,5),(红2,蓝6)
(红3,蓝1),(红3,蓝2),(红3,蓝3),(红3,蓝4),(红3,5),(红3,蓝6)
(红4,蓝1),(红4,蓝2),(红4,蓝3),(红4,蓝4),(红4,5),(红4,蓝6)
(红5,蓝1),(红5,蓝2),(红5,蓝3),(红5,蓝4),(红5,5),(红5,蓝6)
(红6,蓝1),(红6,蓝2),(红6,蓝3),(红6,蓝4),(红6,5),(红6,蓝6)
事件包含21个基本事件,
事件包含10个基本事件,
事件包含2个基本事件,
事件包含15个基本事件,
则
19.(1),参加比赛的总人数为;
(2)分布列见解析,.
【解析】
【分析】
(1)利用频率分布直方图中所有矩形的面积之和为可求得的值,将成绩在内的人数除以该组的频率可得出参加比赛的总人数;
(2)分析可知,随机变量的所有可能取值有、、、,计算出随机变量在不同取值下的概率,可得出随机变量的分布列,进一步可求得的值.
(1)
解:由频率分布直方图可得,解得,
参加比赛的总人数为.
(2)
解:的所有可能取值有、、、,,
,
,,
所以,随机变量的分布列如下表所示:
因此,.
20.(1)
(2)分布列见解析,数学期望为1
【解析】
【分析】
(1)根据概率公式求出;
(2)根据二项分布的概率公式求得的各种取值所对应的概率,再计算出期望即可.
(1)
某人第次来购买产品的概率为,即;
(2)
由题意得,其中的可能取值有,,,,
故,,,;
故的分布列为
的数学期望为
.
21.(1)64
(2)答案见解析
(3)819
【解析】
【分析】
(1)由频率分布直方图即能求出这600辆车在时间段内通过该收费点的时刻的平均值.
(2)由频率分布直方图和分层抽样的方法可知,抽取的10辆车中,在前通过的车辆数就是位于时间分组,这一区间内的车辆数,求出其结果为4,从而的可能的取值为0,1,2,3,4,分别求出相应的概率,由此能求出的分布列.
(3)求出,,估计在之间通过的车辆数也就是在,通过的车辆数,由,,即能估计在之间通过的车辆数.
(1)
这600辆车在时间段内通过该收费点的时刻的平均值为:
.
(2)
由频率分布直方图和分层抽样的方法可知,抽取的10辆车中,
在前通过的车辆数就是位于时间分组,这一区间内的车辆数,
即,
所以的可能的取值为0,1,2,3,4.
所以,,,,.
所以的分布列为:
0 1 2 3 4
(3)
由(1)得,
由已知,所以,
估计在之间通过的车辆数也就是在,通过的车辆数,
由,得:
,
所以估计在在之间通过的车辆数为.
22.(1)需要加强
(2)该校女生投掷实心球的考试达标率能达到,理由见解析
【解析】
【分析】
(1)根据独立重复试验概率计算公式进行计算,从而作出判断.
(2)通过计算达标率来进行说明.
(1)
依题意该校男生投掷实心球的距离服从正态分布,女生投掷实心球的距离服从正态分布,
所以男生和女生的达标概率为,不达标概率为,
所以从该校任选5名学生进行测试,如果有2人不达标的概率为,
所以该校学生还需加强实心球项目训练.
(2)
,即,
且,即,
所以,
,
则女生达标率为.
所以该校女生投掷实心球的考试达标率能达到.
(时间:120分钟 满分:150分)
单项选择题(本大题共8小题,每小题5分,共40分)
1.袋子中装有大小、形状完全相同的2个白球和2个红球,现从中不放回地摸取两个球,已知第一次摸到的是红球,则第二次摸到白球的概率为( )
A. B. C. D.
2.已知随机变量满足,且随机变量的分布列如下:
0 1 2
则随机变量的方差( )A. B. C. D.
3.某种品牌摄像头的使用寿命(单位:年)服从正态分布,且使用寿命不少于2年的概率为0.8,使用寿命不少于6年的概率为0.2.某校在大门口同时安装了两个该种品牌的摄像头,则在4年内这两个摄像头都能正常工作的概率为( )
A.0.2 B.0.25
C.0.4 D.0.8
4.某无人机配件厂商从其所生产的某种无人机配件中随机抽取了一部分进行质量检测,其某项质量测试指标值X服从正态分布,且落在区间内的无人机配件个数为则可估计所抽取的这批无人机配件中质量指标值低于的个数大约为( )
(附:若随机变量服从正态分布,则
A. B. C. D.
5.已知随机变量X,Y,Z满足X~N(3,),Y~N(1,),Z=Y-1,且P(X>4)=0.1,则P(Z2<1)的值为( )
A.0.1 B.0.2
C.0.8 D.0.9
6.已知随机变量的分布列如表所示:
0 1
其中.若对所有都成立,则的取值范围为( )
A. B. C. D.
7.随机变量的分布列如下表所示,若,则
-1 0 1
A.4 B.5 C.6 D.7
8.为喜迎“中国共产党建党100华诞”,某中学高二年级历史方向类的班级举行“党史知识”竞赛.在本次竞赛中共有40道选择题,每道选择题都有4个选项,其中有且只有一个选项是正确的.评分标准规定:“每题只选一个选项,答对得5分,不答或答错倒扣2分”.某学生每道题答对的概率都为,则该学生在本次竞赛时得分的均值为( )
A.36 B.32 C.172 D.144
多项选择题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得3分,有选错的得0分)
9.一个袋子中装有除颜色外完全相同的5个球.,其中有3个红球,2个白球,每次从中随机摸出1个球,则下列结论中正确的是( )
A.若不放回的摸球2次,则第一次摸到红球的概率为
B.若不放回的摸球2次,则在第一次摸到红球的条件下第二次摸到红球的概率为
C.若有放回的摸球3次,仅有前2次摸到红球的概率为
D.若有放回的摸球3次,则恰有2次摸到红球的概率为
10.如图所示,是一个3×3九宫格,现从这9个数字中随机挑出3个不同的数字,记事件A1:恰好挑出的是1、2、3;记事件A2:恰好挑出的是1、4、7;记事件A3:挑出的数字里含有数字1.下列说法正确的是( )
1 2 3
4 5 6
7 8 9
A.事件A1,A2是互斥事件
B.事件A1,A2是独立事件
C.P(A1|A3)=P(A2|A3)
D.P(A3)=P(A1)+P(A2)
11.我国南宋数学家杨辉1261年所著的《详解九章算法》给出了著名的杨辉三角,在杨辉三角(左图)中,除1以外的每一个数都等于它“肩上”两个数的和,第n行所有数之和为;右图是英国生物学家高尔顿设计的模型高尔顿板,在一块木板上钉着若干排相互平行且相互错开的圆柱形钉子,钉子之间留有空隙作为通道,让一个小球从高尔顿板上方的入口落下,小球在下落的过程中与钉子碰撞,且等可能向左或向右滚下,最后掉到下方的某一球槽内,如图,小球从高尔顿板第1行的第一个缝隙落下的概率是,第二个缝隙落下的概率是;从第2行第一个缝隙落下的概率是,第二个缝腺落下的概率是,第三个缝隙落下的概率是,小球从第n行第m个缝隙落下的概率可以由杨辉三角快速算出,那么小球从第6行某个缝隙落下的概率可能为( )
A. B. C. D.
12.医用口罩由口罩面体和拉紧带组成,其中口罩面体分为内、中、外三层.内层为亲肤材质(普通卫生纱布或无纺布),中层为隔离过滤层(超细聚丙烯纤维熔喷材料层),外层为特殊材料抑菌层(无纺布或超薄聚丙烯熔喷材料层).根据国家质量监督检验标准,医用口罩的过滤率是重要的指标,根据长期生产经验,某企业在生产线状态正常情况下生产的医用口罩的过滤率,则下列说法正确的是(附:若,则,,)( )
A.
B.
C.
D.假设生产状态正常,记表示一天内抽取的50只医用口罩中过滤率大于等于的数量,则
填空题(本大题共4小题,每小题5分,共20分)
13.已知随机变量X的概率分布为,则实数______.
14.设盒中装有5只灯泡,其中3只是好的,2只是坏的,现从盒中随机地摸出两只,并换进2只好的之后,再从盒中摸出2只,则第二次摸出的2只全是好的概率为________.
15.甲乙两人进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时停止.设甲、乙在每局中获胜的概率均为,且各局胜负相互独立,比赛停止时一共打了局,则的方差______.
16.某校高二学生一次数学诊断考试成绩(单位:分)服从正态分布,从中抽取一个同学的数学成绩,记该同学的成绩为事件,记该同学的成绩为事件,则在事件发生的条件下事件发生的概率______.(结果用分数表示)
附参考数据:;;.
四、解答题(本大题共6小题,共70分)
17.共享电动车(sharedev)是一种新的交通工具,通过扫码开锁,实现循环共享.某记者来到中国传媒大学探访,在校园喷泉旁停放了10辆共享电动车,这些电动车分为荧光绿和橙色两种颜色,已知从这些共享电动车中任取1辆,取到的是橙色的概率为,若从这些共享电动车中任意抽取3辆.
(1)求取出的3辆共享电动车中恰好有一辆是橙色的概率;
(2)求取出的3辆共享电动车中橙色的电动车的辆数X的分布列与数学期望.
18.抛掷两枚质地均匀的骰子,一枚红色,一枚蓝色.事件:“两枚骰子的点数相同”,事件:“红骰子的点数小于蓝骰子的点数”,事件:“两枚骰子的点数之和是6".分别计算事件,,的概率.
19.“弘扬中华优秀传统文化经验交流大会”于年月日在深圳举行,会议同期举行了“深圳市中华优秀传统文化公益讲堂”启动仪式.从年月起到月,深圳市文化和健康发展促进会将连续举办场中华优秀传统文化公益讲堂,邀请多位名家名师现场开讲.某学校文学社为响应这次活动,举办了中华古诗词背诵比赛,统计的比赛成绩(单位:分)的数据如频率分布直方图所示,已知成绩在内的有人.
(1)求的值及参加比赛的总人数;
(2)分别从、分数段中选取人和人组成“优胜”队,与另一学校的“必胜”队的人进行友谊赛,两队的选手每人均比赛局,共比赛局,胜局得分,输局得分,没有平局.已知“优胜”队中成绩在内的选手获胜的概率为,在内的名选手获胜的概率分别为、,记“优胜”队的得分为随机变量,求的分布列和期望.
20.党的十九届五中全会强调“创新”在我国现代化建设中的重要战略地位,确保发展经济着力点放在实体经济上,为促进经济活力,拉动市场经济快速发展,必须大力推进大众创业、万众创新.某几位大学毕业生自主创业创办了一家服务公司,该公司提供、两种民生消费产品(人们购买时每次只买其中一种)服务,他们经过统计分析发现:第一次购买产品的人购买产品的概率为,购买产品的概率为,而前一次购买产品的人下一次来购买产品的概率为,购买产品的概率为,前一次购买产品的人下一次来购买产品的概率为,购买产品的概率也是,如此往复.记某人第次来购买产品的概率为.
(1)求;
(2)记第二次来公司购买产品的个人中有个人购买产品,人是否购买产品相互独立,求的分布列和数学期望.
21.年五一节期间,我国高速公路继续执行“节假日高速公路免费政策”.某路桥公司为掌握五一节期间车辆出行的高峰情况,在某高速公路收费站点记录了日上午这一时间段内通过的车辆数,统计发现这一时间段内共有辆车通过该收费站点,它们通过该收费站点的时刻的频率分布直方图如下图所示,其中时间段记作,记作,记作,记作,例如:,记作时刻.
(1)估计这辆车在时间内通过该收费站点的时刻的平均值(同一组中的数据用该组区间的中点值代替)
(2)为了对数据进行分析,现采用分层抽样的方法从这辆车中抽取辆,再从这辆车中随机抽取辆,设抽到的辆车中,在之间通过的车辆数为,求的分布列;
(3)根据大数据分析,车辆在每天通过该收费站点的时刻服从正态分布,其中可用日数据中的辆车在之间通过该收费站点的时刻的平均值近似代替,用样本的方差近似代替(经计算样本方差为).假如日上午这一时间段内共有辆车通过该收费站点,估计在之间通过的车辆数(结果保留到整数)
附:;若随机变量服从正态分布,则,,.
22.2020年8月,教育部发布《关于深化体教融合,促进青少年健康发展的意见》某校积极响应国家号召,组织全校学生加强实心球项目训练,规定该校男生投掷实心球米达标,女生投掷实心球米达标,并拟定投掷实心球的考试方案为每生可以投掷3次,一旦达标无需再投.从该校任选5名学生进行测试,如果有2人不达标的概率超过0.1,则该校学生还需加强实心球项目训练,已知该校男生投掷实心球的距离服从正态分布,女生投掷实心球的距离服从正态分布(的单位:米).
(1)请你通过计算,判断该校学生是否还需加强实心球项目训练;
(2)为提高学生考试达标率,该校决定加强训练,经过一段时间训练后,该校女生投掷实心球的距离服从正态分布,且.此时,请判断该校女生投掷实心球的考试达标率能否达到?并说明理由.(取的值为2.15)
第七章《随机变量及其分布》同步单元高分突破必刷卷(培优版)
全解全析
1.B
【解析】
【分析】
利用条件概率求解.
【详解】
设“第一次摸到红球”的事件为A,设“第二次摸到白球”的事件为B,
则 ,
所以在第一次摸到的是红球的条件下,第二次第二次摸到白球的概率为:
.
故选:B
2.B
【解析】
【分析】
根据题意得,进而根据题意计算期望与方程即可.
【详解】
解:由分布列的性质,得,
所以,
所以,
又,所以.
故选:B
3.B
【解析】
【分析】
根据正态分布的对称性得到对称轴为,得到摄像头在4年内能正常工作的概率为,再计算概率得到答案.
【详解】
,,所以.
所以正态分布曲线的对称轴为,即,
即一个摄像头在4年内能正常工作的概率为.
所以两个该品牌的摄像头在4年内都能正常工作的概率为.
故选:B.
4.B
【解析】
【分析】
利用正态分布的性质得出的值,进而估计所抽取的这批无人机配件中质量指标值低于的个数.
【详解】
因为服从正态分布,所以
则
且在区间内的个数为,故可估计值约万个.
则
故可估计所抽取的这批无人机配件中质量指标值低于的个数大约为.
故选:B.
5.C
【解析】
【分析】
根据给定条件可得随机变量X和Y所对的正态密度曲线的形状相同,进而得出,再求出即可计算作答.
【详解】
因随机变量X,Y满足X~N(3,),Y~N(1,),则随机变量X和Y所对的正态密度曲线的形状相同,它们的对称轴分别为和,
因此,,而Z=Y-1,则,
于是得,
所以P(Z2<1)的值为0.8.
故选:C
6.D
【解析】
【分析】
先求得的表达式,结合二次函数的性质,由的最大值列不等式,从而求得的取值范围.
【详解】
由的分布列,可得.又,所以
.
因为,所以当且仅当时,取得最大值,为.
又对所有成立,所以,解得,
又,所以.
故选:D
7.B
【解析】
【分析】
由于,利用随机变量的分布列列式,求出和,由此可求出,再由,即可求出结果.
【详解】
解:根据题意,可知:,则,
,即:,
解得:,,
,
则,
所以.
故选:B.
【点睛】
本题考查离散型随机变量的方差的求法,以及离散型随机变量的分布列、数学期望等知识,考查运算求解能力.
8.C
【解析】
【分析】
先求出每道题的得分期望值,再由40道选择题的期望得分,即可求学生在本次竞赛时得分的均值.
【详解】
由题设,每道题期望分值为,
∴40道选择题的期望得分为.
故选:C
9.BCD
【解析】
【分析】
利用条件逐项分析即得.
【详解】
对于A,第一次摸到红球的概率为,故A错误;
对于B,不放回的摸球2次,则在第一次摸到红球的条件下第二次摸到红球的概率为,故B正确;
对于C,有放回的摸球3次,仅有前2次摸到红球的概率为,故C正确;
对于D,有放回的摸球3次,则恰有2次摸到红球的概率为,故D正确.
故选:BCD.
10.AC
【解析】
【分析】
根据互斥事件和相互独立事件的概念判断AB;利用条件概率公式计算概率判断C;计算判断D.
【详解】
A.挑出的是1、2、3和挑出的是1、4、7不可能同时发生,正确;
B.事件A1,A2不是独立事件,错误;
C.,正确;
D. ,,错误.
故选:AC.
11.BC
【解析】
【分析】
利用n次独立重复试验中事件A恰好发生k次的概率公式,计算m取各个值的概率即可判断作答.
【详解】
小球落下要经过6次碰撞,每次向左、向右落下的概率均为,
小球从第6行第m个缝隙落下,则6次碰撞有次向右,
其概率为,,
于是得,,,,
所以选项A,D不可能,选项B,C可能.
故选:BC
12.ABC
【解析】
【分析】
利用正态曲线的对称性可以判定A,B,C,然后再求出一只口罩过滤率小于等于的概率,进而根据独立事件和对立事件的概率求出.
【详解】
由题意可知,,.对于A,因为,所以,故A正确;
对于B,因为,,所以根据正态密度曲线的特点可知,故B正确;
对于C,因为,且,所以,故C正确;
对于D,一只医用口罩过滤率小于的概率约为,所以,故D错误.
故选:ABC.
13.
【解析】
【分析】
根据给定条件利用随机变量分布列的性质列式计算作答.
【详解】
依题意,,
由分布列的性质得,解得,
所以实数.
故答案为:
14.0.55##
【解析】
【分析】
Ai(i=0,1,2)、A分别表示“第一次摸出i只好的”、 “第二次摸出的2只全是好的”,则有P(A)=P(AA2)+ P(AA1)+P(AA0),结合题设即可求第二次摸出的2只全是好的概率.
【详解】
Ai=“第一次摸出i只好的”(i=0,1,2),A=“第二次摸出的2只全是好的”,则P(A)=P(AA2)+ P(AA1)+P(AA0),
∵P(A0)=,P(A|A0)=1,P(A1)=,P(A|A1)=,P(A2)=,P(A|A2)=,
∴第二次摸出的2只全是好的的概率为P(A)=P(A2)·P(A|A2)+P(A1)P(A|A1)+P(A0)P(A|A0)=.
故答案为:
15.
【解析】
【分析】
首先将每两局比赛为一轮,计算出一轮比赛结束时比赛停止的概率,根据题意可能的取值为,,,分别计算出相应的概率,计算数学期望,利用方差公式即可求解.
【详解】
因为比赛进行到有一人比对方多2分或打满6局时停止,所以可能的取值为,,,
设每两局比赛为一轮,则该轮结束时比赛停止的概率,
,
,
,
所以,
所以,
故答案为:.
16.
【解析】
【分析】
计算出和,然后利用条件概率公式可得出的值.
【详解】
由题意可知,,事件为,,,
所以,,
,
由条件概率公式得,故答案为.
【点睛】
本题考查条件概率的计算,同时也考查了正态分布原则计算概率,解题时要将相应的事件转化为正态分布事件,充分利用正态密度曲线的对称性计算,考查计算能力,属于中等题.
17.(1);
(2)分布列见解析,数学期望为.
【解析】
【分析】
(1)先求出两种颜色的电动车各有多少辆,然后根据超几何分布求概率的方法即可求得答案;
(2)先确定X的所有可能取值,进而求出概率并列出分布列,然后根据期望公式求出答案.
(1)
因为从10辆共享电动车中任取一辆,取到橙色的概率为0.4,所以橙色的电动车有4辆,荧光绿的电动车有6辆.
记A为“从中任取3辆共享单车中恰好有一辆是橙色”,则.
(2)
随机变量X的所有可能取值为0,1,2,3.
所以,,
,.
所以分布列为
0 1 2 3
数学期望.
18.,,
【解析】
【分析】
依据古典概型和条件概率的计算公式去求解即可得到事件,,的概率.
【详解】
抛掷两枚质地均匀的骰子,一枚红色,一枚蓝色.可以得到36个基本事件
(红1,蓝1),(红1,蓝2),(红1,蓝3),(红1,蓝4),(红1,5),(红1,蓝6)
(红2,蓝1),(红2,蓝2),(红2,蓝3),(红2,蓝4),(红2,5),(红2,蓝6)
(红3,蓝1),(红3,蓝2),(红3,蓝3),(红3,蓝4),(红3,5),(红3,蓝6)
(红4,蓝1),(红4,蓝2),(红4,蓝3),(红4,蓝4),(红4,5),(红4,蓝6)
(红5,蓝1),(红5,蓝2),(红5,蓝3),(红5,蓝4),(红5,5),(红5,蓝6)
(红6,蓝1),(红6,蓝2),(红6,蓝3),(红6,蓝4),(红6,5),(红6,蓝6)
事件包含21个基本事件,
事件包含10个基本事件,
事件包含2个基本事件,
事件包含15个基本事件,
则
19.(1),参加比赛的总人数为;
(2)分布列见解析,.
【解析】
【分析】
(1)利用频率分布直方图中所有矩形的面积之和为可求得的值,将成绩在内的人数除以该组的频率可得出参加比赛的总人数;
(2)分析可知,随机变量的所有可能取值有、、、,计算出随机变量在不同取值下的概率,可得出随机变量的分布列,进一步可求得的值.
(1)
解:由频率分布直方图可得,解得,
参加比赛的总人数为.
(2)
解:的所有可能取值有、、、,,
,
,,
所以,随机变量的分布列如下表所示:
因此,.
20.(1)
(2)分布列见解析,数学期望为1
【解析】
【分析】
(1)根据概率公式求出;
(2)根据二项分布的概率公式求得的各种取值所对应的概率,再计算出期望即可.
(1)
某人第次来购买产品的概率为,即;
(2)
由题意得,其中的可能取值有,,,,
故,,,;
故的分布列为
的数学期望为
.
21.(1)64
(2)答案见解析
(3)819
【解析】
【分析】
(1)由频率分布直方图即能求出这600辆车在时间段内通过该收费点的时刻的平均值.
(2)由频率分布直方图和分层抽样的方法可知,抽取的10辆车中,在前通过的车辆数就是位于时间分组,这一区间内的车辆数,求出其结果为4,从而的可能的取值为0,1,2,3,4,分别求出相应的概率,由此能求出的分布列.
(3)求出,,估计在之间通过的车辆数也就是在,通过的车辆数,由,,即能估计在之间通过的车辆数.
(1)
这600辆车在时间段内通过该收费点的时刻的平均值为:
.
(2)
由频率分布直方图和分层抽样的方法可知,抽取的10辆车中,
在前通过的车辆数就是位于时间分组,这一区间内的车辆数,
即,
所以的可能的取值为0,1,2,3,4.
所以,,,,.
所以的分布列为:
0 1 2 3 4
(3)
由(1)得,
由已知,所以,
估计在之间通过的车辆数也就是在,通过的车辆数,
由,得:
,
所以估计在在之间通过的车辆数为.
22.(1)需要加强
(2)该校女生投掷实心球的考试达标率能达到,理由见解析
【解析】
【分析】
(1)根据独立重复试验概率计算公式进行计算,从而作出判断.
(2)通过计算达标率来进行说明.
(1)
依题意该校男生投掷实心球的距离服从正态分布,女生投掷实心球的距离服从正态分布,
所以男生和女生的达标概率为,不达标概率为,
所以从该校任选5名学生进行测试,如果有2人不达标的概率为,
所以该校学生还需加强实心球项目训练.
(2)
,即,
且,即,
所以,
,
则女生达标率为.
所以该校女生投掷实心球的考试达标率能达到.
