【人教版九上数学优质课件】21.2.3 一元二次方程的解法(四)因式分解法 课件(共30张PPT)
文档属性
| 名称 | 【人教版九上数学优质课件】21.2.3 一元二次方程的解法(四)因式分解法 课件(共30张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 22:16:28 | ||
图片预览











文档简介
(共30张PPT)
九上数学同步优质课件
人教版九年级上册
一元二次方程的解法(四) --因式分解法
1.理解用因式分解法解方程的依据.
2.会用因式分解法解一些特殊的一元二次方程.(重点)
3.会根据方程的特点选用恰当的方法解一元二次方程.(难点)
1.把一个多项式化成几个整式积的形式,这种变形叫做把这个多项
式__________.
2.因式分解常用的方法有_________________________.
3.将下列各式分解因式:
(1) 7x2-21x (2) 2(a-3)2-a+3 (3) (y+3)2-(2y-3)2
因式分解
提公因式法、
公式法
解:
(1)原式=7x(x-3)
(2)原式=2(a-3)2-(a-3)=(a-3)[2(a-3)-1]=(a-3)(2a-7)
(3)原式=[(y+3)+(2y-3)][(y+3)-(2y-3)]=(y+3+2y-3)(y+3-2y+3)=3y(6-y)
一个数的平方与这个数的3倍有可能相等吗?如果相等,这个数是几?你是怎样求出来的?
小颖、小亮、小明都设这个数为x,根据题意,可得方程x2=3x. 但他们的解法各不相同. 他们做得对吗?
一个数的平方与这个数的3倍有可能相等吗?
小颖
小亮
小明
思考:三种方法都正确吗?谁的方法更简单?
知识精讲
如果a b=0,那么a=0,或b=0.
我们知道ab=0,那么a=0或b=0,类似的解方程(x+1)(x-1)=0时,可转化为两个一元一次方程x+1=0或x-1=0来解,你能求 (x-3)(x+5)=0的解吗?
(x-3)(x+5)=0
解:x-3=0或x+5=0
所以x1=3,x2=-5.
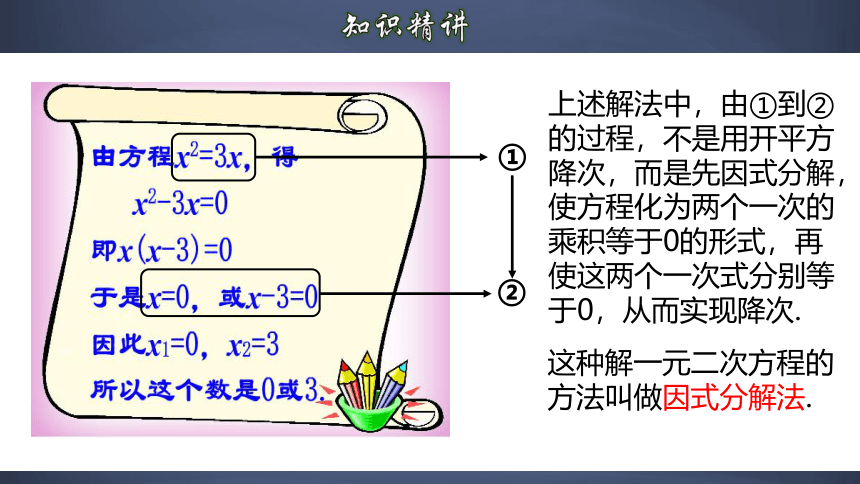
①
②
上述解法中,由①到②的过程,不是用开平方降次,而是先因式分解,使方程化为两个一次的乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次.
这种解一元二次方程的方法叫做因式分解法.
例1.解下列方程:
解:因式分解,得
于是得
x-2=0或x+1=0,
x1=2,x2=-1.
解:移项、合并同类项,得
因式分解,得
(2x+1)(2x-1)=0.
于是得
2x+1=0或2x-1=0,
(x-2)(x+1)=0.
可以试用多种方法解本例中的两个方程.
例1.解下列方程:
解:方程化为 x2-x-2=0
a=1,b=-1,c=-2
即 x1=2,x2=-1.
解:移项、合并同类项,得
系数化为1,得
直接开平方,得
Δ=b2-4ac
=(-1)2-4×1×(-2)=9>0
即
公式法
直接开平方法
配方法要先配方,再降次;通过配方法可以推出求根公式,公式法直接利用求根公式解方程;因式分解法要先使方程一边为两个一次因式相乘,另一边为0,再分别使各一次因式等于0. 配方法、公式法适用于所有一元二次方程,因式分解法在解某些一元二次方程时比较简便.
※解一元二次方程的基本思路是:将二次方程化为一次方程,即降次.
用因式分解法解下列方程:
解:x(x+1)=0
x=0或x+1=0
x1=0,x2=-1
解:
x=0或 x1=0,x2=
解:3x2-6x+3=0
x2-2x+1=0
(x-1)2=0
x1=x2=1
用因式分解法解下列方程:
解:(2x+11)(2x-11)=0 2x+11=0或2x-11=0
x1=-,x2=
解:3x(2x+1)-2(2x+1)=0 (2x+1)(3x-2)=0
2x+1=0或3x-2=0
x1=-,x2=
解:(x-4)2-(5-2x)2=0
(x-4+5-2x)(x-4-5+2x)=0
(1-x)(3x-9)=0
1-x=0或3x-9=0
x1=1,x2=3
例2.用适当的方法解方程:
【分析】方程一边以平方形式出现,另一边是常数,可直接开平方法.
【分析】二次项的系数为1,一次项的系数为偶数,可用配方法来解题较快.
解:x-1=±3
x-1=3或x-1=-3
∴x1=4,x2=-2
解:x2+2x+12=4+12
(x+1)2=5
∴x1= -1,x2= -1
x+1=±
例2.用适当的方法解方程:
【分析】方程左边变形后可以提取公因式,所以用因式分解法解答较快.
【分析】二次项的系数不为1,且不能直接开平方,也不能直接因式分解,所以适合公式法.
解:(x-2)2+2(x-2)=0
x=0或x-2=0
∴x1=0,x2=2
(x-2)(x-2+2)=0
x(x-2)=0
解:a=1,b=3,c=-4
即 x1=1,x2=-4.
Δ=b2-4ac=9+16=25>0
1.一般地,当一元二次方程一次项系数为0时(ax2+c=0),应选用直接开平方法;
2.若常数项为0(ax2+bx=0),应选用因式分解法;
3.若一次项系数和常数项都不为0 (ax2+bx+c=0),先化为一般式,看一边的整式是否容易因式分解,若容易,宜选用因式分解法,不然选用公式法;
4.不过当二次项系数是1,且一次项系数是偶数时,用配方法也较简单.
解法选择基本思路
用适当的方法解方程:
解:
3x-1=±2
∴x1=1,x2=-
解:x2+2x=48
(x+1)2=49
∴x1= -8,x2=
x+1=±
x2+2x+12=48+12
用适当的方法解方程:
解:a=2,b=-7,c=5
即 t1=,t2=1.
Δ=b2-4ac
=(-7)2-4×2×5=9>0
解:3(x-2)2=x2-4
∴x1=2,x2=4
(x-2)(3x-6-x-2)=0
3(x-2)2=(x+2)(x-2)
3(x-2)2-(x+2)(x-2)=0
(x-2)(2x-8)=0
1.一元二次方程(x-3)(x-5)=0的两根分别为( )
A.3,-5 B.3,5 C.-3,5 D.-3,-5
2.小华在解一元二次方程x2-x=0时,只得出一个根x=1,则被漏掉的一个根是( )
A.x=0 B.x=2 C.x=3 D.x=4
3.方程(x+1)(x-2)=x+1的解是( )
A.2 B.3 C.-1,2 D.-1,3
B
A
D
4.若分式 的值为零,则x的值是( )
A.3 B.-4 C.1或3 D.-1
A
5.一元二次方程x(x-5)=5-x的根是_______.
6.当x为_______时,代数式3x2的值与4x的值相等.
7.若(5x-6y)(x+y)=0, 则=______.
5和-1
0和
-1和
8.写出一个以-2和4为根的一元二次方程______________.
9.已知关于x的方程(x+a)(x-3)=0和x2-kx-3=0的根相同,则k=____,a=_____.
(x+2)(x-4)=0
2
1
【分析】由(x+a)(x-3)=0易得方程的一个根为x=3,
把x=3代入x2-kx-3=0得32-3k-3=0,
∴k=2得到方程x2-2x-3=0,
解得x1=-1,x2=3
∴-1+a=0,
∴a=1
① x2-3x+1=0; ②3x2-1=0; ③-3t2+t=0; ④x2-4x=2; ⑤2x2-x=0; ⑥5(m+2)2=8; ⑦3y2-y-1=0; ⑧2x2+4x-1=0; ⑨ (x-2)2=2(x-2).
适合运用直接开平方法 ;
适合运用因式分解法 ;
适合运用公式法 ;
适合运用配方法 .
⑥
①
②
③
④
⑤
⑦
⑧
⑨
10.填空:
达标检测
11.用适当的方法解方程:
解:(3x-2)2=(2x-1)2
∴x1=,x2=1
(3x-2+2x-1)(3x-2-2x+1)=0
(5x-3)(x-1)=0
(3x-2)2-(2x-1)2=0
解:
12.阅读材料:为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1视为一个整体,然后可设x2-1=y,则(x2-1)2=y2,原方程化为y2-5y+4=0①解得y1=1,y2=4.
当y=1时,x2-1=1.∴x2=2,∴x=±
当y=4时,x2-1=4.∴x2=5,∴x=±
∴原方程的解为x1=x2=-,x3=, x4=-
解答问题: (1)填空: 在由原方程得到方程①的过程中,利用_____法达到了降次的目的,体现了______的数学思想.
换元
转化
12.阅读材料:为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1视为一个整体,然后可设x2-1=y,则(x2-1)2=y2,原方程化为y2-5y+4=0①解得y1=1,y2=4.
当y=1时,x2-1=1.∴x2=2,∴x=±
当y=4时,x2-1=4.∴x2=5,∴x=±
∴原方程的解为x1=x2=-,x3=, x4=-
(2)解方程x4-5x2+6=0
解:设x2=y,则x4=y2
原方程化为y2-5y+6=0,解得y1=2,y2=3.
当y=2时,x2=2.∴x=±
当y=3时,x2=3.∴x=±
原方程的解为x1=x2=-,x3=, x4=-
一、概念:
二、原理:
三、基本步骤:
通过因式分解,将一个一元二次方程转化为两个一元一次方程来求解的方法叫做因式分解法.
如果a·b=0,那么a=0或b=0.
一移-----方程的右边=0;
二分-----方程的左边因式分解;
三化-----方程化为两个一元一次方程;
四解-----写出方程两个解;
简记歌诀:
右化零 左分解
两因式 各求解
1.一般地,当一元二次方程一次项系数为0时(ax2+c=0),应选用直接开平方法;
2.若常数项为0(ax2+bx=0),应选用因式分解法;
3.若一次项系数和常数项都不为0 (ax2+bx+c=0),先化为一般式,看一边的整式是否容易因式分解,若容易,宜选用因式分解法,不然选用公式法;
4.不过当二次项系数是1,且一次项系数是偶数时,用配方法也较简单.
解法选择基本思路
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步优质课件
人教版九年级上册
一元二次方程的解法(四) --因式分解法
1.理解用因式分解法解方程的依据.
2.会用因式分解法解一些特殊的一元二次方程.(重点)
3.会根据方程的特点选用恰当的方法解一元二次方程.(难点)
1.把一个多项式化成几个整式积的形式,这种变形叫做把这个多项
式__________.
2.因式分解常用的方法有_________________________.
3.将下列各式分解因式:
(1) 7x2-21x (2) 2(a-3)2-a+3 (3) (y+3)2-(2y-3)2
因式分解
提公因式法、
公式法
解:
(1)原式=7x(x-3)
(2)原式=2(a-3)2-(a-3)=(a-3)[2(a-3)-1]=(a-3)(2a-7)
(3)原式=[(y+3)+(2y-3)][(y+3)-(2y-3)]=(y+3+2y-3)(y+3-2y+3)=3y(6-y)
一个数的平方与这个数的3倍有可能相等吗?如果相等,这个数是几?你是怎样求出来的?
小颖、小亮、小明都设这个数为x,根据题意,可得方程x2=3x. 但他们的解法各不相同. 他们做得对吗?
一个数的平方与这个数的3倍有可能相等吗?
小颖
小亮
小明
思考:三种方法都正确吗?谁的方法更简单?
知识精讲
如果a b=0,那么a=0,或b=0.
我们知道ab=0,那么a=0或b=0,类似的解方程(x+1)(x-1)=0时,可转化为两个一元一次方程x+1=0或x-1=0来解,你能求 (x-3)(x+5)=0的解吗?
(x-3)(x+5)=0
解:x-3=0或x+5=0
所以x1=3,x2=-5.
①
②
上述解法中,由①到②的过程,不是用开平方降次,而是先因式分解,使方程化为两个一次的乘积等于0的形式,再使这两个一次式分别等于0,从而实现降次.
这种解一元二次方程的方法叫做因式分解法.
例1.解下列方程:
解:因式分解,得
于是得
x-2=0或x+1=0,
x1=2,x2=-1.
解:移项、合并同类项,得
因式分解,得
(2x+1)(2x-1)=0.
于是得
2x+1=0或2x-1=0,
(x-2)(x+1)=0.
可以试用多种方法解本例中的两个方程.
例1.解下列方程:
解:方程化为 x2-x-2=0
a=1,b=-1,c=-2
即 x1=2,x2=-1.
解:移项、合并同类项,得
系数化为1,得
直接开平方,得
Δ=b2-4ac
=(-1)2-4×1×(-2)=9>0
即
公式法
直接开平方法
配方法要先配方,再降次;通过配方法可以推出求根公式,公式法直接利用求根公式解方程;因式分解法要先使方程一边为两个一次因式相乘,另一边为0,再分别使各一次因式等于0. 配方法、公式法适用于所有一元二次方程,因式分解法在解某些一元二次方程时比较简便.
※解一元二次方程的基本思路是:将二次方程化为一次方程,即降次.
用因式分解法解下列方程:
解:x(x+1)=0
x=0或x+1=0
x1=0,x2=-1
解:
x=0或 x1=0,x2=
解:3x2-6x+3=0
x2-2x+1=0
(x-1)2=0
x1=x2=1
用因式分解法解下列方程:
解:(2x+11)(2x-11)=0 2x+11=0或2x-11=0
x1=-,x2=
解:3x(2x+1)-2(2x+1)=0 (2x+1)(3x-2)=0
2x+1=0或3x-2=0
x1=-,x2=
解:(x-4)2-(5-2x)2=0
(x-4+5-2x)(x-4-5+2x)=0
(1-x)(3x-9)=0
1-x=0或3x-9=0
x1=1,x2=3
例2.用适当的方法解方程:
【分析】方程一边以平方形式出现,另一边是常数,可直接开平方法.
【分析】二次项的系数为1,一次项的系数为偶数,可用配方法来解题较快.
解:x-1=±3
x-1=3或x-1=-3
∴x1=4,x2=-2
解:x2+2x+12=4+12
(x+1)2=5
∴x1= -1,x2= -1
x+1=±
例2.用适当的方法解方程:
【分析】方程左边变形后可以提取公因式,所以用因式分解法解答较快.
【分析】二次项的系数不为1,且不能直接开平方,也不能直接因式分解,所以适合公式法.
解:(x-2)2+2(x-2)=0
x=0或x-2=0
∴x1=0,x2=2
(x-2)(x-2+2)=0
x(x-2)=0
解:a=1,b=3,c=-4
即 x1=1,x2=-4.
Δ=b2-4ac=9+16=25>0
1.一般地,当一元二次方程一次项系数为0时(ax2+c=0),应选用直接开平方法;
2.若常数项为0(ax2+bx=0),应选用因式分解法;
3.若一次项系数和常数项都不为0 (ax2+bx+c=0),先化为一般式,看一边的整式是否容易因式分解,若容易,宜选用因式分解法,不然选用公式法;
4.不过当二次项系数是1,且一次项系数是偶数时,用配方法也较简单.
解法选择基本思路
用适当的方法解方程:
解:
3x-1=±2
∴x1=1,x2=-
解:x2+2x=48
(x+1)2=49
∴x1= -8,x2=
x+1=±
x2+2x+12=48+12
用适当的方法解方程:
解:a=2,b=-7,c=5
即 t1=,t2=1.
Δ=b2-4ac
=(-7)2-4×2×5=9>0
解:3(x-2)2=x2-4
∴x1=2,x2=4
(x-2)(3x-6-x-2)=0
3(x-2)2=(x+2)(x-2)
3(x-2)2-(x+2)(x-2)=0
(x-2)(2x-8)=0
1.一元二次方程(x-3)(x-5)=0的两根分别为( )
A.3,-5 B.3,5 C.-3,5 D.-3,-5
2.小华在解一元二次方程x2-x=0时,只得出一个根x=1,则被漏掉的一个根是( )
A.x=0 B.x=2 C.x=3 D.x=4
3.方程(x+1)(x-2)=x+1的解是( )
A.2 B.3 C.-1,2 D.-1,3
B
A
D
4.若分式 的值为零,则x的值是( )
A.3 B.-4 C.1或3 D.-1
A
5.一元二次方程x(x-5)=5-x的根是_______.
6.当x为_______时,代数式3x2的值与4x的值相等.
7.若(5x-6y)(x+y)=0, 则=______.
5和-1
0和
-1和
8.写出一个以-2和4为根的一元二次方程______________.
9.已知关于x的方程(x+a)(x-3)=0和x2-kx-3=0的根相同,则k=____,a=_____.
(x+2)(x-4)=0
2
1
【分析】由(x+a)(x-3)=0易得方程的一个根为x=3,
把x=3代入x2-kx-3=0得32-3k-3=0,
∴k=2得到方程x2-2x-3=0,
解得x1=-1,x2=3
∴-1+a=0,
∴a=1
① x2-3x+1=0; ②3x2-1=0; ③-3t2+t=0; ④x2-4x=2; ⑤2x2-x=0; ⑥5(m+2)2=8; ⑦3y2-y-1=0; ⑧2x2+4x-1=0; ⑨ (x-2)2=2(x-2).
适合运用直接开平方法 ;
适合运用因式分解法 ;
适合运用公式法 ;
适合运用配方法 .
⑥
①
②
③
④
⑤
⑦
⑧
⑨
10.填空:
达标检测
11.用适当的方法解方程:
解:(3x-2)2=(2x-1)2
∴x1=,x2=1
(3x-2+2x-1)(3x-2-2x+1)=0
(5x-3)(x-1)=0
(3x-2)2-(2x-1)2=0
解:
12.阅读材料:为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1视为一个整体,然后可设x2-1=y,则(x2-1)2=y2,原方程化为y2-5y+4=0①解得y1=1,y2=4.
当y=1时,x2-1=1.∴x2=2,∴x=±
当y=4时,x2-1=4.∴x2=5,∴x=±
∴原方程的解为x1=x2=-,x3=, x4=-
解答问题: (1)填空: 在由原方程得到方程①的过程中,利用_____法达到了降次的目的,体现了______的数学思想.
换元
转化
12.阅读材料:为解方程(x2-1)2-5(x2-1)+4=0,我们可以将x2-1视为一个整体,然后可设x2-1=y,则(x2-1)2=y2,原方程化为y2-5y+4=0①解得y1=1,y2=4.
当y=1时,x2-1=1.∴x2=2,∴x=±
当y=4时,x2-1=4.∴x2=5,∴x=±
∴原方程的解为x1=x2=-,x3=, x4=-
(2)解方程x4-5x2+6=0
解:设x2=y,则x4=y2
原方程化为y2-5y+6=0,解得y1=2,y2=3.
当y=2时,x2=2.∴x=±
当y=3时,x2=3.∴x=±
原方程的解为x1=x2=-,x3=, x4=-
一、概念:
二、原理:
三、基本步骤:
通过因式分解,将一个一元二次方程转化为两个一元一次方程来求解的方法叫做因式分解法.
如果a·b=0,那么a=0或b=0.
一移-----方程的右边=0;
二分-----方程的左边因式分解;
三化-----方程化为两个一元一次方程;
四解-----写出方程两个解;
简记歌诀:
右化零 左分解
两因式 各求解
1.一般地,当一元二次方程一次项系数为0时(ax2+c=0),应选用直接开平方法;
2.若常数项为0(ax2+bx=0),应选用因式分解法;
3.若一次项系数和常数项都不为0 (ax2+bx+c=0),先化为一般式,看一边的整式是否容易因式分解,若容易,宜选用因式分解法,不然选用公式法;
4.不过当二次项系数是1,且一次项系数是偶数时,用配方法也较简单.
解法选择基本思路
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
