【人教版九上数学优质课件】21.3.1 实际问题与一元二次方程(一)传播问题 课件(共27张PPT)
文档属性
| 名称 | 【人教版九上数学优质课件】21.3.1 实际问题与一元二次方程(一)传播问题 课件(共27张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 22:26:29 | ||
图片预览








文档简介
(共27张PPT)
九上数学同步优质课件
人教版九年级上册
实际问题与一元二次方程(一)
---传播问题
1.会分析实际问题(传播问题)中的数量关系并会列一元二次方程.(重点)
2.正确分析问题(传播问题)中的数量关系.(难点)
3.会找出实际问题(传播问题)中的相等关系并建模解决问题.
一、列方程解应用题的一般步骤是:
1.审:读懂题意,弄清题目中哪些是已知量,哪些是未知量,以及它们之 间的等量关系;
2.设:设未知数,语句要完整,有单位的要注明单位;
3.列:根据等量关系列出方程(组);
4.解:解所列方程(组);
5.验:检验所求方程(组)的解是否正确,是否符合题意;
6.答:答案也必需是完整的语句,注明单位.
二、列方程解应用题的关键是:
找等量关系
有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
第2轮
第1轮
注意:不要忽视病源A的二次传染.
第1轮传染后患病人数_______人;
特值分析法:
1.如果每轮每人传染2人.
第2轮传染后患病人数________________人.
(1+2)
1+2+(1+2)×2
病源A
设每轮传染中平均一个人传染了x个人.
第2轮
第1轮
第1轮传染后患病人数_______人;
第2轮传染后患病人数______________人.
[1+x+(1+x)x]
(1+x)
··
·
·
·
··
·
·
·
·
传染源人数 第1轮传染后的人数 第2轮传染后的人数
1
1+x=(1+x)1
1+x+x(1+x)=(1+x)2
规律发现
有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
x1= , x2= .
解方程,得
答:平均一个人传染了_____个人.
10
-12
(不合题意,舍去)
10
解:设每轮传染中平均一个人传染了x个人.
(1+x)2=121
注意:一元二次方程的解有可能不符合题意,所以一定要进行检验.
有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
如果按照这样的传染速度,三轮传染后有多少人患流感
第一轮传染后的人数 第二轮传染后的人数 第三轮传染后的人数 第n轮传染后的人数
如果按照这样的传染速度,三轮传染后有多少人患流感
三轮传染后:121+10×121=(10+1)3=113=1331(人)
n轮传染后:(10+1) n=11n(人)
n轮呢
规律发现
病源为1人时,如果每轮传染中平均一个人传染了x个人
(1+x)1
(1+x)2
(1+x)3
(1+x)n
例1.2020年3月,新冠肺炎疫情在中国已经得到有效控制,但在全球却开始持续蔓延,这是对人类的考验,将对全球造成巨大影响.新冠肺炎具有人传人的特性,若一人携带病毒,未进行有效隔离,经过两轮传染后共有256人患新冠肺炎,求每轮传染中平均每个人传染了几个人?
解:设每轮传染中平均每个人传染了x个人,
根据题意,得:(x+1)2=256,
直接开平方得x+1=±16,
解得x1=15,x2=-17,
经检验都是原方程的根,但x2=-17<0不符合实际(舍去),
答:每轮传染中平均每个人传染了15个人.
流行病学中有一个叫做基本传染数R0的数字,简单来说,就是一个人在一个周期内会感染几个人,有一个人感染了新冠病毒,经过两个周期的传染后共有36人感染,求新冠病毒的基本传染数R0.
解:由题意知,在第一个周期后共有1+R0个人感染;第二个周期后共有1+R0+(1+R0)×R0个人感染.
∴可列方程1+R0+(1+R0)×R0=36
∴(1+R0)2=36
解得R0=5或R0=-7(舍去)
∴新冠病毒的基本传染数R0为5.
例2.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是91,每个支干长出多少小分支
主干
支干
支干
……
小分支
小分支
……
小分支
小分支
……
……
x
x
x
1
解:设每个支干长出x个小分支,
则 1+x+x2=91
即
解得,
x1=9,x2=-10(不合题意,舍去)
答:每个支干长出9个小分支.
1.在分析例1和例2中的数量关系时它们有何区别?
每个树枝只分裂一次,每名患者每轮都传染.
2.解决这类传播问题有什么经验和方法?
(1)审题,设元,列方程,解方程,检验,作答;
(2)可利用表格梳理数量关系;
(3)关注起始值、新增数量,找出变化规律.
传播问题
有2人患了流感,经过两轮传染后共有288人患了流感,每轮传染中平均一个人传染了几个人
设每轮传染中平均一个人传染了x个人.
第1轮传染后患病人数_______人;
第2轮传染后患病人数_________________人.
[2+2x+(2+2x)x]
(2+2x)
2(1+x)2
2(1+x)2=288
解得 x1=11,x2=-13.
(不合题意,舍去)
2(1+x)
答:每轮传染中平均一个人传染了11人.
第一轮传染后的人数 第二轮传染后的人数 第三轮传染后的人数 第n轮传染后的人数
规律发现
病源为n人时,如果每轮传染中平均一个人传染了x个人
n(1+x)1
n(1+x)2
病源为n人时,如果每轮传染中平均一个人传染了x个人
n(1+x)3
n(1+x)n
例3.在古代有一部落,15位族人外出狩猎回来,其中有5个人染上了瘟疫,经过两轮传染后部落里共有125个人染上了瘟疫,每轮传染中平均一个人传染了几个人?
解:设每轮传染中平均一个人传染了x个人.
根据题意,列出方程
5+5x+x(5+5x)=125,
整理得 5(1+x)2=125
解得 x1=4,x2=-6(不合题意,舍去)
答:每轮传染中平均一个人传染了4个人.
某种病毒传播速度非常快,如果最初有两个人感染这种病毒,经两轮传播后,就有五十个人被感染,求每轮传播中平均一个人会传染给几个人?若病毒得不到有效控制,三轮传播后将有多少人被感染?
解:设每轮传播中平均一个人会传染给x个人,
根据题意列方程: 2+2x+x(2+2x)=50,
整理得:2(1+x)2=50,
解得:x1=4,x2=-6.(不合题意,舍去),
∴50×(1+4)=250(人).
答:每轮传播中平均一个人会传染给4个人,若病毒得不到有效控制,三轮传播后将有250人被感染.
建立一元二次方程模型
实际问题
分析数量关系
设未知数
实际问题的解
解一元二次方程
一元二次方程的根
检 验
运用一元二次方程模型解决实际问题的步骤有哪些?
达标检测
D
1.有一人患了流感,经过两轮传染后,共有121人患了流感,每轮传染中平均每人传染了x个人,下列结论错误的是( ).
A.1轮后有(x+1)个人患了流感
B.第2轮又增加x(x+1)个人患流感
C.依题意可得方程(x+1)2=121
D.不考虑其他因素经过三轮一共会有1210人感染
达标检测
2.有两名流感病人,如果每轮传播中平均一个病人传染的人数相同,为了使两轮传播后,流感病人总数不超过288人,则每轮传播中平均一个病人传染的人数不能超过( )人.
A.11 B.10 C.9 D.8
A
3.在某次冠状病毒感染中,有3只动物被感染,后来经过两轮感染后共有363只动物被感染.若每轮感染中平均一只动物会感染x只动物,则下面所列方程正确的是( )
A.3x(x+1)=363 B.3+3x+3x2=363
C.3(1+x)2=363 D.3+3(1+x)+3(1+x)2=363
C
4.某树主干长出x根枝干,每个枝干又长出x根小分支,若主干、枝干和小分支总数共133根,则主干长出枝干的根数x为______.
5.已知3人患流感,经过两轮传染后,患流感总人数为108人,则平均每人每轮感染_____个人.
11
5
6.某种电脑病毒传播速度非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?
解:设平均一台手机会感染x台手机,依题意得: 1+x+x(1+x)=81,即(1+x)2=81.
解得 x1=8,x2=-10(不合题意,舍去).
∴x=8.
3轮感染后,被感染的电脑数为(1+x)3=93=729>700.
答:平均一台手机会感染8台手机; 3轮感染后,被感染的手机会超过700台.
第一轮传染后的人数 第二轮传染后的人数 第三轮传染后的人数 第n轮传染后的人数
1.病源为1人时,如果每轮传染中平均一个人传染了x个人
(1+x)1
(1+x)2
(1+x)3
(1+x)n
第一轮传染后的人数 第二轮传染后的人数 第三轮传染后的人数 第n轮传染后的人数
2.病源为n人时,如果每轮传染中平均一个人传染了x个人
n(1+x)1
n(1+x)2
n(1+x) 3
n(1+x)n
建立一元二次方程模型
实际问题
分析数量关系
设未知数
实际问题的解
解一元二次方程
一元二次方程的根
检 验
运用一元二次方程模型解决实际问题的步骤有哪些?
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步优质课件
人教版九年级上册
实际问题与一元二次方程(一)
---传播问题
1.会分析实际问题(传播问题)中的数量关系并会列一元二次方程.(重点)
2.正确分析问题(传播问题)中的数量关系.(难点)
3.会找出实际问题(传播问题)中的相等关系并建模解决问题.
一、列方程解应用题的一般步骤是:
1.审:读懂题意,弄清题目中哪些是已知量,哪些是未知量,以及它们之 间的等量关系;
2.设:设未知数,语句要完整,有单位的要注明单位;
3.列:根据等量关系列出方程(组);
4.解:解所列方程(组);
5.验:检验所求方程(组)的解是否正确,是否符合题意;
6.答:答案也必需是完整的语句,注明单位.
二、列方程解应用题的关键是:
找等量关系
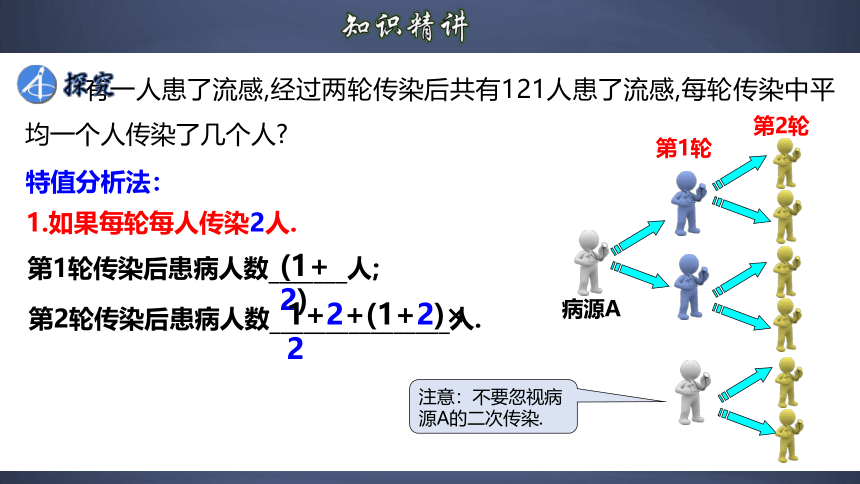
有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
第2轮
第1轮
注意:不要忽视病源A的二次传染.
第1轮传染后患病人数_______人;
特值分析法:
1.如果每轮每人传染2人.
第2轮传染后患病人数________________人.
(1+2)
1+2+(1+2)×2
病源A
设每轮传染中平均一个人传染了x个人.
第2轮
第1轮
第1轮传染后患病人数_______人;
第2轮传染后患病人数______________人.
[1+x+(1+x)x]
(1+x)
··
·
·
·
··
·
·
·
·
传染源人数 第1轮传染后的人数 第2轮传染后的人数
1
1+x=(1+x)1
1+x+x(1+x)=(1+x)2
规律发现
有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
x1= , x2= .
解方程,得
答:平均一个人传染了_____个人.
10
-12
(不合题意,舍去)
10
解:设每轮传染中平均一个人传染了x个人.
(1+x)2=121
注意:一元二次方程的解有可能不符合题意,所以一定要进行检验.
有一人患了流感,经过两轮传染后共有121人患了流感,每轮传染中平均一个人传染了几个人
如果按照这样的传染速度,三轮传染后有多少人患流感
第一轮传染后的人数 第二轮传染后的人数 第三轮传染后的人数 第n轮传染后的人数
如果按照这样的传染速度,三轮传染后有多少人患流感
三轮传染后:121+10×121=(10+1)3=113=1331(人)
n轮传染后:(10+1) n=11n(人)
n轮呢
规律发现
病源为1人时,如果每轮传染中平均一个人传染了x个人
(1+x)1
(1+x)2
(1+x)3
(1+x)n
例1.2020年3月,新冠肺炎疫情在中国已经得到有效控制,但在全球却开始持续蔓延,这是对人类的考验,将对全球造成巨大影响.新冠肺炎具有人传人的特性,若一人携带病毒,未进行有效隔离,经过两轮传染后共有256人患新冠肺炎,求每轮传染中平均每个人传染了几个人?
解:设每轮传染中平均每个人传染了x个人,
根据题意,得:(x+1)2=256,
直接开平方得x+1=±16,
解得x1=15,x2=-17,
经检验都是原方程的根,但x2=-17<0不符合实际(舍去),
答:每轮传染中平均每个人传染了15个人.
流行病学中有一个叫做基本传染数R0的数字,简单来说,就是一个人在一个周期内会感染几个人,有一个人感染了新冠病毒,经过两个周期的传染后共有36人感染,求新冠病毒的基本传染数R0.
解:由题意知,在第一个周期后共有1+R0个人感染;第二个周期后共有1+R0+(1+R0)×R0个人感染.
∴可列方程1+R0+(1+R0)×R0=36
∴(1+R0)2=36
解得R0=5或R0=-7(舍去)
∴新冠病毒的基本传染数R0为5.
例2.某种植物的主干长出若干数目的支干,每个支干又长出同样数目的小分支,主干,支干和小分支的总数是91,每个支干长出多少小分支
主干
支干
支干
……
小分支
小分支
……
小分支
小分支
……
……
x
x
x
1
解:设每个支干长出x个小分支,
则 1+x+x2=91
即
解得,
x1=9,x2=-10(不合题意,舍去)
答:每个支干长出9个小分支.
1.在分析例1和例2中的数量关系时它们有何区别?
每个树枝只分裂一次,每名患者每轮都传染.
2.解决这类传播问题有什么经验和方法?
(1)审题,设元,列方程,解方程,检验,作答;
(2)可利用表格梳理数量关系;
(3)关注起始值、新增数量,找出变化规律.
传播问题
有2人患了流感,经过两轮传染后共有288人患了流感,每轮传染中平均一个人传染了几个人
设每轮传染中平均一个人传染了x个人.
第1轮传染后患病人数_______人;
第2轮传染后患病人数_________________人.
[2+2x+(2+2x)x]
(2+2x)
2(1+x)2
2(1+x)2=288
解得 x1=11,x2=-13.
(不合题意,舍去)
2(1+x)
答:每轮传染中平均一个人传染了11人.
第一轮传染后的人数 第二轮传染后的人数 第三轮传染后的人数 第n轮传染后的人数
规律发现
病源为n人时,如果每轮传染中平均一个人传染了x个人
n(1+x)1
n(1+x)2
病源为n人时,如果每轮传染中平均一个人传染了x个人
n(1+x)3
n(1+x)n
例3.在古代有一部落,15位族人外出狩猎回来,其中有5个人染上了瘟疫,经过两轮传染后部落里共有125个人染上了瘟疫,每轮传染中平均一个人传染了几个人?
解:设每轮传染中平均一个人传染了x个人.
根据题意,列出方程
5+5x+x(5+5x)=125,
整理得 5(1+x)2=125
解得 x1=4,x2=-6(不合题意,舍去)
答:每轮传染中平均一个人传染了4个人.
某种病毒传播速度非常快,如果最初有两个人感染这种病毒,经两轮传播后,就有五十个人被感染,求每轮传播中平均一个人会传染给几个人?若病毒得不到有效控制,三轮传播后将有多少人被感染?
解:设每轮传播中平均一个人会传染给x个人,
根据题意列方程: 2+2x+x(2+2x)=50,
整理得:2(1+x)2=50,
解得:x1=4,x2=-6.(不合题意,舍去),
∴50×(1+4)=250(人).
答:每轮传播中平均一个人会传染给4个人,若病毒得不到有效控制,三轮传播后将有250人被感染.
建立一元二次方程模型
实际问题
分析数量关系
设未知数
实际问题的解
解一元二次方程
一元二次方程的根
检 验
运用一元二次方程模型解决实际问题的步骤有哪些?
达标检测
D
1.有一人患了流感,经过两轮传染后,共有121人患了流感,每轮传染中平均每人传染了x个人,下列结论错误的是( ).
A.1轮后有(x+1)个人患了流感
B.第2轮又增加x(x+1)个人患流感
C.依题意可得方程(x+1)2=121
D.不考虑其他因素经过三轮一共会有1210人感染
达标检测
2.有两名流感病人,如果每轮传播中平均一个病人传染的人数相同,为了使两轮传播后,流感病人总数不超过288人,则每轮传播中平均一个病人传染的人数不能超过( )人.
A.11 B.10 C.9 D.8
A
3.在某次冠状病毒感染中,有3只动物被感染,后来经过两轮感染后共有363只动物被感染.若每轮感染中平均一只动物会感染x只动物,则下面所列方程正确的是( )
A.3x(x+1)=363 B.3+3x+3x2=363
C.3(1+x)2=363 D.3+3(1+x)+3(1+x)2=363
C
4.某树主干长出x根枝干,每个枝干又长出x根小分支,若主干、枝干和小分支总数共133根,则主干长出枝干的根数x为______.
5.已知3人患流感,经过两轮传染后,患流感总人数为108人,则平均每人每轮感染_____个人.
11
5
6.某种电脑病毒传播速度非常快,如果一台电脑被感染,经过两轮感染后就会有81台电脑被感染.请你用学过的知识分析,每轮感染中平均一台电脑会感染几台电脑?若病毒得不到有效控制,3轮感染后,被感染的电脑会不会超过700台?
解:设平均一台手机会感染x台手机,依题意得: 1+x+x(1+x)=81,即(1+x)2=81.
解得 x1=8,x2=-10(不合题意,舍去).
∴x=8.
3轮感染后,被感染的电脑数为(1+x)3=93=729>700.
答:平均一台手机会感染8台手机; 3轮感染后,被感染的手机会超过700台.
第一轮传染后的人数 第二轮传染后的人数 第三轮传染后的人数 第n轮传染后的人数
1.病源为1人时,如果每轮传染中平均一个人传染了x个人
(1+x)1
(1+x)2
(1+x)3
(1+x)n
第一轮传染后的人数 第二轮传染后的人数 第三轮传染后的人数 第n轮传染后的人数
2.病源为n人时,如果每轮传染中平均一个人传染了x个人
n(1+x)1
n(1+x)2
n(1+x) 3
n(1+x)n
建立一元二次方程模型
实际问题
分析数量关系
设未知数
实际问题的解
解一元二次方程
一元二次方程的根
检 验
运用一元二次方程模型解决实际问题的步骤有哪些?
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
