【人教版九上数学优质课件】21.3.2 实际问题与一元二次方程(二)平均变化率问题 课件(共24张PPT)
文档属性
| 名称 | 【人教版九上数学优质课件】21.3.2 实际问题与一元二次方程(二)平均变化率问题 课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 22:27:55 | ||
图片预览








文档简介
(共24张PPT)
九上数学同步优质课件
人教版九年级上册
实际问题与一元二次方程(二)
---平均变化率问题
1.会分析实际问题(平均变化率问题)中的数量关系并会列一元二次方程.(重点)
2.正确分析问题(平均变化率问题)中的数量关系.(难点)
3.会找出实际问题(平均变化率问题)中的相等关系并建模解决问题.
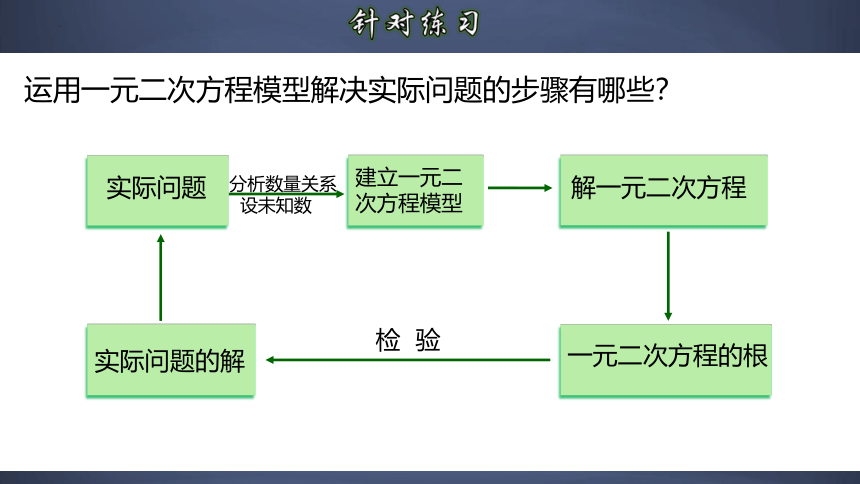
建立一元二次方程模型
实际问题
分析数量关系
设未知数
实际问题的解
解一元二次方程
一元二次方程的根
检 验
运用一元二次方程模型解决实际问题的步骤有哪些?
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
分析:
甲种药品成本的年平均下降额为:
乙种药品成本的年平均下降额为:
(5000-3000)÷2=1000(元)
(6000-3600)÷2=1200(元)
显然,乙种药品成本的年平均下降额较大.但是,年平均下降额(元)不等同于年平均下降率(百分数).
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
解:设甲种药品成本的年平均下降率为x,则一年后甲种药品成本为___________元,两年后甲种药品成本为___________元,根据题意,列出方程
5000(1-x)
5000(1-x)2
5000(1-x)2=3000
解得 x1≈0.225,x2≈1.775(不合题意,舍去)
答:根据问题的实际意义,甲种药品成本的年平均下降率约为22.5%.
强调:下降率不可为负,且不大于1.
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
算一算:乙种药品成本的年平均下降率是多少?
比较:两种药品成本的年平均下降率.
类似于甲种药品成本年平均下降率的计算,根据题意,列出方程 6000(1-y)2=3600
解得乙种药品成本年平均下降率约为22.5%.
(相同)
经过计算,你能得出什么结论?成本下降额大的药品,它的成本下降率一定也大吗?应怎样全面地比较几个对象的变化状况?
成本下降额大的产品,其成本下降率不一定大.成本下降额表示绝对变化量,成本下降率表示相对变化量,两者兼顾才能全面比较对象的变化状况.
方法总结:
类似地 这种增长率的问题在实际生活中普遍存在,有一定的模式.若平均增长(或降低)百分率为x,增长(或降低)前的是a,增长(或降低)n次后的量是b,则它们的数量关系可表示为
a(1±x) n=b(其中增长取“+”,降低取“-”)
解:设这个增长率为x.根据题意,得
答:这个增长率为50%.
200+200(1+x)+200(1+x)2=950
整理方程,得
4x2+12x-7=0,
解这个方程得
x1=-3.5(舍去),x2=0.5.
例1.某公司去年的各项经营中,一月份的营业额为200万元,一月、二月、三月的营业额共950万元,如果平均每月营业额的增长率相同,求这个增长率.
强调:增长率不可为负,但可以超过1.
某农机厂四月份生产零件50万个,第二季度共生产零件182万个,求该厂五、六月份平均每月的增长率.
解:设该厂五、六月份平均每月的增长率为x,依题意得:
50+50(1+x)+50(1+x)2=182
整理,得50x2+150x-32=0
解方程,得x1=0.2,x2=-3.2(不合题意,舍去)
答:该厂五、六月份平均每月的增长率为20%.
例2.某药品经两次降价,零售价降为原来的一半.已知两次降价的百分率一样,求每次降价的百分率.(精确到0.1%)
解:设原价为1个单位,每次降价的百分率为 x.
根据题意,得
解这个方程,得
答:每次降价的百分率为29.3%.
某药品两次升价,零售价升为原来的 1.2倍,已知两次升价的百分率一样,求每次升价的百分率(精确到0.1%)
解,设原价为a元,每次升价的百分率为x ,
根据题意,得
解这个方程,得
由于升价的百分率不可能是负数,
所以 (不合题意,舍去)
答:每次升价的百分率为9.5%.
例3.2022年北京冬奥会和冬残奥会的吉祥物冰墩墩和雪容融深受国内外广大朋友的喜爱,北京奥组委会官方也推出了许多吉祥物的周边产品.现有以下两款:如图的“冰墩墩”和“雪容融”.已知购买3个冰墩墩和2个雪容融需要560元;购买1个冰墩墩和3个雪容融需要420元;
(1)请问冰墩墩和雪容融每个的售价分别是多少元?
解:设冰墩墩每个的售价是x元,雪容融每个的售价是y元,根据题意得:
解得
所以,冰墩墩每个的售价是120元,雪容融每个的售价是100元.
(2)某特许零售店发现该“冰墩墩”的销售非常火爆.据统计,该店2021年10月的销量为1万件,2021年12月的销量为1.21万件.若该店“冰墩墩”销量的月平均增长率保持不变,求2022年1月销售该“冰墩墩”的收入多少万元?
解:设月平均增长率为a,则11月份的销售量为(1+a),12月份的销售量为(1+a)2,
根据题意,得:1×(1+a)2=1.21,
解得a1=0.1=10%,a2=-2.1 (不合题意,舍去),
1.21×(1+10%)×120=159.72(万元),
所以,2022年1月销售该“冰墩墩”的收入为159.72万元.
1.某商品原售价289元,经过连续两次降价后售价为256元,设平均每次降价的百分率为x,则下面所列方程中正确的是( )
A.256(1+x)2=289 B.289(1-x)2=256
C.289(1-2x)=256 D.256(1-2x)=289
2.某商场的营业额2011年比2010年上升10%,2012年比2011年又上升10%,而2013年和2014年 连续两年平均每年比上一年降低10%,那么2014年的营业额比2010年的营业额( )
A.降低了 B.没有变化 C.上升了 D.无法确定
B
A
3.截至2022年3月31日,电影《长津湖之水门桥》票房已突破37亿元.第一天票房约6亿元,三天后票房累计总收入达24亿元,如果第二天,第三天票房收入按相同的增长率增长,增长率设为x.则可列方程为( )
A. B.
C. D.
D
4.某商店6月份的利润是2.5万元,要使8月份的利润达到3.6万元,这两个月的月平均增长率是多少?
解:设这两个月的月平均增长率是x.根据题意,列出方程
2.5(1+x)2=3.6
解方程,得 x1=0.2,x2=-2.2(不合题意,舍去)
答:这两个月的月平均增长率为20%.
5.今年三月,新冠肺炎疫情再次波及长沙,某社区超市将原来每瓶售价为20元的免洗消毒液经过两次降价后(每次降价的百分率相同),以每瓶16.2元出售支持社区防疫.
(1)求每次降价的百分率;
(2)商家库存的1000瓶免洗消毒液每瓶进价为15元,仓储、人工等成本大约共1500元,计划通过以上两次降价方式全部售出后确保不亏损,那么第一次降价至少售出多少瓶后,方可进行第二次降价?
(1)解:设每次降价的百分率为x,则20(1-x)2=16.2,
解得x1=0.1,x2=1.9(舍去)
答:每次降价的百分率为10%.
(2)商家库存的1000瓶免洗消毒液每瓶进价为15元,仓储、人工等成本大约共1500元,计划通过以上两次降价方式全部售出后确保不亏损,那么第一次降价至少售出多少瓶后,方可进行第二次降价?
解:由(1)知第一次降价后的售价为18元,设第一次降价销售y瓶,根据题意:
(18-15)y+(16.2-15)(1000-y)≥1500
解得y≥≈166.7
答:第一次降价至少售出167瓶后,方可进行第二次降价.
平均变化率问题
1.增长率问题
a(1+x)2=b
2.降低率问题
(其中a为降低前的量,x为降低率,2为降低次数,b为降低后的量.)
模型
(其中a为增长前的量,x为增长率,2为增长次数,b为增长后的量.)
模型
a(1-x)2=b
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步优质课件
人教版九年级上册
实际问题与一元二次方程(二)
---平均变化率问题
1.会分析实际问题(平均变化率问题)中的数量关系并会列一元二次方程.(重点)
2.正确分析问题(平均变化率问题)中的数量关系.(难点)
3.会找出实际问题(平均变化率问题)中的相等关系并建模解决问题.
建立一元二次方程模型
实际问题
分析数量关系
设未知数
实际问题的解
解一元二次方程
一元二次方程的根
检 验
运用一元二次方程模型解决实际问题的步骤有哪些?
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
分析:
甲种药品成本的年平均下降额为:
乙种药品成本的年平均下降额为:
(5000-3000)÷2=1000(元)
(6000-3600)÷2=1200(元)
显然,乙种药品成本的年平均下降额较大.但是,年平均下降额(元)不等同于年平均下降率(百分数).
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
解:设甲种药品成本的年平均下降率为x,则一年后甲种药品成本为___________元,两年后甲种药品成本为___________元,根据题意,列出方程
5000(1-x)
5000(1-x)2
5000(1-x)2=3000
解得 x1≈0.225,x2≈1.775(不合题意,舍去)
答:根据问题的实际意义,甲种药品成本的年平均下降率约为22.5%.
强调:下降率不可为负,且不大于1.
两年前生产1t甲种药品的成本是5000元,生产1t乙种药品的成本是6000元,随着生产技术的进步,现在生产1t甲种药品的成本是3000元,生产1t乙种药品的成本是3600元,哪种药品成本的年平均下降率较大?
算一算:乙种药品成本的年平均下降率是多少?
比较:两种药品成本的年平均下降率.
类似于甲种药品成本年平均下降率的计算,根据题意,列出方程 6000(1-y)2=3600
解得乙种药品成本年平均下降率约为22.5%.
(相同)
经过计算,你能得出什么结论?成本下降额大的药品,它的成本下降率一定也大吗?应怎样全面地比较几个对象的变化状况?
成本下降额大的产品,其成本下降率不一定大.成本下降额表示绝对变化量,成本下降率表示相对变化量,两者兼顾才能全面比较对象的变化状况.
方法总结:
类似地 这种增长率的问题在实际生活中普遍存在,有一定的模式.若平均增长(或降低)百分率为x,增长(或降低)前的是a,增长(或降低)n次后的量是b,则它们的数量关系可表示为
a(1±x) n=b(其中增长取“+”,降低取“-”)
解:设这个增长率为x.根据题意,得
答:这个增长率为50%.
200+200(1+x)+200(1+x)2=950
整理方程,得
4x2+12x-7=0,
解这个方程得
x1=-3.5(舍去),x2=0.5.
例1.某公司去年的各项经营中,一月份的营业额为200万元,一月、二月、三月的营业额共950万元,如果平均每月营业额的增长率相同,求这个增长率.
强调:增长率不可为负,但可以超过1.
某农机厂四月份生产零件50万个,第二季度共生产零件182万个,求该厂五、六月份平均每月的增长率.
解:设该厂五、六月份平均每月的增长率为x,依题意得:
50+50(1+x)+50(1+x)2=182
整理,得50x2+150x-32=0
解方程,得x1=0.2,x2=-3.2(不合题意,舍去)
答:该厂五、六月份平均每月的增长率为20%.
例2.某药品经两次降价,零售价降为原来的一半.已知两次降价的百分率一样,求每次降价的百分率.(精确到0.1%)
解:设原价为1个单位,每次降价的百分率为 x.
根据题意,得
解这个方程,得
答:每次降价的百分率为29.3%.
某药品两次升价,零售价升为原来的 1.2倍,已知两次升价的百分率一样,求每次升价的百分率(精确到0.1%)
解,设原价为a元,每次升价的百分率为x ,
根据题意,得
解这个方程,得
由于升价的百分率不可能是负数,
所以 (不合题意,舍去)
答:每次升价的百分率为9.5%.
例3.2022年北京冬奥会和冬残奥会的吉祥物冰墩墩和雪容融深受国内外广大朋友的喜爱,北京奥组委会官方也推出了许多吉祥物的周边产品.现有以下两款:如图的“冰墩墩”和“雪容融”.已知购买3个冰墩墩和2个雪容融需要560元;购买1个冰墩墩和3个雪容融需要420元;
(1)请问冰墩墩和雪容融每个的售价分别是多少元?
解:设冰墩墩每个的售价是x元,雪容融每个的售价是y元,根据题意得:
解得
所以,冰墩墩每个的售价是120元,雪容融每个的售价是100元.
(2)某特许零售店发现该“冰墩墩”的销售非常火爆.据统计,该店2021年10月的销量为1万件,2021年12月的销量为1.21万件.若该店“冰墩墩”销量的月平均增长率保持不变,求2022年1月销售该“冰墩墩”的收入多少万元?
解:设月平均增长率为a,则11月份的销售量为(1+a),12月份的销售量为(1+a)2,
根据题意,得:1×(1+a)2=1.21,
解得a1=0.1=10%,a2=-2.1 (不合题意,舍去),
1.21×(1+10%)×120=159.72(万元),
所以,2022年1月销售该“冰墩墩”的收入为159.72万元.
1.某商品原售价289元,经过连续两次降价后售价为256元,设平均每次降价的百分率为x,则下面所列方程中正确的是( )
A.256(1+x)2=289 B.289(1-x)2=256
C.289(1-2x)=256 D.256(1-2x)=289
2.某商场的营业额2011年比2010年上升10%,2012年比2011年又上升10%,而2013年和2014年 连续两年平均每年比上一年降低10%,那么2014年的营业额比2010年的营业额( )
A.降低了 B.没有变化 C.上升了 D.无法确定
B
A
3.截至2022年3月31日,电影《长津湖之水门桥》票房已突破37亿元.第一天票房约6亿元,三天后票房累计总收入达24亿元,如果第二天,第三天票房收入按相同的增长率增长,增长率设为x.则可列方程为( )
A. B.
C. D.
D
4.某商店6月份的利润是2.5万元,要使8月份的利润达到3.6万元,这两个月的月平均增长率是多少?
解:设这两个月的月平均增长率是x.根据题意,列出方程
2.5(1+x)2=3.6
解方程,得 x1=0.2,x2=-2.2(不合题意,舍去)
答:这两个月的月平均增长率为20%.
5.今年三月,新冠肺炎疫情再次波及长沙,某社区超市将原来每瓶售价为20元的免洗消毒液经过两次降价后(每次降价的百分率相同),以每瓶16.2元出售支持社区防疫.
(1)求每次降价的百分率;
(2)商家库存的1000瓶免洗消毒液每瓶进价为15元,仓储、人工等成本大约共1500元,计划通过以上两次降价方式全部售出后确保不亏损,那么第一次降价至少售出多少瓶后,方可进行第二次降价?
(1)解:设每次降价的百分率为x,则20(1-x)2=16.2,
解得x1=0.1,x2=1.9(舍去)
答:每次降价的百分率为10%.
(2)商家库存的1000瓶免洗消毒液每瓶进价为15元,仓储、人工等成本大约共1500元,计划通过以上两次降价方式全部售出后确保不亏损,那么第一次降价至少售出多少瓶后,方可进行第二次降价?
解:由(1)知第一次降价后的售价为18元,设第一次降价销售y瓶,根据题意:
(18-15)y+(16.2-15)(1000-y)≥1500
解得y≥≈166.7
答:第一次降价至少售出167瓶后,方可进行第二次降价.
平均变化率问题
1.增长率问题
a(1+x)2=b
2.降低率问题
(其中a为降低前的量,x为降低率,2为降低次数,b为降低后的量.)
模型
(其中a为增长前的量,x为增长率,2为增长次数,b为增长后的量.)
模型
a(1-x)2=b
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
