【人教版九上数学优质课件】21.3.3 实际问题与一元二次方程(三)握手类型问题 课件(共22张PPT)
文档属性
| 名称 | 【人教版九上数学优质课件】21.3.3 实际问题与一元二次方程(三)握手类型问题 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 22:29:52 | ||
图片预览







文档简介
(共22张PPT)
九上数学同步优质课件
人教版九年级上册
实际问题与一元二次方程(三)
---握手类型问题
1.会分析实际问题(握手类型问题)中的数量关系并会列一元二次方程.(重点)
2.正确分析问题(握手类型问题)中的数量关系.(难点)
3.会找出实际问题(握手类型问题)中的相等关系并建模解决问题.
你若和班级所有同学都握手,你需握手多少次?
如果班级共有50个学生,你和其余同学握手. 一共要握手____次.
49
1.如果班级共有x个学生,一个学生去和其余同学握手. 这个同学要握手________次.
( x - 1 )
3.每两个学生握手一次,现有x个学生一共要握手_______次.
2.如果每个学生都去和其余同学握手. 我们共握手__________次.
x( x - 1 )
思考下列问题:
注意:两个人只需握一次手,所以有一半的次数是重复的.
老师所教的班级中,每两个学生都握手一次,全班学生一共握手780次,那么谁能计算出老师所教的班级共有多少名学生?(设老师所教班级有x个人)
思考:
1.则每个人与 人握手;
2.全班共握手 次(用含有x的式子表示);
3.依题意,可列方程为:___________.
( x - 1 )
握手问题模型:
有n人,每两人都握手一次手,握手的总次数为
生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组共互赠了182件,那么全组有多少名同学?(设全组有x名同学)
思考:
1.则每个人会送出 件标本;
2.全组共送出 件(用含有x的式
子表示);
3.依题意,可列方程为:___________.
( x - 1 )
注意:互赠礼物是相互的.
互赠礼物问题模型:
有n人,互赠礼物,互赠的总件数为
★握手问题模型:
有n人,每两人都握手一次手,握手的总次数为 次.
★互赠礼物问题模型:
有n人,互赠礼物,互赠的总件数为 件.
生活中还有哪些问题与“握手问题”、“互赠礼物问题”类似呢?
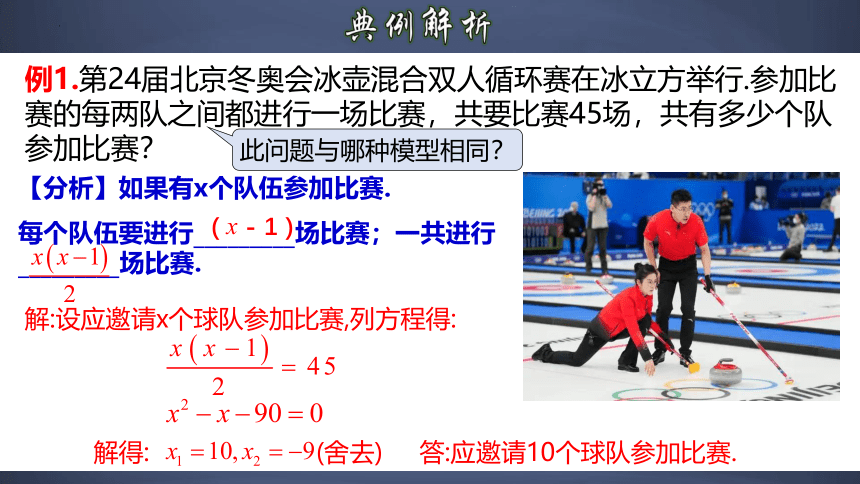
例1.第24届北京冬奥会冰壶混合双人循环赛在冰立方举行.参加比赛的每两队之间都进行一场比赛,共要比赛45场,共有多少个队参加比赛?
解:设应邀请x个球队参加比赛,列方程得:
解得:
(舍去)
答:应邀请10个球队参加比赛.
此问题与哪种模型相同?
【分析】如果有x个队伍参加比赛.
每个队伍要进行_________场比赛;一共进行_________场比赛.
( x - 1 )
例2.2021-2022赛季中国男子篮球职业联赛(CBA),继续采用双循环制(每两队之间都进行两场比赛),总比赛场数为552场.求有多少支队伍参加比赛?
此问题与哪种模型相同?
解:设应邀请x个球队参加比赛,列方程得:
解得:
(舍去)
答:有24个球队参加比赛.
【分析】如果有x个队伍参加比赛.
每个队伍要进行_________场比赛;一共进行_________场比赛.
( x - 1 )
例3.2019女排世界杯于9月14月至29日在日本举行,赛制为单循环比赛(即每两个队之间比赛一场)一共比赛66场,中国女排以全胜成绩卫冕世界杯冠军为国庆70周年献上大礼,则中国队在本届世界杯比赛中连胜多少场比赛?
【分析】设中国队在本届世界杯比赛中连胜
____场,则共有_______支队伍参加比赛.
( x+1 )
x
解:设中国队在本届世界杯比赛中连胜x场,列方程得:
解得:
(舍去)
答:连胜11场比赛.
此问题与哪种模型相同?
例4.白云航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了10条航线,则这个航空公司共有几个飞机场?
此问题与哪种模型相同?
【分析】设共有x个飞机场,每个飞机场都要与其余的飞机场开辟一条航行,但两个飞机场之间只开通一条航线.
解:设共有x个飞机场,列方程得:
解得:
(舍去)
答:这个航空公司共有5个飞机场.
1.距考试还有20天的时间,为鼓舞干劲,老师要求班上每一名同学要给同组的其他同学写一份拼搏进取的留言,小明所在的小组共写了30份留言,该小组共有( )
A.7人 B.6人 C.5人 D.4人
B
2.中国--东盟博览会、商务与投资峰会期间,在某个商品交易会上,参加一次商品交易会的每两家公司之间都签订了一份合同,所有公司共签订了450份合同.设共有x家公司参加商品交易会,根据题意,可列方程为( )
A.
B.
C.
D.
D
3.新冠肺炎全球蔓延,为防控疫情,做到有“礼”有“距”,“碰肘礼”逐渐流行起来.某次会议上,每两个参加会议的人都相互一次“碰肘礼”,经统计所有人共碰肘36次,则这次会议到会人数是_____人.
9
10
4.在小华的某个微信群中,若每人给其他成员都发一个红包,该微信群共发了90个红包,那么这个微信群共有_____人.
5.九年级(7)班文学小组在举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,全组共互赠了132本图书,如果设全组共有x名同学,依题意,可列出的方程是______________.
x(x 1)=132
6.某校在冬运会中,其中一项为乒乓球赛,赛制为参赛的每两个人之间都要比赛一场,根据胜场积分确定排名,由于场地和时间等条件,赛程安排3天,每天安排15场比赛,求共有多少学生参加了冬运会乒乓球赛?
解:设有x名学生参加了乒乓球赛,则
,
解得: (不符合实际,舍去),
答:共有10名学生参加了乒乓球赛.
7.若在直角∠AOB的内部由顶点O引出m条射线(不含OA、OB边),角的总数能否是20个,为什么?
解:不可能,理由如下:
设从点O共引出m条射线,若共有20个角,
则有: ,
解得: (负值舍去),
∴ ,与m为正整数矛盾,所以不可能有20个角.
握手问题
1.单循环赛事
2.打电话问题
3.图形规律问题
双循环赛事问题
互赠礼物问题
★握手问题模型:
有n人,每两人都握手一次手,握手的总次数为 次.
★互赠礼物问题模型:
有n人,互赠礼物,互赠的总件数为 件.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步优质课件
人教版九年级上册
实际问题与一元二次方程(三)
---握手类型问题
1.会分析实际问题(握手类型问题)中的数量关系并会列一元二次方程.(重点)
2.正确分析问题(握手类型问题)中的数量关系.(难点)
3.会找出实际问题(握手类型问题)中的相等关系并建模解决问题.
你若和班级所有同学都握手,你需握手多少次?
如果班级共有50个学生,你和其余同学握手. 一共要握手____次.
49
1.如果班级共有x个学生,一个学生去和其余同学握手. 这个同学要握手________次.
( x - 1 )
3.每两个学生握手一次,现有x个学生一共要握手_______次.
2.如果每个学生都去和其余同学握手. 我们共握手__________次.
x( x - 1 )
思考下列问题:
注意:两个人只需握一次手,所以有一半的次数是重复的.
老师所教的班级中,每两个学生都握手一次,全班学生一共握手780次,那么谁能计算出老师所教的班级共有多少名学生?(设老师所教班级有x个人)
思考:
1.则每个人与 人握手;
2.全班共握手 次(用含有x的式子表示);
3.依题意,可列方程为:___________.
( x - 1 )
握手问题模型:
有n人,每两人都握手一次手,握手的总次数为
生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组共互赠了182件,那么全组有多少名同学?(设全组有x名同学)
思考:
1.则每个人会送出 件标本;
2.全组共送出 件(用含有x的式
子表示);
3.依题意,可列方程为:___________.
( x - 1 )
注意:互赠礼物是相互的.
互赠礼物问题模型:
有n人,互赠礼物,互赠的总件数为
★握手问题模型:
有n人,每两人都握手一次手,握手的总次数为 次.
★互赠礼物问题模型:
有n人,互赠礼物,互赠的总件数为 件.
生活中还有哪些问题与“握手问题”、“互赠礼物问题”类似呢?
例1.第24届北京冬奥会冰壶混合双人循环赛在冰立方举行.参加比赛的每两队之间都进行一场比赛,共要比赛45场,共有多少个队参加比赛?
解:设应邀请x个球队参加比赛,列方程得:
解得:
(舍去)
答:应邀请10个球队参加比赛.
此问题与哪种模型相同?
【分析】如果有x个队伍参加比赛.
每个队伍要进行_________场比赛;一共进行_________场比赛.
( x - 1 )
例2.2021-2022赛季中国男子篮球职业联赛(CBA),继续采用双循环制(每两队之间都进行两场比赛),总比赛场数为552场.求有多少支队伍参加比赛?
此问题与哪种模型相同?
解:设应邀请x个球队参加比赛,列方程得:
解得:
(舍去)
答:有24个球队参加比赛.
【分析】如果有x个队伍参加比赛.
每个队伍要进行_________场比赛;一共进行_________场比赛.
( x - 1 )
例3.2019女排世界杯于9月14月至29日在日本举行,赛制为单循环比赛(即每两个队之间比赛一场)一共比赛66场,中国女排以全胜成绩卫冕世界杯冠军为国庆70周年献上大礼,则中国队在本届世界杯比赛中连胜多少场比赛?
【分析】设中国队在本届世界杯比赛中连胜
____场,则共有_______支队伍参加比赛.
( x+1 )
x
解:设中国队在本届世界杯比赛中连胜x场,列方程得:
解得:
(舍去)
答:连胜11场比赛.
此问题与哪种模型相同?
例4.白云航空公司有若干个飞机场,每两个飞机场之间都开辟一条航线,一共开辟了10条航线,则这个航空公司共有几个飞机场?
此问题与哪种模型相同?
【分析】设共有x个飞机场,每个飞机场都要与其余的飞机场开辟一条航行,但两个飞机场之间只开通一条航线.
解:设共有x个飞机场,列方程得:
解得:
(舍去)
答:这个航空公司共有5个飞机场.
1.距考试还有20天的时间,为鼓舞干劲,老师要求班上每一名同学要给同组的其他同学写一份拼搏进取的留言,小明所在的小组共写了30份留言,该小组共有( )
A.7人 B.6人 C.5人 D.4人
B
2.中国--东盟博览会、商务与投资峰会期间,在某个商品交易会上,参加一次商品交易会的每两家公司之间都签订了一份合同,所有公司共签订了450份合同.设共有x家公司参加商品交易会,根据题意,可列方程为( )
A.
B.
C.
D.
D
3.新冠肺炎全球蔓延,为防控疫情,做到有“礼”有“距”,“碰肘礼”逐渐流行起来.某次会议上,每两个参加会议的人都相互一次“碰肘礼”,经统计所有人共碰肘36次,则这次会议到会人数是_____人.
9
10
4.在小华的某个微信群中,若每人给其他成员都发一个红包,该微信群共发了90个红包,那么这个微信群共有_____人.
5.九年级(7)班文学小组在举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,全组共互赠了132本图书,如果设全组共有x名同学,依题意,可列出的方程是______________.
x(x 1)=132
6.某校在冬运会中,其中一项为乒乓球赛,赛制为参赛的每两个人之间都要比赛一场,根据胜场积分确定排名,由于场地和时间等条件,赛程安排3天,每天安排15场比赛,求共有多少学生参加了冬运会乒乓球赛?
解:设有x名学生参加了乒乓球赛,则
,
解得: (不符合实际,舍去),
答:共有10名学生参加了乒乓球赛.
7.若在直角∠AOB的内部由顶点O引出m条射线(不含OA、OB边),角的总数能否是20个,为什么?
解:不可能,理由如下:
设从点O共引出m条射线,若共有20个角,
则有: ,
解得: (负值舍去),
∴ ,与m为正整数矛盾,所以不可能有20个角.
握手问题
1.单循环赛事
2.打电话问题
3.图形规律问题
双循环赛事问题
互赠礼物问题
★握手问题模型:
有n人,每两人都握手一次手,握手的总次数为 次.
★互赠礼物问题模型:
有n人,互赠礼物,互赠的总件数为 件.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
