【人教版九上数学优质课件】21.4 一元二次方程 章末小结 课件(共47张PPT)
文档属性
| 名称 | 【人教版九上数学优质课件】21.4 一元二次方程 章末小结 课件(共47张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 00:00:00 | ||
图片预览










文档简介
(共47张PPT)
九上数学同步优质课件
人教版九年级上册
一元二次方程章节复习
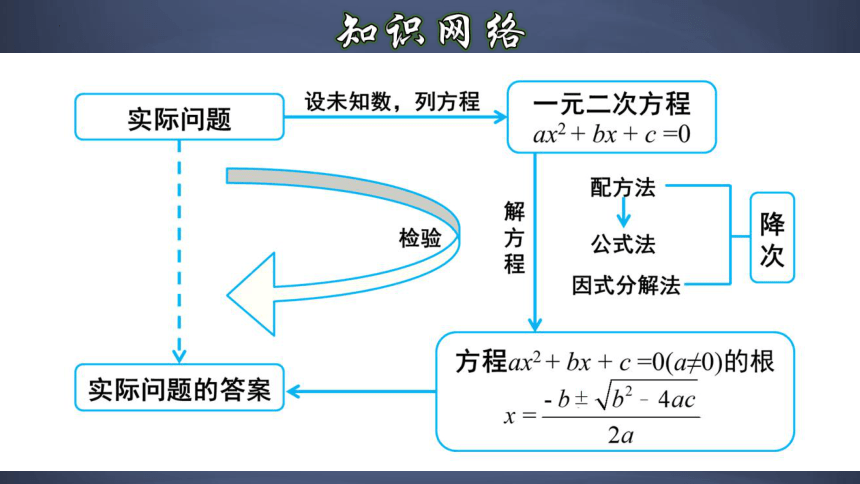
1.梳理本章的知识结构网络,回顾与复习本章知识.
2.能选择适当的方法,快速、准确地解一元二次方程,知道一元二次方程根的判别式和一元二次方程根与系数的关系,并能利用它们解决有关问题.
3.列一元二次方程解决实际问题.(重、难点)
4.进一步加深对方程思想、分类思想、转化思想(即降次)的理解与运用.
一、一元二次方程的基本概念
1.定义:只含有一个未知数的整式方程,并且都可以化为ax2+bx+c=0(a,b,c为常数,a≠0)的形式,这样的方程叫做一元二次方程.
2.一般形式:ax2+bx+c=0(a,b,c为常数,a≠0)
3.项数和系数:
二次项:ax2 二次项系数:a
一次项:bx 一次项系数:b
常数项:c
一、一元二次方程的基本概念
4.注意事项:
(1)含有一个未知数;
(2)未知数的最高次数为2;
(3)二次项系数不为0;
(4)整式方程.
5.使一元二次方程等号两边相等的未知数的值叫作一元二次方程的解(又叫做根).
二、解一元二次方程的方法
一元二次方程的解法 适用的方程类型
直接开平方法
配方法
公式法
因式分解
十字相乘法
x2+px+q=0 (二次项系数为1,p为偶数)
(x+m)2=n(n ≥ 0)
ax2 + bx +c = 0(a≠0 , b2 - 4ac≥0)
(x-m)(x-n)=0
各种一元二次方程的解法及使用类型
x2-(p+q)x+pq=0
三、一元二次方程根的判别式
一般地,式子b2-4ac叫做一元二次方程ax2+bx+c=0根的判别式,通常用希腊字母“Δ”表示它,即Δ=b2-4ac.
当Δ>0时,方程ax2+bx+c=0(a≠0)有两个不等的实数根;
当Δ=0时,方程ax2+bx+c=0(a≠0)有两个相等的实数根;
当Δ<0时,方程ax2+bx+c=0(a≠0)无实数根.
Δ>0 方程有两个不等的实数根;
Δ=0 方程有两个相等的实数根;
Δ<0 方程无实数根.
四、一元二次方程的根与系数的关系
已知x1,x2是一元二次方程ax2+bx+c=0(a,b,c为常数,a≠0)的两根. 则有:
(1)不是一般式的,要化成一般式;
(2)在方程有实数根的条件下应用,即b2-4ac≥0;
(3)在使用 时,注意“-”不要漏写.
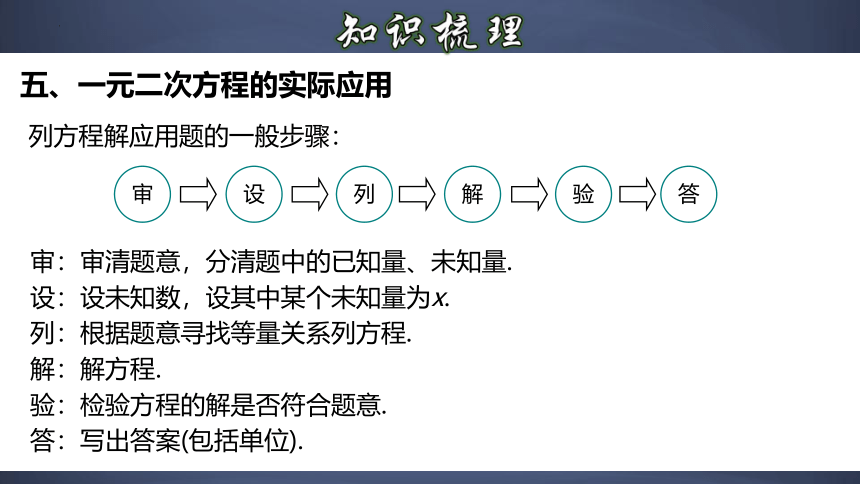
五、一元二次方程的实际应用
列方程解应用题的一般步骤:
审
设
列
解
验
答
审:审清题意,分清题中的已知量、未知量.
设:设未知数,设其中某个未知量为x.
列:根据题意寻找等量关系列方程.
解:解方程.
验:检验方程的解是否符合题意.
答:写出答案(包括单位).
几种常见类型
传播问题
握手类型问题
平均变化率问题
销售利润问题
数字问题
图形面积问题
一元二次方程的有关概念
1
例1.方程 是关于x的一元二次方程,则m的值为( )
A.3 B.-3 C.±3 D.不存在
B
【分析】根据一元二次方程的概念可知:
解得
【1-2】若关于x的方程(m-1)x2+mx-1=0是一元二次方程,则m的取值范围是( )
A.m≠1 B.m=1 C.m≥1 D.m≠0
A
【1-1】方程5x2-x-3=x2-3+x的二次项系数是___,一次项系数是____,常数项是____.
【1-3】当k_____时,关于x的方程 是一元二次方程.
4
-2
0
=-3
一元二次方程的根的应用
2
【分析】根据一元二次方程根的定义可知将x=0代入原方程一定会使方程左右两边相等,故只要把x=0代入就可以得到以m为未知数的方程m2-1=0,解得m=±1的值.这里应填-1.这种题的解题方法我们称之为“有根必代”.
例2.若关于x的一元二次方程(m-1)x2+x+m2-1=0有一个根为0,则m= .
-1
【点睛】求出m值有两个1和-1,由于原方程是一元二次方程,所以1不符合,应引起注意.
例3.已知m是一元二次方程x2-3x+2=0的一个根,则代数式2m2-6m+2022的值为( )
A.2018 B.2020 C.2022 D.2024
【分析】
∵m是一元二次方程x2-3x+2=0的一个根,
∴把x=m代入方程,得m2-3m+2=0,即:m2-3m=-2,
∴2m2-6m+2022=2(m2-3m)+2022=2×(-2)+2022=2018.
【点睛】求代数式的值,先把已知解代入,再注意观察,有时需运用到整体思想,求解时,将所求代数式的一部分看作一个整体,再用整体思想代入求值.
A
【2-1】已知2+是关于x的一元二次方程x2-4x+m=0的一个实数根,则实数m的值是( )
A.0 B.1 C.—3 D.-1
B
【2-2】若x=-2是方程ax2+bx+3=0(a≠0)的一个解,则代数式1-8a+4b的值是______.
【2-3】若x=a是方程x2-x-1=0的一个根,则-a3+2a+2020的值为_________.
2019
7
一元二次方程的解法
3
例4.三角形两边长分别为3和6,第三边的长是方程x2-13x+36=0的根,则该三角形的周长为( )
A.13 B.15 C.18 D.13或18
A
【分析】先求出方程x2﹣13x+36=0的两根,再根据三角形的三边关系,得到符合题意的边长,进而求得三角形周长.
【3-1】用配方法解方程x2-2x-5=0时,原方程应变为( )
A.(x-1)2=6 B.(x+2)2=9 C.(x+1)2=6 D.(x-2)2=9
A
【3-2】菱形ABCD的一条对角线长为6,边AB的长是一元二次方程x2-7x+12=0的一个根,则菱形ABCD的周长为( )
A.12 B.16 C.16或12 D.24
B
【3-3】用适当的方法解方程:
解:
3x-1=±2
∴x1=1,x2=-
解:x2+2x=48
(x+1)2=49
∴x1= -8,x2=
x+1=±
x2+2x+12=48+12
解:a=2,b=-7,c=5
即 t1=,t2=1.
Δ=b2-4ac
=(-7)2-4×2×5=9>0
解:3(x-2)2=x2-4
∴x1=2,x2=4
(x-2)(3x-6-x-2)=0
3(x-2)2=(x+2)(x-2)
3(x-2)2-(x+2)(x-2)=0
(x-2)(2x-8)=0
【3-3】用适当的方法解方程:
配方法的典型应用
4
例5.不论x,y为什么数,代数式4x2+3y2+8x-12y+7的值( )
A.总大于7 B.总不小于9 C.总不小于-9 D.为任意有理数
C
解:4x2+3y2+8x-12y+7
=4x2+8x+4+3y2-12y+3
=4(x2+2x+1)+3(y2 4y+1)
=4(x+1)2+3(y2 4y+4 4+1)
=4(x+1)2+3(y 2)2 9,
∵(x+1)2≥0,(y 2)2≥0,
∴4x2+3y2+8x-12y+7≥ 9.
即不论x、y为什么实数,代数式4x2+3y2+8x-12y+7的值总不小于 9.
【点睛】将二次多项式配成m(x+n)2+p的形式:①当m<0时,它有最大值p; ②当m>0时,它有最小值p.
【点睛】将二次多项式配成m(x+n)2+p的形式:①当m<0且p<0时,式子的值恒为负;②当m>0且p>0时,式子的值恒为正.
例6.试用配方的方法说明:代数式 的值恒为正数.
解:
∵无论x取何值,总有 ,
∴ .
即代数式 的值恒为正数.
例7.已知 ,求 的值.
解:∵ .
∴ ,
∴ ,
∴ ,
∴ ,
∴ .
【4-2】已知关于x的多项式 的最大值为5,则m的值可能为( )
A.1 B.2 C.3 D.4
B
【4-1】多项式x 2 ﹣6x+4y 2 +4y+20的最小值是( )
A.20 B.17 C.10 D.0
C
【4-3】已知a,b是实数,M=10a2+b2-7a+8,N=a2+b2+5a+1,试比较M ,N的值的大小.
解:∵M-N=10a2+b2-7a+8-(a2+b2+5a+1)=9a2-12a+7=(3a-2)2+3,
∵ (3a-2)2≥0,
∴(3a-2)2+3>0,
∴M>N.
一元二次方程的根的判别式的应用
5
例8.若关于x的一元二次方程 有实数根,则k的取值范
围是( )
A. B. 且 C. 且 D.
B
【分析】解:∵一元二次方程 有实数根,
∴ ,
解得 且 .
【点睛】一元二次方程有实根,说明方程可能有两个不等实根或两个相等实根两种情况.
例9.已知关于x的一元二次方程 .
(1)求证:无论k取何值,该方程总有实数根;
(2)已知等腰三角形的一边a为2,另两边恰好是这个方程的两个根,求k的值.
(1)证明:∵ 中a=1,b=-k,c=k-1
∴
∵
∴
∴无论k取何值,该方程总有实数根.
(2)若2为等腰三角形的腰,则另一边也为2,即2为方程的一个根
将x=2代入 有
4-2k+k-1=0
解得k=3
则方程为
解得x1=2,x2=1
等腰三角形三边长为2,2,1,符合三角形三边关系.
例9.已知关于x的一元二次方程 .
(1)求证:无论k取何值,该方程总有实数根;
(2)已知等腰三角形的一边a为2,另两边恰好是这个方程的两个根,求k的值.
若2为等腰三角形的底,则两根为腰且相等,有
即
解得k=2
则方程为
解得x1=x2=1
等腰三角形三边长为2,1,1,
1+1=2,不符合三角形三边关系,故k=2舍去.综上所述k的值为3.
例9.已知关于x的一元二次方程 .
(1)求证:无论k取何值,该方程总有实数根;
(2)已知等腰三角形的一边a为2,另两边恰好是这个方程的两个根,求k的值.
【5-1】已知一元二次方程 有实根,a的取值范围是( )
A. B. 且 C. D. 且
B
【分析】∵一元二次方程ax2-x+2=0有实数根,
∴ ,且a≠0,
解得 且a≠0.
【5-2】已知关于x一元二次方程 .求证:方程总有两个
不相等的实数根.
证明:由 可知a=1,b=k+2,c=k=2,
∴
∵k2≥0
∴k2+12>0
∴
∴方程总有两个不相等的实数根.
【5-3】已知关于x的方程x2-(m+1)x+2(m-1)=0.
(1)求证:无论m取何值,这个方程总有实数根;
(2)若等腰△ABC的一边长为6,另两边的长恰好是这个方程的两
个根,求△ABC的周长.
解:(1) ,
判别式 ,
所以,无论m取何值,这个方程总有实数根;
(2)将x=6代入方程,得 ,解得m=7,
即方程为x2-8x+12=0,解得x1=2,x2=6 ,
当2为等腰△ABC的腰时,底边长为6,2+2=4<6,不满足三角形四边关系,舍去,
当6为等腰△ABC的腰时,底边长为,2+6=8>6,符合三角形三边关系,此时周长为6+6+4=16.
一元二次方程的根与系数的关系
6
例10.已知方程5x2+kx-6=0的一个根是2,求它的另一个根及k的值.
解:设方程的两个根分别是x1、x2,其中x1=2.
所以:x1 x2=2x2=
即:x2=
由于x1+x2=2+ =
得:k=-7.
答:方程的另一个根是 ,k=-7.
例11.设x1,x2是方程x2-2(k-1)x+k2 =0 的两个实数根,且x12+x22 =4,求k的值.
解:由方程有两个实数根,得Δ=4(k-1)2-4k2 ≥ 0
即-8k+4≥ 0.
由根与系数的关系得 x1+x2=2(k-1), x1x2=k2.
∴x12+x22=(x1+x2)2-2x1x2
=4(k-1)2-2k2=2k2-8k+4.
由x12+x22=4,得2k2-8k+4=4,
解得 k1=0 , k2=4 .
经检验,k2 =4 不合题意,舍去.
【6-1】已知x1,x2 是一元二次方程 的两根,则
______.
4048
【6-2】已知方程3x2-18x+m=0的一个根是1,求它的另一个根及m的值.
解:设方程的两个根分别是x1、x2,其中x1=1.
所以:x1+x2=1+x2=6,
即:x2=5.
由于x1 x2=1×5=
得:m=15.
答:方程的另一个根是5,m=15.
【6-3】己知,方程x2=1-2x的两根为x1、x2,不解方程求下列各式的值: (1)x12x2+x1x22; (2),(3) (x1-x2)2.
解:将方程x2=1-2x,化为x2+4x-2=0,
∴x1+x2=-4, x1x2=- 2
x12x2+x1x22 =x1x2(x1+x2)=-2×(-4)=8
(2)
(3)(x1-x2)2=(x1+x2)2-4x1x2=(-4)2-4×(-2)=24
一元二次方程的实际应用
7
例12.2020年3月,新冠肺炎疫情在中国已经得到有效控制,但在全球却开始持续蔓延,这是对人类的考验,将对全球造成巨大影响.新冠肺炎具有人传人的特性,若一人携带病毒,未进行有效隔离,经过两轮传染后共有256人患新冠肺炎,求每轮传染中平均每个人传染了几个人?
解:设每轮传染中平均每个人传染了x个人,
根据题意,得:(x+1)2=256,
直接开平方得x+1=±16,
解得x1=15,x2=-17,
经检验都是原方程的根,但x2=-17<0不符合实际(舍去),
答:每轮传染中平均每个人传染了15个人.
例13.某药品经两次降价,零售价降为原来的一半.已知两次降价的百分率一样,求每次降价的百分率.(精确到0.1%)
解:设原价为1个单位,每次降价的百分率为 x.
根据题意,得
解这个方程,得
答:每次降价的百分率为29.3%.
例14.2019女排世界杯于9月14月至29日在日本举行,赛制为单循环比赛(即每两个队之间比赛一场)一共比赛66场,中国女排以全胜成绩卫冕世界杯冠军为国庆70周年献上大礼,则中国队在本届世界杯比赛中连胜多少场比赛?
【分析】设中国队在本届世界杯比赛中连胜
____场,则共有_______支队伍参加比赛.
( x+1 )
x
解:设中国队在本届世界杯比赛中连胜x场,列方程得:
解得:
(舍去)
答:连胜11场比赛.
例15.如图,有一张长6cm、宽5cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,用剩余(阴影)部分可制成底面积为6cm2的有盖长方体铁盒.求剪去的正方形的边长.
解:设剪去的正方形的边长为xcm,则底面的长为(5-2x)cm,宽为-x=(3-x)cm,
依题意得:(5-2x)(3-x)=6,
整理得:2x2-11x+9=0,
解得:x1=1,x2=,
当x=1时,5-2x=3,3-x=2,符合题意;
当x=时,5-2x=-4<0,不合题意,舍去.
答:剪去的正方形的边长为1cm.
例16.某蔬菜店以每千克2元的价格购进某种绿色蔬菜若干千克,然后以每千克4元的价格出售,每天可售出100千克.通过调查发现,这种蔬菜每千克的售价每降低0.1元,每天可多售出20千克,为保证每天至少售出260千克,蔬菜店决定降价销售.若将这种蔬菜每千克售价降低x元.
(1)每天的销售量是_________千克(用含x的代数式表示);
(2)销售这种蔬菜要想每天盈利300元,每千克的售价需降低多少元?
解:根据题意,得
解得
∵要保证每天至少售出260千克,即 ,得 .
∴x=1.答:每千克的售价降低1元.
200x+100
【7-1】已知3人患流感,经过两轮传染后,患流感总人数为108人,则平均每人每轮感染_____个人.
5
【7-2】距考试还有20天的时间,为鼓舞干劲,老师要求班上每一名同学要给同组的其他同学写一份拼搏进取的留言,小明所在的小组共写了30份留言,该小组共有( )
A.7人 B.6人 C.5人 D.4人
B
【7-3】截至2022年3月31日,电影《长津湖之水门桥》票房已突破37亿元.第一天票房约6亿元,三天后票房累计总收入达24亿元,如果第二天,第三天票房收入按相同的增长率增长,增长率设为x.则可列方程为( )
A. B.
C. D.
D
【7-4】某超市销售一种饮料,每瓶进价为6元.当每瓶售价为10元时,日均销售量为160瓶,经市场调查表明,每瓶售价每增加1元,日均销售量减少20瓶.若超市计划该饮料日均总利润为700元,且尽快减少库存,则每瓶该饮料售价为( )
A.11 B.12 C.13 D.14
A
【7-5】如图,矩形ABCD是景区内一块油菜花地,AB=6m,BC=8m,点E、F、G、H分别在矩形的四条边上,且AE=FC=CG=HA,现在其中修建一条观花道(阴影所示)供游人赏花.若观花道的面积为13m2,求AE的长.
解:设AE=xm,则BE=DG=(6-x)m,BF=DH=(8-x)m,
根据题意,得6×8-2×(6-x)(8-x)=13,
整理得:x2-14x+13=0,
解得:x1=1,x2=13.
∵6-x>0,∴x<6,∴x=1.
答:AE的长为1m.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步优质课件
人教版九年级上册
一元二次方程章节复习
1.梳理本章的知识结构网络,回顾与复习本章知识.
2.能选择适当的方法,快速、准确地解一元二次方程,知道一元二次方程根的判别式和一元二次方程根与系数的关系,并能利用它们解决有关问题.
3.列一元二次方程解决实际问题.(重、难点)
4.进一步加深对方程思想、分类思想、转化思想(即降次)的理解与运用.
一、一元二次方程的基本概念
1.定义:只含有一个未知数的整式方程,并且都可以化为ax2+bx+c=0(a,b,c为常数,a≠0)的形式,这样的方程叫做一元二次方程.
2.一般形式:ax2+bx+c=0(a,b,c为常数,a≠0)
3.项数和系数:
二次项:ax2 二次项系数:a
一次项:bx 一次项系数:b
常数项:c
一、一元二次方程的基本概念
4.注意事项:
(1)含有一个未知数;
(2)未知数的最高次数为2;
(3)二次项系数不为0;
(4)整式方程.
5.使一元二次方程等号两边相等的未知数的值叫作一元二次方程的解(又叫做根).
二、解一元二次方程的方法
一元二次方程的解法 适用的方程类型
直接开平方法
配方法
公式法
因式分解
十字相乘法
x2+px+q=0 (二次项系数为1,p为偶数)
(x+m)2=n(n ≥ 0)
ax2 + bx +c = 0(a≠0 , b2 - 4ac≥0)
(x-m)(x-n)=0
各种一元二次方程的解法及使用类型
x2-(p+q)x+pq=0
三、一元二次方程根的判别式
一般地,式子b2-4ac叫做一元二次方程ax2+bx+c=0根的判别式,通常用希腊字母“Δ”表示它,即Δ=b2-4ac.
当Δ>0时,方程ax2+bx+c=0(a≠0)有两个不等的实数根;
当Δ=0时,方程ax2+bx+c=0(a≠0)有两个相等的实数根;
当Δ<0时,方程ax2+bx+c=0(a≠0)无实数根.
Δ>0 方程有两个不等的实数根;
Δ=0 方程有两个相等的实数根;
Δ<0 方程无实数根.
四、一元二次方程的根与系数的关系
已知x1,x2是一元二次方程ax2+bx+c=0(a,b,c为常数,a≠0)的两根. 则有:
(1)不是一般式的,要化成一般式;
(2)在方程有实数根的条件下应用,即b2-4ac≥0;
(3)在使用 时,注意“-”不要漏写.
五、一元二次方程的实际应用
列方程解应用题的一般步骤:
审
设
列
解
验
答
审:审清题意,分清题中的已知量、未知量.
设:设未知数,设其中某个未知量为x.
列:根据题意寻找等量关系列方程.
解:解方程.
验:检验方程的解是否符合题意.
答:写出答案(包括单位).
几种常见类型
传播问题
握手类型问题
平均变化率问题
销售利润问题
数字问题
图形面积问题
一元二次方程的有关概念
1
例1.方程 是关于x的一元二次方程,则m的值为( )
A.3 B.-3 C.±3 D.不存在
B
【分析】根据一元二次方程的概念可知:
解得
【1-2】若关于x的方程(m-1)x2+mx-1=0是一元二次方程,则m的取值范围是( )
A.m≠1 B.m=1 C.m≥1 D.m≠0
A
【1-1】方程5x2-x-3=x2-3+x的二次项系数是___,一次项系数是____,常数项是____.
【1-3】当k_____时,关于x的方程 是一元二次方程.
4
-2
0
=-3
一元二次方程的根的应用
2
【分析】根据一元二次方程根的定义可知将x=0代入原方程一定会使方程左右两边相等,故只要把x=0代入就可以得到以m为未知数的方程m2-1=0,解得m=±1的值.这里应填-1.这种题的解题方法我们称之为“有根必代”.
例2.若关于x的一元二次方程(m-1)x2+x+m2-1=0有一个根为0,则m= .
-1
【点睛】求出m值有两个1和-1,由于原方程是一元二次方程,所以1不符合,应引起注意.
例3.已知m是一元二次方程x2-3x+2=0的一个根,则代数式2m2-6m+2022的值为( )
A.2018 B.2020 C.2022 D.2024
【分析】
∵m是一元二次方程x2-3x+2=0的一个根,
∴把x=m代入方程,得m2-3m+2=0,即:m2-3m=-2,
∴2m2-6m+2022=2(m2-3m)+2022=2×(-2)+2022=2018.
【点睛】求代数式的值,先把已知解代入,再注意观察,有时需运用到整体思想,求解时,将所求代数式的一部分看作一个整体,再用整体思想代入求值.
A
【2-1】已知2+是关于x的一元二次方程x2-4x+m=0的一个实数根,则实数m的值是( )
A.0 B.1 C.—3 D.-1
B
【2-2】若x=-2是方程ax2+bx+3=0(a≠0)的一个解,则代数式1-8a+4b的值是______.
【2-3】若x=a是方程x2-x-1=0的一个根,则-a3+2a+2020的值为_________.
2019
7
一元二次方程的解法
3
例4.三角形两边长分别为3和6,第三边的长是方程x2-13x+36=0的根,则该三角形的周长为( )
A.13 B.15 C.18 D.13或18
A
【分析】先求出方程x2﹣13x+36=0的两根,再根据三角形的三边关系,得到符合题意的边长,进而求得三角形周长.
【3-1】用配方法解方程x2-2x-5=0时,原方程应变为( )
A.(x-1)2=6 B.(x+2)2=9 C.(x+1)2=6 D.(x-2)2=9
A
【3-2】菱形ABCD的一条对角线长为6,边AB的长是一元二次方程x2-7x+12=0的一个根,则菱形ABCD的周长为( )
A.12 B.16 C.16或12 D.24
B
【3-3】用适当的方法解方程:
解:
3x-1=±2
∴x1=1,x2=-
解:x2+2x=48
(x+1)2=49
∴x1= -8,x2=
x+1=±
x2+2x+12=48+12
解:a=2,b=-7,c=5
即 t1=,t2=1.
Δ=b2-4ac
=(-7)2-4×2×5=9>0
解:3(x-2)2=x2-4
∴x1=2,x2=4
(x-2)(3x-6-x-2)=0
3(x-2)2=(x+2)(x-2)
3(x-2)2-(x+2)(x-2)=0
(x-2)(2x-8)=0
【3-3】用适当的方法解方程:
配方法的典型应用
4
例5.不论x,y为什么数,代数式4x2+3y2+8x-12y+7的值( )
A.总大于7 B.总不小于9 C.总不小于-9 D.为任意有理数
C
解:4x2+3y2+8x-12y+7
=4x2+8x+4+3y2-12y+3
=4(x2+2x+1)+3(y2 4y+1)
=4(x+1)2+3(y2 4y+4 4+1)
=4(x+1)2+3(y 2)2 9,
∵(x+1)2≥0,(y 2)2≥0,
∴4x2+3y2+8x-12y+7≥ 9.
即不论x、y为什么实数,代数式4x2+3y2+8x-12y+7的值总不小于 9.
【点睛】将二次多项式配成m(x+n)2+p的形式:①当m<0时,它有最大值p; ②当m>0时,它有最小值p.
【点睛】将二次多项式配成m(x+n)2+p的形式:①当m<0且p<0时,式子的值恒为负;②当m>0且p>0时,式子的值恒为正.
例6.试用配方的方法说明:代数式 的值恒为正数.
解:
∵无论x取何值,总有 ,
∴ .
即代数式 的值恒为正数.
例7.已知 ,求 的值.
解:∵ .
∴ ,
∴ ,
∴ ,
∴ ,
∴ .
【4-2】已知关于x的多项式 的最大值为5,则m的值可能为( )
A.1 B.2 C.3 D.4
B
【4-1】多项式x 2 ﹣6x+4y 2 +4y+20的最小值是( )
A.20 B.17 C.10 D.0
C
【4-3】已知a,b是实数,M=10a2+b2-7a+8,N=a2+b2+5a+1,试比较M ,N的值的大小.
解:∵M-N=10a2+b2-7a+8-(a2+b2+5a+1)=9a2-12a+7=(3a-2)2+3,
∵ (3a-2)2≥0,
∴(3a-2)2+3>0,
∴M>N.
一元二次方程的根的判别式的应用
5
例8.若关于x的一元二次方程 有实数根,则k的取值范
围是( )
A. B. 且 C. 且 D.
B
【分析】解:∵一元二次方程 有实数根,
∴ ,
解得 且 .
【点睛】一元二次方程有实根,说明方程可能有两个不等实根或两个相等实根两种情况.
例9.已知关于x的一元二次方程 .
(1)求证:无论k取何值,该方程总有实数根;
(2)已知等腰三角形的一边a为2,另两边恰好是这个方程的两个根,求k的值.
(1)证明:∵ 中a=1,b=-k,c=k-1
∴
∵
∴
∴无论k取何值,该方程总有实数根.
(2)若2为等腰三角形的腰,则另一边也为2,即2为方程的一个根
将x=2代入 有
4-2k+k-1=0
解得k=3
则方程为
解得x1=2,x2=1
等腰三角形三边长为2,2,1,符合三角形三边关系.
例9.已知关于x的一元二次方程 .
(1)求证:无论k取何值,该方程总有实数根;
(2)已知等腰三角形的一边a为2,另两边恰好是这个方程的两个根,求k的值.
若2为等腰三角形的底,则两根为腰且相等,有
即
解得k=2
则方程为
解得x1=x2=1
等腰三角形三边长为2,1,1,
1+1=2,不符合三角形三边关系,故k=2舍去.综上所述k的值为3.
例9.已知关于x的一元二次方程 .
(1)求证:无论k取何值,该方程总有实数根;
(2)已知等腰三角形的一边a为2,另两边恰好是这个方程的两个根,求k的值.
【5-1】已知一元二次方程 有实根,a的取值范围是( )
A. B. 且 C. D. 且
B
【分析】∵一元二次方程ax2-x+2=0有实数根,
∴ ,且a≠0,
解得 且a≠0.
【5-2】已知关于x一元二次方程 .求证:方程总有两个
不相等的实数根.
证明:由 可知a=1,b=k+2,c=k=2,
∴
∵k2≥0
∴k2+12>0
∴
∴方程总有两个不相等的实数根.
【5-3】已知关于x的方程x2-(m+1)x+2(m-1)=0.
(1)求证:无论m取何值,这个方程总有实数根;
(2)若等腰△ABC的一边长为6,另两边的长恰好是这个方程的两
个根,求△ABC的周长.
解:(1) ,
判别式 ,
所以,无论m取何值,这个方程总有实数根;
(2)将x=6代入方程,得 ,解得m=7,
即方程为x2-8x+12=0,解得x1=2,x2=6 ,
当2为等腰△ABC的腰时,底边长为6,2+2=4<6,不满足三角形四边关系,舍去,
当6为等腰△ABC的腰时,底边长为,2+6=8>6,符合三角形三边关系,此时周长为6+6+4=16.
一元二次方程的根与系数的关系
6
例10.已知方程5x2+kx-6=0的一个根是2,求它的另一个根及k的值.
解:设方程的两个根分别是x1、x2,其中x1=2.
所以:x1 x2=2x2=
即:x2=
由于x1+x2=2+ =
得:k=-7.
答:方程的另一个根是 ,k=-7.
例11.设x1,x2是方程x2-2(k-1)x+k2 =0 的两个实数根,且x12+x22 =4,求k的值.
解:由方程有两个实数根,得Δ=4(k-1)2-4k2 ≥ 0
即-8k+4≥ 0.
由根与系数的关系得 x1+x2=2(k-1), x1x2=k2.
∴x12+x22=(x1+x2)2-2x1x2
=4(k-1)2-2k2=2k2-8k+4.
由x12+x22=4,得2k2-8k+4=4,
解得 k1=0 , k2=4 .
经检验,k2 =4 不合题意,舍去.
【6-1】已知x1,x2 是一元二次方程 的两根,则
______.
4048
【6-2】已知方程3x2-18x+m=0的一个根是1,求它的另一个根及m的值.
解:设方程的两个根分别是x1、x2,其中x1=1.
所以:x1+x2=1+x2=6,
即:x2=5.
由于x1 x2=1×5=
得:m=15.
答:方程的另一个根是5,m=15.
【6-3】己知,方程x2=1-2x的两根为x1、x2,不解方程求下列各式的值: (1)x12x2+x1x22; (2),(3) (x1-x2)2.
解:将方程x2=1-2x,化为x2+4x-2=0,
∴x1+x2=-4, x1x2=- 2
x12x2+x1x22 =x1x2(x1+x2)=-2×(-4)=8
(2)
(3)(x1-x2)2=(x1+x2)2-4x1x2=(-4)2-4×(-2)=24
一元二次方程的实际应用
7
例12.2020年3月,新冠肺炎疫情在中国已经得到有效控制,但在全球却开始持续蔓延,这是对人类的考验,将对全球造成巨大影响.新冠肺炎具有人传人的特性,若一人携带病毒,未进行有效隔离,经过两轮传染后共有256人患新冠肺炎,求每轮传染中平均每个人传染了几个人?
解:设每轮传染中平均每个人传染了x个人,
根据题意,得:(x+1)2=256,
直接开平方得x+1=±16,
解得x1=15,x2=-17,
经检验都是原方程的根,但x2=-17<0不符合实际(舍去),
答:每轮传染中平均每个人传染了15个人.
例13.某药品经两次降价,零售价降为原来的一半.已知两次降价的百分率一样,求每次降价的百分率.(精确到0.1%)
解:设原价为1个单位,每次降价的百分率为 x.
根据题意,得
解这个方程,得
答:每次降价的百分率为29.3%.
例14.2019女排世界杯于9月14月至29日在日本举行,赛制为单循环比赛(即每两个队之间比赛一场)一共比赛66场,中国女排以全胜成绩卫冕世界杯冠军为国庆70周年献上大礼,则中国队在本届世界杯比赛中连胜多少场比赛?
【分析】设中国队在本届世界杯比赛中连胜
____场,则共有_______支队伍参加比赛.
( x+1 )
x
解:设中国队在本届世界杯比赛中连胜x场,列方程得:
解得:
(舍去)
答:连胜11场比赛.
例15.如图,有一张长6cm、宽5cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,用剩余(阴影)部分可制成底面积为6cm2的有盖长方体铁盒.求剪去的正方形的边长.
解:设剪去的正方形的边长为xcm,则底面的长为(5-2x)cm,宽为-x=(3-x)cm,
依题意得:(5-2x)(3-x)=6,
整理得:2x2-11x+9=0,
解得:x1=1,x2=,
当x=1时,5-2x=3,3-x=2,符合题意;
当x=时,5-2x=-4<0,不合题意,舍去.
答:剪去的正方形的边长为1cm.
例16.某蔬菜店以每千克2元的价格购进某种绿色蔬菜若干千克,然后以每千克4元的价格出售,每天可售出100千克.通过调查发现,这种蔬菜每千克的售价每降低0.1元,每天可多售出20千克,为保证每天至少售出260千克,蔬菜店决定降价销售.若将这种蔬菜每千克售价降低x元.
(1)每天的销售量是_________千克(用含x的代数式表示);
(2)销售这种蔬菜要想每天盈利300元,每千克的售价需降低多少元?
解:根据题意,得
解得
∵要保证每天至少售出260千克,即 ,得 .
∴x=1.答:每千克的售价降低1元.
200x+100
【7-1】已知3人患流感,经过两轮传染后,患流感总人数为108人,则平均每人每轮感染_____个人.
5
【7-2】距考试还有20天的时间,为鼓舞干劲,老师要求班上每一名同学要给同组的其他同学写一份拼搏进取的留言,小明所在的小组共写了30份留言,该小组共有( )
A.7人 B.6人 C.5人 D.4人
B
【7-3】截至2022年3月31日,电影《长津湖之水门桥》票房已突破37亿元.第一天票房约6亿元,三天后票房累计总收入达24亿元,如果第二天,第三天票房收入按相同的增长率增长,增长率设为x.则可列方程为( )
A. B.
C. D.
D
【7-4】某超市销售一种饮料,每瓶进价为6元.当每瓶售价为10元时,日均销售量为160瓶,经市场调查表明,每瓶售价每增加1元,日均销售量减少20瓶.若超市计划该饮料日均总利润为700元,且尽快减少库存,则每瓶该饮料售价为( )
A.11 B.12 C.13 D.14
A
【7-5】如图,矩形ABCD是景区内一块油菜花地,AB=6m,BC=8m,点E、F、G、H分别在矩形的四条边上,且AE=FC=CG=HA,现在其中修建一条观花道(阴影所示)供游人赏花.若观花道的面积为13m2,求AE的长.
解:设AE=xm,则BE=DG=(6-x)m,BF=DH=(8-x)m,
根据题意,得6×8-2×(6-x)(8-x)=13,
整理得:x2-14x+13=0,
解得:x1=1,x2=13.
∵6-x>0,∴x<6,∴x=1.
答:AE的长为1m.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
