古典概型(2)[下学期]

课件14张PPT。1.古典概型的概念2.古典概型的概率公式3.列表法和树状图§3.2 古典概型温故知新1)试验的所有可能结果(即基本事件)只有有限个,每次试验只出现其中的一个结果; 2)每一个结果出现的可能性相同。1.单选题是标准化考试中常用的题型.如果考生不会做,他从4个备选答案中随机地选择一个作答,他答对的概率是____.
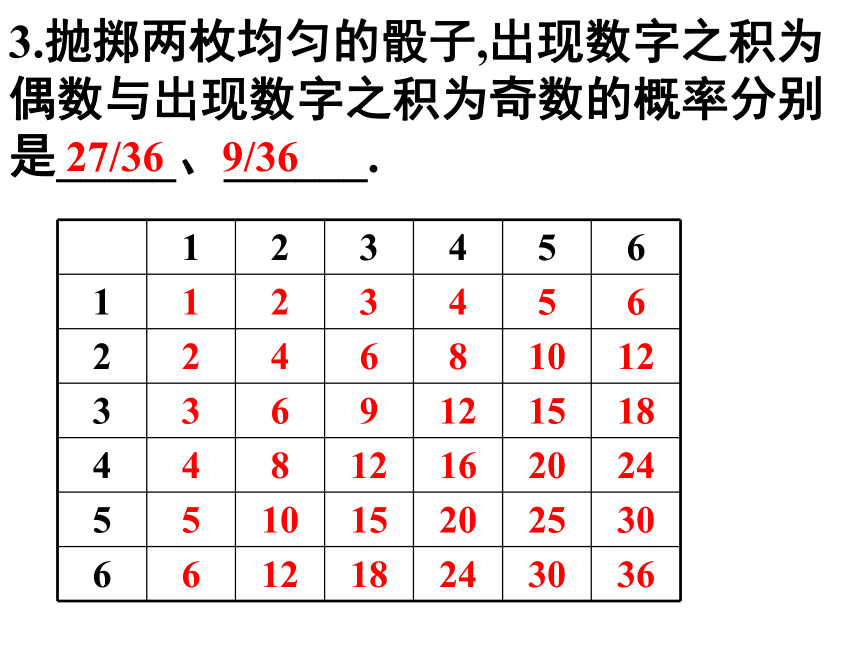
2. 从集合 {1,2,3,4,5} 的所有子集中任取一个, 这个集合恰是集合 {1,2,3} 的子集的概率是____.1/321/43.抛掷两枚均匀的骰子,出现数字之积为偶数与出现数字之积为奇数的概率分别是_____、______.
27/369/364.从一副去掉大、小王的扑克牌中任意抽取一张:
⑴是A的概率是____;
⑵是梅花的概率是____;
⑶是红色花 (J、Q、K)牌的概率是_____.4/52=1/1313/52=1/4=3/266/52一般来说,在建立概率模型时把什么看作是基本事件,即试验结果是人为规定的,也就是说,对于同一个随机试验,可以根据需要,建立满足我们要求的概率模型建立概率模型的背景掷一粒均匀的骰子,(1)若考虑向上的点数是多少,则出现1,2,3,4,5,6点的概率都是 (2)若考虑向上的点数是奇数还是偶数,则分别出现奇数或偶数的概率都是1/61/2(3)若要在掷一粒均匀骰子的试验中,欲使每一个结果出现的概率都是1/3,怎么办?把骰子的6个面分为3组(如相对两面为一组),分别涂上三种不同的颜色例.袋里装有 1 个白球和 1 个黑球,这 2 个球除了颜色外完全相同,2 个人按顺序依次从中摸出一个球.试计算第二个人摸到白球的概率。分析:1.完成一次试验是指什么？
2.总的基本事件数是多少？
符合要求的基本事件数是多少？例.袋里装有 2 个白球和 1 个黑球,这 3 个球除了颜色外完全相同,3 个人按顺序依次从中摸出一个球.试计算第二个人摸到白球的概率。树状图变1.袋里装有 2 个白球和 2 个黑球,这四个球除了颜色外完全相同, 4 个人按顺序依次从中摸出一个球.试计算第二个人摸到白球的概率。分析:1.完成一次试验是指什么？
2.总的基本事件数是多少？
符合要求的基本事件数是多少？变1.袋里装有2个白球和2个黑球,这4个球除颜色外完全相同,4人按顺序依次从中摸出一球.试计算第二个人摸到白球的概率.第一步第二步第三步第四步树状图变1.袋里装有2个白球和2个黑球,这4个球除颜色外完全相同,4人按顺序依次从中摸出一球.试计算第二个人摸到白球的概率.第一步第二步第三步1第四步树状图教材P165 法1,法2,法3评析:法(一) 利用树状图列出了试验的所有可能结果(共24种),可以计算4个人依次摸球的任何一个事件的概率;法(二) 利用试验结果的对称性,只考虑前两个人摸球的情况,所有可能结果减少为12种法(三)只考虑球的颜色,对2个白球不加区分,所有可能结果减少6种法(四)只考虑第二个人摸出的球的情况,所有可能结果变为4种,该模型最简单！变2.袋里装有 1 个白球和 3 个黑球,这4个球除颜色外完全相同, 4个人按顺序依次从中摸出一球.求第二个人摸到白球的概率。练习:建立适当的古典概型解决下列问题: (1)口袋里装有100个球,其中有1个白球和99个黑球,这些球除颜色外完全相同.100个人依次从中摸出一球,求第81个人摸到白球的概率.(2)100个人依次抓阄决定1件奖品的归属,求最后一个人中奖的概率.练习:建立适当的古典概型解决下列问题: (1)口袋里装有100个球,其中有1个白球和99个黑球,这些球除颜色外完全相同.100个人依次从中摸出一球,求第81个人摸到白球的概率.分析:我们可以只考虑第81个人摸球的情况.他可能摸到100个球中的任何一个,这100个球出现的可能性相同,且第81个人摸到白球的可能结果只有1种,因此第81个人摸到白球的概率为1/100.(2)100个人依次抓阄决定1件奖品的归属,求最后一个人中奖的概率.分析:只考虑最后一个抓阄的情况,他可能找到100个阄中的任何一个,而他抓到有奖的阄的结果只有一种,因此,最后一个人中奖的概率为1/100.探究2.甲、乙、丙、丁四位同学排队,其中甲站在排头的概率是______. 1.假设储蓄卡的密码由6个数字组成.一个完全不知道密码的人到自动取款机上能取到钱的概率是多少？练习:P168练习T2作业 (可不抄题)
书本P178习题3-2 4 5 6 7 8
课外:在学有余力的情况下,可以先做P87---P92