古典概型(3)[下学期]
图片预览



文档简介
课件9张PPT。§3.2 古典概型导入练习 一袋中装有2个红球,3个黄球,5个白球,各球除了颜色外其他都相同,从中任意摸出 一球,设A=“摸出红球”,B=“摸出黄球”,C=“摸出白球”, D=“摸出的球不是白球”.回答下列问题:(1)求这些事件发生的概率 P(A),P(B),P(C),P(D);
(2) 摸出红球或黄球的概率是多少?
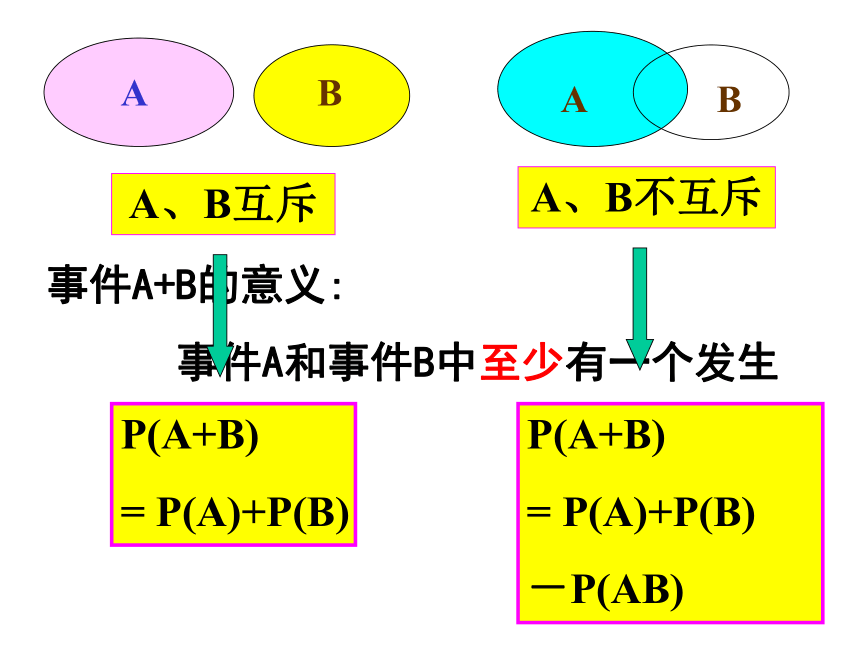
(3)C与D能同时发生吗? A与B呢?温故知新列表法树状图法列举,抽象整体思维,对称意识互斥事件在一个随机试验中,把一次试验下不能同时发生的两个(或多个)事件称为互斥事件 抛掷一枚骰子一次,下面的事件A与事件B是互斥事件吗?
1、A = “点数为 2 ”,B = “点数为 3 ”
2、A = “点数为 2 ”,B = “点数为 3 或 4 ”
3、A = “点数为 3 ”,B = “点数为 3 或 4 ”
4、A = “点数为 3 ”,B = “点数小于3 ”
5、A=“点数大于3”, B = “点数小于6 ”辨析A、B互斥A、B不互斥事件A+B的意义:
事件A和事件B中至少有一个发生P(A+B)
= P(A)+P(B)P(A+B)
= P(A)+P(B)
-P(AB)例1:从一箱产品中随机地抽取一件产品,设A= “抽到的是一等品”,B=“抽到的是二等品”,C=“抽到的是三等品”.且(A)=0.7,P(B)=0.1,P(C)=0.05 . 求下列事件的概率:
⑴事件D=“抽到的是一等品或三等品”
⑵事件E=“抽到的是二等品或三等品”阅读教材P169-171例3~例5小结 解题步骤:⑴判断事件间的容斥关系;⑵运用公式.P(A+B)=P(A)+P(B)-P(AB)当A、B互斥时, P(AB)=0ABA+B=UB、U是互斥事件吗?试验:将一枚质地均匀的骰子随机抛掷一次,观察骰子向上一面的点数.设 U = “出现点数的全体”, A=“出现的点数是偶数” B=“出现的点数是奇数”,A、B 是互斥事件吗?A、U是互斥事件吗?A、B 是互斥事件A、B 是对立事件 记事件A的对立事件为:对立事件:不会同时发生且必有一个发生互斥事件与对立事件的区别与联系:
互斥事件:不同时发生,可以是多个事件,
不一定能组成全体 可能都不发生
对立事件:不同时发生,只能是两个事件,
两个事件组成事件的全体
两者必有一个发生互斥事件P(A+B) = P(A) + P(B)对立事件P(A)=1-P(B)=1-互斥未必对立对立一定互斥例2:某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛,判断下列每对事件是不是互斥事件,是不是对立事件。
⑴ “恰有1名男生” 与 “恰有2名男生”
⑵ “至少有1名男生” 与 “全是男生”
⑶ “至少有1名男生” 与 “全是女生”
⑷ “至少有1名男生” 与 “至少有1名女生”例3:某学校成立了数学、英语、艺术3个课外兴趣小组,3个小组分别有39、32、33个成员,有些同学参加了不止一个小组,具体情况如图所示。随机选取1个成员:
⑴求他至少参加了2个小组的概率;
⑵求他参加不超过2个小组的概率。练习:P173练习T1~3(口答), 4互斥事件:不同时发生的两个或多个事件
对立事件:必有一个发生的两个彼此互斥的事件互斥事件P(A+B) = P(A) + P(B)对立事件P(A)=1-P(B)=1-互斥未必对立对立一定互斥小结作业:P179 9、10、11(不抄题)
(2) 摸出红球或黄球的概率是多少?
(3)C与D能同时发生吗? A与B呢?温故知新列表法树状图法列举,抽象整体思维,对称意识互斥事件在一个随机试验中,把一次试验下不能同时发生的两个(或多个)事件称为互斥事件 抛掷一枚骰子一次,下面的事件A与事件B是互斥事件吗?
1、A = “点数为 2 ”,B = “点数为 3 ”
2、A = “点数为 2 ”,B = “点数为 3 或 4 ”
3、A = “点数为 3 ”,B = “点数为 3 或 4 ”
4、A = “点数为 3 ”,B = “点数小于3 ”
5、A=“点数大于3”, B = “点数小于6 ”辨析A、B互斥A、B不互斥事件A+B的意义:
事件A和事件B中至少有一个发生P(A+B)
= P(A)+P(B)P(A+B)
= P(A)+P(B)
-P(AB)例1:从一箱产品中随机地抽取一件产品,设A= “抽到的是一等品”,B=“抽到的是二等品”,C=“抽到的是三等品”.且(A)=0.7,P(B)=0.1,P(C)=0.05 . 求下列事件的概率:
⑴事件D=“抽到的是一等品或三等品”
⑵事件E=“抽到的是二等品或三等品”阅读教材P169-171例3~例5小结 解题步骤:⑴判断事件间的容斥关系;⑵运用公式.P(A+B)=P(A)+P(B)-P(AB)当A、B互斥时, P(AB)=0ABA+B=UB、U是互斥事件吗?试验:将一枚质地均匀的骰子随机抛掷一次,观察骰子向上一面的点数.设 U = “出现点数的全体”, A=“出现的点数是偶数” B=“出现的点数是奇数”,A、B 是互斥事件吗?A、U是互斥事件吗?A、B 是互斥事件A、B 是对立事件 记事件A的对立事件为:对立事件:不会同时发生且必有一个发生互斥事件与对立事件的区别与联系:
互斥事件:不同时发生,可以是多个事件,
不一定能组成全体 可能都不发生
对立事件:不同时发生,只能是两个事件,
两个事件组成事件的全体
两者必有一个发生互斥事件P(A+B) = P(A) + P(B)对立事件P(A)=1-P(B)=1-互斥未必对立对立一定互斥例2:某小组有3名男生和2名女生,从中任选2名同学参加演讲比赛,判断下列每对事件是不是互斥事件,是不是对立事件。
⑴ “恰有1名男生” 与 “恰有2名男生”
⑵ “至少有1名男生” 与 “全是男生”
⑶ “至少有1名男生” 与 “全是女生”
⑷ “至少有1名男生” 与 “至少有1名女生”例3:某学校成立了数学、英语、艺术3个课外兴趣小组,3个小组分别有39、32、33个成员,有些同学参加了不止一个小组,具体情况如图所示。随机选取1个成员:
⑴求他至少参加了2个小组的概率;
⑵求他参加不超过2个小组的概率。练习:P173练习T1~3(口答), 4互斥事件:不同时发生的两个或多个事件
对立事件:必有一个发生的两个彼此互斥的事件互斥事件P(A+B) = P(A) + P(B)对立事件P(A)=1-P(B)=1-互斥未必对立对立一定互斥小结作业:P179 9、10、11(不抄题)
