《平面向量》专题12 平面向量非坐标分解代换 专题讲义(Word版含答案)
文档属性
| 名称 | 《平面向量》专题12 平面向量非坐标分解代换 专题讲义(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 381.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 12:53:32 | ||
图片预览

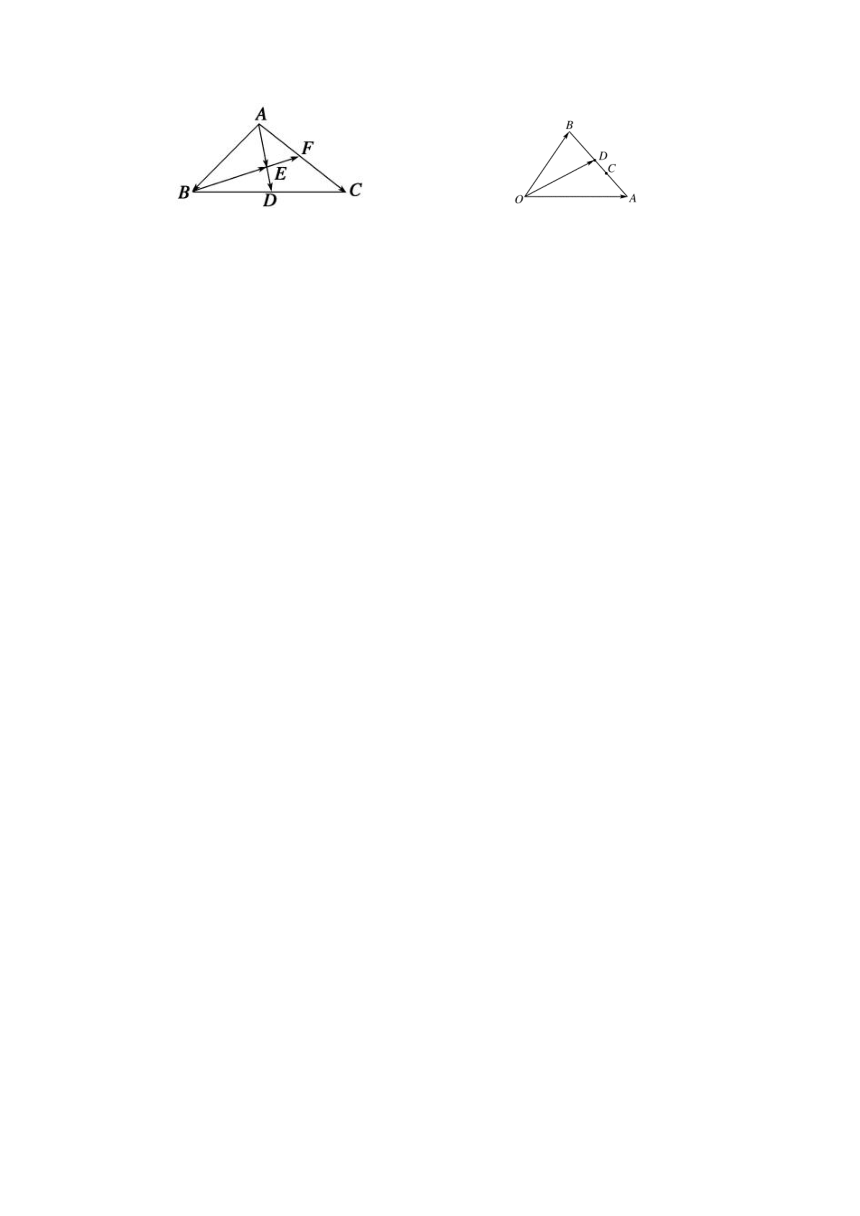


文档简介
《平面向量》专题12-1 非坐标分解代换
(5套4页,含答案)
知识点:
非坐标分解代换: 该专题题目用坐标法也是可以做的,不过为了训练学生分解向量,建议不用坐标分析。
典型例题1:
如图七所示,△ABC中,=,DE∥BC交AC于E,AM是BC边上中线,交DE于N.设=a,=b,用a,b分别表示向量,,,,,. ([endnoteRef:0])
[0: 答案:,,,,,]
如图所示,在 ABCD中,=a,=b,=3,M为BC的中点,则=__[endnoteRef:1]___.(用a、b表示).
[1: [答案] (b-a);
[解析] =++
=-++
=--+(+)
=-b-a+(a+b)
=b-a=(b-a).
]
设D为△ABC所在平面内一点,则( [endnoteRef:2] )
(A) = + (B) = (C) = + (D) = [2: 【答案】A
【解析】由题知=,故选A.
]
随堂练习1:
如图八所示,在△ABC中,D、F分别是BC、AC的中点,=,=a,=b,用a、b表示向量、、、、; ([endnoteRef:3])
[3: 答案:,,,,]
已知=a,=b,C为线段AB上距A较近的一个三等分点,D为线段CB上距C较近的一个三等分点,则用a、b表示为( [endnoteRef:4] ) A.(4a+5b) B.(9a+7b) C.(2a+b) D.(3a+b)
[4: [答案] A;
[解析] 利用向量加法和减法的几何意义和平面向量基本定理求解.
∵=+,=+
=+=+=.
而=b-a,∴=b-a,
∴=+=a+(b-a)=a+b.
]
《平面向量》专题12-2 非坐标分解代换
如图在三角形ABC中,AD=AB/3,E为CD中点,EF=EB/3,,,请用,,来表示CD,BE,DF。
在中,为边上的中线,为的中点,则([endnoteRef:5] )
A. B. C. D. [5: 答案:A
解答:
.]
如图所示,已知△ABC中,D为BC的中点,E,F为BC的三等分点,若=a,=b,用a,b表示,,.[endnoteRef:6]
[6: 答案:解 =+=+=a+(b-a)=a+b;
=+=+=a+(b-a)=a+b;
=+=+=a+(b-a)=a+b.
]
如图所示,向量、、的终点A、B、C在一条直线上,且=-3.设=p,=q,=r,
则以下等式中成立的是( [endnoteRef:7] )
A.r=-p+q B.r=-p+2q C.r=p-q D.r=-q+2p [7: [答案] A;
[解析] ∵=+,=-3=3,
∴=.
∴=+=+(-).
∴r=q+(r-p).
∴r=-p+q.
]
《平面向量》专题12-3 非坐标分解代换
如图在平行四边形ABCD中,E为BC中点,F为DE中点,FG=FA/3,,,请用,,来表示AF,DE,BG。
如图所示,D是△ABC的边AB上的中点,则向量=___[endnoteRef:8]___.(填写正确的序号)
①-+ ②-- ③- ④+
[8: 答案:①;
解析 -+=+=+=.
]
如图,在△ABC中,,若,则=( [endnoteRef:9] )
A、 B、 C、 D、
[9: 答案:D;
解析:过点分别作,,交点分别为,,由已知得,,故.故选D]
如图六,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB=OB.DC与OA交于E,设=a,=b,用a,b表示向量,.([endnoteRef:10])
[10: 答案:,]
《平面向量》专题12-4 非坐标分解代换
设D为△ABC所在平面内一点,且,则( [endnoteRef:11] )
[11: 答案:A;]
如图2,平行四边形中,是的中点,是的中点,若,,
则( [endnoteRef:12] ) A. B. C. D.
[12: 答案:A]
如图,在△OAB中,已知P为线段AB上的一点,
(1)若,求,的值;
(2)若,,,
且与的夹角为60°时,求 的值.([endnoteRef:13]) [13: 答案:解(1)∵,
∴,即,
∴,即,.
(2)∵,
∴,即,
∴,
∴,.
]
《平面向量》专题12-5 非坐标分解代换
设D为△ABC所在平面内一点,且,则( [endnoteRef:14] )
A. B. C. D. [14: 答案:A;]
,点在边上,,设,则( [endnoteRef:15])
[15: 【答案】]
如右图,等边△中,,则____[endnoteRef:16]____
[16: 答案:;
【解析】,
]
(5套4页,含答案)
知识点:
非坐标分解代换: 该专题题目用坐标法也是可以做的,不过为了训练学生分解向量,建议不用坐标分析。
典型例题1:
如图七所示,△ABC中,=,DE∥BC交AC于E,AM是BC边上中线,交DE于N.设=a,=b,用a,b分别表示向量,,,,,. ([endnoteRef:0])
[0: 答案:,,,,,]
如图所示,在 ABCD中,=a,=b,=3,M为BC的中点,则=__[endnoteRef:1]___.(用a、b表示).
[1: [答案] (b-a);
[解析] =++
=-++
=--+(+)
=-b-a+(a+b)
=b-a=(b-a).
]
设D为△ABC所在平面内一点,则( [endnoteRef:2] )
(A) = + (B) = (C) = + (D) = [2: 【答案】A
【解析】由题知=,故选A.
]
随堂练习1:
如图八所示,在△ABC中,D、F分别是BC、AC的中点,=,=a,=b,用a、b表示向量、、、、; ([endnoteRef:3])
[3: 答案:,,,,]
已知=a,=b,C为线段AB上距A较近的一个三等分点,D为线段CB上距C较近的一个三等分点,则用a、b表示为( [endnoteRef:4] ) A.(4a+5b) B.(9a+7b) C.(2a+b) D.(3a+b)
[4: [答案] A;
[解析] 利用向量加法和减法的几何意义和平面向量基本定理求解.
∵=+,=+
=+=+=.
而=b-a,∴=b-a,
∴=+=a+(b-a)=a+b.
]
《平面向量》专题12-2 非坐标分解代换
如图在三角形ABC中,AD=AB/3,E为CD中点,EF=EB/3,,,请用,,来表示CD,BE,DF。
在中,为边上的中线,为的中点,则([endnoteRef:5] )
A. B. C. D. [5: 答案:A
解答:
.]
如图所示,已知△ABC中,D为BC的中点,E,F为BC的三等分点,若=a,=b,用a,b表示,,.[endnoteRef:6]
[6: 答案:解 =+=+=a+(b-a)=a+b;
=+=+=a+(b-a)=a+b;
=+=+=a+(b-a)=a+b.
]
如图所示,向量、、的终点A、B、C在一条直线上,且=-3.设=p,=q,=r,
则以下等式中成立的是( [endnoteRef:7] )
A.r=-p+q B.r=-p+2q C.r=p-q D.r=-q+2p [7: [答案] A;
[解析] ∵=+,=-3=3,
∴=.
∴=+=+(-).
∴r=q+(r-p).
∴r=-p+q.
]
《平面向量》专题12-3 非坐标分解代换
如图在平行四边形ABCD中,E为BC中点,F为DE中点,FG=FA/3,,,请用,,来表示AF,DE,BG。
如图所示,D是△ABC的边AB上的中点,则向量=___[endnoteRef:8]___.(填写正确的序号)
①-+ ②-- ③- ④+
[8: 答案:①;
解析 -+=+=+=.
]
如图,在△ABC中,,若,则=( [endnoteRef:9] )
A、 B、 C、 D、
[9: 答案:D;
解析:过点分别作,,交点分别为,,由已知得,,故.故选D]
如图六,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB=OB.DC与OA交于E,设=a,=b,用a,b表示向量,.([endnoteRef:10])
[10: 答案:,]
《平面向量》专题12-4 非坐标分解代换
设D为△ABC所在平面内一点,且,则( [endnoteRef:11] )
[11: 答案:A;]
如图2,平行四边形中,是的中点,是的中点,若,,
则( [endnoteRef:12] ) A. B. C. D.
[12: 答案:A]
如图,在△OAB中,已知P为线段AB上的一点,
(1)若,求,的值;
(2)若,,,
且与的夹角为60°时,求 的值.([endnoteRef:13]) [13: 答案:解(1)∵,
∴,即,
∴,即,.
(2)∵,
∴,即,
∴,
∴,.
]
《平面向量》专题12-5 非坐标分解代换
设D为△ABC所在平面内一点,且,则( [endnoteRef:14] )
A. B. C. D. [14: 答案:A;]
,点在边上,,设,则( [endnoteRef:15])
[15: 【答案】]
如右图,等边△中,,则____[endnoteRef:16]____
[16: 答案:;
【解析】,
]
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
