11.1.2三角形的高、中线与角平分线 课件(共22张PPT)
文档属性
| 名称 | 11.1.2三角形的高、中线与角平分线 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 13:42:48 | ||
图片预览





文档简介
(共22张PPT)
11.1.2三角形的高、中线与角平分线
人教版 八年级上册
教学目标
教学目标:
(1)理解三角形的高、中线与角平分线的概念;
(2)会画三角形的高、中线与角平分线;
(3)三角形在实际生活中的应用.
重点:(1)了解三角形的高、中线与角平分线的概念,会用工具准确画出三角形的高、中线与角平分线。
(2)了解三角形的三条高、三条中线与三条角平分线分别交于一点。
难点:(1)三角形平分线与角平分线的区别,三角形的高与垂线的区别。
(2)三角形高的画法。
(3)不同的三角形三条高的位置关系。
新知导入
问题 还记得“过一点画已知直线的垂线”吗?
如何画线段的中点,怎样画∠ABC 的角平分线?
●
●
●
A
B
C
●
新知讲解
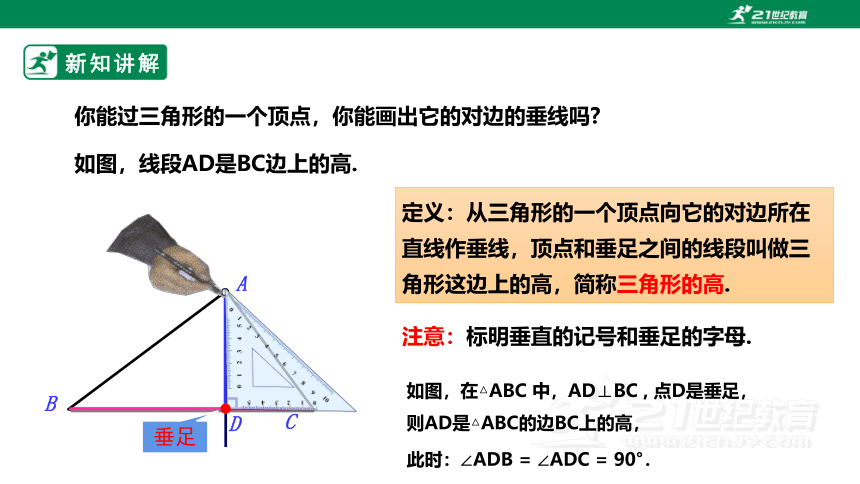
你能过三角形的一个顶点,你能画出它的对边的垂线吗
如图,线段AD是BC边上的高.
注意:标明垂直的记号和垂足的字母.
定义:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高.
A
B
C
D
垂足
如图,在△ABC 中,AD⊥BC , 点D是垂足,则AD是△ABC的边BC上的高,
此时:∠ADB = ∠ADC = 90°.
新知讲解
锐角三角形的三条高
每人画一个锐角三角形.
(1) 你能画出这个三角形的三条高吗
(2) 这三条高之间有怎样的位置关系?
O
锐角三角形的三条高是在三角形的内部还是外部
A
B
C
D
E
F
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
新知讲解
直角三角形的三条高
在纸上画出一个直角三角形.
A
B
C
(1)画出直角三角形的三条高.
直角边BC边上的高是______;
AB
直角边AB边上的高是______;
CB
(2)它们有怎样的位置关系?
D
斜边AC边上的高是_______.
BD
●
直角三角形的三条高交于直角顶点.
新知讲解
A
B
C
D
E
F
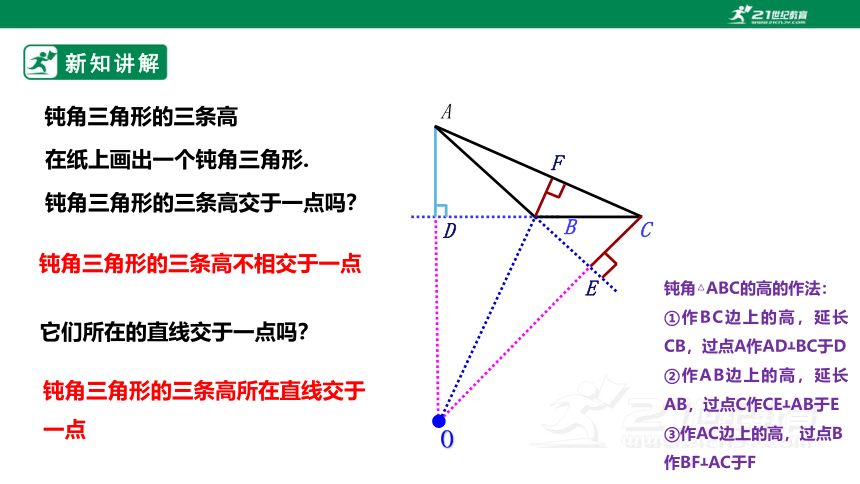
钝角三角形的三条高
钝角三角形的三条高交于一点吗?
它们所在的直线交于一点吗?
O
钝角三角形的三条高不相交于一点
钝角三角形的三条高所在直线交于一点
在纸上画出一个钝角三角形.
钝角△ABC的高的作法:
①作BC边上的高,延长CB,过点A作AD BC于D
②作AB边上的高,延长AB,过点C作CE AB于E
③作AC边上的高,过点B作BF AC于F
新知讲解
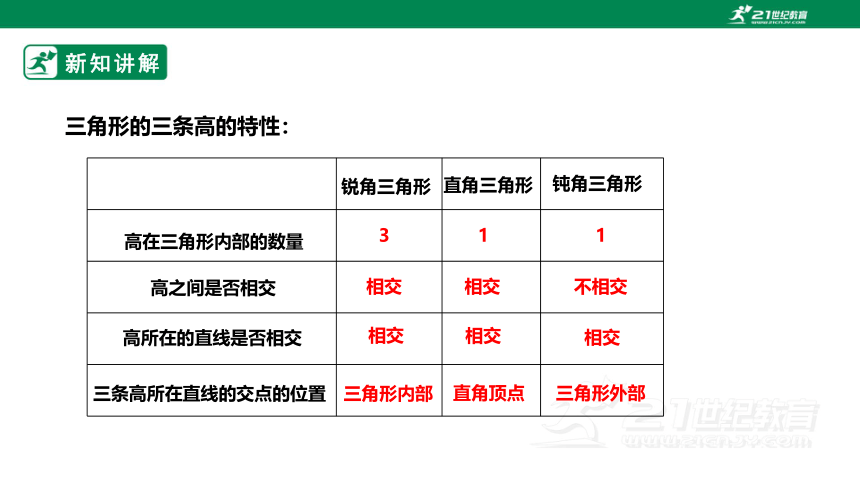
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形内部
直角顶点
三角形外部
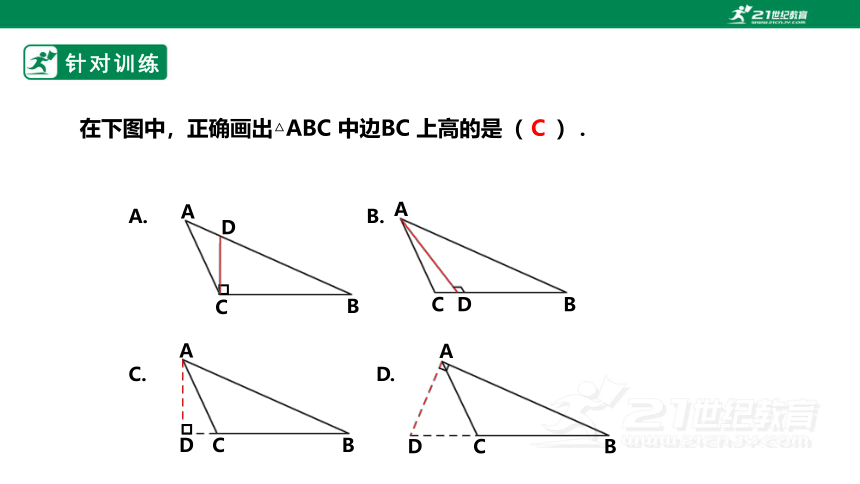
在下图中,正确画出△ABC 中边BC 上高的是( ).
针对训练
C
A. B.
C. D.
A
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
新知讲解
B
A
C
D
·
如图,连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做 △ABC的边BC上的中线.
BD=CD= BC
新知讲解
画一画:如图,分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?
如图,三角形的三条中线相交于一点.三角形三条中线的交点叫做三角形的重心.
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
如图,AD,BE,CF 是△ABC 的三条中线.
(1)AC = ; AE = EC;
CD = ;AG= GD.
(2)若S△ABC = 12 cm2,
则S△ABD = ,S△GBD = .
针对训练
2
2
BD
6 cm
A
B
C
D
E
F
G
2cm
2
总结发现:
重心将三角形面积平均分成六份,将中线分成2:1两部分。
新知讲解
如图,在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
A
B
C
D
●
●
︶
︶
1
2
因为AD是△ABC的角平分线,
所以∠BAD =∠CAD =
∠BAC.
新知讲解
任意剪一个三角形,用折叠的方法,画出这个三角形的三条角平分线,你发现了什么?
三角形的三条角平分线交于同一点.
课堂练习
1. 如图,在△ABC中,若∠BAD=∠DAE=∠EAF=∠FAC,则_____是△ABC的角平分线( )
A. AD B. AE
C. AF D. AC
B
2. 如图,在△ABC中,BC边上的高为( )
A. BF B. CF
C. BD D. AE
D
课堂练习
3. 下列说法错误的是( )
A.锐角三角形的三条高、三条中线、三条角平分线分别交于一点
B.钝角三角形有两条高线三角形外部
C.直角三角形只有一条高
D.任意三角形都有三条高、三条中线、三条角平分线
C
4. 如图,在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△ABC=8 cm2,则阴影部分的面积为______cm2.
2
课堂练习
5. 如图,在△ABC中,AD⊥BC,AE平分∠BAC.若∠1=30°,∠2=20°,则∠B=______.
6. 如图,已知在△ABC中,CF,BE分别是AB,AC边上的中线.若AE=2,AF=3,且△ABC的周长为15,则BC的长为_____.
50°
5
课堂练习
7. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°. 求:
(1)∠BAE的度数;
解:(1)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C=180°-70°-30°=80°.
∵AE平分∠BAC,
∴∠BAE= ∠BAC=40°.
课堂练习
7. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°. 求:
(2)∠DAE的度数;
(2)∵AD⊥BC,
∴∠ADB=90°.
又∵∠ADB=180°-(∠B+∠BAD),
∴∠BAD=90°-∠B=90°-70°=20°.
∴∠DAE=∠BAE-∠BAD=40°-20°=20°.
课堂总结
三角形重要线段
高
锐角三角形的三条高交于同一点,都在三角形的内部.
直角三角形的三条高交于直角顶点.
钝角三角形的三条高不相交于一点,三条高所在直线交于一点.
中线
角平分线
三角形的三条中线相交于一点.三角形三条中线的交点叫做三角形的重心.
三角形的三条角平分线交于同一点.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
11.1.2三角形的高、中线与角平分线
人教版 八年级上册
教学目标
教学目标:
(1)理解三角形的高、中线与角平分线的概念;
(2)会画三角形的高、中线与角平分线;
(3)三角形在实际生活中的应用.
重点:(1)了解三角形的高、中线与角平分线的概念,会用工具准确画出三角形的高、中线与角平分线。
(2)了解三角形的三条高、三条中线与三条角平分线分别交于一点。
难点:(1)三角形平分线与角平分线的区别,三角形的高与垂线的区别。
(2)三角形高的画法。
(3)不同的三角形三条高的位置关系。
新知导入
问题 还记得“过一点画已知直线的垂线”吗?
如何画线段的中点,怎样画∠ABC 的角平分线?
●
●
●
A
B
C
●
新知讲解
你能过三角形的一个顶点,你能画出它的对边的垂线吗
如图,线段AD是BC边上的高.
注意:标明垂直的记号和垂足的字母.
定义:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高.
A
B
C
D
垂足
如图,在△ABC 中,AD⊥BC , 点D是垂足,则AD是△ABC的边BC上的高,
此时:∠ADB = ∠ADC = 90°.
新知讲解
锐角三角形的三条高
每人画一个锐角三角形.
(1) 你能画出这个三角形的三条高吗
(2) 这三条高之间有怎样的位置关系?
O
锐角三角形的三条高是在三角形的内部还是外部
A
B
C
D
E
F
锐角三角形的三条高交于同一点.
锐角三角形的三条高都在三角形的内部.
新知讲解
直角三角形的三条高
在纸上画出一个直角三角形.
A
B
C
(1)画出直角三角形的三条高.
直角边BC边上的高是______;
AB
直角边AB边上的高是______;
CB
(2)它们有怎样的位置关系?
D
斜边AC边上的高是_______.
BD
●
直角三角形的三条高交于直角顶点.
新知讲解
A
B
C
D
E
F
钝角三角形的三条高
钝角三角形的三条高交于一点吗?
它们所在的直线交于一点吗?
O
钝角三角形的三条高不相交于一点
钝角三角形的三条高所在直线交于一点
在纸上画出一个钝角三角形.
钝角△ABC的高的作法:
①作BC边上的高,延长CB,过点A作AD BC于D
②作AB边上的高,延长AB,过点C作CE AB于E
③作AC边上的高,过点B作BF AC于F
新知讲解
三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形内部
直角顶点
三角形外部
在下图中,正确画出△ABC 中边BC 上高的是( ).
针对训练
C
A. B.
C. D.
A
D
C
B
A
D
C
B
A
D
C
B
A
D
C
B
新知讲解
B
A
C
D
·
如图,连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做 △ABC的边BC上的中线.
BD=CD= BC
新知讲解
画一画:如图,分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?
如图,三角形的三条中线相交于一点.三角形三条中线的交点叫做三角形的重心.
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
如图,AD,BE,CF 是△ABC 的三条中线.
(1)AC = ; AE = EC;
CD = ;AG= GD.
(2)若S△ABC = 12 cm2,
则S△ABD = ,S△GBD = .
针对训练
2
2
BD
6 cm
A
B
C
D
E
F
G
2cm
2
总结发现:
重心将三角形面积平均分成六份,将中线分成2:1两部分。
新知讲解
如图,在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线.
A
B
C
D
●
●
︶
︶
1
2
因为AD是△ABC的角平分线,
所以∠BAD =∠CAD =
∠BAC.
新知讲解
任意剪一个三角形,用折叠的方法,画出这个三角形的三条角平分线,你发现了什么?
三角形的三条角平分线交于同一点.
课堂练习
1. 如图,在△ABC中,若∠BAD=∠DAE=∠EAF=∠FAC,则_____是△ABC的角平分线( )
A. AD B. AE
C. AF D. AC
B
2. 如图,在△ABC中,BC边上的高为( )
A. BF B. CF
C. BD D. AE
D
课堂练习
3. 下列说法错误的是( )
A.锐角三角形的三条高、三条中线、三条角平分线分别交于一点
B.钝角三角形有两条高线三角形外部
C.直角三角形只有一条高
D.任意三角形都有三条高、三条中线、三条角平分线
C
4. 如图,在△ABC中,点D,E,F分别为BC,AD,CE的中点,且S△ABC=8 cm2,则阴影部分的面积为______cm2.
2
课堂练习
5. 如图,在△ABC中,AD⊥BC,AE平分∠BAC.若∠1=30°,∠2=20°,则∠B=______.
6. 如图,已知在△ABC中,CF,BE分别是AB,AC边上的中线.若AE=2,AF=3,且△ABC的周长为15,则BC的长为_____.
50°
5
课堂练习
7. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°. 求:
(1)∠BAE的度数;
解:(1)∵∠B+∠C+∠BAC=180°,
∴∠BAC=180°-∠B-∠C=180°-70°-30°=80°.
∵AE平分∠BAC,
∴∠BAE= ∠BAC=40°.
课堂练习
7. 如图,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°. 求:
(2)∠DAE的度数;
(2)∵AD⊥BC,
∴∠ADB=90°.
又∵∠ADB=180°-(∠B+∠BAD),
∴∠BAD=90°-∠B=90°-70°=20°.
∴∠DAE=∠BAE-∠BAD=40°-20°=20°.
课堂总结
三角形重要线段
高
锐角三角形的三条高交于同一点,都在三角形的内部.
直角三角形的三条高交于直角顶点.
钝角三角形的三条高不相交于一点,三条高所在直线交于一点.
中线
角平分线
三角形的三条中线相交于一点.三角形三条中线的交点叫做三角形的重心.
三角形的三条角平分线交于同一点.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
