11.2.1与三角形有关的内角 课件(共24张PPT)
文档属性
| 名称 | 11.2.1与三角形有关的内角 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-09-01 13:42:48 | ||
图片预览





文档简介
(共24张PPT)
11.2.1与三角形有关的内角
人教版 八年级上册
教学目标
教学目标:
(1)探究并掌握三角形内角和性质;
(2)能应用三角形内角和性质解决一些简单的实际问题.
重点:三角形内角和定理.
难点:三角形内角和定理的推理的过程.
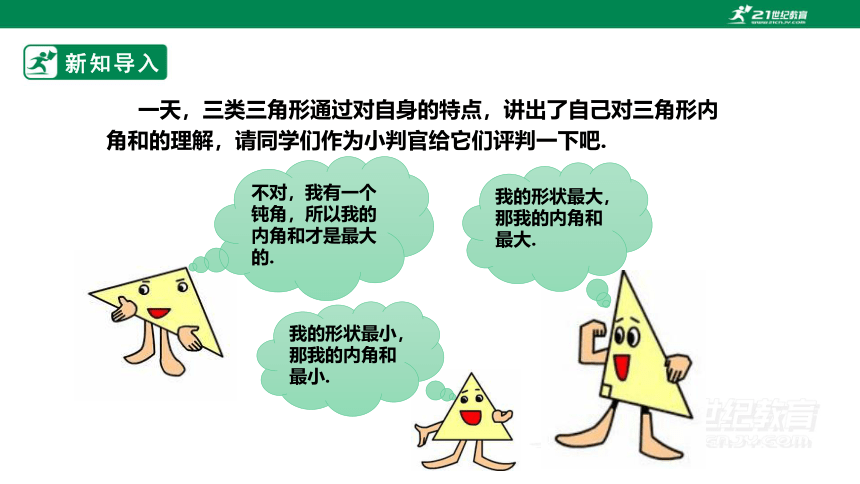
新知导入
我的形状最小,那我的内角和最小.
我的形状最大,那我的内角和最大.
不对,我有一个钝角,所以我的内角和才是最大的.
一天,三类三角形通过对自身的特点,讲出了自己对三角形内角和的理解,请同学们作为小判官给它们评判一下吧.
新知讲解
在小学我们已经知道任意一个三角形三个内角的和等于180°,你还记得是怎么发现这个结论的吗?
方法1:度量
方法2:折叠
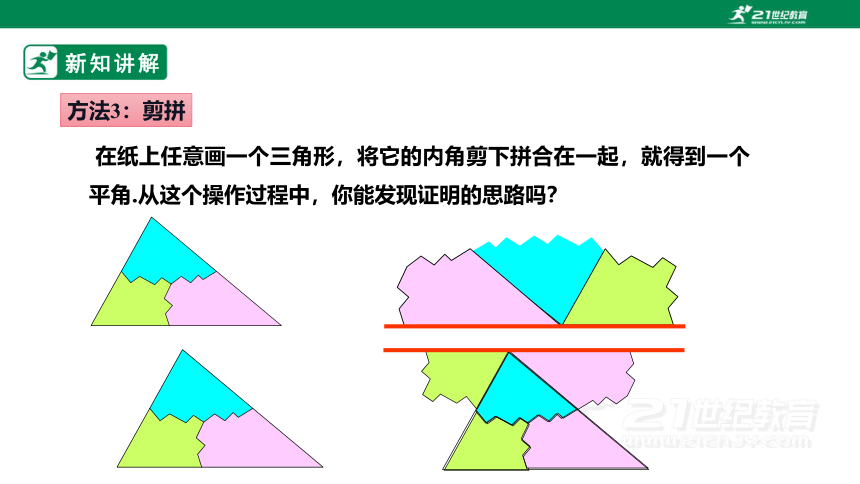
新知讲解
在纸上任意画一个三角形,将它的内角剪下拼合在一起,就得到一个平角.从这个操作过程中,你能发现证明的思路吗?
方法3:剪拼
新知讲解
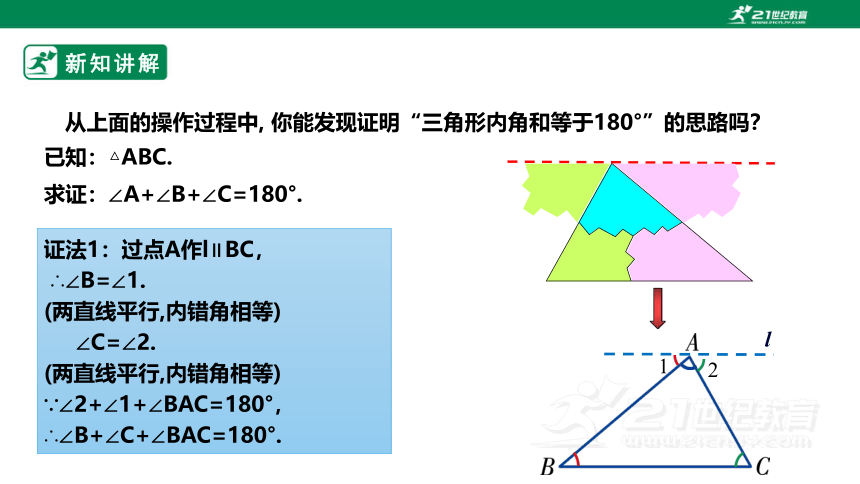
从上面的操作过程中, 你能发现证明“三角形内角和等于180°”的思路吗?
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证法1:过点A作l∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
新知讲解
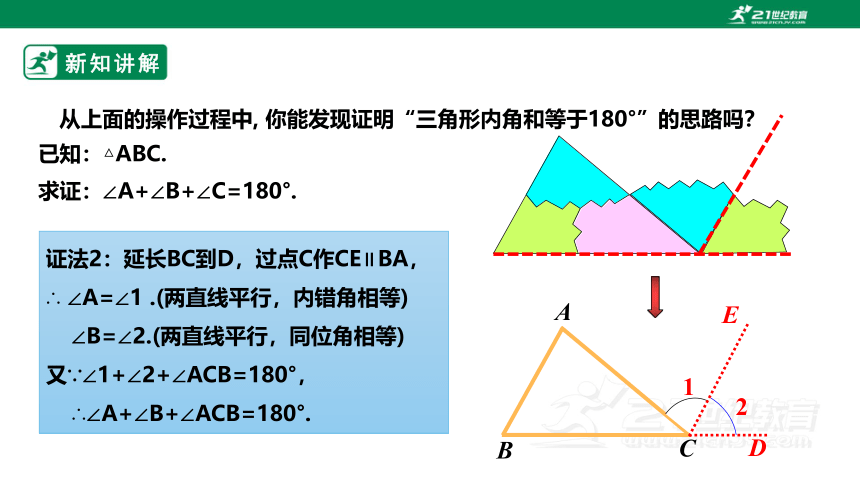
证法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .(两直线平行,内错角相等)
∠B=∠2.(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
从上面的操作过程中, 你能发现证明“三角形内角和等于180°”的思路吗?
求证:∠A+∠B+∠C=180°.
已知:△ABC.
新知讲解
得到如下定理:
三角形内角和定理三角形三个内角的和等于180°.
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线. 在平面几何里,辅助线通常画成虚线.
思路总结:
为了证明三个角的和为180°,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
新知讲解
三角形内角和定理的“三个应用”
1.已知两个角的度数求第三个角的度数.
2.已知一个角的度数求另外两个角度数的和.
3.已知三个角的度数关系,求这三个角的度数.
新知讲解
例1 如图 ,在△ABC 中,∠BAC =40°,∠B = 75°, AD是△ ABC的角平分线.求 ∠ADB 的度数.
C
B
D
A
解:由∠BAC=40°,AD是△ ABC的角平分线,
得∠BAD= ∠BAC=20°.
在△ ABD中,
∠ADB =180°-∠B-∠BAD
= 180° - 75°- 20°=85°.
新知讲解
例2 下图是A,B,C三岛的平面图, C岛在A岛的北偏东50°方向,B岛在A岛的北 偏东80°方向,C岛在B岛的北偏西40°方向。从B岛看A,C两岛的视角∠ABC是多少度?从C岛 看A, B两岛的视角∠ ACB呢?
北
北
C
A
B
D
E
分析:A,B,C三岛的连线构成ABC,
所求的∠ACB是△ABC的一个内角.如果能求出∠ CAB, ∠ ABC,就能求出∠ACB.
新知讲解
解:∠CAB=∠BAD - ∠CAD=80°- 50°=30°.
由 AD//BE,得 ∠ BAD +∠ ABE=180°.
所以∠ ABE=180°- ∠BAD = 180°- 80°= 100°,
∠ ABC=∠ ABE - ∠EBC=100° - 40°=60°.
在△ABC中,∠ACB =180°-∠ABC-∠ CAB
= 180°-60°-30°=90°.
答:从B岛看A, C两岛的视角∠ ABC是60°, 从C岛看A, B两岛的视角∠ ACB是90°.
北
北
C
A
B
D
E
新知讲解
观察这两个直角三角形,它们两锐角之和分别为多少?
那对于任意直角三角形,这一结论是否还成立呢?
如图, 在直角三角形ABC中,∠C = 90°,
由三角形内角和定理,
得∠ A+ ∠ B+ ∠ C = 180°,
即∠ A+ ∠ B+90°=180°,
所以∠ A + ∠ B = 90°
A
B
C
新知讲解
A
B
C
直角三角形的两个锐角互余.
应用格式:
在Rt△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt△ABC .
由此,可以得到直角三角形的性质,
新知讲解
例3 如图,∠C=∠D=90°,AD交BC于点E,∠CAE与∠DBE有什么关系?为什么?
解:∠CAE与∠DBE相等.理由如下.
∵在△CAE和△DBE中,
∠C=∠D=90°,∠CEA=∠DEB,
∴∠CAE=90°-∠CEA,
∠DBE=90°-∠DEB,
即∠CAE=∠DBE.
新知讲解
问题:有两个角互余的三角形是直角三角形吗?
如图,在△ABC中, ∠A +∠B=90° , 那么△ABC是直角三角形吗?
在△ABC中,因为 ∠A +∠B +∠C=180°,
又∠A +∠B=90°,
所以∠C=90°.
于是△ABC是直角三角形.
新知讲解
应用格式:
在△ABC 中,
∵∠A +∠B =90°,
∴△ABC 是直角三角形.
有两个角互余的三角形是直角三角形.
A
B
C
由三角形内角和定理可得:
课堂练习
1. 在△ABC中,∠A=40°,∠B=50°,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
B
2. 如图KH11-4-1,在四边形ABCD中,CD∥AB,AC⊥BC,若∠B=50°,则∠DCA等于( )
A.30°
B.35°
C.40°
D.45°
C
课堂练习
3. 如图,把Rt△ABD沿直线AD翻折180°,点B落在点C的位置.若∠B=70°,则∠CAD的度数为 ( )
A. 70°
B. 40°
C. 30°
D. 20°
4. 直角三角形中,一个锐角等于另一个锐角的2倍,
则较小的锐角是______.
30°
D
课堂练习
5. 如图,BD是∠ABC的平分线,CD是∠ACB的平分线,∠BDC=120°,则∠A的度数为( )
A. 40°
B. 50°
C. 60°
D. 75°
C
课堂练习
6. 如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于点E,∠DAC=26°,∠CBE=22°.求∠BAC的度数.
解:∵AD是BC边上的高,
∴∠ADC=90°.
∵∠DAC=26°,
∴∠C=90°-26°=64°.
∵BE平分∠ABC,∠CBE=22°,
∴∠ABC=2∠CBE=2×22°=44°.
∴∠BAC=180°-∠ABC-∠C=72°.
课堂总结
1.三角形的
内角和等于
180 °
证法
应用
作平行线
转化思想
求角度
转化为一个平角
或
同旁内角互补
辅助线
2.直角三角形的性质——两锐角互余.
直角三角形的判定——有两角互余的三角形是直角三角形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
11.2.1与三角形有关的内角
人教版 八年级上册
教学目标
教学目标:
(1)探究并掌握三角形内角和性质;
(2)能应用三角形内角和性质解决一些简单的实际问题.
重点:三角形内角和定理.
难点:三角形内角和定理的推理的过程.
新知导入
我的形状最小,那我的内角和最小.
我的形状最大,那我的内角和最大.
不对,我有一个钝角,所以我的内角和才是最大的.
一天,三类三角形通过对自身的特点,讲出了自己对三角形内角和的理解,请同学们作为小判官给它们评判一下吧.
新知讲解
在小学我们已经知道任意一个三角形三个内角的和等于180°,你还记得是怎么发现这个结论的吗?
方法1:度量
方法2:折叠
新知讲解
在纸上任意画一个三角形,将它的内角剪下拼合在一起,就得到一个平角.从这个操作过程中,你能发现证明的思路吗?
方法3:剪拼
新知讲解
从上面的操作过程中, 你能发现证明“三角形内角和等于180°”的思路吗?
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证法1:过点A作l∥BC,
∴∠B=∠1.
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
新知讲解
证法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 .(两直线平行,内错角相等)
∠B=∠2.(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
从上面的操作过程中, 你能发现证明“三角形内角和等于180°”的思路吗?
求证:∠A+∠B+∠C=180°.
已知:△ABC.
新知讲解
得到如下定理:
三角形内角和定理三角形三个内角的和等于180°.
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线. 在平面几何里,辅助线通常画成虚线.
思路总结:
为了证明三个角的和为180°,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
新知讲解
三角形内角和定理的“三个应用”
1.已知两个角的度数求第三个角的度数.
2.已知一个角的度数求另外两个角度数的和.
3.已知三个角的度数关系,求这三个角的度数.
新知讲解
例1 如图 ,在△ABC 中,∠BAC =40°,∠B = 75°, AD是△ ABC的角平分线.求 ∠ADB 的度数.
C
B
D
A
解:由∠BAC=40°,AD是△ ABC的角平分线,
得∠BAD= ∠BAC=20°.
在△ ABD中,
∠ADB =180°-∠B-∠BAD
= 180° - 75°- 20°=85°.
新知讲解
例2 下图是A,B,C三岛的平面图, C岛在A岛的北偏东50°方向,B岛在A岛的北 偏东80°方向,C岛在B岛的北偏西40°方向。从B岛看A,C两岛的视角∠ABC是多少度?从C岛 看A, B两岛的视角∠ ACB呢?
北
北
C
A
B
D
E
分析:A,B,C三岛的连线构成ABC,
所求的∠ACB是△ABC的一个内角.如果能求出∠ CAB, ∠ ABC,就能求出∠ACB.
新知讲解
解:∠CAB=∠BAD - ∠CAD=80°- 50°=30°.
由 AD//BE,得 ∠ BAD +∠ ABE=180°.
所以∠ ABE=180°- ∠BAD = 180°- 80°= 100°,
∠ ABC=∠ ABE - ∠EBC=100° - 40°=60°.
在△ABC中,∠ACB =180°-∠ABC-∠ CAB
= 180°-60°-30°=90°.
答:从B岛看A, C两岛的视角∠ ABC是60°, 从C岛看A, B两岛的视角∠ ACB是90°.
北
北
C
A
B
D
E
新知讲解
观察这两个直角三角形,它们两锐角之和分别为多少?
那对于任意直角三角形,这一结论是否还成立呢?
如图, 在直角三角形ABC中,∠C = 90°,
由三角形内角和定理,
得∠ A+ ∠ B+ ∠ C = 180°,
即∠ A+ ∠ B+90°=180°,
所以∠ A + ∠ B = 90°
A
B
C
新知讲解
A
B
C
直角三角形的两个锐角互余.
应用格式:
在Rt△ABC 中,
∵ ∠C =90°,
∴ ∠A +∠B =90°.
直角三角形的表示:直角三角形可以用符号“Rt△”表示,直角三角形ABC 可以写成Rt△ABC .
由此,可以得到直角三角形的性质,
新知讲解
例3 如图,∠C=∠D=90°,AD交BC于点E,∠CAE与∠DBE有什么关系?为什么?
解:∠CAE与∠DBE相等.理由如下.
∵在△CAE和△DBE中,
∠C=∠D=90°,∠CEA=∠DEB,
∴∠CAE=90°-∠CEA,
∠DBE=90°-∠DEB,
即∠CAE=∠DBE.
新知讲解
问题:有两个角互余的三角形是直角三角形吗?
如图,在△ABC中, ∠A +∠B=90° , 那么△ABC是直角三角形吗?
在△ABC中,因为 ∠A +∠B +∠C=180°,
又∠A +∠B=90°,
所以∠C=90°.
于是△ABC是直角三角形.
新知讲解
应用格式:
在△ABC 中,
∵∠A +∠B =90°,
∴△ABC 是直角三角形.
有两个角互余的三角形是直角三角形.
A
B
C
由三角形内角和定理可得:
课堂练习
1. 在△ABC中,∠A=40°,∠B=50°,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
B
2. 如图KH11-4-1,在四边形ABCD中,CD∥AB,AC⊥BC,若∠B=50°,则∠DCA等于( )
A.30°
B.35°
C.40°
D.45°
C
课堂练习
3. 如图,把Rt△ABD沿直线AD翻折180°,点B落在点C的位置.若∠B=70°,则∠CAD的度数为 ( )
A. 70°
B. 40°
C. 30°
D. 20°
4. 直角三角形中,一个锐角等于另一个锐角的2倍,
则较小的锐角是______.
30°
D
课堂练习
5. 如图,BD是∠ABC的平分线,CD是∠ACB的平分线,∠BDC=120°,则∠A的度数为( )
A. 40°
B. 50°
C. 60°
D. 75°
C
课堂练习
6. 如图,在△ABC中,AD是BC边上的高,BE平分∠ABC交AC边于点E,∠DAC=26°,∠CBE=22°.求∠BAC的度数.
解:∵AD是BC边上的高,
∴∠ADC=90°.
∵∠DAC=26°,
∴∠C=90°-26°=64°.
∵BE平分∠ABC,∠CBE=22°,
∴∠ABC=2∠CBE=2×22°=44°.
∴∠BAC=180°-∠ABC-∠C=72°.
课堂总结
1.三角形的
内角和等于
180 °
证法
应用
作平行线
转化思想
求角度
转化为一个平角
或
同旁内角互补
辅助线
2.直角三角形的性质——两锐角互余.
直角三角形的判定——有两角互余的三角形是直角三角形.
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
