全国人教版数学八年级下册课课练:17.1 第3课时 利用勾股定理计算、作图(含答案解析)
文档属性
| 名称 | 全国人教版数学八年级下册课课练:17.1 第3课时 利用勾股定理计算、作图(含答案解析) | 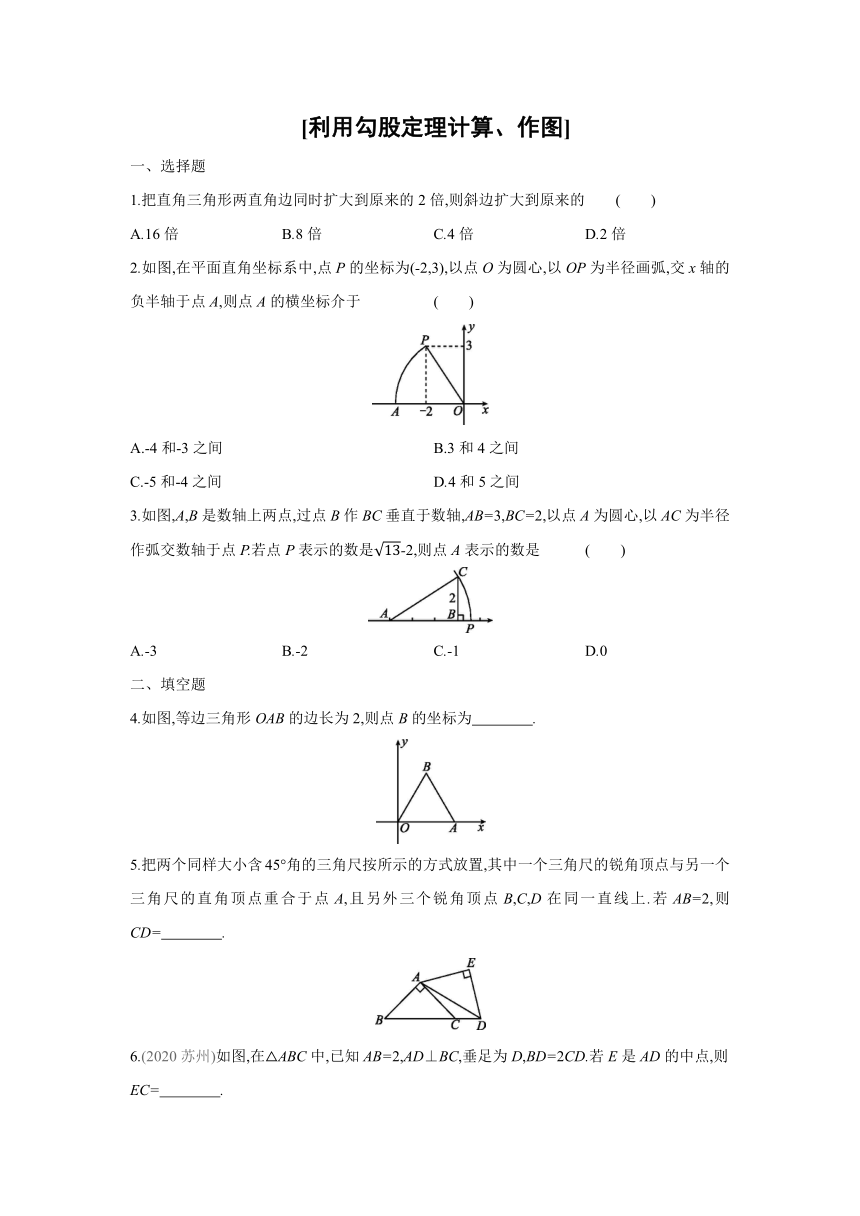 | |
| 格式 | docx | ||
| 文件大小 | 144.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-19 14:22:13 | ||
图片预览


文档简介
[利用勾股定理计算、作图]
一、选择题
1.把直角三角形两直角边同时扩大到原来的2倍,则斜边扩大到原来的 ( )
A.16倍 B.8倍 C.4倍 D.2倍
2.如图,在平面直角坐标系中,点P的坐标为(-2,3),以点O为圆心,以OP为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于 ( )
A.-4和-3之间 B.3和4之间
C.-5和-4之间 D.4和5之间
3.如图,A,B是数轴上两点,过点B作BC垂直于数轴,AB=3,BC=2,以点A为圆心,以AC为半径作弧交数轴于点P.若点P表示的数是-2,则点A表示的数是 ( )
A.-3 B.-2 C.-1 D.0
二、填空题
4.如图,等边三角形OAB的边长为2,则点B的坐标为 .
5.把两个同样大小含45°角的三角尺按所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一直线上.若AB=2,则CD= .
6.(2020苏州)如图,在△ABC中,已知AB=2,AD⊥BC,垂足为D,BD=2CD.若E是AD的中点,则EC= .
三、解答题
7.尺规作图:在数轴上作出表示的点.
作法:
①如图,在数轴上点A,B,C分别表示-2,-1,0,分别以点A,B为圆心,AB为半径画弧,两弧交于点D;
②连接CD,以点C为圆心,CD为半径画弧,交数轴正半轴于点P,则点P表示的数就是无理数.
(1)判断△ACD的形状,并说明理由;
(2)说明点P表示的数就是无理数的理由.
[分类讨论] 有一块直角三角形的绿地,量得两直角边长分别为6 m,8 m.现在要将绿地扩充成等腰三角形,且扩充部分是以8 m的直角边为一边的直角三角形,则扩充后等腰三角形绿地的周长为 .
答案
1.D
2.A ∵点P的坐标为(-2,3),
∴OP==.
∵点A,P均在以点O为圆心,以OP为半径的圆上,∴OA=OP=.
∵9<13<16,∴3<<4.
又∵点A在x轴的负半轴上,
∴点A的横坐标介于-4和-3之间.
故选A.
3.B ∵在Rt△ABC中,AB=3,BC=2,
∴AC==,
∴AP=AC=.
∵点P表示的数是-2,
∴点A表示的数是-2-=-2.
4.(1,) 过点B作OA的垂线,垂足为D,则OD=OA=1,∴BD==,故点B的坐标为(1,).
5.- 在等腰直角三角形ABC中,
∵AB=2,∴BC=2.
如图,过点A作AM⊥BD于点M,则△ABM和△ACM都是等腰直角三角形,
则AM=MC=BM=BC=.
在Rt△AMD中,AD=BC=2,AM=,
∴MD=,∴CD=MD-MC=-.
6.1 设AE=ED=x,CD=y,则BD=2y.
∵AD⊥BC,∴∠ADB=∠ADC=90°.
在Rt△ABD中,
AB2=AD2+BD2=4x2+4y2.
∵AB=2,∴x2+y2=1.
在Rt△CDE中,EC2=CD2+ED2=x2+y2=1,
∴EC=1.
7.解:(1)△ACD是直角三角形.
理由:由题意可得AD=AB=BD=BC=1,
∴△ABD是等边三角形,∠BDC=∠BCD,
∴∠DAB=∠DBA=60°.
∵∠DBA=∠BDC+∠BCD,
∴∠BCD=30°,
∴∠ADC=180°-∠DAB-∠BCD=90°,
∴△ACD是直角三角形.
(2)∵△ACD是直角三角形,AD=1,AC=2,∠ADC=90°,
∴CD===.
∵CD=CP,∴CP=.
∵在数轴上,点C表示的数为0,
∴点P表示的数就是无理数.
[素养提升]
32 m或(20+4)m或 m
在Rt△ABC中,∠ACB=90°,AC=8 m,BC=6 m.
由勾股定理,得AB=10 m.
扩充部分为Rt△ACD,扩充成等腰三角形ABD,应分以下三种情况.
(1)如图甲所示,若AD=AB=10 m,
可求得CD=BC=6 m.
此时△ABD的周长为32 m.
(2)如图乙所示,若BD=AB=10 m,
可求得CD=4 m,由勾股定理,得AD=4 m.
此时△ABD的周长为m.
(3)如图丙所示,若AD=BD,设AD=BD=x m,则CD=(x-6)m.
由勾股定理,得x2=82+(x-6)2,解得x=.
此时△ABD的周长为 m.
综上可知,扩充后等腰三角形绿地的周长为32 m或(20+4)m或 m.
[点评] 在涉及等腰三角形的问题中,往往需要分类讨论求解,否则容易漏解.
一、选择题
1.把直角三角形两直角边同时扩大到原来的2倍,则斜边扩大到原来的 ( )
A.16倍 B.8倍 C.4倍 D.2倍
2.如图,在平面直角坐标系中,点P的坐标为(-2,3),以点O为圆心,以OP为半径画弧,交x轴的负半轴于点A,则点A的横坐标介于 ( )
A.-4和-3之间 B.3和4之间
C.-5和-4之间 D.4和5之间
3.如图,A,B是数轴上两点,过点B作BC垂直于数轴,AB=3,BC=2,以点A为圆心,以AC为半径作弧交数轴于点P.若点P表示的数是-2,则点A表示的数是 ( )
A.-3 B.-2 C.-1 D.0
二、填空题
4.如图,等边三角形OAB的边长为2,则点B的坐标为 .
5.把两个同样大小含45°角的三角尺按所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一直线上.若AB=2,则CD= .
6.(2020苏州)如图,在△ABC中,已知AB=2,AD⊥BC,垂足为D,BD=2CD.若E是AD的中点,则EC= .
三、解答题
7.尺规作图:在数轴上作出表示的点.
作法:
①如图,在数轴上点A,B,C分别表示-2,-1,0,分别以点A,B为圆心,AB为半径画弧,两弧交于点D;
②连接CD,以点C为圆心,CD为半径画弧,交数轴正半轴于点P,则点P表示的数就是无理数.
(1)判断△ACD的形状,并说明理由;
(2)说明点P表示的数就是无理数的理由.
[分类讨论] 有一块直角三角形的绿地,量得两直角边长分别为6 m,8 m.现在要将绿地扩充成等腰三角形,且扩充部分是以8 m的直角边为一边的直角三角形,则扩充后等腰三角形绿地的周长为 .
答案
1.D
2.A ∵点P的坐标为(-2,3),
∴OP==.
∵点A,P均在以点O为圆心,以OP为半径的圆上,∴OA=OP=.
∵9<13<16,∴3<<4.
又∵点A在x轴的负半轴上,
∴点A的横坐标介于-4和-3之间.
故选A.
3.B ∵在Rt△ABC中,AB=3,BC=2,
∴AC==,
∴AP=AC=.
∵点P表示的数是-2,
∴点A表示的数是-2-=-2.
4.(1,) 过点B作OA的垂线,垂足为D,则OD=OA=1,∴BD==,故点B的坐标为(1,).
5.- 在等腰直角三角形ABC中,
∵AB=2,∴BC=2.
如图,过点A作AM⊥BD于点M,则△ABM和△ACM都是等腰直角三角形,
则AM=MC=BM=BC=.
在Rt△AMD中,AD=BC=2,AM=,
∴MD=,∴CD=MD-MC=-.
6.1 设AE=ED=x,CD=y,则BD=2y.
∵AD⊥BC,∴∠ADB=∠ADC=90°.
在Rt△ABD中,
AB2=AD2+BD2=4x2+4y2.
∵AB=2,∴x2+y2=1.
在Rt△CDE中,EC2=CD2+ED2=x2+y2=1,
∴EC=1.
7.解:(1)△ACD是直角三角形.
理由:由题意可得AD=AB=BD=BC=1,
∴△ABD是等边三角形,∠BDC=∠BCD,
∴∠DAB=∠DBA=60°.
∵∠DBA=∠BDC+∠BCD,
∴∠BCD=30°,
∴∠ADC=180°-∠DAB-∠BCD=90°,
∴△ACD是直角三角形.
(2)∵△ACD是直角三角形,AD=1,AC=2,∠ADC=90°,
∴CD===.
∵CD=CP,∴CP=.
∵在数轴上,点C表示的数为0,
∴点P表示的数就是无理数.
[素养提升]
32 m或(20+4)m或 m
在Rt△ABC中,∠ACB=90°,AC=8 m,BC=6 m.
由勾股定理,得AB=10 m.
扩充部分为Rt△ACD,扩充成等腰三角形ABD,应分以下三种情况.
(1)如图甲所示,若AD=AB=10 m,
可求得CD=BC=6 m.
此时△ABD的周长为32 m.
(2)如图乙所示,若BD=AB=10 m,
可求得CD=4 m,由勾股定理,得AD=4 m.
此时△ABD的周长为m.
(3)如图丙所示,若AD=BD,设AD=BD=x m,则CD=(x-6)m.
由勾股定理,得x2=82+(x-6)2,解得x=.
此时△ABD的周长为 m.
综上可知,扩充后等腰三角形绿地的周长为32 m或(20+4)m或 m.
[点评] 在涉及等腰三角形的问题中,往往需要分类讨论求解,否则容易漏解.
