全国人教版数学八年级下册课课练:18章 平行四边形 单元复习训练(含答案解析)
文档属性
| 名称 | 全国人教版数学八年级下册课课练:18章 平行四边形 单元复习训练(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 177.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 12:05:54 | ||
图片预览


文档简介
第18章单元复习训练
一、选择题
1.(2021宜宾)下列说法正确的是 ( )
A.平行四边形是轴对称图形
B.平行四边形的邻边相等
C.平行四边形的对角线互相垂直
D.平行四边形的对角线互相平分
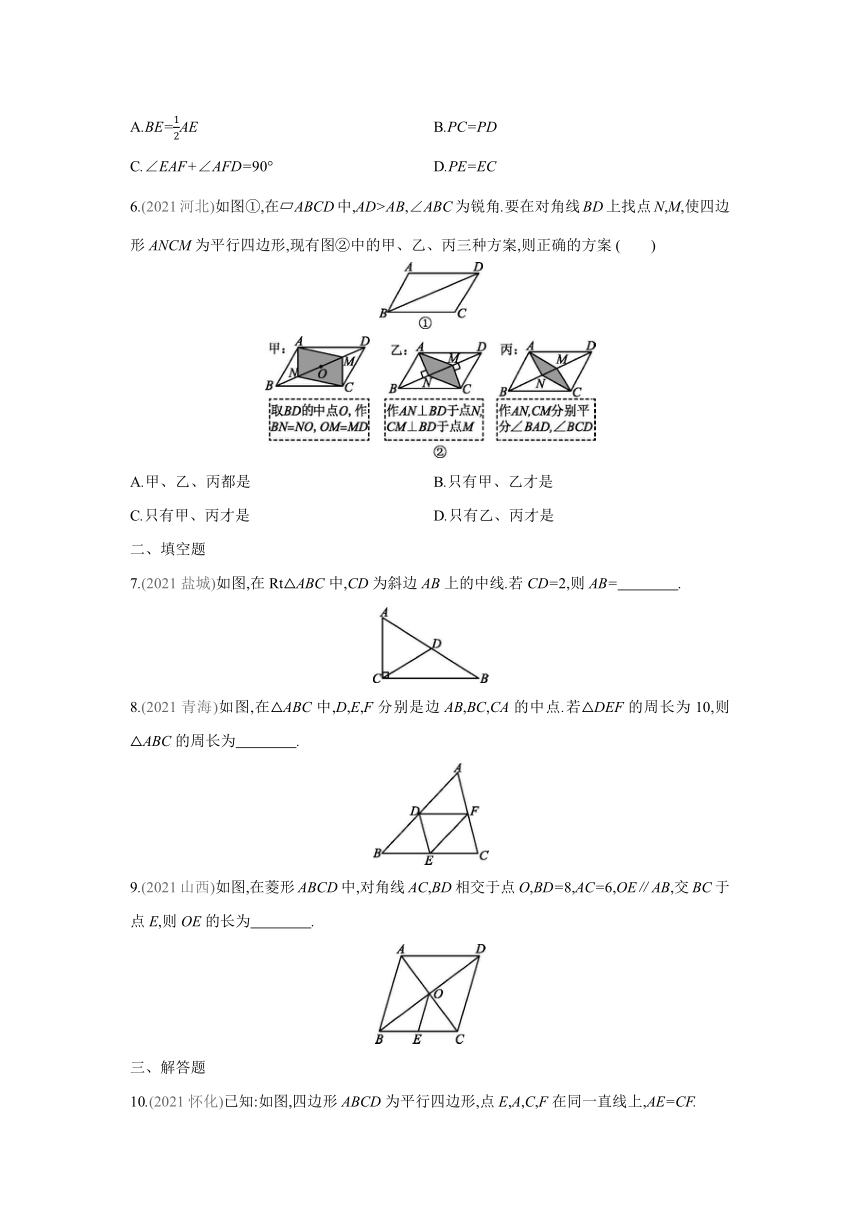
2.(2021株洲)如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上.若∠DCE=132°,则∠A的度数为 ( )
A.38° B.48° C.58° D.66°
3.(2021恩施州)如图,在 ABCD中,AB=13,AD=5,AC⊥BC,则 ABCD的面积为 ( )
A.30 B.60 C.65 D.
4.(2021安顺)如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F.若AB=3,AD=4,则EF的长是 ( )
A.1 B.2 C.2.5 D.3
5.(2021常德)如图,已知F,E分别是正方形ABCD的边AB与BC的中点,AE与DF相交于点P,连接PC,则下列结论成立的是 ( )
A.BE=AE B.PC=PD
C.∠EAF+∠AFD=90° D.PE=EC
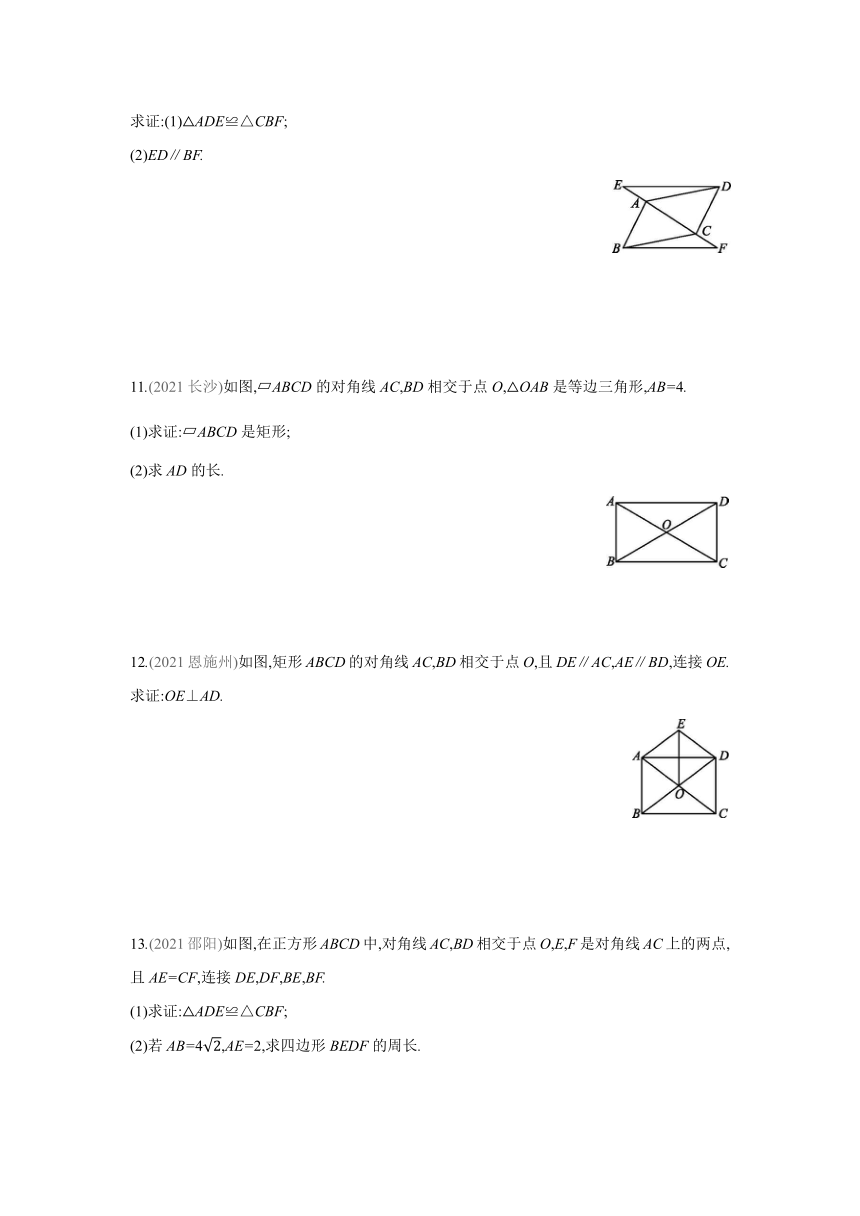
6.(2021河北)如图①,在 ABCD中,AD>AB,∠ABC为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图②中的甲、乙、丙三种方案,则正确的方案 ( )
A.甲、乙、丙都是 B.只有甲、乙才是
C.只有甲、丙才是 D.只有乙、丙才是
二、填空题
7.(2021盐城)如图,在Rt△ABC中,CD为斜边AB上的中线.若CD=2,则AB= .
8.(2021青海)如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点.若△DEF的周长为10,则△ABC的周长为 .
9.(2021山西)如图,在菱形ABCD中,对角线AC,BD相交于点O,BD=8,AC=6,OE∥AB,交BC于点E,则OE的长为 .
三、解答题
10.(2021怀化)已知:如图,四边形ABCD为平行四边形,点E,A,C,F在同一直线上,AE=CF.
求证:(1)△ADE≌△CBF;
(2)ED∥BF.
11.(2021长沙)如图, ABCD的对角线AC,BD相交于点O,△OAB是等边三角形,AB=4.
(1)求证: ABCD是矩形;
(2)求AD的长.
12.(2021恩施州)如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD,连接OE.求证:OE⊥AD.
13.(2021邵阳)如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,且AE=CF,连接DE,DF,BE,BF.
(1)求证:△ADE≌△CBF;
(2)若AB=4,AE=2,求四边形BEDF的周长.
答案
1.D 2.B 3.B
4.B ∵四边形ABCD是平行四边形,
∴AD∥CB,AB=CD=3,AD=BC=4,
∴∠DFC=∠FCB.
∵CF平分∠BCD,
∴∠DCF=∠FCB,∴∠DFC=∠DCF,
∴DF=DC=3.同理可得AE=AB=3.
∵AD=4,∴AF=4-3=1,DE=4-3=1,
∴EF=4-1-1=2.
5.C ∵F,E分别是正方形ABCD的边AB与BC的中点,
∴AF=BE.
又∵∠DAF=∠ABE=90°,AD=BA,
∴△AFD≌△BEA(SAS),
∴∠FDA=∠EAB.
又∵∠FDA+∠AFD=90°,
∴∠EAB+∠AFD=90°,
即∠EAF+∠AFD=90°.
其他选项不能得到.
6.A 方案甲中,连接AC,如图所示.
∵四边形ABCD是平行四边形,O为BD的中点,则点O在AC上,
∴OB=OD,OA=OC.
∵BN=NO,OM=MD,∴NO=OM,
∴四边形ANCM为平行四边形.故方案甲正确;
方案乙中:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∴∠ABN=∠CDM.
∵AN⊥BD于点N,CM⊥BD于点M,
∴AN∥CM,∠ANB=∠CMD=90°,
∴△ABN≌△CDM(AAS),∴AN=CM.
又∵AN∥CM,∴四边形ANCM为平行四边形.故方案乙正确;
方案丙中:∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,AB=CD,AB∥CD,
∴∠ABN=∠CDM.
∵AN平分∠BAD,CM平分∠BCD,
∴∠BAN=∠BAD,∠DCM=∠BCD,
∴∠BAN=∠DCM,
∴△ABN≌△CDM(ASA),
∴AN=CM,∠ANB=∠CMD,
∴∠ANM=∠CMN,∴AN∥CM,
∴四边形ANCM为平行四边形.故方案丙正确.
7.4
8.20 ∵D,E,F分别是△ABC的边AB,BC,CA的中点,
∴EF,DE,DF为△ABC的中位线,
∴EF=AB,DF=BC,DE=AC,
∴AB=2EF,BC=2DF,AC=2DE.
∵△DEF的周长为10,
∴EF+DF+DE=10,
∴2EF+2DF+2DE=20,
∴AB+BC+AC=20,
∴△ABC的周长为20.
9. ∵在菱形ABCD中,对角线AC,BD相交于点O,
∴OA=OC=AC=3,OB=BD=4,AC⊥BD.
∵OE∥AB,OA=OC,
∴OE为△ABC的中位线,
∴OE=AB.
在Rt△ABO中,由勾股定理,得AB===5,
∴OE=.
10.证明:(1)∵四边形ABCD为平行四边形,
∴DA=BC,DA∥BC,
∴∠DAC=∠BCA.
∵∠DAC+∠EAD=180°,∠BCA+∠FCB=180°,
∴∠EAD=∠FCB.
又∵AE=CF,
∴△ADE≌△CBF(SAS).
(2)由(1)知,△ADE≌△CBF,
∴∠E=∠F,
∴ED∥BF.
11.解:(1)证明:∵△OAB为等边三角形,
∴∠ABO=60°,OA=OB.
∵四边形ABCD是平行四边形,
∴OB=OD=BD,OA=OC=AC,
∴BD=AC,∴ ABCD是矩形.
(2)∵ ABCD是矩形,∴∠BAD=90°.
∵∠ABO=60°,∴∠ADB=30°,
∴BD=2AB=8,
∴AD==4.
12.证明:∵四边形ABCD为矩形,
∴AC与BD相等且互相平分,∴OA=OD.
∵DE∥AC,AE∥BD,
∴四边形AODE为平行四边形.
又∵OA=OD,
∴平行四边形AODE为菱形,
∴OE⊥AD.
13.解:(1)证明:∵四边形ABCD是正方形,
∴∠DAE=∠BCF=45°,AD=CB.
又∵AE=CF,
∴△ADE≌△CBF(SAS).
(2)∵AB=4,AB=AD,∠BAD=90°,
∴BD==8.
由正方形对角线相等且互相垂直平分可得:
AC⊥BD,AC=BD=8,OD=OB=4,OA=OC=4.
又AE=CF=2,
∴OA-AE=OC-CF,
即OE=OF=4-2=2,
故四边形BEDF为菱形.
∵∠DOE=90°,
∴DE==2,
故四边形BEDF的周长为4DE=4×2=8.
一、选择题
1.(2021宜宾)下列说法正确的是 ( )
A.平行四边形是轴对称图形
B.平行四边形的邻边相等
C.平行四边形的对角线互相垂直
D.平行四边形的对角线互相平分
2.(2021株洲)如图所示,四边形ABCD是平行四边形,点E在线段BC的延长线上.若∠DCE=132°,则∠A的度数为 ( )
A.38° B.48° C.58° D.66°
3.(2021恩施州)如图,在 ABCD中,AB=13,AD=5,AC⊥BC,则 ABCD的面积为 ( )
A.30 B.60 C.65 D.
4.(2021安顺)如图,在 ABCD中,∠ABC的平分线交AD于点E,∠BCD的平分线交AD于点F.若AB=3,AD=4,则EF的长是 ( )
A.1 B.2 C.2.5 D.3
5.(2021常德)如图,已知F,E分别是正方形ABCD的边AB与BC的中点,AE与DF相交于点P,连接PC,则下列结论成立的是 ( )
A.BE=AE B.PC=PD
C.∠EAF+∠AFD=90° D.PE=EC
6.(2021河北)如图①,在 ABCD中,AD>AB,∠ABC为锐角.要在对角线BD上找点N,M,使四边形ANCM为平行四边形,现有图②中的甲、乙、丙三种方案,则正确的方案 ( )
A.甲、乙、丙都是 B.只有甲、乙才是
C.只有甲、丙才是 D.只有乙、丙才是
二、填空题
7.(2021盐城)如图,在Rt△ABC中,CD为斜边AB上的中线.若CD=2,则AB= .
8.(2021青海)如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点.若△DEF的周长为10,则△ABC的周长为 .
9.(2021山西)如图,在菱形ABCD中,对角线AC,BD相交于点O,BD=8,AC=6,OE∥AB,交BC于点E,则OE的长为 .
三、解答题
10.(2021怀化)已知:如图,四边形ABCD为平行四边形,点E,A,C,F在同一直线上,AE=CF.
求证:(1)△ADE≌△CBF;
(2)ED∥BF.
11.(2021长沙)如图, ABCD的对角线AC,BD相交于点O,△OAB是等边三角形,AB=4.
(1)求证: ABCD是矩形;
(2)求AD的长.
12.(2021恩施州)如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,AE∥BD,连接OE.求证:OE⊥AD.
13.(2021邵阳)如图,在正方形ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,且AE=CF,连接DE,DF,BE,BF.
(1)求证:△ADE≌△CBF;
(2)若AB=4,AE=2,求四边形BEDF的周长.
答案
1.D 2.B 3.B
4.B ∵四边形ABCD是平行四边形,
∴AD∥CB,AB=CD=3,AD=BC=4,
∴∠DFC=∠FCB.
∵CF平分∠BCD,
∴∠DCF=∠FCB,∴∠DFC=∠DCF,
∴DF=DC=3.同理可得AE=AB=3.
∵AD=4,∴AF=4-3=1,DE=4-3=1,
∴EF=4-1-1=2.
5.C ∵F,E分别是正方形ABCD的边AB与BC的中点,
∴AF=BE.
又∵∠DAF=∠ABE=90°,AD=BA,
∴△AFD≌△BEA(SAS),
∴∠FDA=∠EAB.
又∵∠FDA+∠AFD=90°,
∴∠EAB+∠AFD=90°,
即∠EAF+∠AFD=90°.
其他选项不能得到.
6.A 方案甲中,连接AC,如图所示.
∵四边形ABCD是平行四边形,O为BD的中点,则点O在AC上,
∴OB=OD,OA=OC.
∵BN=NO,OM=MD,∴NO=OM,
∴四边形ANCM为平行四边形.故方案甲正确;
方案乙中:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,∴∠ABN=∠CDM.
∵AN⊥BD于点N,CM⊥BD于点M,
∴AN∥CM,∠ANB=∠CMD=90°,
∴△ABN≌△CDM(AAS),∴AN=CM.
又∵AN∥CM,∴四边形ANCM为平行四边形.故方案乙正确;
方案丙中:∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,AB=CD,AB∥CD,
∴∠ABN=∠CDM.
∵AN平分∠BAD,CM平分∠BCD,
∴∠BAN=∠BAD,∠DCM=∠BCD,
∴∠BAN=∠DCM,
∴△ABN≌△CDM(ASA),
∴AN=CM,∠ANB=∠CMD,
∴∠ANM=∠CMN,∴AN∥CM,
∴四边形ANCM为平行四边形.故方案丙正确.
7.4
8.20 ∵D,E,F分别是△ABC的边AB,BC,CA的中点,
∴EF,DE,DF为△ABC的中位线,
∴EF=AB,DF=BC,DE=AC,
∴AB=2EF,BC=2DF,AC=2DE.
∵△DEF的周长为10,
∴EF+DF+DE=10,
∴2EF+2DF+2DE=20,
∴AB+BC+AC=20,
∴△ABC的周长为20.
9. ∵在菱形ABCD中,对角线AC,BD相交于点O,
∴OA=OC=AC=3,OB=BD=4,AC⊥BD.
∵OE∥AB,OA=OC,
∴OE为△ABC的中位线,
∴OE=AB.
在Rt△ABO中,由勾股定理,得AB===5,
∴OE=.
10.证明:(1)∵四边形ABCD为平行四边形,
∴DA=BC,DA∥BC,
∴∠DAC=∠BCA.
∵∠DAC+∠EAD=180°,∠BCA+∠FCB=180°,
∴∠EAD=∠FCB.
又∵AE=CF,
∴△ADE≌△CBF(SAS).
(2)由(1)知,△ADE≌△CBF,
∴∠E=∠F,
∴ED∥BF.
11.解:(1)证明:∵△OAB为等边三角形,
∴∠ABO=60°,OA=OB.
∵四边形ABCD是平行四边形,
∴OB=OD=BD,OA=OC=AC,
∴BD=AC,∴ ABCD是矩形.
(2)∵ ABCD是矩形,∴∠BAD=90°.
∵∠ABO=60°,∴∠ADB=30°,
∴BD=2AB=8,
∴AD==4.
12.证明:∵四边形ABCD为矩形,
∴AC与BD相等且互相平分,∴OA=OD.
∵DE∥AC,AE∥BD,
∴四边形AODE为平行四边形.
又∵OA=OD,
∴平行四边形AODE为菱形,
∴OE⊥AD.
13.解:(1)证明:∵四边形ABCD是正方形,
∴∠DAE=∠BCF=45°,AD=CB.
又∵AE=CF,
∴△ADE≌△CBF(SAS).
(2)∵AB=4,AB=AD,∠BAD=90°,
∴BD==8.
由正方形对角线相等且互相垂直平分可得:
AC⊥BD,AC=BD=8,OD=OB=4,OA=OC=4.
又AE=CF=2,
∴OA-AE=OC-CF,
即OE=OF=4-2=2,
故四边形BEDF为菱形.
∵∠DOE=90°,
∴DE==2,
故四边形BEDF的周长为4DE=4×2=8.
