全国人教版数学八年级下册课课练:第18章 平行四边形 综合检测(word版含答案)
文档属性
| 名称 | 全国人教版数学八年级下册课课练:第18章 平行四边形 综合检测(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 213.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 17:45:38 | ||
图片预览


文档简介
第十八章综合检测
[测试范围:平行四边形 时间:90分钟 分值:100分]
一、选择题(每小题3分,共30分)
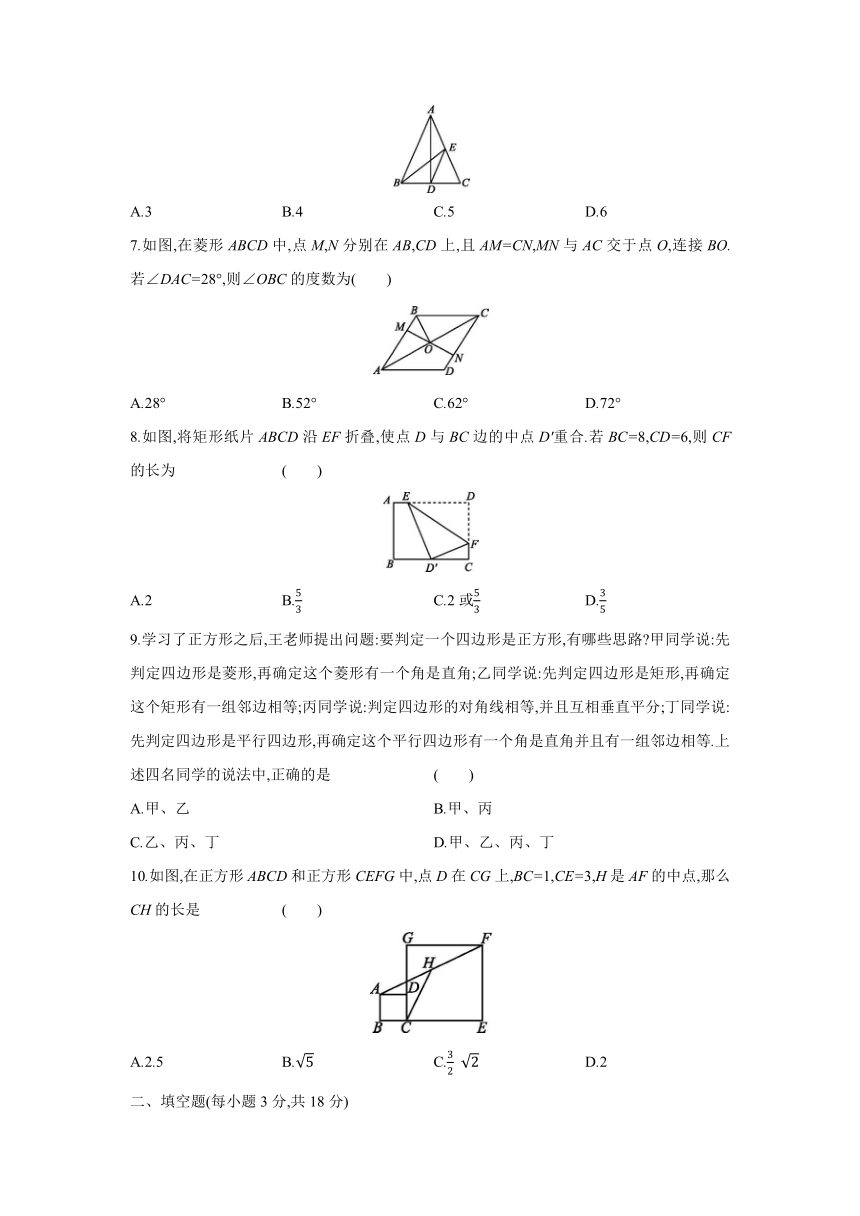
1.如图,直线a∥b,点A,C在直线a上,点B,D在直线b上,则直线a,b之间的距离是 ( )
A.线段AB的长度 B.线段AB
C.线段CD的长度 D.线段CD
2.如图所示的矩形是轴对称图形,对称轴可能是 ( )
A.直线l1 B.直线l2 C.直线l3 D.直线l4
3.在 ABCD中,∠A比∠B小20°,则∠C的度数为 ( )
A.60° B.80° C.100° D.120°
4.如图,在四边形ABCD中,对角线AC与BD相交于点O,下列条件中不能判定四边形ABCD是平行四边形的是 ( )
A.OA=OC,OB=OD B.AB∥CD,AD∥CB
C.AB=CD,AD=CB D.AB∥CD,AD=CB
5.如图,D,E分别为△ABC的边AC,BC的中点,∠A=60°,DE=6,则下列判断错误的是 ( )
A.∠ADE=120° B.AB=12 C.∠CDE=60° D.DC=6
6.如图,在△ABC中,AB=AC=8,AD是角平分线,BE是中线,则DE的长为 ( )
A.3 B.4 C.5 D.6
7.如图,在菱形ABCD中,点M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
8.如图,将矩形纸片ABCD沿EF折叠,使点D与BC边的中点D'重合.若BC=8,CD=6,则CF的长为 ( )
A.2 B. C.2或 D.
9.学习了正方形之后,王老师提出问题:要判定一个四边形是正方形,有哪些思路 甲同学说:先判定四边形是菱形,再确定这个菱形有一个角是直角;乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等;丙同学说:判定四边形的对角线相等,并且互相垂直平分;丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等.上述四名同学的说法中,正确的是 ( )
A.甲、乙 B.甲、丙
C.乙、丙、丁 D.甲、乙、丙、丁
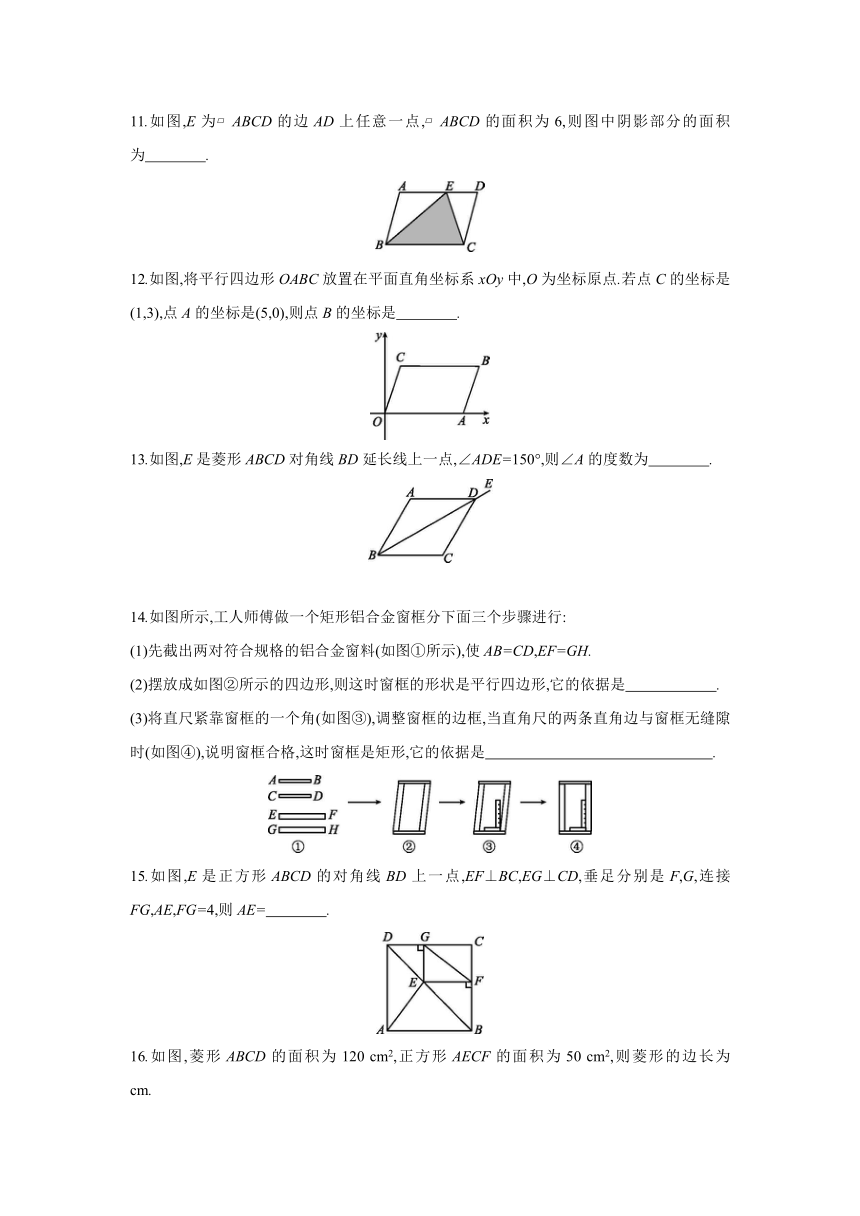
10.如图,在正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 ( )
A.2.5 B. C. D.2
二、填空题(每小题3分,共18分)
11.如图,E为 ABCD的边AD上任意一点, ABCD的面积为6,则图中阴影部分的面积为 .
12.如图,将平行四边形OABC放置在平面直角坐标系xOy中,O为坐标原点.若点C的坐标是(1,3),点A的坐标是(5,0),则点B的坐标是 .
13.如图,E是菱形ABCD对角线BD延长线上一点,∠ADE=150°,则∠A的度数为 .
14.如图所示,工人师傅做一个矩形铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图①所示),使AB=CD,EF=GH.
(2)摆放成如图②所示的四边形,则这时窗框的形状是平行四边形,它的依据是 .
(3)将直尺紧靠窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是矩形,它的依据是 .
15.如图,E是正方形ABCD的对角线BD上一点,EF⊥BC,EG⊥CD,垂足分别是F,G,连接FG,AE,FG=4,则AE= .
16.如图,菱形ABCD的面积为120 cm2,正方形AECF的面积为50 cm2,则菱形的边长为 cm.
三、解答题(共52分)
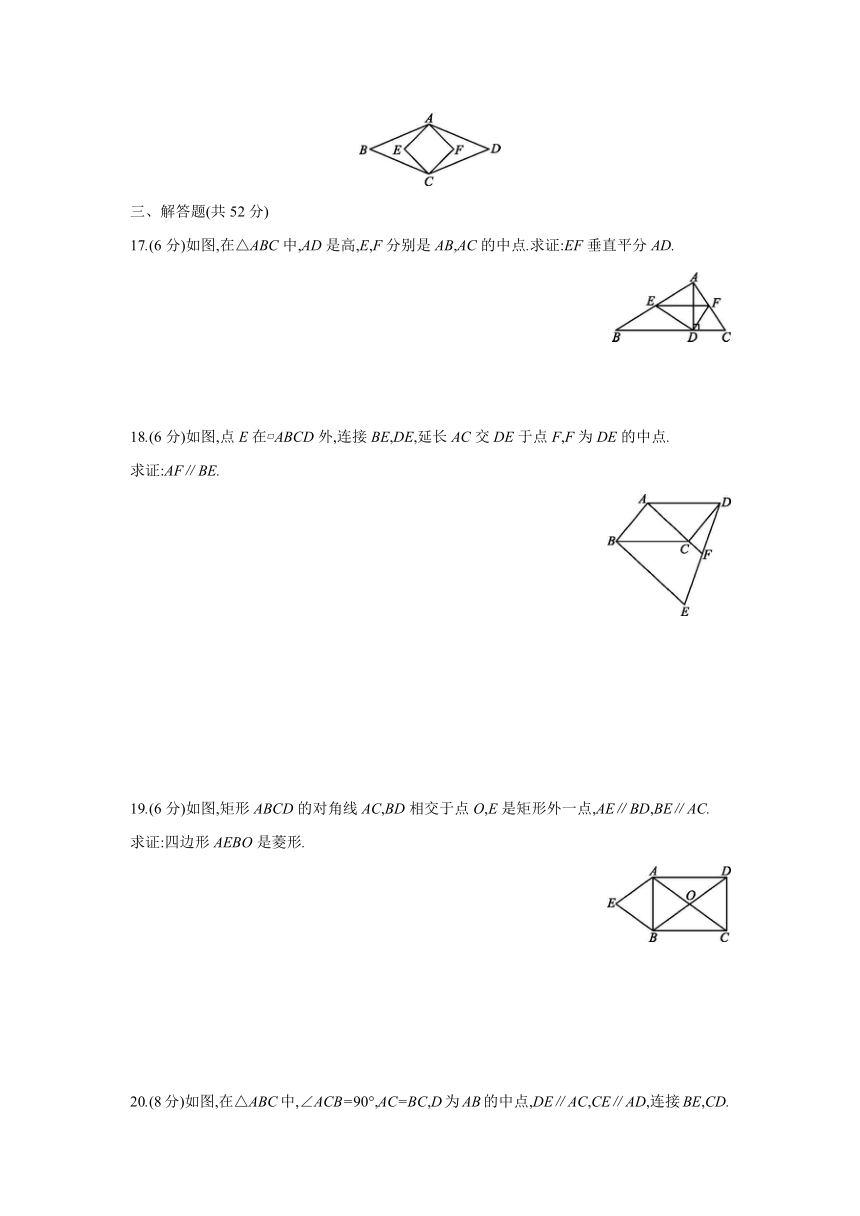
17.(6分)如图,在△ABC中,AD是高,E,F分别是AB,AC的中点.求证:EF垂直平分AD.
18.(6分)如图,点E在 ABCD外,连接BE,DE,延长AC交DE于点F,F为DE的中点.
求证:AF∥BE.
19.(6分)如图,矩形ABCD的对角线AC,BD相交于点O,E是矩形外一点,AE∥BD,BE∥AC.
求证:四边形AEBO是菱形.
20.(8分)如图,在△ABC中,∠ACB=90°,AC=BC,D为AB的中点,DE∥AC,CE∥AD,连接BE,CD.
求证:四边形CDBE是正方形.
21.(8分)如图,在四边形ABCD中,AD∥BC,BC=6厘米,AD=9厘米,点P,Q分别从点A,C同时出发,点P以1厘米/秒的速度由点A向点D运动,点Q以2厘米/秒的速度由点C向点B运动.当其中一点到达终点时,另一点也随之停止运动.
(1)经过几秒,四边形ABQP是平行四边形
(2)经过几秒,直线PQ将四边形ABCD截出一个平行四边形
22.(8分)如图,在菱形ABCD中,对角线AC,BD相交于点O,过点A作AE⊥BC于点E,将△ABE沿BC方向平移,使点B落到点C处,点E落到点F处.
(1)求证:四边形AEFD是矩形;
(2)若BD=4,DF=4,求AC的长.
23.(10分)如图,已知正方形ABCD,点P在对角线AC上,过点P作PE⊥AC交边BC于点E(点E不与点B,C重合),延长BC至点F,使得CF=BE,连接DF,PD,PF.
(1)求证:△EFP≌△CDP;
(2)若∠DFC=60°,求∠APD的度数;
(3)若O是△CDP内的一点,且DO平分∠CDP,CO平分∠PCD,请直接写出∠COD的取值范围.
答案
1.C 2.D
3.B ∵四边形ABCD是平行四边形,
∴∠A+∠B=180°,∠A=∠C.
又∵∠A=∠B-20°,∴∠C=∠A=80°.
4.D 有一组对边平行,另一组对边相等的四边形不一定是平行四边形,故选项D符合题意.
5.D ∵D,E分别为△ABC的边AC,BC的中点,
∴DE是△ABC的中位线,
∴DE∥AB,且DE=AB,
∴∠CDE=∠A,∠ADE+∠A=180°,AB=2DE.
又∵∠A=60°,DE=6,
∴∠CDE=60°,∠ADE=120°,AB=12.
由于AC的长不确定,因此DC的长不确定.故选D.
6.B ∵AB=AC=8,AD是△ABC的角平分线,
∴AD⊥BC,即∠ADC=90°.
∵BE是△ABC的中线,∴AE=CE,
∴DE=AC=×8=4.
7.C
8.B ∵D'是BC的中点,∴D'C=BC=4.
由折叠的性质知DF=D'F.
设CF=x,则D'F=DF=6-x.
在Rt△CFD'中,根据勾股定理,得D'F2=CF2+D'C2,
即(6-x)2=x2+42,解得x=,∴CF=.
9.D
10.B 连接AC,CF,则∠ACF=90°.由勾股定理知AC=,CF=3,∴AF=2.
∵H是AF的中点,∴CH=AF=.故选B.
11.3 设平行线AD,BC之间的距离为h,则有S ABCD=BC·h=6,
∴S△EBC=BC·h=3,即图中阴影部分的面积为3.
12.(6,3) ∵四边形OABC是平行四边形,
∴OA=BC,OA∥BC.
∵A(5,0),∴BC=OA=5.
∵C(1,3),∴B(6,3).
13.120° 由题意,得∠ADB=30°.
因为四边形ABCD是菱形,所以AB=AD,
所以∠ABD=∠ADB=30°,所以∠A=120°.
14.(2)两组对边分别相等的四边形是平行四边形
(3)有一个角是直角的平行四边形是矩形
15.4 如图,连接CE.
∵BD是正方形ABCD的对角线,
∴∠BCD=90°,∠ABE=∠CBE=45°,AB=CB.
又∵BE=BE,∴△ABE≌△CBE(SAS),
∴AE=CE.
∵EF⊥BC,EG⊥CD,
∴∠EGC=∠CFE=90°,
∴∠EGC=∠CFE=∠BCD=90°,
∴四边形EFCG是矩形,∴AE=CE=FG=4.
16.13 连接AC,BD.
∵正方形AECF的面积为50 cm2,
∴AE= cm=5 cm,
易得对角线AC=AE=10 cm.
∵菱形ABCD的面积为120 cm2,
∴AC·BD=120,
∴BD==24(cm),
∴菱形的边长AB==13(cm).
17.证明:∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
又E,F分别是AB,AC的中点,
∴DE=AB=AE,DF=AC=AF,
∴EF垂直平分AD.
18.证明:如图,连接BD交AC于点O.
∵四边形ABCD是平行四边形,
∴O是BD的中点.
又∵F为DE的中点,
∴OF是△DBE的中位线,
∴OF∥BE,即AF∥BE.
19.证明:∵AE∥BD,BE∥AC,
∴四边形AEBO是平行四边形.
∵四边形ABCD是矩形,
∴AC=BD,OA=OC,OB=OD,
∴OA=OB,∴四边形AEBO是菱形.
20.证明:∵DE∥AC,CE∥AD,
∴四边形ADEC是平行四边形,
∴DE=AC,CE=AD.
∵D为AB的中点,
∴AD=DB,∴CE=DB.
又∵CE∥DB,
∴四边形CDBE是平行四边形.
∵AC=BC,∴BC=DE,
∴平行四边形CDBE是矩形.
∵∠ACB=90°,AD=DB,∴CD=AD=DB,
∴矩形CDBE是正方形.
21.解:(1)设经过t秒,四边形ABQP是平行四边形.
根据题意,得AP=t厘米,CQ=2t厘米,则BQ=(6-2t)厘米.
∵AD∥BC,
∴当AP=BQ时,四边形ABQP是平行四边形,
∴t=6-2t,解得t=2,
即经过2秒,四边形ABQP是平行四边形.
(2)由(1)知,经过2秒,四边形ABQP是平行四边形.
设经过x秒,直线PQ将四边形ABCD截出的另一个四边形DCQP是平行四边形.
根据题意,得AP=x厘米,CQ=2x厘米,
则PD=(9-x)厘米.
∵AD∥BC,
∴当CQ=PD时,四边形DCQP是平行四边形,
∴2x=9-x,解得x=3.
综上,经过2秒或3秒,直线PQ将四边形ABCD截出一个平行四边形.
22.解:(1)证明:由平移的性质得AE∥DF,AE=DF,
∴四边形AEFD是平行四边形.
∵AE⊥BC,∴∠AEF=90°,
∴平行四边形AEFD是矩形.
(2)由(1)得四边形AEFD是矩形,
∴∠DFE=90°,
∴BF===8.
∵四边形ABCD是菱形,
∴OA=OC,OB=OD=BD=2,AC⊥BD,AB=BC=CD.
设AB=BC=CD=x,则CF=8-x.
在Rt△CDF中,由勾股定理,得(8-x)2+42=x2,
解得x=5,∴AB=5.
在Rt△AOB中,由勾股定理,得OA===,
∴AC=2OA=2.
23.解:(1)证明:∵四边形ABCD是正方形,AC是对角线,
∴∠ACB=∠ACD=45°,BC=CD.
∵PE⊥AC,
∴∠EPC=90°,
∴∠PEC=∠PCE=45°,∴PE=PC.
∵BE=CF,
∴EF=EC+CF=EC+BE=BC=CD.
又∵∠FEP=∠DCP=45°,
∴△EFP≌△CDP.
(2)∵四边形ABCD是正方形,
∴∠DCF=∠BCD=∠ADC=90°,∠DAC=45°.
又∵∠DFC=60°,
∴∠CDF=30°.
∵△EFP≌△CDP,
∴PF=PD,∠EPF=∠CPD,
∴∠DPF=∠EPC=90°,
∴∠PDF=∠PFD=45°,
∴∠PDC=∠PDF-∠CDF=45°-30°=15°,
∴∠ADP=90°-∠PDC=90°-15°=75°.
又∵∠DAC=45°,∴∠APD=60°.
(3)135°<∠COD<157.5°.
[测试范围:平行四边形 时间:90分钟 分值:100分]
一、选择题(每小题3分,共30分)
1.如图,直线a∥b,点A,C在直线a上,点B,D在直线b上,则直线a,b之间的距离是 ( )
A.线段AB的长度 B.线段AB
C.线段CD的长度 D.线段CD
2.如图所示的矩形是轴对称图形,对称轴可能是 ( )
A.直线l1 B.直线l2 C.直线l3 D.直线l4
3.在 ABCD中,∠A比∠B小20°,则∠C的度数为 ( )
A.60° B.80° C.100° D.120°
4.如图,在四边形ABCD中,对角线AC与BD相交于点O,下列条件中不能判定四边形ABCD是平行四边形的是 ( )
A.OA=OC,OB=OD B.AB∥CD,AD∥CB
C.AB=CD,AD=CB D.AB∥CD,AD=CB
5.如图,D,E分别为△ABC的边AC,BC的中点,∠A=60°,DE=6,则下列判断错误的是 ( )
A.∠ADE=120° B.AB=12 C.∠CDE=60° D.DC=6
6.如图,在△ABC中,AB=AC=8,AD是角平分线,BE是中线,则DE的长为 ( )
A.3 B.4 C.5 D.6
7.如图,在菱形ABCD中,点M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( )
A.28° B.52° C.62° D.72°
8.如图,将矩形纸片ABCD沿EF折叠,使点D与BC边的中点D'重合.若BC=8,CD=6,则CF的长为 ( )
A.2 B. C.2或 D.
9.学习了正方形之后,王老师提出问题:要判定一个四边形是正方形,有哪些思路 甲同学说:先判定四边形是菱形,再确定这个菱形有一个角是直角;乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等;丙同学说:判定四边形的对角线相等,并且互相垂直平分;丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等.上述四名同学的说法中,正确的是 ( )
A.甲、乙 B.甲、丙
C.乙、丙、丁 D.甲、乙、丙、丁
10.如图,在正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是 ( )
A.2.5 B. C. D.2
二、填空题(每小题3分,共18分)
11.如图,E为 ABCD的边AD上任意一点, ABCD的面积为6,则图中阴影部分的面积为 .
12.如图,将平行四边形OABC放置在平面直角坐标系xOy中,O为坐标原点.若点C的坐标是(1,3),点A的坐标是(5,0),则点B的坐标是 .
13.如图,E是菱形ABCD对角线BD延长线上一点,∠ADE=150°,则∠A的度数为 .
14.如图所示,工人师傅做一个矩形铝合金窗框分下面三个步骤进行:
(1)先截出两对符合规格的铝合金窗料(如图①所示),使AB=CD,EF=GH.
(2)摆放成如图②所示的四边形,则这时窗框的形状是平行四边形,它的依据是 .
(3)将直尺紧靠窗框的一个角(如图③),调整窗框的边框,当直角尺的两条直角边与窗框无缝隙时(如图④),说明窗框合格,这时窗框是矩形,它的依据是 .
15.如图,E是正方形ABCD的对角线BD上一点,EF⊥BC,EG⊥CD,垂足分别是F,G,连接FG,AE,FG=4,则AE= .
16.如图,菱形ABCD的面积为120 cm2,正方形AECF的面积为50 cm2,则菱形的边长为 cm.
三、解答题(共52分)
17.(6分)如图,在△ABC中,AD是高,E,F分别是AB,AC的中点.求证:EF垂直平分AD.
18.(6分)如图,点E在 ABCD外,连接BE,DE,延长AC交DE于点F,F为DE的中点.
求证:AF∥BE.
19.(6分)如图,矩形ABCD的对角线AC,BD相交于点O,E是矩形外一点,AE∥BD,BE∥AC.
求证:四边形AEBO是菱形.
20.(8分)如图,在△ABC中,∠ACB=90°,AC=BC,D为AB的中点,DE∥AC,CE∥AD,连接BE,CD.
求证:四边形CDBE是正方形.
21.(8分)如图,在四边形ABCD中,AD∥BC,BC=6厘米,AD=9厘米,点P,Q分别从点A,C同时出发,点P以1厘米/秒的速度由点A向点D运动,点Q以2厘米/秒的速度由点C向点B运动.当其中一点到达终点时,另一点也随之停止运动.
(1)经过几秒,四边形ABQP是平行四边形
(2)经过几秒,直线PQ将四边形ABCD截出一个平行四边形
22.(8分)如图,在菱形ABCD中,对角线AC,BD相交于点O,过点A作AE⊥BC于点E,将△ABE沿BC方向平移,使点B落到点C处,点E落到点F处.
(1)求证:四边形AEFD是矩形;
(2)若BD=4,DF=4,求AC的长.
23.(10分)如图,已知正方形ABCD,点P在对角线AC上,过点P作PE⊥AC交边BC于点E(点E不与点B,C重合),延长BC至点F,使得CF=BE,连接DF,PD,PF.
(1)求证:△EFP≌△CDP;
(2)若∠DFC=60°,求∠APD的度数;
(3)若O是△CDP内的一点,且DO平分∠CDP,CO平分∠PCD,请直接写出∠COD的取值范围.
答案
1.C 2.D
3.B ∵四边形ABCD是平行四边形,
∴∠A+∠B=180°,∠A=∠C.
又∵∠A=∠B-20°,∴∠C=∠A=80°.
4.D 有一组对边平行,另一组对边相等的四边形不一定是平行四边形,故选项D符合题意.
5.D ∵D,E分别为△ABC的边AC,BC的中点,
∴DE是△ABC的中位线,
∴DE∥AB,且DE=AB,
∴∠CDE=∠A,∠ADE+∠A=180°,AB=2DE.
又∵∠A=60°,DE=6,
∴∠CDE=60°,∠ADE=120°,AB=12.
由于AC的长不确定,因此DC的长不确定.故选D.
6.B ∵AB=AC=8,AD是△ABC的角平分线,
∴AD⊥BC,即∠ADC=90°.
∵BE是△ABC的中线,∴AE=CE,
∴DE=AC=×8=4.
7.C
8.B ∵D'是BC的中点,∴D'C=BC=4.
由折叠的性质知DF=D'F.
设CF=x,则D'F=DF=6-x.
在Rt△CFD'中,根据勾股定理,得D'F2=CF2+D'C2,
即(6-x)2=x2+42,解得x=,∴CF=.
9.D
10.B 连接AC,CF,则∠ACF=90°.由勾股定理知AC=,CF=3,∴AF=2.
∵H是AF的中点,∴CH=AF=.故选B.
11.3 设平行线AD,BC之间的距离为h,则有S ABCD=BC·h=6,
∴S△EBC=BC·h=3,即图中阴影部分的面积为3.
12.(6,3) ∵四边形OABC是平行四边形,
∴OA=BC,OA∥BC.
∵A(5,0),∴BC=OA=5.
∵C(1,3),∴B(6,3).
13.120° 由题意,得∠ADB=30°.
因为四边形ABCD是菱形,所以AB=AD,
所以∠ABD=∠ADB=30°,所以∠A=120°.
14.(2)两组对边分别相等的四边形是平行四边形
(3)有一个角是直角的平行四边形是矩形
15.4 如图,连接CE.
∵BD是正方形ABCD的对角线,
∴∠BCD=90°,∠ABE=∠CBE=45°,AB=CB.
又∵BE=BE,∴△ABE≌△CBE(SAS),
∴AE=CE.
∵EF⊥BC,EG⊥CD,
∴∠EGC=∠CFE=90°,
∴∠EGC=∠CFE=∠BCD=90°,
∴四边形EFCG是矩形,∴AE=CE=FG=4.
16.13 连接AC,BD.
∵正方形AECF的面积为50 cm2,
∴AE= cm=5 cm,
易得对角线AC=AE=10 cm.
∵菱形ABCD的面积为120 cm2,
∴AC·BD=120,
∴BD==24(cm),
∴菱形的边长AB==13(cm).
17.证明:∵AD是△ABC的高,
∴∠ADB=∠ADC=90°.
又E,F分别是AB,AC的中点,
∴DE=AB=AE,DF=AC=AF,
∴EF垂直平分AD.
18.证明:如图,连接BD交AC于点O.
∵四边形ABCD是平行四边形,
∴O是BD的中点.
又∵F为DE的中点,
∴OF是△DBE的中位线,
∴OF∥BE,即AF∥BE.
19.证明:∵AE∥BD,BE∥AC,
∴四边形AEBO是平行四边形.
∵四边形ABCD是矩形,
∴AC=BD,OA=OC,OB=OD,
∴OA=OB,∴四边形AEBO是菱形.
20.证明:∵DE∥AC,CE∥AD,
∴四边形ADEC是平行四边形,
∴DE=AC,CE=AD.
∵D为AB的中点,
∴AD=DB,∴CE=DB.
又∵CE∥DB,
∴四边形CDBE是平行四边形.
∵AC=BC,∴BC=DE,
∴平行四边形CDBE是矩形.
∵∠ACB=90°,AD=DB,∴CD=AD=DB,
∴矩形CDBE是正方形.
21.解:(1)设经过t秒,四边形ABQP是平行四边形.
根据题意,得AP=t厘米,CQ=2t厘米,则BQ=(6-2t)厘米.
∵AD∥BC,
∴当AP=BQ时,四边形ABQP是平行四边形,
∴t=6-2t,解得t=2,
即经过2秒,四边形ABQP是平行四边形.
(2)由(1)知,经过2秒,四边形ABQP是平行四边形.
设经过x秒,直线PQ将四边形ABCD截出的另一个四边形DCQP是平行四边形.
根据题意,得AP=x厘米,CQ=2x厘米,
则PD=(9-x)厘米.
∵AD∥BC,
∴当CQ=PD时,四边形DCQP是平行四边形,
∴2x=9-x,解得x=3.
综上,经过2秒或3秒,直线PQ将四边形ABCD截出一个平行四边形.
22.解:(1)证明:由平移的性质得AE∥DF,AE=DF,
∴四边形AEFD是平行四边形.
∵AE⊥BC,∴∠AEF=90°,
∴平行四边形AEFD是矩形.
(2)由(1)得四边形AEFD是矩形,
∴∠DFE=90°,
∴BF===8.
∵四边形ABCD是菱形,
∴OA=OC,OB=OD=BD=2,AC⊥BD,AB=BC=CD.
设AB=BC=CD=x,则CF=8-x.
在Rt△CDF中,由勾股定理,得(8-x)2+42=x2,
解得x=5,∴AB=5.
在Rt△AOB中,由勾股定理,得OA===,
∴AC=2OA=2.
23.解:(1)证明:∵四边形ABCD是正方形,AC是对角线,
∴∠ACB=∠ACD=45°,BC=CD.
∵PE⊥AC,
∴∠EPC=90°,
∴∠PEC=∠PCE=45°,∴PE=PC.
∵BE=CF,
∴EF=EC+CF=EC+BE=BC=CD.
又∵∠FEP=∠DCP=45°,
∴△EFP≌△CDP.
(2)∵四边形ABCD是正方形,
∴∠DCF=∠BCD=∠ADC=90°,∠DAC=45°.
又∵∠DFC=60°,
∴∠CDF=30°.
∵△EFP≌△CDP,
∴PF=PD,∠EPF=∠CPD,
∴∠DPF=∠EPC=90°,
∴∠PDF=∠PFD=45°,
∴∠PDC=∠PDF-∠CDF=45°-30°=15°,
∴∠ADP=90°-∠PDC=90°-15°=75°.
又∵∠DAC=45°,∴∠APD=60°.
(3)135°<∠COD<157.5°.
