全国人教版数学八年级下册课课练:专题训练 以距离为函数的实际问题(word版含答案)
文档属性
| 名称 | 全国人教版数学八年级下册课课练:专题训练 以距离为函数的实际问题(word版含答案) | 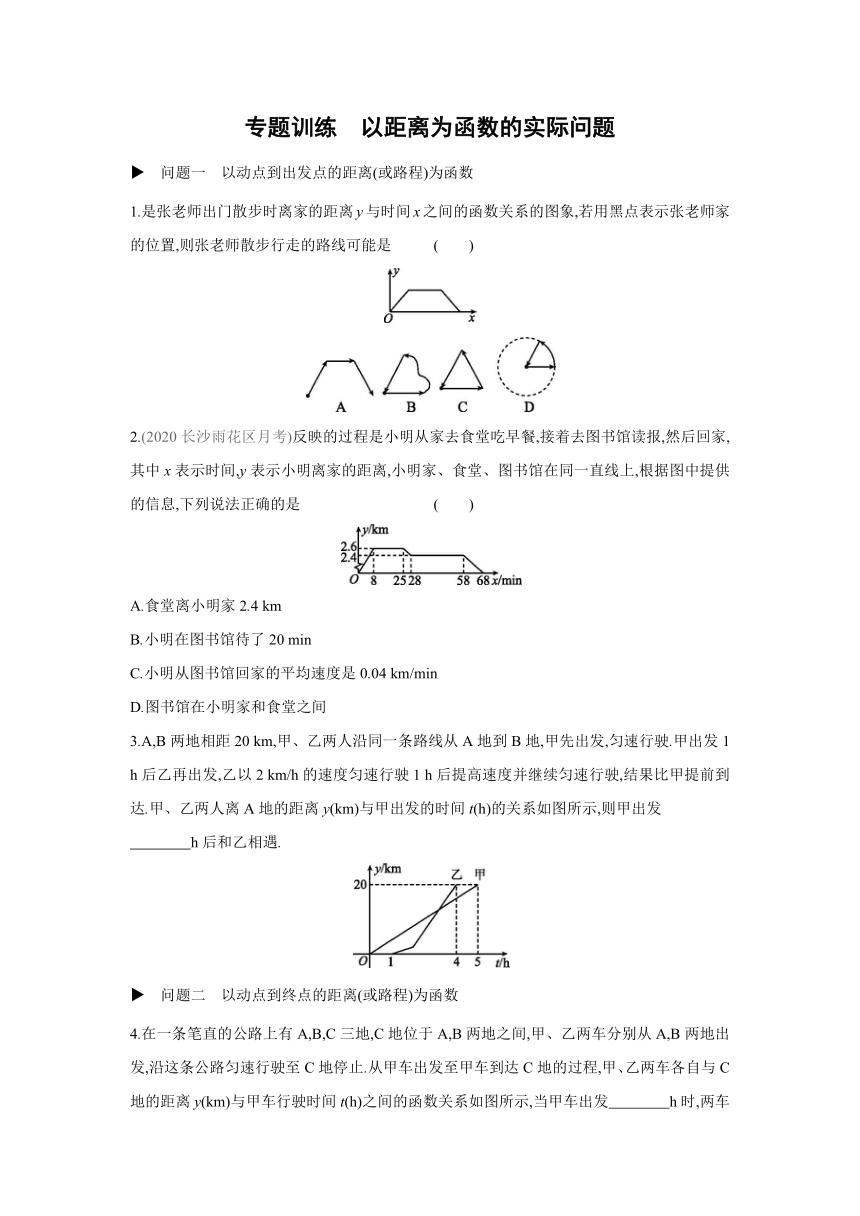 | |
| 格式 | docx | ||
| 文件大小 | 122.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 18:01:11 | ||
图片预览


文档简介
专题训练 以距离为函数的实际问题
问题一 以动点到出发点的距离(或路程)为函数
1.是张老师出门散步时离家的距离y与时间x之间的函数关系的图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是 ( )
2.(2020长沙雨花区月考)反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家,其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上,根据图中提供的信息,下列说法正确的是 ( )
A.食堂离小明家2.4 km
B.小明在图书馆待了20 min
C.小明从图书馆回家的平均速度是0.04 km/min
D.图书馆在小明家和食堂之间
3.A,B两地相距20 km,甲、乙两人沿同一条路线从A地到B地,甲先出发,匀速行驶.甲出发1 h后乙再出发,乙以2 km/h的速度匀速行驶1 h后提高速度并继续匀速行驶,结果比甲提前到达.甲、乙两人离A地的距离y(km)与甲出发的时间t(h)的关系如图所示,则甲出发
h后和乙相遇.
问题二 以动点到终点的距离(或路程)为函数
4.在一条笔直的公路上有A,B,C三地,C地位于A,B两地之间,甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止.从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示,当甲车出发 h时,两车相距350 km.
5.甲、乙两车分别从A,B两地同时出发,甲车匀速前往B地,到达B地后立即以另一速度按原路匀速返回到A地;乙车匀速前往A地.设甲、乙两车距A地的距离为y km,甲车行驶的时间为x h,y与x之间的函数图象如图所示.
(1)求甲车从A地到达B地的行驶时间;
(2)求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)求乙车到达A地时甲车距A地的路程.
问题三 以两个动点之间的距离(或路程)为函数
6.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人间的距离y(米)与甲出发的时间t(分)之间的关系如图所示,有下列结论:①甲步行的速度为60米/分;②乙走完全程用了32分钟;③乙用16分钟追上甲;④乙到达终点时,甲离终点还有300米.
其中正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
7.一天,小明从家出发匀速步行去学校上学,几分钟后,在家休假的爸爸发现小明忘带数学书,于是爸爸立即匀速跑步去追小明,爸爸追上小明后以原速原路跑回家.小明拿到书后以原速的倍快步赶往学校,并在从家出发后23分钟到校(小明被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小明从家出发去学校的步行时间x(分)之间的函数关系如图所示,则小明家到学校的路程为多少米
8.小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.中的折线表示两人之间的距离y(km)与小王的行驶时间x(h)之间的函数关系.
请你根据图象进行探究:
(1)小王和小李的速度分别是多少
(2)求线段BC所表示的y与x之间的函数解析式,并写出自变量x的取值范围.
答案
1.D 2.D
3. 由图可知,甲行驶的过程中y与t的函数解析式为y=4t.根据题意可知,乙在甲出发2 h后,开始提速,此时他距离A地1×2=2(km).设乙提速后的函数解析式为y=kt+b(k≠0),将点(2,2),(4,20)代入y=kt+b,得解得所以乙提速后的函数解析式为y=9t-16.令9t-16=4t,解得t=,即在甲出发 h后,两人相遇.
另解:由图象可知,甲的速度=20÷5=4(km/h),乙提速后的速度=(20-2)÷(4-1-1)=9(km/h).甲出发2 h后他们之间的距离=4×2-2=6(km).设甲出发x h后两人相遇,则(9-4)·(x-2)=6,解得x=,所以甲出发 h后两人相遇.
4. 由题意,得A,B两地与C地的距离均为240 km.
甲的速度为240÷4=60(km/h),乙的速度为240÷3=80(km/h).
设甲出发t h时甲、乙两车相距350 km,由题意,得60t+80(t-1)+350=240×2,
解得t=.
5.解:(1)300÷(180÷1.5)=2.5(h).
答:甲车从A地到达B地的行驶时间是2.5 h.
(2)设甲车返回时y与x之间的函数关系式为y=kx+b(k≠0),
则解得
所以甲车返回时y与x之间的函数关系式是y=-100x+550(2.5≤x≤5.5).
(3)300÷[(300-180)÷1.5]=3.75(h).
当x=3.75时,y=-100×3.75+550=175.
答:乙车到达A地时甲车距A地的路程是175 km.
6.A 由图象知,(1)甲4分钟步行了240米,所以v甲==60(米/分),可见结论①正确;(2)乙用了16-4=12(分)追上甲,可见结论③错误;(3)乙步行的速度比甲多=20(米/分),所以v乙=60+20=80(米/分),所以乙走完全程需要=30(分),可见结论②错误;(4)因为乙到达终点时,甲用了34分钟,所以甲离终点还有2400-34×60=360(米),可见结论④错误.综上所述,只有结论①正确.故选A.
7.解:设小明被爸爸追上以前的速度为a米/分,爸爸的速度为b米/分.
由题意,得解得
所以小明家到学校的路程为11×80+(23-11)××80=880+1200=2080(米).
8.解:(1)由图可得,小王的速度为30÷3=10(km/h),
小李的速度为(30-10×1)÷1=20(km/h).
答:小王和小李的速度分别是10 km/h,20 km/h.
(2)小李从乙地到甲地用的时间为30÷20=1.5(h),
当小李到达甲地时,两人之间的距离为10×1.5=15(km),
所以点C的坐标为(1.5,15).
设线段BC所表示的y与x之间的函数解析式为y=kx+b(k≠0),
则解得
故线段BC所表示的y与x之间的函数解析式是y=30x-30(1≤x≤1.5).
问题一 以动点到出发点的距离(或路程)为函数
1.是张老师出门散步时离家的距离y与时间x之间的函数关系的图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是 ( )
2.(2020长沙雨花区月考)反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家,其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上,根据图中提供的信息,下列说法正确的是 ( )
A.食堂离小明家2.4 km
B.小明在图书馆待了20 min
C.小明从图书馆回家的平均速度是0.04 km/min
D.图书馆在小明家和食堂之间
3.A,B两地相距20 km,甲、乙两人沿同一条路线从A地到B地,甲先出发,匀速行驶.甲出发1 h后乙再出发,乙以2 km/h的速度匀速行驶1 h后提高速度并继续匀速行驶,结果比甲提前到达.甲、乙两人离A地的距离y(km)与甲出发的时间t(h)的关系如图所示,则甲出发
h后和乙相遇.
问题二 以动点到终点的距离(或路程)为函数
4.在一条笔直的公路上有A,B,C三地,C地位于A,B两地之间,甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止.从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示,当甲车出发 h时,两车相距350 km.
5.甲、乙两车分别从A,B两地同时出发,甲车匀速前往B地,到达B地后立即以另一速度按原路匀速返回到A地;乙车匀速前往A地.设甲、乙两车距A地的距离为y km,甲车行驶的时间为x h,y与x之间的函数图象如图所示.
(1)求甲车从A地到达B地的行驶时间;
(2)求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)求乙车到达A地时甲车距A地的路程.
问题三 以两个动点之间的距离(或路程)为函数
6.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人间的距离y(米)与甲出发的时间t(分)之间的关系如图所示,有下列结论:①甲步行的速度为60米/分;②乙走完全程用了32分钟;③乙用16分钟追上甲;④乙到达终点时,甲离终点还有300米.
其中正确的结论有 ( )
A.1个 B.2个 C.3个 D.4个
7.一天,小明从家出发匀速步行去学校上学,几分钟后,在家休假的爸爸发现小明忘带数学书,于是爸爸立即匀速跑步去追小明,爸爸追上小明后以原速原路跑回家.小明拿到书后以原速的倍快步赶往学校,并在从家出发后23分钟到校(小明被爸爸追上时交流时间忽略不计).两人之间相距的路程y(米)与小明从家出发去学校的步行时间x(分)之间的函数关系如图所示,则小明家到学校的路程为多少米
8.小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.中的折线表示两人之间的距离y(km)与小王的行驶时间x(h)之间的函数关系.
请你根据图象进行探究:
(1)小王和小李的速度分别是多少
(2)求线段BC所表示的y与x之间的函数解析式,并写出自变量x的取值范围.
答案
1.D 2.D
3. 由图可知,甲行驶的过程中y与t的函数解析式为y=4t.根据题意可知,乙在甲出发2 h后,开始提速,此时他距离A地1×2=2(km).设乙提速后的函数解析式为y=kt+b(k≠0),将点(2,2),(4,20)代入y=kt+b,得解得所以乙提速后的函数解析式为y=9t-16.令9t-16=4t,解得t=,即在甲出发 h后,两人相遇.
另解:由图象可知,甲的速度=20÷5=4(km/h),乙提速后的速度=(20-2)÷(4-1-1)=9(km/h).甲出发2 h后他们之间的距离=4×2-2=6(km).设甲出发x h后两人相遇,则(9-4)·(x-2)=6,解得x=,所以甲出发 h后两人相遇.
4. 由题意,得A,B两地与C地的距离均为240 km.
甲的速度为240÷4=60(km/h),乙的速度为240÷3=80(km/h).
设甲出发t h时甲、乙两车相距350 km,由题意,得60t+80(t-1)+350=240×2,
解得t=.
5.解:(1)300÷(180÷1.5)=2.5(h).
答:甲车从A地到达B地的行驶时间是2.5 h.
(2)设甲车返回时y与x之间的函数关系式为y=kx+b(k≠0),
则解得
所以甲车返回时y与x之间的函数关系式是y=-100x+550(2.5≤x≤5.5).
(3)300÷[(300-180)÷1.5]=3.75(h).
当x=3.75时,y=-100×3.75+550=175.
答:乙车到达A地时甲车距A地的路程是175 km.
6.A 由图象知,(1)甲4分钟步行了240米,所以v甲==60(米/分),可见结论①正确;(2)乙用了16-4=12(分)追上甲,可见结论③错误;(3)乙步行的速度比甲多=20(米/分),所以v乙=60+20=80(米/分),所以乙走完全程需要=30(分),可见结论②错误;(4)因为乙到达终点时,甲用了34分钟,所以甲离终点还有2400-34×60=360(米),可见结论④错误.综上所述,只有结论①正确.故选A.
7.解:设小明被爸爸追上以前的速度为a米/分,爸爸的速度为b米/分.
由题意,得解得
所以小明家到学校的路程为11×80+(23-11)××80=880+1200=2080(米).
8.解:(1)由图可得,小王的速度为30÷3=10(km/h),
小李的速度为(30-10×1)÷1=20(km/h).
答:小王和小李的速度分别是10 km/h,20 km/h.
(2)小李从乙地到甲地用的时间为30÷20=1.5(h),
当小李到达甲地时,两人之间的距离为10×1.5=15(km),
所以点C的坐标为(1.5,15).
设线段BC所表示的y与x之间的函数解析式为y=kx+b(k≠0),
则解得
故线段BC所表示的y与x之间的函数解析式是y=30x-30(1≤x≤1.5).
