北师大版八年级数学上册 3.2平面直角坐标系(第3课时) 教案
文档属性
| 名称 | 北师大版八年级数学上册 3.2平面直角坐标系(第3课时) 教案 |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 18:02:15 | ||
图片预览

文档简介
第三章 位置与坐标
2 平面直角坐标系
第3课时 建立适当的平面直角坐标系
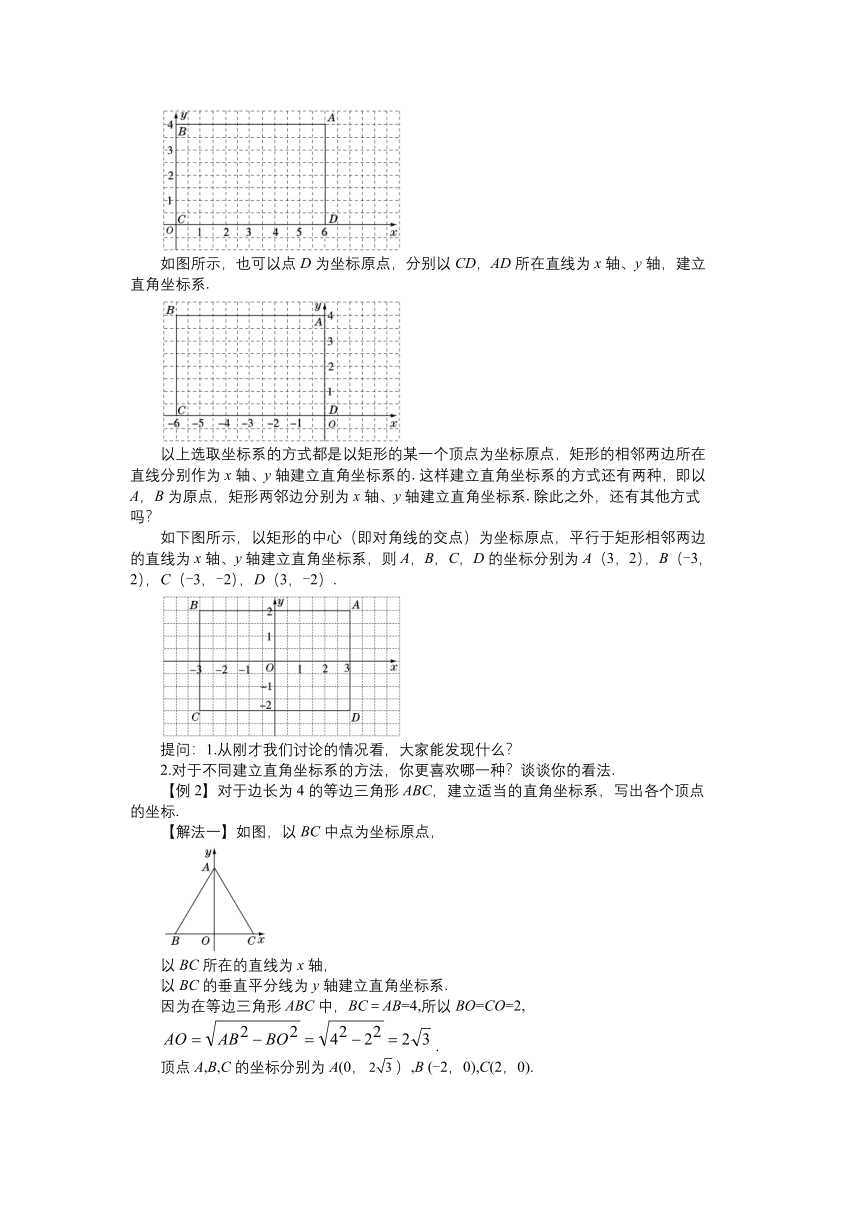
教学目标 1.让学生自主建立平面直角坐标系,从中学会合理地建立平面直角坐标系,并在坐标系中写出点的坐标. 2.通过平面直角坐标系的建立过程,体会数形结合的思想,感受点与坐标的对应关系. 教学重难点 重点:根据已知条件建立恰当的平面直角坐标系并在坐标系中写出点的坐标. 难点:根据已知条件建立恰当的平面直角坐标系. 教学过程 导入新课 有一次,小明爸爸的汽车修理厂缺少了一种如图所示的配件,小明的爸爸托在外地出差的小明的姑父购买,他用电话和小明的姑父联系,可是不管他怎么描述配件的形状和大小,小明的姑父总是弄不明白,急得小明的爸爸直跺脚.在一旁的小明接过爸爸的电话后,只描述了10个点的坐标和一个具体的单位长度,就解决了该问题.你能解释一下,小明是怎样解决这个问题的吗 探究新知 一、知识回顾 1.四个象限的点的符号特点分别是:第一象限( );第二象限( );第三象限( );第四象限( ). 2.x轴上点的( )为0;y轴上点的( )为0;原点的横纵坐标都为0,原点既在x轴上,又在y轴上. 3.平行于x轴的直线上的所有点的( )相同; 平行于y轴的直线上的所有点的( )相同. 二、新知探究 【探究1】建立平面直角坐标系,描述图形. 【例1】如图,矩形ABCD的长与宽分别是6,4,建立适当的直角坐标系,并写出各个顶点的坐标. 在没有直角坐标系的情况下不能写出各个顶点的坐标,所以应先建立直角坐标系,那么应如何选取直角坐标系呢?请大家思考. 【解】如图所示,以点C为坐标原点,分别以CD,CB所在直线为x轴、y轴,建立直角坐标系. 由CD的长为6,CB的长为4,可得A,B,C,D的坐标分别为A(6,4),B(0,4),C(0,0),D(6,0). 如图所示,也可以点D为坐标原点,分别以CD,AD所在直线为x轴、y轴,建立直角坐标系. 以上选取坐标系的方式都是以矩形的某一个顶点为坐标原点,矩形的相邻两边所在直线分别作为x轴、y轴建立直角坐标系的.这样建立直角坐标系的方式还有两种,即以A,B为原点,矩形两邻边分别为x轴、y轴建立直角坐标系.除此之外,还有其他方式吗? 如下图所示,以矩形的中心(即对角线的交点)为坐标原点,平行于矩形相邻两边的直线为x轴、y轴建立直角坐标系,则A,B,C,D的坐标分别为A(3,2),B(-3,2),C(-3,-2),D(3,-2). 提问:1.从刚才我们讨论的情况看,大家能发现什么? 2.对于不同建立直角坐标系的方法,你更喜欢哪一种?谈谈你的看法. 【例2】对于边长为4的等边三角形ABC,建立适当的直角坐标系,写出各个顶点的坐标. 【解法一】如图,以BC中点为坐标原点, 以BC所在的直线为x轴, 以BC的垂直平分线为y轴建立直角坐标系. 因为在等边三角形ABC中,BC=AB=4,所以BO=CO=2, . 顶点A,B,C的坐标分别为A(0,),B (-2,0),C(2,0). 【解法二】如图. 思考:除了上面的直角坐标系的选取外,是否还有其他的选取方法? 【探究2】根据点的坐标复原坐标系. 【例3】在一次“寻宝”游戏中,寻宝人已经找到了坐标为A(3,2)和B(3,-2)的两个点,并且知道藏宝地点的坐标为(4,4),除此外不知道其他信息.如何确定直角坐标系找到宝藏? 【解】如图,连接AB,作线段AB的垂直平分线,记为x轴,以AB的中点为起点,以AB长度的四分之一为一个单位长度,从AB与x轴的交点向左3个单位长度为坐标原点O,过原点O作x轴的垂线记为y轴,建立平面直角坐标系,找到(4,4)即可. 教学处理:(1)让学生分组讨论如何找到宝藏;(2)让每组选一名代表发言,阐述本组讨论的结果;(3)师生共同完成“寻宝”. 三、练习巩固,拓展提高 1.如图,在一次军棋比赛中,如果团长所在位置的坐标为(2,-5),司令所在位置的坐标为(4,-2),那么工兵所在位置的坐标为________. 解析:团长所在位置的坐标为(2,-5),司令所在位置的坐标为(4,-2),由此确定原点的位置,从而得出工兵所在位置的坐标为(1,-2). 答案:(1,-2) 2.某地为了发展城市群,在现有的四个中小城市A,B,C,D附近新建机场E,试建立适当的直角坐标系,并写出各点的坐标. 解:答案不唯一,可以以点A为坐标原点,建立平面直角坐标系,图略. 课堂练习 1.如图所示的是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为( ) A.(2,3),(3,2) B.(3,2),(2,3) C.(2,3),(-3,2) D.(3,2),(-2,3) 2.如图所示,若“帅”位于点(1,-2)上,“相”位于点(3,-2)上,则“炮”位于点________. 3.如图所示,若点E的坐标为(-2,1),点F的坐标为(1,-1),则点G的坐标为 . 4.如图所示,正方形ABCD的边长为10,连接各边的中点E,F,G,H得到正方形EFGH,请你建立适当的坐标系,分别写出A,B,C,D,E,F,G,H的坐标. 参考答案 1.D 2.(-2,1) 3.(1,2) 4.解:答案不唯一,如:以EG所在直线为x轴,以FH所在直线为y轴,建立如图所示的坐标系,则A(-5,-5),B(5,-5),C(5,5),D(-5,5),E(-5,0), F(0,-5),G(5,0),H(0,5). 课堂小结 同一个图形建立适当的平面直角坐标系的方法不唯一,要选用点的坐标易求的方法建系. 布置作业 A类:习题3.4. B类:完成A类同时,补充: 在平面直角坐标系中,点A的坐标是(-3,4),点B的坐标是(-1,-2),点O为坐标原点,求△AOB的面积. 板书设计 2 平面直角坐标系 第3课时 建立适当的平面直角坐标系 1.利用平面直角坐标系确定位置. 2.建立合适的平面直角坐标系解决问题.
2 平面直角坐标系
第3课时 建立适当的平面直角坐标系
教学目标 1.让学生自主建立平面直角坐标系,从中学会合理地建立平面直角坐标系,并在坐标系中写出点的坐标. 2.通过平面直角坐标系的建立过程,体会数形结合的思想,感受点与坐标的对应关系. 教学重难点 重点:根据已知条件建立恰当的平面直角坐标系并在坐标系中写出点的坐标. 难点:根据已知条件建立恰当的平面直角坐标系. 教学过程 导入新课 有一次,小明爸爸的汽车修理厂缺少了一种如图所示的配件,小明的爸爸托在外地出差的小明的姑父购买,他用电话和小明的姑父联系,可是不管他怎么描述配件的形状和大小,小明的姑父总是弄不明白,急得小明的爸爸直跺脚.在一旁的小明接过爸爸的电话后,只描述了10个点的坐标和一个具体的单位长度,就解决了该问题.你能解释一下,小明是怎样解决这个问题的吗 探究新知 一、知识回顾 1.四个象限的点的符号特点分别是:第一象限( );第二象限( );第三象限( );第四象限( ). 2.x轴上点的( )为0;y轴上点的( )为0;原点的横纵坐标都为0,原点既在x轴上,又在y轴上. 3.平行于x轴的直线上的所有点的( )相同; 平行于y轴的直线上的所有点的( )相同. 二、新知探究 【探究1】建立平面直角坐标系,描述图形. 【例1】如图,矩形ABCD的长与宽分别是6,4,建立适当的直角坐标系,并写出各个顶点的坐标. 在没有直角坐标系的情况下不能写出各个顶点的坐标,所以应先建立直角坐标系,那么应如何选取直角坐标系呢?请大家思考. 【解】如图所示,以点C为坐标原点,分别以CD,CB所在直线为x轴、y轴,建立直角坐标系. 由CD的长为6,CB的长为4,可得A,B,C,D的坐标分别为A(6,4),B(0,4),C(0,0),D(6,0). 如图所示,也可以点D为坐标原点,分别以CD,AD所在直线为x轴、y轴,建立直角坐标系. 以上选取坐标系的方式都是以矩形的某一个顶点为坐标原点,矩形的相邻两边所在直线分别作为x轴、y轴建立直角坐标系的.这样建立直角坐标系的方式还有两种,即以A,B为原点,矩形两邻边分别为x轴、y轴建立直角坐标系.除此之外,还有其他方式吗? 如下图所示,以矩形的中心(即对角线的交点)为坐标原点,平行于矩形相邻两边的直线为x轴、y轴建立直角坐标系,则A,B,C,D的坐标分别为A(3,2),B(-3,2),C(-3,-2),D(3,-2). 提问:1.从刚才我们讨论的情况看,大家能发现什么? 2.对于不同建立直角坐标系的方法,你更喜欢哪一种?谈谈你的看法. 【例2】对于边长为4的等边三角形ABC,建立适当的直角坐标系,写出各个顶点的坐标. 【解法一】如图,以BC中点为坐标原点, 以BC所在的直线为x轴, 以BC的垂直平分线为y轴建立直角坐标系. 因为在等边三角形ABC中,BC=AB=4,所以BO=CO=2, . 顶点A,B,C的坐标分别为A(0,),B (-2,0),C(2,0). 【解法二】如图. 思考:除了上面的直角坐标系的选取外,是否还有其他的选取方法? 【探究2】根据点的坐标复原坐标系. 【例3】在一次“寻宝”游戏中,寻宝人已经找到了坐标为A(3,2)和B(3,-2)的两个点,并且知道藏宝地点的坐标为(4,4),除此外不知道其他信息.如何确定直角坐标系找到宝藏? 【解】如图,连接AB,作线段AB的垂直平分线,记为x轴,以AB的中点为起点,以AB长度的四分之一为一个单位长度,从AB与x轴的交点向左3个单位长度为坐标原点O,过原点O作x轴的垂线记为y轴,建立平面直角坐标系,找到(4,4)即可. 教学处理:(1)让学生分组讨论如何找到宝藏;(2)让每组选一名代表发言,阐述本组讨论的结果;(3)师生共同完成“寻宝”. 三、练习巩固,拓展提高 1.如图,在一次军棋比赛中,如果团长所在位置的坐标为(2,-5),司令所在位置的坐标为(4,-2),那么工兵所在位置的坐标为________. 解析:团长所在位置的坐标为(2,-5),司令所在位置的坐标为(4,-2),由此确定原点的位置,从而得出工兵所在位置的坐标为(1,-2). 答案:(1,-2) 2.某地为了发展城市群,在现有的四个中小城市A,B,C,D附近新建机场E,试建立适当的直角坐标系,并写出各点的坐标. 解:答案不唯一,可以以点A为坐标原点,建立平面直角坐标系,图略. 课堂练习 1.如图所示的是A,B,C,D四位同学的家所在位置,若以A同学家的位置为坐标原点建立平面直角坐标系,那么C同学家的位置的坐标为(1,5),则B,D两同学家的坐标分别为( ) A.(2,3),(3,2) B.(3,2),(2,3) C.(2,3),(-3,2) D.(3,2),(-2,3) 2.如图所示,若“帅”位于点(1,-2)上,“相”位于点(3,-2)上,则“炮”位于点________. 3.如图所示,若点E的坐标为(-2,1),点F的坐标为(1,-1),则点G的坐标为 . 4.如图所示,正方形ABCD的边长为10,连接各边的中点E,F,G,H得到正方形EFGH,请你建立适当的坐标系,分别写出A,B,C,D,E,F,G,H的坐标. 参考答案 1.D 2.(-2,1) 3.(1,2) 4.解:答案不唯一,如:以EG所在直线为x轴,以FH所在直线为y轴,建立如图所示的坐标系,则A(-5,-5),B(5,-5),C(5,5),D(-5,5),E(-5,0), F(0,-5),G(5,0),H(0,5). 课堂小结 同一个图形建立适当的平面直角坐标系的方法不唯一,要选用点的坐标易求的方法建系. 布置作业 A类:习题3.4. B类:完成A类同时,补充: 在平面直角坐标系中,点A的坐标是(-3,4),点B的坐标是(-1,-2),点O为坐标原点,求△AOB的面积. 板书设计 2 平面直角坐标系 第3课时 建立适当的平面直角坐标系 1.利用平面直角坐标系确定位置. 2.建立合适的平面直角坐标系解决问题.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
