三角函数图象变换[下学期]
图片预览



文档简介
1
课 题:函数y=Asin(ωx+) 的图象
授课人:
教学目的:
1.探索学生合作学习的形式,培养学生合作交流的能力.
2.会用五点法画出函数y=Asinx、y=Asinωx和的图象,明确A、ω和对函数图象的影响作用;并会由y=sinx的图象得出y=Asinx、y=Asinωx和的图象。
3.理解振幅变换、周期变换和相位变换的规律;
教学重点:熟练地对y=sinx进行振幅、周期变换和相位变换.
教学难点:理解振幅变换和周期变换的规律
授课类型:新授课
课时安排:1课时
教 具:多媒体、实物投影仪
教学过程:
一、新课引入:
师:前面我们学习了正弦函数y=sinx的图象和性质,请同学画出它的草图并说出它的定义域、值域、奇偶性、周期及单调区间?
生:定义域:R,值域:[-1,1],奇函数,单增区间:,单减区间:
师:回答的很好,那么形如函数的定义域、值域、奇偶性、周期及单调区间又如何呢?
(一片茫然,没有学生回答)
师:大家别着急,今天我们就要来学习它们的图象和性质,并通过它们的图象和性质进一步来探究它们的图象与y=sinx图象会有什么样的关系.
二、分小组画图讨论
下面请请第一到第五组的同学用五点法画出以下第一组三角函数的图象,第六到第十组的同学画出以下第二组三角函数的图象,第11到第15组的同学画出以下第三组三角函数的图象,并观察每一组图象的定义域、值域、周期、单调区间及其相互之间的关系、特点,然后进行小组内讨论、交流.
第一组:
第二组:
第三组:
(教师巡视)
三、师生交流:
师:从下列第一组图1,你有什么体会?
图1
师:y=2sinx的周期是多少?请第二组同学代表回答.
生:y=2sinx的定义域:x∈R,值域:y[-2,2],周期:应该与y=sinx的一样还是
师:不错,那么呢?
生:的定义域x∈R,值域:y∈[-],周期:
师:很好,那么它们三者之间的图象有什么关系呢?
生:好象它们之间有一定的伸缩关系
师:能不能再说得具体一点吗?
生:伸缩倍数是不是与2和有关呢?
师:大家探究和分析的很好,是不是这样呢?不过别着急.下面请大家先看大屏幕几何画板的动画演示
(他们能够说出“伸缩”二字,而且发现与2和有关,只是猜想不知是否正确,此时,利用动画演示有助于验证他们的猜想)
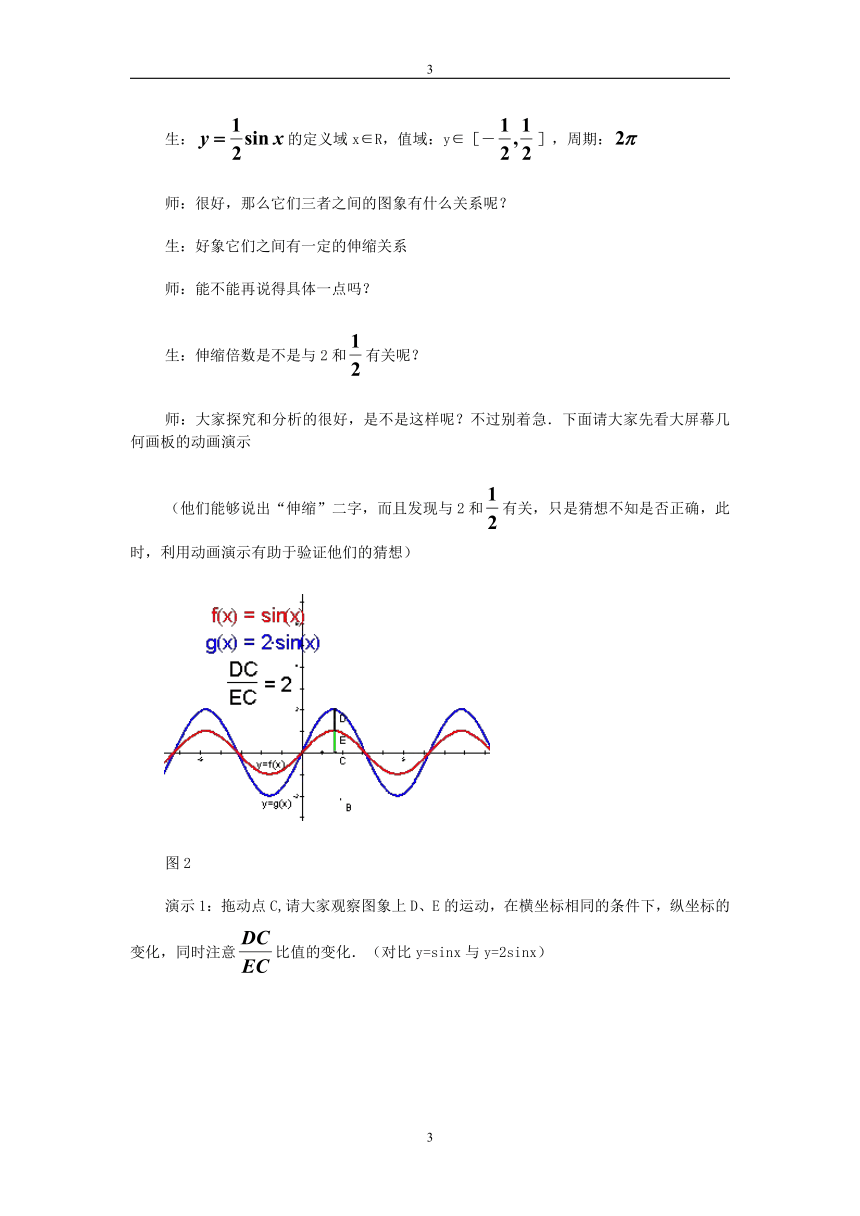
图2
演示1:拖动点C,请大家观察图象上D、E的运动,在横坐标相同的条件下,纵坐标的变化,同时注意比值的变化.(对比y=sinx与y=2sinx)
图3
演示2:拖动点B,观察图象y=sinx与y=Asinx图象,当A发生变化时,点D、E的纵坐标的变化,同时注意比值的变化.(改变A的值,整体对比y=sinx与y=Asinx的关系)
进一步引导,观察,启发:
师:通过大家的作图和我刚才的几何画板演示,你又有什么体会?
生: 函数y=1/2sinx的图象可看作把y=sinx,x∈R上所有点的纵坐标缩短到原来的 1/2倍而得(横坐标不变),函数y=2sinx图象可看作把y=sinx,x∈R上所有点的纵坐标缩短到原来的2倍而得(横坐标不变)
师:太好了,回答完全正确.
(演示进一步巩固了他们的猜想)
总结:
一般地,y=Asinx,(x∈R,A>0且)的图象可以看作把正弦曲线y=sinx上的所有点的纵坐标伸长(A>1)或缩短(0第二组:
师生交流:
师:和第一组一样,你们有什么体会?请第七组同学代表回答
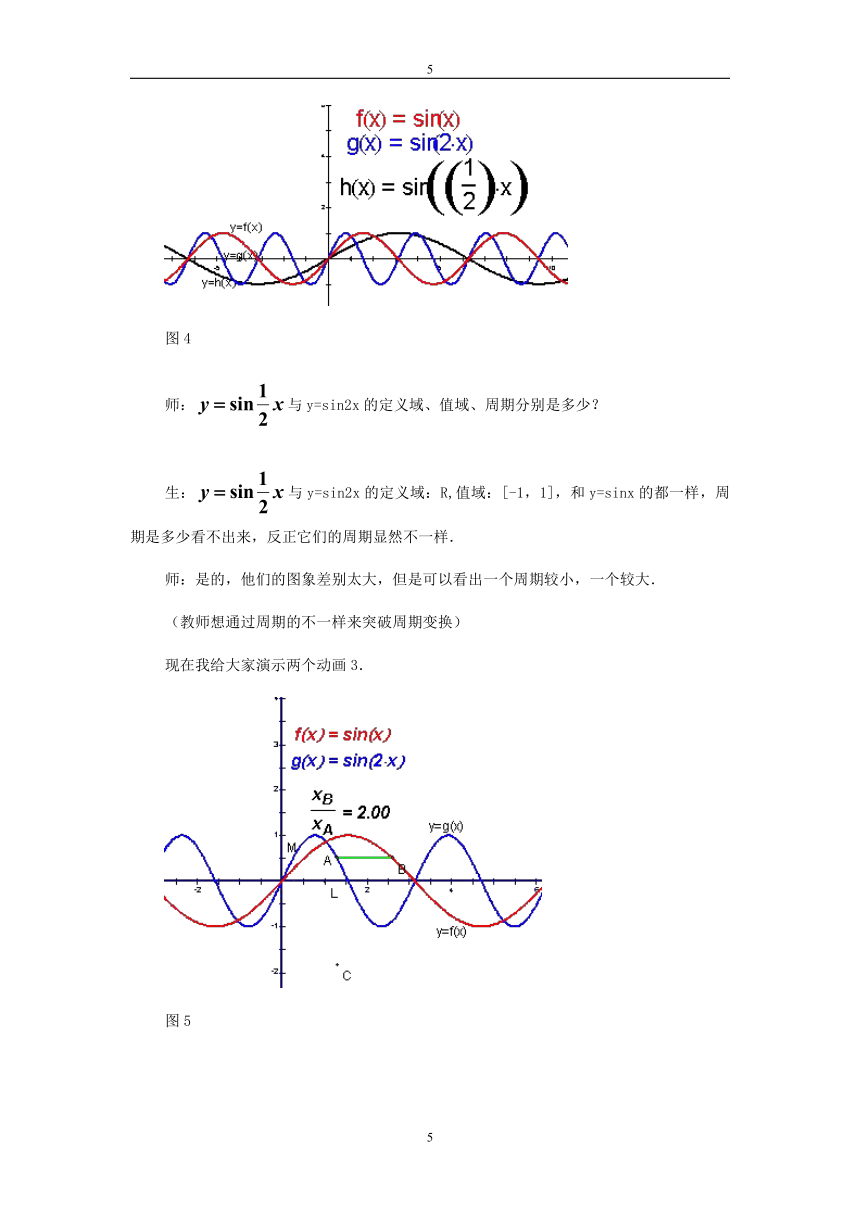
图4
师:与y=sin2x的定义域、值域、周期分别是多少?
生:与y=sin2x的定义域:R,值域:[-1,1],和y=sinx的都一样,周期是多少看不出来,反正它们的周期显然不一样.
师:是的,他们的图象差别太大,但是可以看出一个周期较小,一个较大.
(教师想通过周期的不一样来突破周期变换)
现在我给大家演示两个动画3.
图5
演示1:拖动点A (A、B,它们分别在各自的图象上)在纵坐标相同的条件下,观察A、B的横坐标的变化,以及的比值的变化.(对比y=sinx与y=sin2x的关系)
演示2:拖动点B, 改变W的值,再观察上述的变化.(改变W的值,进一步观察y=sinx与y=sinWx的图象关系)
(该环节的演示要慢,要让学生注意观察比值的不变特点)
图6
进一步引导, 观察启发:
师:通过上述你的实验、和几何画板的动画演示,你又有什么体会?
生:函数y=sin2x,x∈R的图象,可看作把y=sinx,x∈R上所有点的横坐标缩短到原来的倍(纵坐标不变)而得到的 函数y=sin,x∈R的图象,可看作把y=sinx(x∈R)上所有点的横坐标伸长到原来的2倍(纵坐标不变)而得到
(的确难得,他们能发现影响周期的量是W了,这样也为下一节课周期的教学作好准备)
师:大家已经能通过第一组的变换特点,类比的方式得到它们之间的关系,真的很不错.那么谁能把y=sinωx图象与y=sinx的图象作比较 ,说出它们之间的关系吗?
生:函数y=sinωx, x∈R (ω>0且)的图象,可看作把y=sinx所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的倍(纵坐标不变)
(鼓励学生用自己的语言来归纳,总结)
师:有进步.
总结:
一般地,函数y=sinωx, x∈R (ω>0且)的图象,可看作把正弦曲线上所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的倍(纵坐标不变).我们把这种变换简称为周期变换.
第三组:
图7
师:它们的定义域、值域、周期分别是多少?以及它们的图象关系又有如何关系?
生:定义域:x∈R,值域:y ∈[-1,1],周期:,相互间好象可以通过左右平移得到。
师:回答的十分正确.请大家看我用几何画板的动画演示4.
演示1:拖动点C,观察变化.(观察平移的单位)
演示2:拖动点B,改变B的值,观察平移的方向.(让学生去发现:从左边移动(B>0),从右边移动(B<0)
引导,观察,启发:
师:通过上述实验、和几何画板演示的结果你有什么体会?
生:函数的图象可看作把正弦曲线y=sinx上所有的点向左平行移动个单位长度而得到 .函数的图象可看作把正弦曲线y=sinx上所有点向右平行移动个单位长度而得到
师:太棒了,回答的十分正确.
教师总结:
一般地,函数y=sin(x+),x∈R(其中≠0)的图象,可以看作把正弦曲线上所有点向左(当>0时)或向右(当<0时=平行移动||个单位长度而得到 (用平移法注意讲清方向:“左加”“右减”),我们把这一变换称为相位变换
四、课堂练习:
1.(1)y=sin(x+)是由y=sinx向左平移个单位得到的.
(2)y=sin(x-)是由y=sinx向右平移个单位得到的.
(3)y=sin(2x-)是由y=sin2x向右平移个单位得到的.
(4)y=sin(x-)是由y=sin(x+)向右平移个单位得到的.
(5)y=sinx与y=3sinx的图象有什么关系?
2.若将某函数的图象向右平移以后所得到的图象的函数式是y=sin(x+),则原来的函数表达式为( )
A.y=sin(x+) B.y=sin(x+)
C.y=sin(x-) D.y=sin(x+)-
答案:A
3、为了得到函数的图象,只需将函数的图象上的每个点( )
A.横坐标伸长为原来的2倍,纵坐标不变
B. 横坐标伸长为原来的1/2倍,纵坐标不变
C. 纵坐标伸长为原来的2倍,横坐标不变
D.纵坐标伸长为原来的1/2倍,横坐标不变
4、为了得到函数的图象,只需将函数的图象上的每个点( )
A.横坐标向左平移个单位长度 B. 横坐标向右平移个单位长度
C. 横坐标向左平移个单位长度 D. 横坐标向右平移个单位长度
五、小结与思考:
今天我们学习了三种三角函数:形如图象是由y=sinx的图象怎么变换得到,我们分别把三种变换分别称为振幅变换、周期变换、相位变换.
课后思考:函数的图象怎样由y=sinx的图象变换得到。
六、作业:略
1
课 题:函数y=Asin(ωx+) 的图象
授课人:
教学目的:
1.探索学生合作学习的形式,培养学生合作交流的能力.
2.会用五点法画出函数y=Asinx、y=Asinωx和的图象,明确A、ω和对函数图象的影响作用;并会由y=sinx的图象得出y=Asinx、y=Asinωx和的图象。
3.理解振幅变换、周期变换和相位变换的规律;
教学重点:熟练地对y=sinx进行振幅、周期变换和相位变换.
教学难点:理解振幅变换和周期变换的规律
授课类型:新授课
课时安排:1课时
教 具:多媒体、实物投影仪
教学过程:
一、新课引入:
师:前面我们学习了正弦函数y=sinx的图象和性质,请同学画出它的草图并说出它的定义域、值域、奇偶性、周期及单调区间?
生:定义域:R,值域:[-1,1],奇函数,单增区间:,单减区间:
师:回答的很好,那么形如函数的定义域、值域、奇偶性、周期及单调区间又如何呢?
(一片茫然,没有学生回答)
师:大家别着急,今天我们就要来学习它们的图象和性质,并通过它们的图象和性质进一步来探究它们的图象与y=sinx图象会有什么样的关系.
二、分小组画图讨论
下面请请第一到第五组的同学用五点法画出以下第一组三角函数的图象,第六到第十组的同学画出以下第二组三角函数的图象,第11到第15组的同学画出以下第三组三角函数的图象,并观察每一组图象的定义域、值域、周期、单调区间及其相互之间的关系、特点,然后进行小组内讨论、交流.
第一组:
第二组:
第三组:
(教师巡视)
三、师生交流:
师:从下列第一组图1,你有什么体会?
图1
师:y=2sinx的周期是多少?请第二组同学代表回答.
生:y=2sinx的定义域:x∈R,值域:y[-2,2],周期:应该与y=sinx的一样还是
师:不错,那么呢?
生:的定义域x∈R,值域:y∈[-],周期:
师:很好,那么它们三者之间的图象有什么关系呢?
生:好象它们之间有一定的伸缩关系
师:能不能再说得具体一点吗?
生:伸缩倍数是不是与2和有关呢?
师:大家探究和分析的很好,是不是这样呢?不过别着急.下面请大家先看大屏幕几何画板的动画演示
(他们能够说出“伸缩”二字,而且发现与2和有关,只是猜想不知是否正确,此时,利用动画演示有助于验证他们的猜想)
图2
演示1:拖动点C,请大家观察图象上D、E的运动,在横坐标相同的条件下,纵坐标的变化,同时注意比值的变化.(对比y=sinx与y=2sinx)
图3
演示2:拖动点B,观察图象y=sinx与y=Asinx图象,当A发生变化时,点D、E的纵坐标的变化,同时注意比值的变化.(改变A的值,整体对比y=sinx与y=Asinx的关系)
进一步引导,观察,启发:
师:通过大家的作图和我刚才的几何画板演示,你又有什么体会?
生: 函数y=1/2sinx的图象可看作把y=sinx,x∈R上所有点的纵坐标缩短到原来的 1/2倍而得(横坐标不变),函数y=2sinx图象可看作把y=sinx,x∈R上所有点的纵坐标缩短到原来的2倍而得(横坐标不变)
师:太好了,回答完全正确.
(演示进一步巩固了他们的猜想)
总结:
一般地,y=Asinx,(x∈R,A>0且)的图象可以看作把正弦曲线y=sinx上的所有点的纵坐标伸长(A>1)或缩短(0
师生交流:
师:和第一组一样,你们有什么体会?请第七组同学代表回答
图4
师:与y=sin2x的定义域、值域、周期分别是多少?
生:与y=sin2x的定义域:R,值域:[-1,1],和y=sinx的都一样,周期是多少看不出来,反正它们的周期显然不一样.
师:是的,他们的图象差别太大,但是可以看出一个周期较小,一个较大.
(教师想通过周期的不一样来突破周期变换)
现在我给大家演示两个动画3.
图5
演示1:拖动点A (A、B,它们分别在各自的图象上)在纵坐标相同的条件下,观察A、B的横坐标的变化,以及的比值的变化.(对比y=sinx与y=sin2x的关系)
演示2:拖动点B, 改变W的值,再观察上述的变化.(改变W的值,进一步观察y=sinx与y=sinWx的图象关系)
(该环节的演示要慢,要让学生注意观察比值的不变特点)
图6
进一步引导, 观察启发:
师:通过上述你的实验、和几何画板的动画演示,你又有什么体会?
生:函数y=sin2x,x∈R的图象,可看作把y=sinx,x∈R上所有点的横坐标缩短到原来的倍(纵坐标不变)而得到的 函数y=sin,x∈R的图象,可看作把y=sinx(x∈R)上所有点的横坐标伸长到原来的2倍(纵坐标不变)而得到
(的确难得,他们能发现影响周期的量是W了,这样也为下一节课周期的教学作好准备)
师:大家已经能通过第一组的变换特点,类比的方式得到它们之间的关系,真的很不错.那么谁能把y=sinωx图象与y=sinx的图象作比较 ,说出它们之间的关系吗?
生:函数y=sinωx, x∈R (ω>0且)的图象,可看作把y=sinx所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的倍(纵坐标不变)
(鼓励学生用自己的语言来归纳,总结)
师:有进步.
总结:
一般地,函数y=sinωx, x∈R (ω>0且)的图象,可看作把正弦曲线上所有点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的倍(纵坐标不变).我们把这种变换简称为周期变换.
第三组:
图7
师:它们的定义域、值域、周期分别是多少?以及它们的图象关系又有如何关系?
生:定义域:x∈R,值域:y ∈[-1,1],周期:,相互间好象可以通过左右平移得到。
师:回答的十分正确.请大家看我用几何画板的动画演示4.
演示1:拖动点C,观察变化.(观察平移的单位)
演示2:拖动点B,改变B的值,观察平移的方向.(让学生去发现:从左边移动(B>0),从右边移动(B<0)
引导,观察,启发:
师:通过上述实验、和几何画板演示的结果你有什么体会?
生:函数的图象可看作把正弦曲线y=sinx上所有的点向左平行移动个单位长度而得到 .函数的图象可看作把正弦曲线y=sinx上所有点向右平行移动个单位长度而得到
师:太棒了,回答的十分正确.
教师总结:
一般地,函数y=sin(x+),x∈R(其中≠0)的图象,可以看作把正弦曲线上所有点向左(当>0时)或向右(当<0时=平行移动||个单位长度而得到 (用平移法注意讲清方向:“左加”“右减”),我们把这一变换称为相位变换
四、课堂练习:
1.(1)y=sin(x+)是由y=sinx向左平移个单位得到的.
(2)y=sin(x-)是由y=sinx向右平移个单位得到的.
(3)y=sin(2x-)是由y=sin2x向右平移个单位得到的.
(4)y=sin(x-)是由y=sin(x+)向右平移个单位得到的.
(5)y=sinx与y=3sinx的图象有什么关系?
2.若将某函数的图象向右平移以后所得到的图象的函数式是y=sin(x+),则原来的函数表达式为( )
A.y=sin(x+) B.y=sin(x+)
C.y=sin(x-) D.y=sin(x+)-
答案:A
3、为了得到函数的图象,只需将函数的图象上的每个点( )
A.横坐标伸长为原来的2倍,纵坐标不变
B. 横坐标伸长为原来的1/2倍,纵坐标不变
C. 纵坐标伸长为原来的2倍,横坐标不变
D.纵坐标伸长为原来的1/2倍,横坐标不变
4、为了得到函数的图象,只需将函数的图象上的每个点( )
A.横坐标向左平移个单位长度 B. 横坐标向右平移个单位长度
C. 横坐标向左平移个单位长度 D. 横坐标向右平移个单位长度
五、小结与思考:
今天我们学习了三种三角函数:形如图象是由y=sinx的图象怎么变换得到,我们分别把三种变换分别称为振幅变换、周期变换、相位变换.
课后思考:函数的图象怎样由y=sinx的图象变换得到。
六、作业:略
1
