11.1.2第3课时三角形的中线 课件(共18页)
文档属性
| 名称 | 11.1.2第3课时三角形的中线 课件(共18页) |  | |
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 17:06:47 | ||
图片预览


文档简介
(共18张PPT)
11.1 与三角形有关的线段
11.1.2第3课时三角形的中线
精品同步教学课件
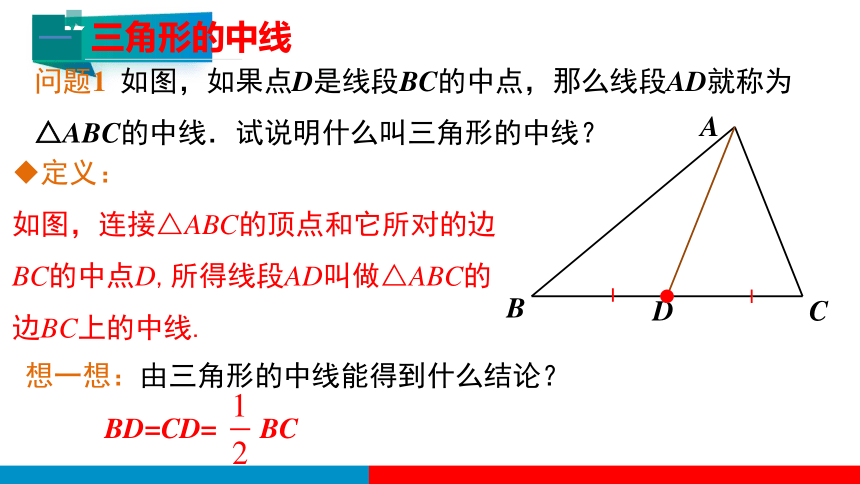
问题1 如图,如果点D是线段BC的中点,那么线段AD就称为△ABC的中线.试说明什么叫三角形的中线?
A
B
C
定义:
如图,连接△ABC的顶点和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线.
想一想:由三角形的中线能得到什么结论?
BD=CD= BC
D
三角形的中线
一
A
B
C
D
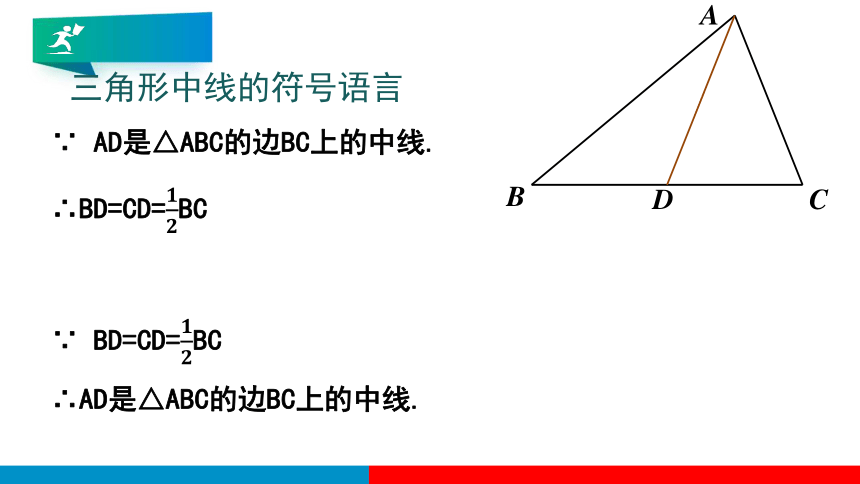
∵ AD是△ABC的边BC上的中线.
∴BD=CD=BC
三角形中线的符号语言
∵ BD=CD=BC
∴AD是△ABC的边BC上的中线.
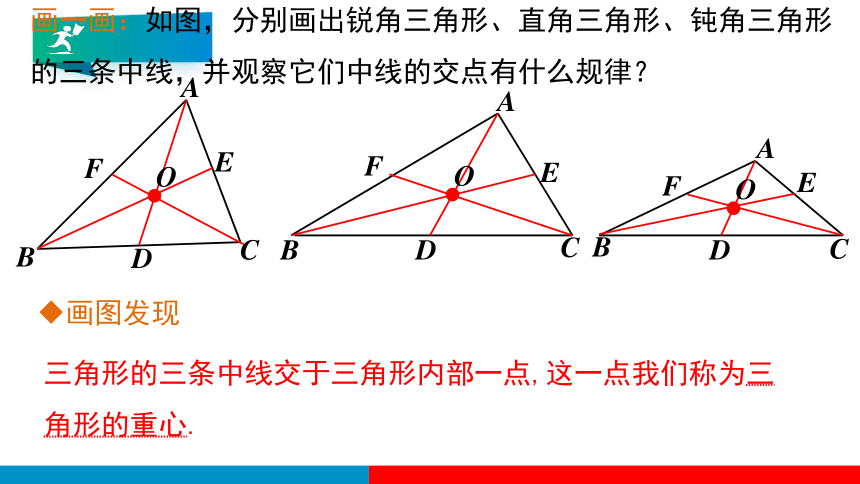
画一画:如图,分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?
画图发现
三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心.
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
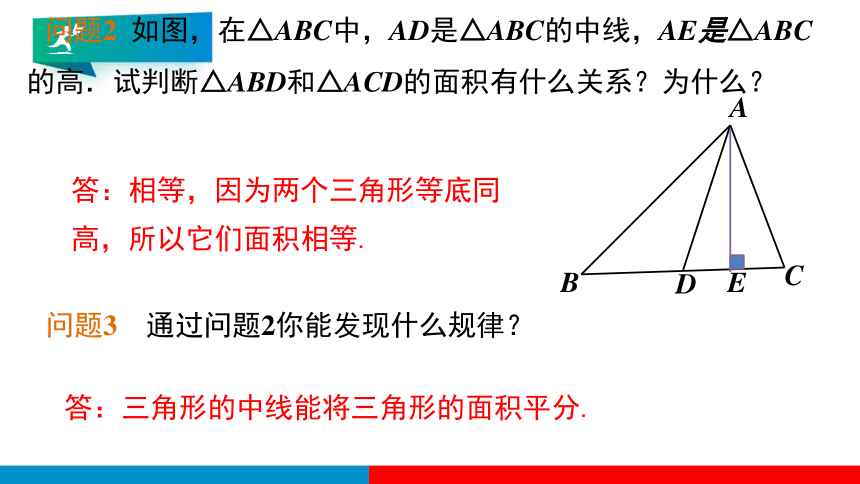
问题2 如图,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?为什么?
B
C
D
E
A
答:相等,因为两个三角形等底同高,所以它们面积相等.
问题3 通过问题2你能发现什么规律?
答:三角形的中线能将三角形的面积平分.
归纳总结:
1.三角形的三条中线相交于一点,三角形三条中线的交点叫做三角形的重心.
2.三角形的中线将三角形分成面积相等的两部分.
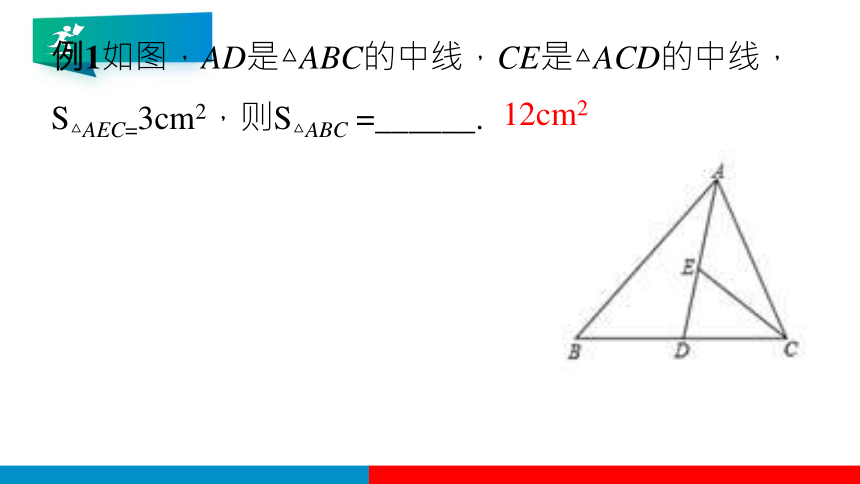
例1如图,AD是△ABC的中线,CE是△ACD的中线,S△AEC=3cm2,则S△ABC =______.
12cm2
变式:如何将三角形ABC分成面积相等的4份?
例2:如图,在△ABC中,CD是中线,已知△DBC与△ADC的周长差是3cm, AC=8cm,求BC的长.
A
D
B
C
解: ∵CD是△ABC的中线,
∴BD=AD .
∵△DBC与△ADC的周长差是3cm.
∴ BC-AC=3cm.
∵ AC=8cm,
∴ BC=11cm.
归纳:三角形中线把三角形分成两个三角形,两个三角形的周长差其实就是另外两边的差,即△DBC与△ADC的周长差=BC-AC
解析:∵BM是△ABC的中线,
∴MA=MC,
∴C△ABM-C△BCM
=AB+BM+MA-BC-CM-BM
=AB-BC=5-3=2cm.
答:△ABM与△BCM的周长是差是2cm.
练习:如图,BM是△ABC的中线,AB=5cm,BC=3cm,那么△ABM与△BCM的周长的差是多少?
例3
练习:下列说法正确的是 ( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可
能在三角形外
D.三角形的角平分线是射线
B
例4如图,在△ABC中,CD是中线,已知BC-AC=5cm, △DBC的周长为25cm,求△ADC的周长.
A
D
B
C
解: ∵CD是△ABC的中线,
∴BD=AD .
∵BC-AC=5cm,
∴ △DBC与△ADC的周长差是5cm.
又∵ △DBC的周长为25cm,
∴ △ADC的周长为25-5=20(cm).
能力提升:王大爷有一块三角形的菜地,现在要将它们平均分给四个儿子,在菜地的一角A处有一口池塘,为了使分开后的四块菜地都就近取水,王大爷为此很伤脑筋.你能想出什么办法帮帮王大爷吗?
如果不考虑水源,你认为还可以怎样分
A
(思路提示:想到三角形的中线能把三角形分成面积相等的两部分.)
https://www.21cnjy.com/help/help_extract.php
11.1 与三角形有关的线段
11.1.2第3课时三角形的中线
精品同步教学课件
问题1 如图,如果点D是线段BC的中点,那么线段AD就称为△ABC的中线.试说明什么叫三角形的中线?
A
B
C
定义:
如图,连接△ABC的顶点和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线.
想一想:由三角形的中线能得到什么结论?
BD=CD= BC
D
三角形的中线
一
A
B
C
D
∵ AD是△ABC的边BC上的中线.
∴BD=CD=BC
三角形中线的符号语言
∵ BD=CD=BC
∴AD是△ABC的边BC上的中线.
画一画:如图,分别画出锐角三角形、直角三角形、钝角三角形的三条中线,并观察它们中线的交点有什么规律?
画图发现
三角形的三条中线交于三角形内部一点,这一点我们称为三角形的重心.
A
B
C
A
B
C
A
B
C
D
E
F
D
D
E
F
E
F
O
O
O
问题2 如图,在△ABC中,AD是△ABC的中线,AE是△ABC的高.试判断△ABD和△ACD的面积有什么关系?为什么?
B
C
D
E
A
答:相等,因为两个三角形等底同高,所以它们面积相等.
问题3 通过问题2你能发现什么规律?
答:三角形的中线能将三角形的面积平分.
归纳总结:
1.三角形的三条中线相交于一点,三角形三条中线的交点叫做三角形的重心.
2.三角形的中线将三角形分成面积相等的两部分.
例1如图,AD是△ABC的中线,CE是△ACD的中线,S△AEC=3cm2,则S△ABC =______.
12cm2
变式:如何将三角形ABC分成面积相等的4份?
例2:如图,在△ABC中,CD是中线,已知△DBC与△ADC的周长差是3cm, AC=8cm,求BC的长.
A
D
B
C
解: ∵CD是△ABC的中线,
∴BD=AD .
∵△DBC与△ADC的周长差是3cm.
∴ BC-AC=3cm.
∵ AC=8cm,
∴ BC=11cm.
归纳:三角形中线把三角形分成两个三角形,两个三角形的周长差其实就是另外两边的差,即△DBC与△ADC的周长差=BC-AC
解析:∵BM是△ABC的中线,
∴MA=MC,
∴C△ABM-C△BCM
=AB+BM+MA-BC-CM-BM
=AB-BC=5-3=2cm.
答:△ABM与△BCM的周长是差是2cm.
练习:如图,BM是△ABC的中线,AB=5cm,BC=3cm,那么△ABM与△BCM的周长的差是多少?
例3
练习:下列说法正确的是 ( )
A.三角形三条高都在三角形内
B.三角形三条中线相交于一点
C.三角形的三条角平分线可能在三角形内,也可
能在三角形外
D.三角形的角平分线是射线
B
例4如图,在△ABC中,CD是中线,已知BC-AC=5cm, △DBC的周长为25cm,求△ADC的周长.
A
D
B
C
解: ∵CD是△ABC的中线,
∴BD=AD .
∵BC-AC=5cm,
∴ △DBC与△ADC的周长差是5cm.
又∵ △DBC的周长为25cm,
∴ △ADC的周长为25-5=20(cm).
能力提升:王大爷有一块三角形的菜地,现在要将它们平均分给四个儿子,在菜地的一角A处有一口池塘,为了使分开后的四块菜地都就近取水,王大爷为此很伤脑筋.你能想出什么办法帮帮王大爷吗?
如果不考虑水源,你认为还可以怎样分
A
(思路提示:想到三角形的中线能把三角形分成面积相等的两部分.)
https://www.21cnjy.com/help/help_extract.php
