11.2.1 第1课时 三角形的内角和 课件(共20页)
文档属性
| 名称 | 11.2.1 第1课时 三角形的内角和 课件(共20页) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 16:58:49 | ||
图片预览



文档简介
(共20张PPT)
11.2 与三角形有关的角
11.2.1 三角形的内角
精品同步教学课件
第1课时 三角形的内角和证明
我的形状最小,那我的内角和最小.
我的形状最大,那我的内角和最大.
不对,我有一个钝角,所以我的内角和才是最大的.
一天,三类三角形通过对自身的特点,讲出了自己对三角形内角和的理解,请同学们作为小判官给它们评判一下吧.
导入新课
我们在小学已经知道,任意一个三角形的内角和等于180°,与三角形的形状、大小无关,所以它们的说法都是错误的.
思考:你有什么办法可以验证三角形的内角和为180°呢
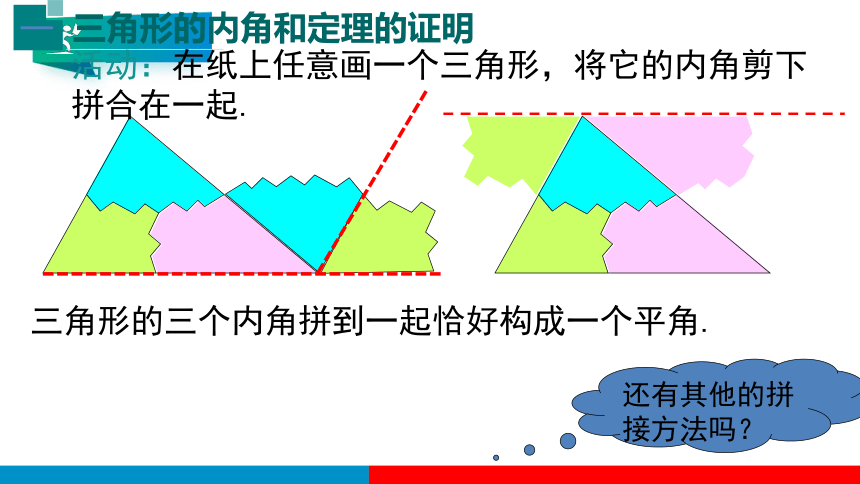
三角形的三个内角拼到一起恰好构成一个平角.
还有其他的拼接方法吗?
三角形的内角和定理的证明
一
活动:在纸上任意画一个三角形,将它的内角剪下拼合在一起.
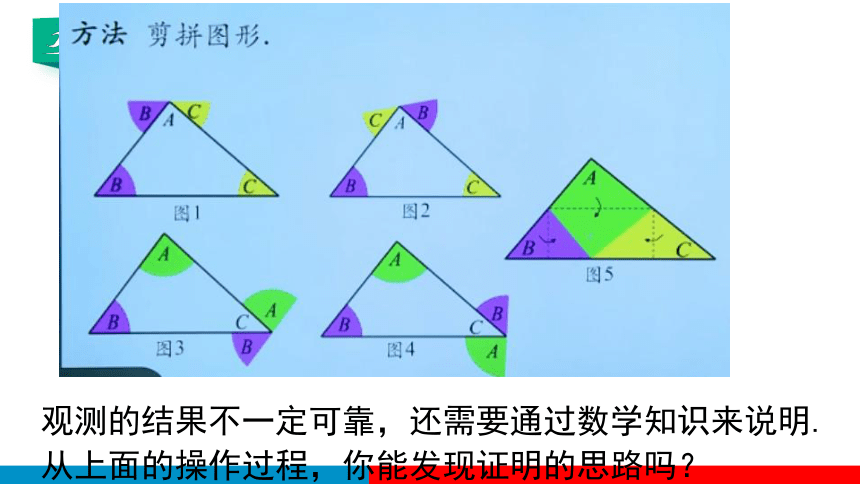
观测的结果不一定可靠,还需要通过数学知识来说明.从上面的操作过程,你能发现证明的思路吗?
验证结论
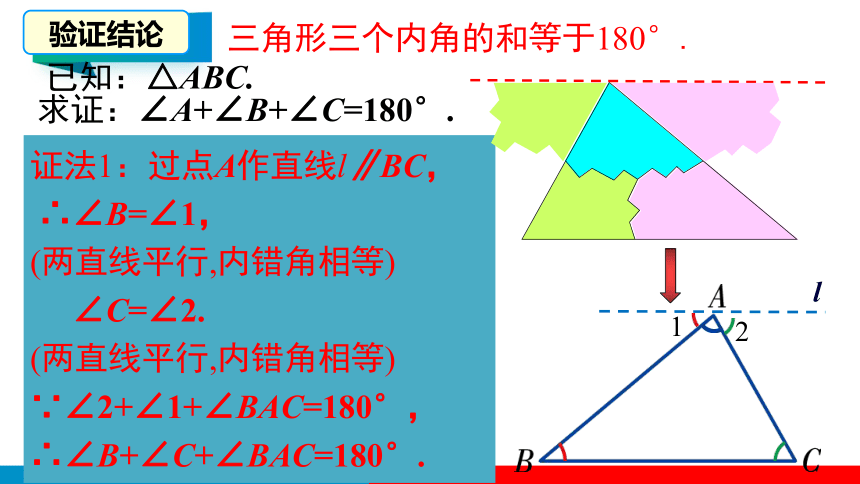
三角形三个内角的和等于180°.
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证法1:过点A作直线l∥BC,
∴∠B=∠1,
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
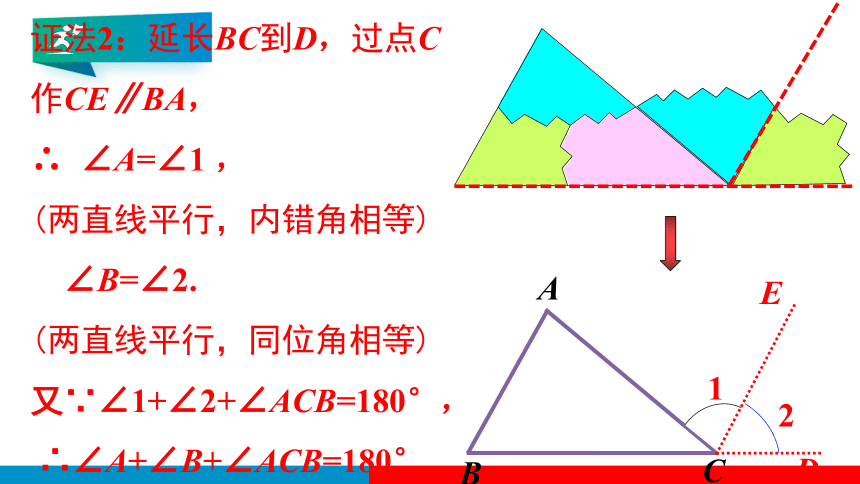
证法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 ,
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
C
B
A
E
D
F
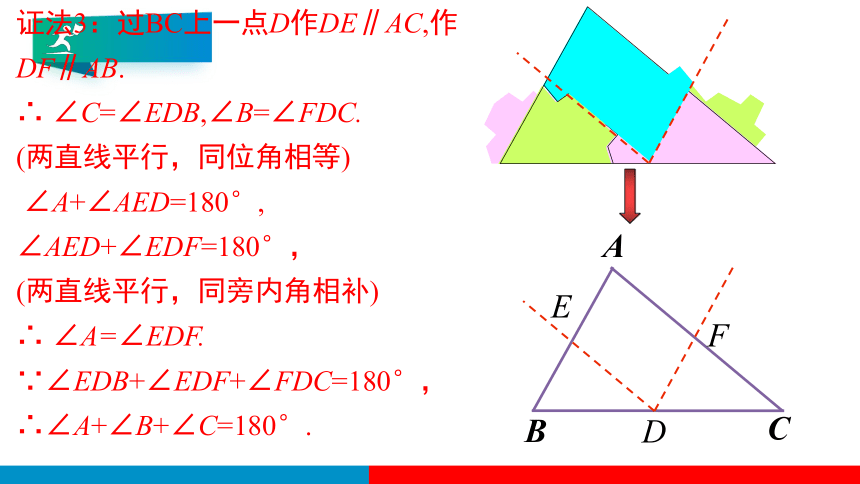
证法3:过BC上一点D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,
∴∠A+∠B+∠C=180°.
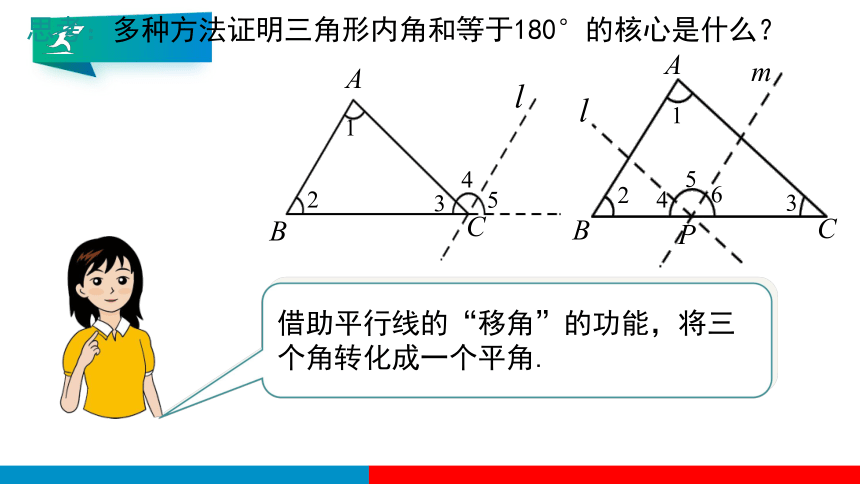
思考:多种方法证明三角形内角和等于180°的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
思路总结
为了证明三个角的和为180°,转化为一个平角,这种转化思想是数学中的常用方法.
想一想:还有其他的证法吗?还有其他办法得到180度吗?
两直线平行,同旁内角互补。
证法4
证法5
三角形内角和定理
几何语言:在△ABC中,
∠A+∠B+∠C=180°
定理内容:三角形三个内角的和等于180°.
练习:求出下列各图中的x值.
x=70
x=60
x=30
x=50
例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:∵∠BAC=40 °, AD是△ABC的角平分线
∴∠BAD= ∠BAC=20 °.
∵在△ABD中,∠B=75 °,∠BAD=20°
∴∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
三角形的内角和定理的运用
二
小结
C
2
4
A
B
3
E
Q
D
F
P
G
H
1
B
G
C
2
4
A
3
E
D
F
H
1
试一试:同学们按照上图中的辅助线,给出证明步骤?
拓展
1.在△ABC中,∠A :∠B:∠C=1:2:3,则△ABC是
_________三角形 .
针对训练
2.在△ABC中, ∠A= ∠B+10°, ∠C= ∠A + 10°, 则 ∠A= , ∠ B= ,∠ C= .
直角
60°
50°
70°
https://www.21cnjy.com/help/help_extract.php
11.2 与三角形有关的角
11.2.1 三角形的内角
精品同步教学课件
第1课时 三角形的内角和证明
我的形状最小,那我的内角和最小.
我的形状最大,那我的内角和最大.
不对,我有一个钝角,所以我的内角和才是最大的.
一天,三类三角形通过对自身的特点,讲出了自己对三角形内角和的理解,请同学们作为小判官给它们评判一下吧.
导入新课
我们在小学已经知道,任意一个三角形的内角和等于180°,与三角形的形状、大小无关,所以它们的说法都是错误的.
思考:你有什么办法可以验证三角形的内角和为180°呢
三角形的三个内角拼到一起恰好构成一个平角.
还有其他的拼接方法吗?
三角形的内角和定理的证明
一
活动:在纸上任意画一个三角形,将它的内角剪下拼合在一起.
观测的结果不一定可靠,还需要通过数学知识来说明.从上面的操作过程,你能发现证明的思路吗?
验证结论
三角形三个内角的和等于180°.
求证:∠A+∠B+∠C=180°.
已知:△ABC.
证法1:过点A作直线l∥BC,
∴∠B=∠1,
(两直线平行,内错角相等)
∠C=∠2.
(两直线平行,内错角相等)
∵∠2+∠1+∠BAC=180°,
∴∠B+∠C+∠BAC=180°.
1
2
证法2:延长BC到D,过点C作CE∥BA,
∴ ∠A=∠1 ,
(两直线平行,内错角相等)
∠B=∠2.
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°,
∴∠A+∠B+∠ACB=180°.
C
B
A
E
D
1
2
C
B
A
E
D
F
证法3:过BC上一点D作DE∥AC,作DF∥AB.
∴ ∠C=∠EDB,∠B=∠FDC.
(两直线平行,同位角相等)
∠A+∠AED=180°,
∠AED+∠EDF=180°,
(两直线平行,同旁内角相补)
∴ ∠A=∠EDF.
∵∠EDB+∠EDF+∠FDC=180°,
∴∠A+∠B+∠C=180°.
思考:多种方法证明三角形内角和等于180°的核心是什么?
借助平行线的“移角”的功能,将三个角转化成一个平角.
C
A
B
1
2
3
4
5
l
A
C
B
1
2
3
4
5
l
P
6
m
思路总结
为了证明三个角的和为180°,转化为一个平角,这种转化思想是数学中的常用方法.
想一想:还有其他的证法吗?还有其他办法得到180度吗?
两直线平行,同旁内角互补。
证法4
证法5
三角形内角和定理
几何语言:在△ABC中,
∠A+∠B+∠C=180°
定理内容:三角形三个内角的和等于180°.
练习:求出下列各图中的x值.
x=70
x=60
x=30
x=50
例1 如图,在△ABC中, ∠BAC=40 °, ∠B=75 °,AD是△ABC的角平分线,求∠ADB的度数.
A
B
C
D
解:∵∠BAC=40 °, AD是△ABC的角平分线
∴∠BAD= ∠BAC=20 °.
∵在△ABD中,∠B=75 °,∠BAD=20°
∴∠ADB=180°-∠B-∠BAD
=180°-75°-20°
=85°.
三角形的内角和定理的运用
二
小结
C
2
4
A
B
3
E
Q
D
F
P
G
H
1
B
G
C
2
4
A
3
E
D
F
H
1
试一试:同学们按照上图中的辅助线,给出证明步骤?
拓展
1.在△ABC中,∠A :∠B:∠C=1:2:3,则△ABC是
_________三角形 .
针对训练
2.在△ABC中, ∠A= ∠B+10°, ∠C= ∠A + 10°, 则 ∠A= , ∠ B= ,∠ C= .
直角
60°
50°
70°
https://www.21cnjy.com/help/help_extract.php
