华师大版八年级上册 13.2 三角形全等的判定(第2课时 ) 课件(共21张PPT)
文档属性
| 名称 | 华师大版八年级上册 13.2 三角形全等的判定(第2课时 ) 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 619.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 18:29:36 | ||
图片预览








文档简介
(共21张PPT)
第13章 全等三角形
13.2 全等三角形
第2课时 全等三角形的判定—边角边
学习目标
3
1
2
通过画、量、观察、比较和猜想等过程,探索、归纳、证明两个三角形全等的条件——SAS.
掌握用SAS证明两个三角形全等的方法,并能综合运用全等三角形的性质证明线段和角相等.(重、难点)
了解“SSA”不能作为证明两个三角形全等的条件.
A
B
C
D
E
F
1. 什么叫全等三角形?
能够完全重合的两个三角形叫做全等三角形.
3.已知△ABC ≌△DEF,找出其中相等的边与角.
①AB=DE
③ CA=FD
② BC=EF
④ ∠A= ∠D
⑤ ∠B=∠E
⑥ ∠C= ∠F
2. 全等三角形有什么性质?
全等三角形的对应边相等,对应角相等.
知识回顾
知识讲解
探究:
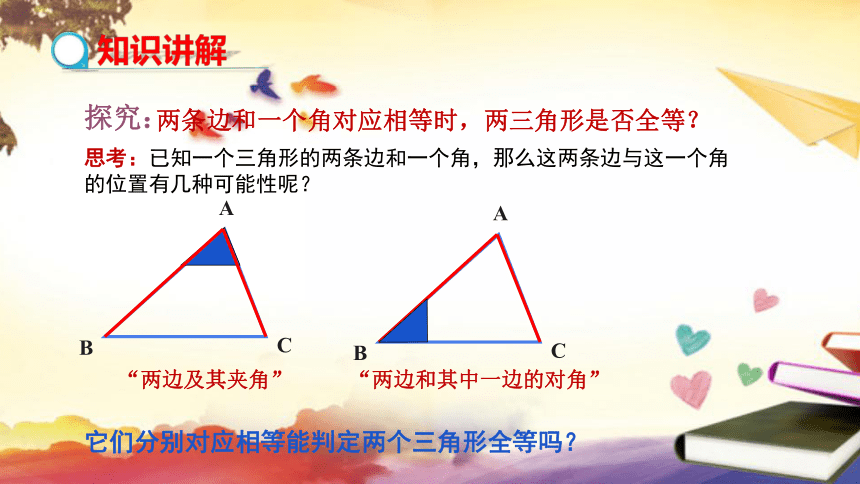
两条边和一个角对应相等时,两三角形是否全等?
思考:已知一个三角形的两条边和一个角,那么这两条边与这一个角 的位置有几种可能性呢?
A
B
C
A
B
C
“两边及其夹角”
“两边和其中一边的对角”
它们分别对应相等能判定两个三角形全等吗?
做一做:画△ABC,使AB=3cm,AC=5cm.
画法:
1. 画线段AB= 3cm;
3. 在射线AM上截取AC=5cm;
这样画出来的三角形与同桌所画的三角形进行比较,它们互相重合吗?
若再加一个条件,使∠A=45°,画出△ABC.
2. 画∠MAB= 45°;
4. 连接BC.
△ABC就是所求的三角形.
把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?
A
B
C
A′
B ′
C ′
想一想:作图的结果反映了什么规律?你能用文字语言和符号语言概括吗?
下面用叠合的方法,看看你和你同伴所画的两个三角形是否可以完全重合.
文字语言:两边及其夹角分别相等的两个三角形全等.
(简写成“边角边”或“SAS”)
A
B
C
D
E
F
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SAS).
几何语言:
三角形全等的基本事实:边角边(S.A.S.)
AB = DE,
∠A =∠D,
AC =DF ,
已知:如图,AE=DE, BE=CE.
求证:△ABE≌△DCE.
证明:在△ABE和△DCE中,
∵ AE=DE(已知),
∠AEB=∠DEC(对顶角相等),
BE=CE(公共边) ,
∴ △ABE≌△DCE (S.A.S.).
例1
如图,下列哪组条件不能判定△ABC≌△DEF( )
A
B
C
D
E
F
AB=DE,
A. ∠A=∠D,
AC=DF
AC=DF,
C. ∠C=∠F,
BC=EF
AB=DE,
B. ∠B=∠E,
BC=EF
AC=DF,
D. ∠B=∠E,
BC=EF
D
练一练
已知:如图,AD∥BC,AD=CB.
求证: △ADC≌△CBA
A
B
C
D
1
2
想一想
证明:∵AD∥BC,
∴ ∠1=∠2(两直线平行,内错角相等).
在△ADC和△CBA中, ∵
∴ △ADC≌△CBA(S.A.S.).
归纳:
(1)准备条件:证全等时要用的条件要先证好;
(2)三角形全等书写三步骤:
①写出在哪两个三角形中;
②摆出三个条件(注意:按定理名称的顺序书写);
③写出全等结论.
证明的书写步骤:
如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连接AC并延长到D, 使CD=CA.连接BC并延长到E,使CE=CB. 连接DE,那么量出DE的长,就是A、B的距离.为什么?
A
B
C
E
D
证明:在△ABC 和△DEC中,
∴△ABC ≌△DEC.(S.A.S.)
∴AB=DE.(全等三角形的对应边相等)
例2
CA = CD,
∠ACB =∠DCE,
CB =CE ,
已知:如图,AB=AC,AD=AE.
求证: △ABE≌△ACD
A
C
D
B
E
A
证明:在△ABE和△ACD中
∵ AB=AC(已知)
∠A=∠A(公共角)
AD=AE(已知)
∴ △ABE≌△ACD(S.A.S.)
想一想
A
45°
B
B′
C
10cm
8cm
8cm
探究:两边和其中一边的对角对应相等时,两三角形是否全等?
试一试:以10cm,8cm为三角形的两边,长度为8cm的边所对的角为45°,动手画一画,你发现了什么?
△ABC 的形状与大小是唯一确定的吗
10cm
′
45°
8cm
8cm
45°
10cm
结论:两边及其一边所对的角相等,两个三角形不一定全等。
发现:△ABC和△ AB'C 满足AC=AC ,BC= B'C ,∠A=∠A,
但△ABC与△ AB'C 不全等.
随堂训练
1.如图,去修补一块玻璃,问带哪一块玻璃去可以使得新玻璃与原来的完全一样?
Ⅰ
Ⅱ
Ⅲ
知识应用
分析:带Ⅲ去,可以根据SAS得到与原三角形全等的一个三角形.
2.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是( )
A.∠A=∠D B.∠E=∠C
C.∠A=∠C D.∠ABD=∠EBC
D
3. 如图,点A、E、B、D在同一条直线上,AE=DB,AC=DF,AC∥DF.请探索BC与EF有怎样的数量和位置关系?并说明理由.
_
F
_
E
_
B
_
A
_
C
_
D
AC=DF, (已知)
∠A=∠D ,(已证)
AB =DE, (已证)
∴△ BCA ≌△ EFD . (SAS)
解:∵AC∥DF,
∴∠A=∠D.(两直线平行,内错角相等)
又∵ AE=DB, ∴ AE +BE =DB +BE,即AB =DE.
在△BCA 和△EFD 中,
∴ BC= EF,( )
∴ ∠ABC=∠DEF,(全等三角形的对应角相等)
∴EF‖BC.(内错角相等,两直线平行)
全等三角形的对应边相等
_
F
_
E
_
B
_
A
_
C
_
D
课堂小结
2.用SAS证明两个三角形全等时,已知两边,必须找“夹角”;已知一角和这角的一夹边,必须找这角的另一夹边.
1. 三角形全等的条件:两边和它们的夹角对应相等的两个三角形全等. (边角边或SAS)
3.利用全等三角形证明线段或角相等,其思路如下:
⑴观察要证的线段和角在哪两个可能全等三角形之中;
⑵分析要证全等的这两个三角形,已知什么条件,还缺什么条件.
第13章 全等三角形
13.2 全等三角形
第2课时 全等三角形的判定—边角边
学习目标
3
1
2
通过画、量、观察、比较和猜想等过程,探索、归纳、证明两个三角形全等的条件——SAS.
掌握用SAS证明两个三角形全等的方法,并能综合运用全等三角形的性质证明线段和角相等.(重、难点)
了解“SSA”不能作为证明两个三角形全等的条件.
A
B
C
D
E
F
1. 什么叫全等三角形?
能够完全重合的两个三角形叫做全等三角形.
3.已知△ABC ≌△DEF,找出其中相等的边与角.
①AB=DE
③ CA=FD
② BC=EF
④ ∠A= ∠D
⑤ ∠B=∠E
⑥ ∠C= ∠F
2. 全等三角形有什么性质?
全等三角形的对应边相等,对应角相等.
知识回顾
知识讲解
探究:
两条边和一个角对应相等时,两三角形是否全等?
思考:已知一个三角形的两条边和一个角,那么这两条边与这一个角 的位置有几种可能性呢?
A
B
C
A
B
C
“两边及其夹角”
“两边和其中一边的对角”
它们分别对应相等能判定两个三角形全等吗?
做一做:画△ABC,使AB=3cm,AC=5cm.
画法:
1. 画线段AB= 3cm;
3. 在射线AM上截取AC=5cm;
这样画出来的三角形与同桌所画的三角形进行比较,它们互相重合吗?
若再加一个条件,使∠A=45°,画出△ABC.
2. 画∠MAB= 45°;
4. 连接BC.
△ABC就是所求的三角形.
把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?
A
B
C
A′
B ′
C ′
想一想:作图的结果反映了什么规律?你能用文字语言和符号语言概括吗?
下面用叠合的方法,看看你和你同伴所画的两个三角形是否可以完全重合.
文字语言:两边及其夹角分别相等的两个三角形全等.
(简写成“边角边”或“SAS”)
A
B
C
D
E
F
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SAS).
几何语言:
三角形全等的基本事实:边角边(S.A.S.)
AB = DE,
∠A =∠D,
AC =DF ,
已知:如图,AE=DE, BE=CE.
求证:△ABE≌△DCE.
证明:在△ABE和△DCE中,
∵ AE=DE(已知),
∠AEB=∠DEC(对顶角相等),
BE=CE(公共边) ,
∴ △ABE≌△DCE (S.A.S.).
例1
如图,下列哪组条件不能判定△ABC≌△DEF( )
A
B
C
D
E
F
AB=DE,
A. ∠A=∠D,
AC=DF
AC=DF,
C. ∠C=∠F,
BC=EF
AB=DE,
B. ∠B=∠E,
BC=EF
AC=DF,
D. ∠B=∠E,
BC=EF
D
练一练
已知:如图,AD∥BC,AD=CB.
求证: △ADC≌△CBA
A
B
C
D
1
2
想一想
证明:∵AD∥BC,
∴ ∠1=∠2(两直线平行,内错角相等).
在△ADC和△CBA中, ∵
∴ △ADC≌△CBA(S.A.S.).
归纳:
(1)准备条件:证全等时要用的条件要先证好;
(2)三角形全等书写三步骤:
①写出在哪两个三角形中;
②摆出三个条件(注意:按定理名称的顺序书写);
③写出全等结论.
证明的书写步骤:
如图,有一池塘,要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B 的点C,连接AC并延长到D, 使CD=CA.连接BC并延长到E,使CE=CB. 连接DE,那么量出DE的长,就是A、B的距离.为什么?
A
B
C
E
D
证明:在△ABC 和△DEC中,
∴△ABC ≌△DEC.(S.A.S.)
∴AB=DE.(全等三角形的对应边相等)
例2
CA = CD,
∠ACB =∠DCE,
CB =CE ,
已知:如图,AB=AC,AD=AE.
求证: △ABE≌△ACD
A
C
D
B
E
A
证明:在△ABE和△ACD中
∵ AB=AC(已知)
∠A=∠A(公共角)
AD=AE(已知)
∴ △ABE≌△ACD(S.A.S.)
想一想
A
45°
B
B′
C
10cm
8cm
8cm
探究:两边和其中一边的对角对应相等时,两三角形是否全等?
试一试:以10cm,8cm为三角形的两边,长度为8cm的边所对的角为45°,动手画一画,你发现了什么?
△ABC 的形状与大小是唯一确定的吗
10cm
′
45°
8cm
8cm
45°
10cm
结论:两边及其一边所对的角相等,两个三角形不一定全等。
发现:△ABC和△ AB'C 满足AC=AC ,BC= B'C ,∠A=∠A,
但△ABC与△ AB'C 不全等.
随堂训练
1.如图,去修补一块玻璃,问带哪一块玻璃去可以使得新玻璃与原来的完全一样?
Ⅰ
Ⅱ
Ⅲ
知识应用
分析:带Ⅲ去,可以根据SAS得到与原三角形全等的一个三角形.
2.如图,AB=DB,BC=BE,欲证△ABE≌△DBC,则需要增加的条件是( )
A.∠A=∠D B.∠E=∠C
C.∠A=∠C D.∠ABD=∠EBC
D
3. 如图,点A、E、B、D在同一条直线上,AE=DB,AC=DF,AC∥DF.请探索BC与EF有怎样的数量和位置关系?并说明理由.
_
F
_
E
_
B
_
A
_
C
_
D
AC=DF, (已知)
∠A=∠D ,(已证)
AB =DE, (已证)
∴△ BCA ≌△ EFD . (SAS)
解:∵AC∥DF,
∴∠A=∠D.(两直线平行,内错角相等)
又∵ AE=DB, ∴ AE +BE =DB +BE,即AB =DE.
在△BCA 和△EFD 中,
∴ BC= EF,( )
∴ ∠ABC=∠DEF,(全等三角形的对应角相等)
∴EF‖BC.(内错角相等,两直线平行)
全等三角形的对应边相等
_
F
_
E
_
B
_
A
_
C
_
D
课堂小结
2.用SAS证明两个三角形全等时,已知两边,必须找“夹角”;已知一角和这角的一夹边,必须找这角的另一夹边.
1. 三角形全等的条件:两边和它们的夹角对应相等的两个三角形全等. (边角边或SAS)
3.利用全等三角形证明线段或角相等,其思路如下:
⑴观察要证的线段和角在哪两个可能全等三角形之中;
⑵分析要证全等的这两个三角形,已知什么条件,还缺什么条件.
