三角函数图形变换(1)[下学期]
图片预览


文档简介
课题:4.9.1 函数的图象(1)
教学目的:1)理解振幅的定义;
2) 理解振幅变换和周期变换的规律,会对函数进行振幅和周期变换;
3) 培养动与静的辩证关系,提高数学修养.
教学重点:1) 理解振幅变换和周期变换的规律;
2) 熟练的对函数进行振幅和周期变换.
教学难点:理解振幅变换和周期变换的规律.
教学方法:启发引导式(引导学生结合作图过程和动态的变换过程理解振幅变换和周期变换的规律)
教学地点:多媒体教室.
应用软件:几何画板
一、课题引入
『老师』在我们前面的学习中,我们已经解决了函数与函数的图象与性质。在作图时我们还学习了一种作图的方法:五点作图法。请大家回忆五点作图法作的图时在X轴上的五个值取的是?函数的主要性质有哪些?
『学生』五点作图法作的图时在X轴上的五个值取的是
主要性质有:定义域:R 值 域:[-1,1] 周 期:
奇偶性:是奇函数;是偶函数.
单调性
『老师』很好,在实际生活中啊,我们常常会遇到的不是这样简单的函数,而是形如的函数解析式(其中都是常数)。这样的函数图象是什么样子的呢?它的性质与比较发生了哪些变换呢?
二、讲解新课
首先我们一起来研究形如的图象与性质。
例1.画出函数与的简图;
解:画简图,我们用“五点作图法”
这两个函数都是周期函数,且周期为
我们先画它们在[0,]上的简图。
注意:“五点法作图”的步骤为:列表,描点,连线。
列表1:
0
0 1 0 -1 0
0 2 0 -2 0
0 0 0
描点画图:
然后我们利用其周期性,把它们在[0,]上的简图向左,右分别扩展,便可得到它们的简图。
『老师』大家思考一下:把它们与比较,有什么联系?其哪些性质发生了变化?
(师生一起):1、的图象可以看作把上所有的点的纵坐标伸长到原来的2倍(横坐标不变)而得到;
函数的值域变为了[-2,2]
2、的图象可以看作把上所有的点的纵坐标缩短到原来的倍(横坐标不变)而得到;
函数的值域变为了[]
『老师』再请大家思考:如果换成一般情况,你能归纳出它与 的联系吗?
(师生一起): 一般地,函数, (其A>0,且A1)的图象,可以看作是把正弦曲线上所有点的纵坐标伸长(当A>1时)或缩短(当0函数的值域是[-A,A],
在物理上,A称为振幅,我们把这种变换称为振幅变换。
说明:这要注意以下几点
1) 在变动中,变的是纵坐标,不变的是横坐标,伸长时A>1,缩短时02) 规定的A>0,解释振幅的定义:物体离开平衡位置的距离。
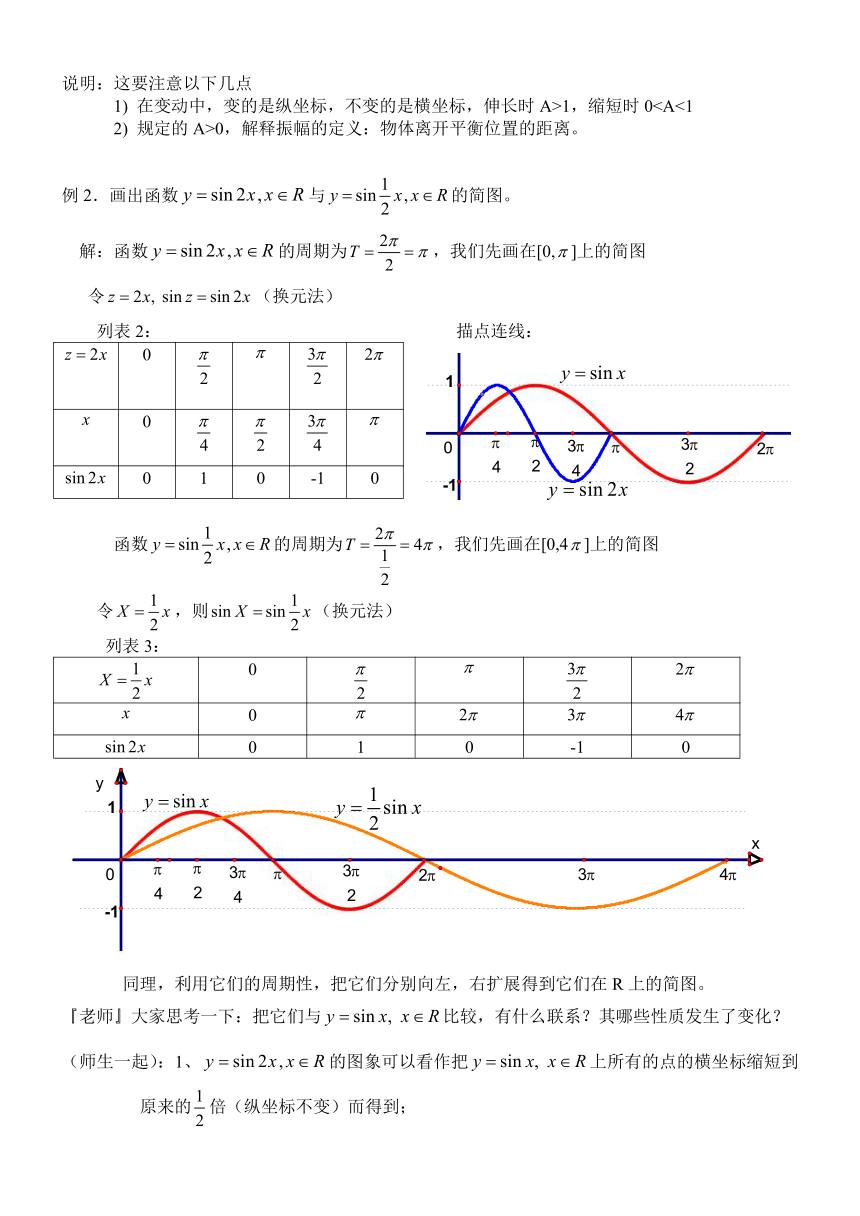
例2.画出函数与的简图。
解:函数的周期为,我们先画在[0,]上的简图
令(换元法)
列表2: 描点连线:
0
0
0 1 0 -1 0
函数的周期为,我们先画在[0,4]上的简图
令,则(换元法)
列表3:
0
0
0 1 0 -1 0
同理,利用它们的周期性,把它们分别向左,右扩展得到它们在R上的简图。
『老师』大家思考一下:把它们与比较,有什么联系?其哪些性质发生了变化?
(师生一起):1、的图象可以看作把上所有的点的横坐标缩短到原来的倍(纵坐标不变)而得到;
函数的定义域、值域和奇偶性不变,周期变为原来的倍,单调区间也发生了改变。
2、的图象可以看作把上所有的点的横坐标伸长到原来的2倍(纵坐标不变)而得到;
函数的定义域、值域和奇偶性不变,周期变为原来的2倍,单调区间也发生了改变。
『老师』再请大家思考:如果换成一般情况,你能归纳出它与的联系吗?(学生先回答)
(师生一起): 一般地,函数, (其>0,且1)的图象,可以看作是把正弦曲线上所有点的横坐标伸长(当0<<1时)或缩短(当>1时)到原来的倍(纵坐标不变)而得到.
函数的中决定了其周期,所以我们把这一变换称为周期变换。
说明:1)列表时,x轴上的五个值怎样计算:换元法,解5个一元一次方程。
2)周期变换中,强调是“x轴上的所有点伸长或缩短”;“纵坐标不变”。
3)强调与振幅变换的区别:振幅变换是原来的A倍,周期变换是原来的。
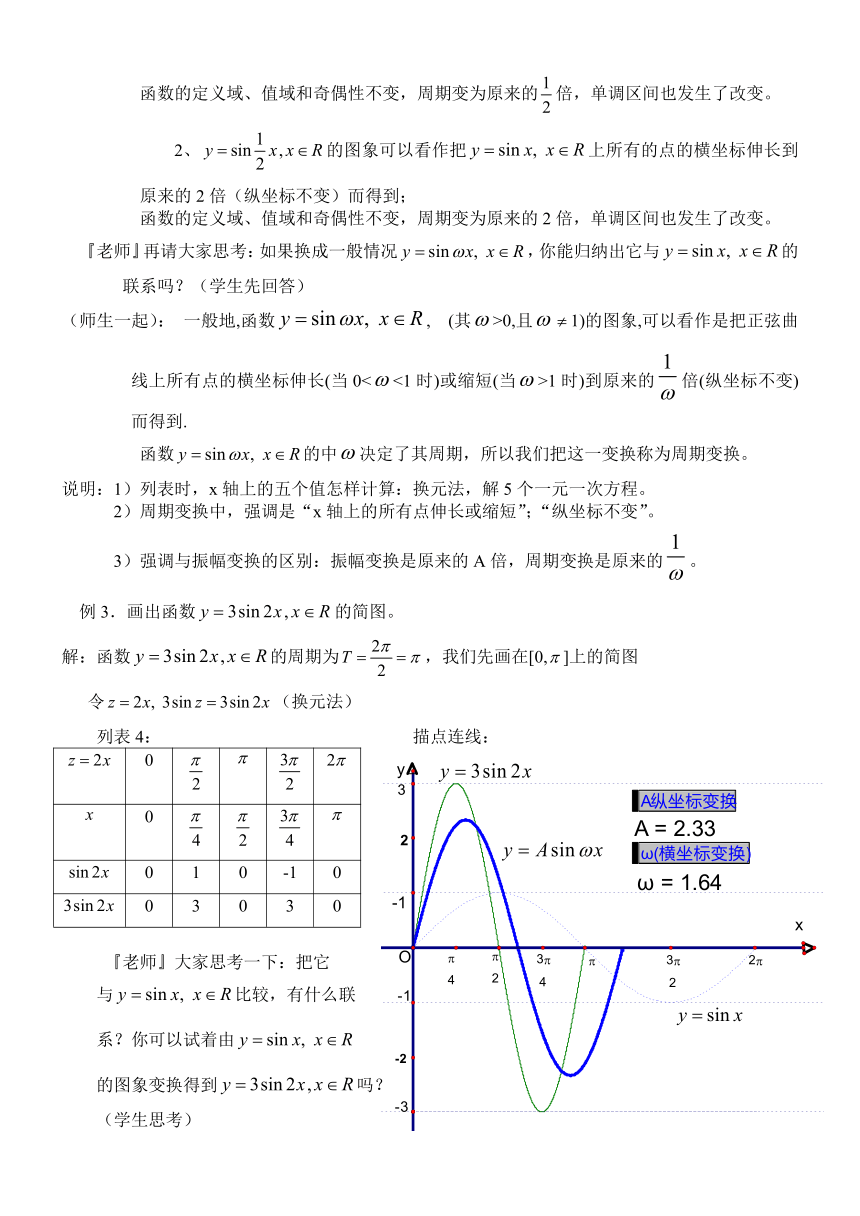
例3.画出函数的简图。
解:函数的周期为,我们先画在[0,]上的简图
令(换元法)
列表4: 描点连线:
0
0
0 1 0 -1 0
0 3 0 3 0
『老师』大家思考一下:把它
与比较,有什么联
系?你可以试着由
的图象变换得到吗?
(学生思考)
『学生1』先把的
纵坐标伸长到原来的3倍(横坐标不变),得到,再把横坐标缩短到原来的倍(纵坐标不变),得到。
『学生2』先把的横坐标缩短到原来的倍(纵坐标不变),得到,再把纵坐标伸长到原来的3倍(横坐标不变),得到。
说明:启发引导学生自己的出结论,如果较困难,可以适当提醒。
三、课堂练习:
P73练习1、在坐标纸上作出下列函数在一个周期上的简图
(1) (2)
并说出它们可以由通过怎样的变换而得到?.
P74练习2、3(学生口答)
2、函数的振幅是多少?它的图象与正弦曲线有什么关系?
答案:振幅是,把正弦曲线上的纵坐标缩短到原来的倍,横坐标不变可得到它的图象。
3、函数的周期是什么?它的图象与正弦曲线有什么关系?
答案:振幅是,把正弦曲线上的横坐标伸长到原来的倍,纵坐标不变可得到它的图象。
四、课时小结:今天我们一起研究了形如的函数图象,它的图象可以通过的图象进行振幅变换和周期变换而得来,那么我们就要理解并学会对函数进行振幅变换;周期变换。
五、课后作业:1)预习课本P69例3;
2)习题4.9——P76:第二题——(1)(2)
3)目标训练二十六
4)复习函数的平移变换与今天的内容。
六、板书设计:
4.9.1 函数的图象(1)
复习:正弦、余弦函数的性质
新课: (振幅变换); (周期变换)
小结:
附1
附2
附3
附4
附5
附6
附7
附8
教学目的:1)理解振幅的定义;
2) 理解振幅变换和周期变换的规律,会对函数进行振幅和周期变换;
3) 培养动与静的辩证关系,提高数学修养.
教学重点:1) 理解振幅变换和周期变换的规律;
2) 熟练的对函数进行振幅和周期变换.
教学难点:理解振幅变换和周期变换的规律.
教学方法:启发引导式(引导学生结合作图过程和动态的变换过程理解振幅变换和周期变换的规律)
教学地点:多媒体教室.
应用软件:几何画板
一、课题引入
『老师』在我们前面的学习中,我们已经解决了函数与函数的图象与性质。在作图时我们还学习了一种作图的方法:五点作图法。请大家回忆五点作图法作的图时在X轴上的五个值取的是?函数的主要性质有哪些?
『学生』五点作图法作的图时在X轴上的五个值取的是
主要性质有:定义域:R 值 域:[-1,1] 周 期:
奇偶性:是奇函数;是偶函数.
单调性
『老师』很好,在实际生活中啊,我们常常会遇到的不是这样简单的函数,而是形如的函数解析式(其中都是常数)。这样的函数图象是什么样子的呢?它的性质与比较发生了哪些变换呢?
二、讲解新课
首先我们一起来研究形如的图象与性质。
例1.画出函数与的简图;
解:画简图,我们用“五点作图法”
这两个函数都是周期函数,且周期为
我们先画它们在[0,]上的简图。
注意:“五点法作图”的步骤为:列表,描点,连线。
列表1:
0
0 1 0 -1 0
0 2 0 -2 0
0 0 0
描点画图:
然后我们利用其周期性,把它们在[0,]上的简图向左,右分别扩展,便可得到它们的简图。
『老师』大家思考一下:把它们与比较,有什么联系?其哪些性质发生了变化?
(师生一起):1、的图象可以看作把上所有的点的纵坐标伸长到原来的2倍(横坐标不变)而得到;
函数的值域变为了[-2,2]
2、的图象可以看作把上所有的点的纵坐标缩短到原来的倍(横坐标不变)而得到;
函数的值域变为了[]
『老师』再请大家思考:如果换成一般情况,你能归纳出它与 的联系吗?
(师生一起): 一般地,函数, (其A>0,且A1)的图象,可以看作是把正弦曲线上所有点的纵坐标伸长(当A>1时)或缩短(当0
在物理上,A称为振幅,我们把这种变换称为振幅变换。
说明:这要注意以下几点
1) 在变动中,变的是纵坐标,不变的是横坐标,伸长时A>1,缩短时0
例2.画出函数与的简图。
解:函数的周期为,我们先画在[0,]上的简图
令(换元法)
列表2: 描点连线:
0
0
0 1 0 -1 0
函数的周期为,我们先画在[0,4]上的简图
令,则(换元法)
列表3:
0
0
0 1 0 -1 0
同理,利用它们的周期性,把它们分别向左,右扩展得到它们在R上的简图。
『老师』大家思考一下:把它们与比较,有什么联系?其哪些性质发生了变化?
(师生一起):1、的图象可以看作把上所有的点的横坐标缩短到原来的倍(纵坐标不变)而得到;
函数的定义域、值域和奇偶性不变,周期变为原来的倍,单调区间也发生了改变。
2、的图象可以看作把上所有的点的横坐标伸长到原来的2倍(纵坐标不变)而得到;
函数的定义域、值域和奇偶性不变,周期变为原来的2倍,单调区间也发生了改变。
『老师』再请大家思考:如果换成一般情况,你能归纳出它与的联系吗?(学生先回答)
(师生一起): 一般地,函数, (其>0,且1)的图象,可以看作是把正弦曲线上所有点的横坐标伸长(当0<<1时)或缩短(当>1时)到原来的倍(纵坐标不变)而得到.
函数的中决定了其周期,所以我们把这一变换称为周期变换。
说明:1)列表时,x轴上的五个值怎样计算:换元法,解5个一元一次方程。
2)周期变换中,强调是“x轴上的所有点伸长或缩短”;“纵坐标不变”。
3)强调与振幅变换的区别:振幅变换是原来的A倍,周期变换是原来的。
例3.画出函数的简图。
解:函数的周期为,我们先画在[0,]上的简图
令(换元法)
列表4: 描点连线:
0
0
0 1 0 -1 0
0 3 0 3 0
『老师』大家思考一下:把它
与比较,有什么联
系?你可以试着由
的图象变换得到吗?
(学生思考)
『学生1』先把的
纵坐标伸长到原来的3倍(横坐标不变),得到,再把横坐标缩短到原来的倍(纵坐标不变),得到。
『学生2』先把的横坐标缩短到原来的倍(纵坐标不变),得到,再把纵坐标伸长到原来的3倍(横坐标不变),得到。
说明:启发引导学生自己的出结论,如果较困难,可以适当提醒。
三、课堂练习:
P73练习1、在坐标纸上作出下列函数在一个周期上的简图
(1) (2)
并说出它们可以由通过怎样的变换而得到?.
P74练习2、3(学生口答)
2、函数的振幅是多少?它的图象与正弦曲线有什么关系?
答案:振幅是,把正弦曲线上的纵坐标缩短到原来的倍,横坐标不变可得到它的图象。
3、函数的周期是什么?它的图象与正弦曲线有什么关系?
答案:振幅是,把正弦曲线上的横坐标伸长到原来的倍,纵坐标不变可得到它的图象。
四、课时小结:今天我们一起研究了形如的函数图象,它的图象可以通过的图象进行振幅变换和周期变换而得来,那么我们就要理解并学会对函数进行振幅变换;周期变换。
五、课后作业:1)预习课本P69例3;
2)习题4.9——P76:第二题——(1)(2)
3)目标训练二十六
4)复习函数的平移变换与今天的内容。
六、板书设计:
4.9.1 函数的图象(1)
复习:正弦、余弦函数的性质
新课: (振幅变换); (周期变换)
小结:
附1
附2
附3
附4
附5
附6
附7
附8
