沪科版八年级数学上册 13.1 三角形中的边角关系(第2课时) 教案
文档属性
| 名称 | 沪科版八年级数学上册 13.1 三角形中的边角关系(第2课时) 教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-07-31 18:19:53 | ||
图片预览

文档简介
第13章 三角形中的边角关系、命题与证明
13.1 三角形中的边角关系
第2课时 三角形中角的关系
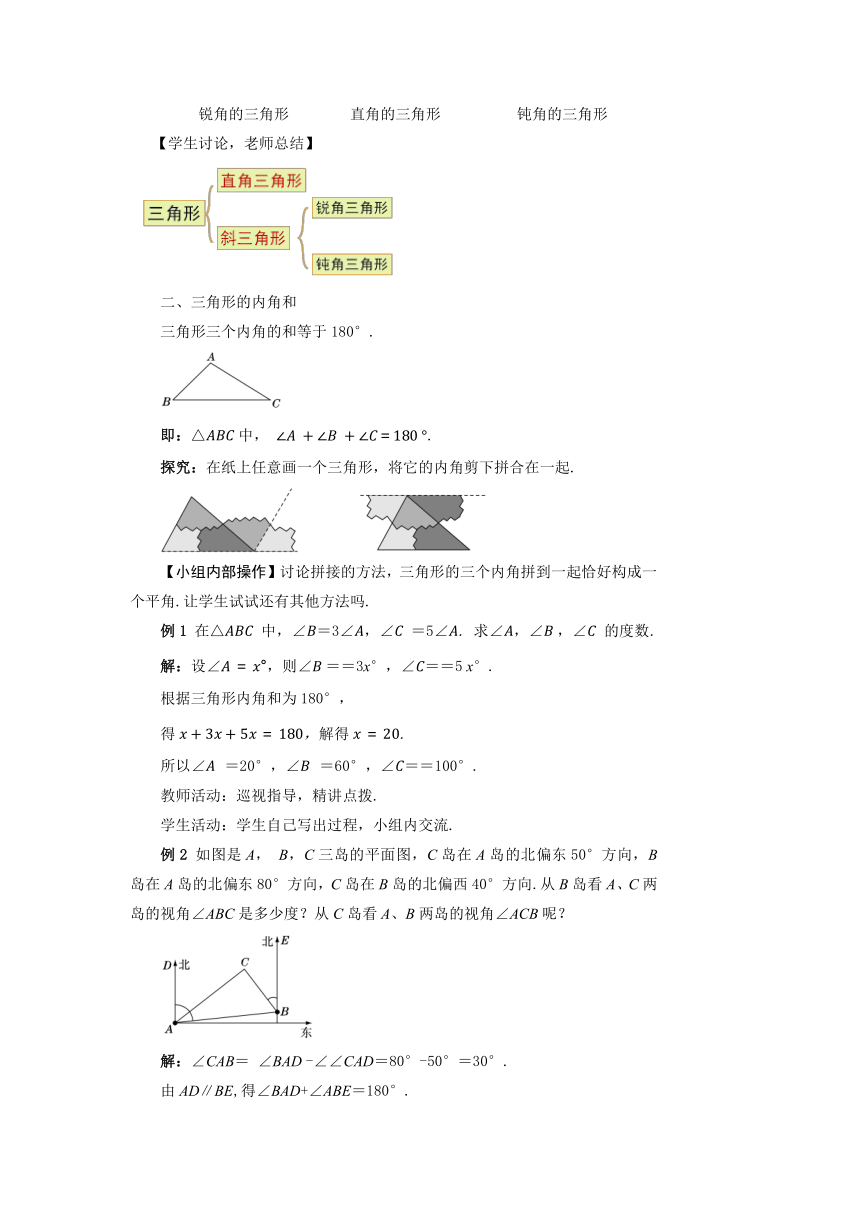
教学目标 1.引导学生按角的大小对三角形进行分类. 2.使学生掌握“三角形三个内角的和等于180°”,能应用三角形内角和解决一些简单的求三角形内角的度数问题. 3.引导学生通过观察、操作、想象“三角形三个内角的和等于180°”的活动过程,发展空间观念、推理能力和有条理的表达能力. 教学重难点 重点:按角的大小对三角形进行分类;三角形三个内角的和等于180°. 难点:探究、发现“三角形三个内角的和等于180°”. 教学过程 导入新课 一天,三角形界就三角形内角和的大小展开了一场激烈的争论,请同学们为它们评判一下吧. 探究新知 一、三角形按角的大小的分类 思考:按照三角形内角的大小,三角形可以分为哪几类? 锐角三角形 直角三角形 钝角三角形 ↑ ↑ ↑ 三个角都是 有一个角是 有一个角是 锐角的三角形 直角的三角形 钝角的三角形 【学生讨论,老师总结】 二、三角形的内角和 三角形三个内角的和等于180°. 即:△中, . 探究:在纸上任意画一个三角形,将它的内角剪下拼合在一起. 【小组内部操作】讨论拼接的方法,三角形的三个内角拼到一起恰好构成一个平角.让学生试试还有其他方法吗. 例1 在△ 中,∠=3∠,∠ =5∠. 求∠,∠,∠ 的度数. 解:设∠,则∠==3x°,∠==5 x°. 根据三角形内角和为180°, 得,解得. 所以∠ =20°,∠ =60°,∠==100°. 教师活动:巡视指导,精讲点拨. 学生活动:学生自己写出过程,小组内交流. 例2 如图是A, B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向.从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB呢? 解:∠CAB= ∠BAD -∠∠CAD=80°-50°=30°. 由AD∥BE,得∠BAD+∠ABE=180°. 所以∠ABE=180°-∠ BAD=180°-80°=100°, 所以∠ABC= ∠ABE-∠EBC=100°-40°=60°. 在△ABC中,∠ACB=180°-∠ABC -∠CAB =180°-60°-30°=90°, 即从B岛看A、C两岛的视角∠ABC是60°, 从C岛看A、B两岛的视角∠ACB是90°. 教师活动:巡视指导,精讲点拨. 学生活动:学生自己写出过程,小组内交流. 课堂练习 1.一个三角形的三个内角的度数之比为1∶2∶3,这个三角形一定是( ) A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法判定 2.如图,已知直线AB∥CD,∠C=115°,∠A=25°,则∠E=( ) A.70° B. 80° C. 90° D. 100° 3.(1)在△ABC中,∠A=35°,∠B=43°,则∠C =_______; (2)在△ABC中, ∠A=40°,∠A=2∠B,则∠C = ________. 4.已知,如图,D是△ABC中BC边延长线上一点,F为AB上一点,直线FD交AC于E,∠DFB=90°,∠A=46°,∠D=50°.求∠ACB的度数. 5. 探究与发现:如图1,有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.请写出∠BDC与∠A+∠ABD+∠ACD之间的数量关系,并说明理由. 应用:某零件如图2所示,图纸要求∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=145°时,就断定这个零件不合格,你能说出其中的道理吗? 图1 图2 参考答案 1.A 2.C 3.(1)102° (2)120° 4.解:在△DFB中, ∵∠DFB=90°,∠D=50°, ∠DFB+∠D+∠B=180°, ∴∠B=40°. 在△ABC中,∵∠A=46°,∠B=40°, ∴∠ACB=180°-∠A-∠B=94°. 5.解:探究与发现:∠BDC=∠A+∠ABD+∠ACD. 理由如下: 因为∠BDC+∠DBC+∠DCB=180°, ∠A+∠ABC+∠ACB=∠A+∠ABD+∠ACD+∠DBC+∠DCB=180°, 所以∠BDC=∠A+∠ABD+∠ACD. 应用:能,连接BC. 因为∠A=90°,∠ABD=32°,∠ACD=21°, 所以由上述结论,得∠BDC=∠A+∠ABD+∠ACD=143°. 因为检验员量得∠BDC=145°≠143°,所以这个零件不合格. 课堂小结 1. 2.三角形内角和等于180° 布置作业 P71练习 板书设计 三角形中角的关系 1.三角形按角分类 三角形 2.三角形内角和等于180°
13.1 三角形中的边角关系
第2课时 三角形中角的关系
教学目标 1.引导学生按角的大小对三角形进行分类. 2.使学生掌握“三角形三个内角的和等于180°”,能应用三角形内角和解决一些简单的求三角形内角的度数问题. 3.引导学生通过观察、操作、想象“三角形三个内角的和等于180°”的活动过程,发展空间观念、推理能力和有条理的表达能力. 教学重难点 重点:按角的大小对三角形进行分类;三角形三个内角的和等于180°. 难点:探究、发现“三角形三个内角的和等于180°”. 教学过程 导入新课 一天,三角形界就三角形内角和的大小展开了一场激烈的争论,请同学们为它们评判一下吧. 探究新知 一、三角形按角的大小的分类 思考:按照三角形内角的大小,三角形可以分为哪几类? 锐角三角形 直角三角形 钝角三角形 ↑ ↑ ↑ 三个角都是 有一个角是 有一个角是 锐角的三角形 直角的三角形 钝角的三角形 【学生讨论,老师总结】 二、三角形的内角和 三角形三个内角的和等于180°. 即:△中, . 探究:在纸上任意画一个三角形,将它的内角剪下拼合在一起. 【小组内部操作】讨论拼接的方法,三角形的三个内角拼到一起恰好构成一个平角.让学生试试还有其他方法吗. 例1 在△ 中,∠=3∠,∠ =5∠. 求∠,∠,∠ 的度数. 解:设∠,则∠==3x°,∠==5 x°. 根据三角形内角和为180°, 得,解得. 所以∠ =20°,∠ =60°,∠==100°. 教师活动:巡视指导,精讲点拨. 学生活动:学生自己写出过程,小组内交流. 例2 如图是A, B,C三岛的平面图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西40°方向.从B岛看A、C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB呢? 解:∠CAB= ∠BAD -∠∠CAD=80°-50°=30°. 由AD∥BE,得∠BAD+∠ABE=180°. 所以∠ABE=180°-∠ BAD=180°-80°=100°, 所以∠ABC= ∠ABE-∠EBC=100°-40°=60°. 在△ABC中,∠ACB=180°-∠ABC -∠CAB =180°-60°-30°=90°, 即从B岛看A、C两岛的视角∠ABC是60°, 从C岛看A、B两岛的视角∠ACB是90°. 教师活动:巡视指导,精讲点拨. 学生活动:学生自己写出过程,小组内交流. 课堂练习 1.一个三角形的三个内角的度数之比为1∶2∶3,这个三角形一定是( ) A.直角三角形 B.锐角三角形 C.钝角三角形 D.无法判定 2.如图,已知直线AB∥CD,∠C=115°,∠A=25°,则∠E=( ) A.70° B. 80° C. 90° D. 100° 3.(1)在△ABC中,∠A=35°,∠B=43°,则∠C =_______; (2)在△ABC中, ∠A=40°,∠A=2∠B,则∠C = ________. 4.已知,如图,D是△ABC中BC边延长线上一点,F为AB上一点,直线FD交AC于E,∠DFB=90°,∠A=46°,∠D=50°.求∠ACB的度数. 5. 探究与发现:如图1,有一块直角三角板DEF放置在△ABC上,三角板DEF的两条直角边DE、DF恰好分别经过点B、C.请写出∠BDC与∠A+∠ABD+∠ACD之间的数量关系,并说明理由. 应用:某零件如图2所示,图纸要求∠A=90°,∠B=32°,∠C=21°,当检验员量得∠BDC=145°时,就断定这个零件不合格,你能说出其中的道理吗? 图1 图2 参考答案 1.A 2.C 3.(1)102° (2)120° 4.解:在△DFB中, ∵∠DFB=90°,∠D=50°, ∠DFB+∠D+∠B=180°, ∴∠B=40°. 在△ABC中,∵∠A=46°,∠B=40°, ∴∠ACB=180°-∠A-∠B=94°. 5.解:探究与发现:∠BDC=∠A+∠ABD+∠ACD. 理由如下: 因为∠BDC+∠DBC+∠DCB=180°, ∠A+∠ABC+∠ACB=∠A+∠ABD+∠ACD+∠DBC+∠DCB=180°, 所以∠BDC=∠A+∠ABD+∠ACD. 应用:能,连接BC. 因为∠A=90°,∠ABD=32°,∠ACD=21°, 所以由上述结论,得∠BDC=∠A+∠ABD+∠ACD=143°. 因为检验员量得∠BDC=145°≠143°,所以这个零件不合格. 课堂小结 1. 2.三角形内角和等于180° 布置作业 P71练习 板书设计 三角形中角的关系 1.三角形按角分类 三角形 2.三角形内角和等于180°
