简单线性规划[上学期]
图片预览






文档简介
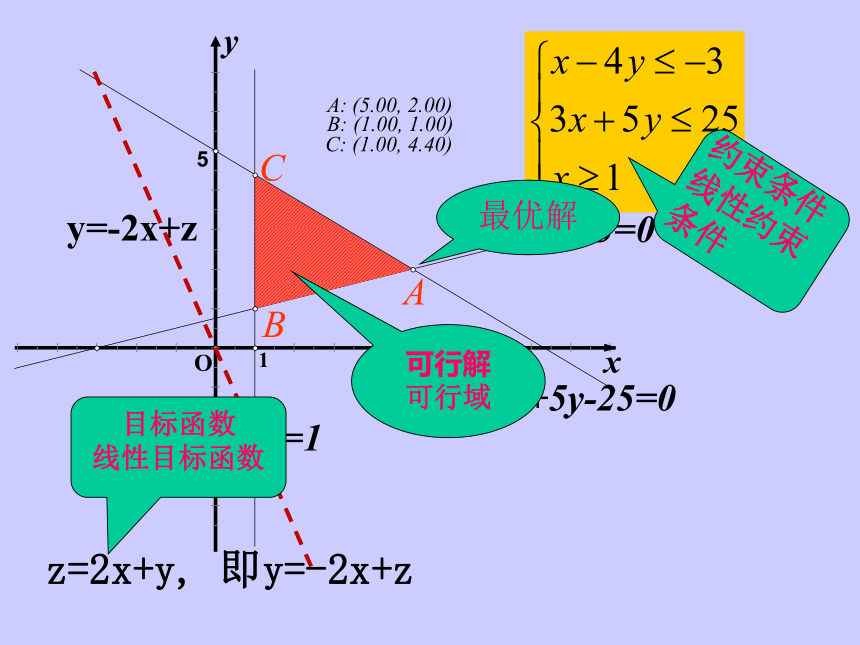
课件19张PPT。简单线性规划的应用 已知:(2)求z=2x+y的最大值引入练习:(1)画出不等式组所表示的平面区域.yy=-2x+zz=2x+y, 即y=-2x+z最优解目标函数
线性目标函数可行解
可行域
解线性规划问题的步骤: (1)画:画出线性约束条件所表示的可行域;(2)移:在线性目标函数所表示的一组平行 线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线; (3)求:通过解方程组求出最优解; (4)答:作出答案。 依题意,画区域,再把直线来平移,寻找最优在哪里.
在生产实际中有许多问题都可以化归为线性规划的问题,实际问题的应用 某家具厂有方木料900m3,五合板600m2,
准备加工成书桌和书橱出售,已知生产每张
书桌需要方木料0.1m3、五合板2m2,生产每
张书橱需要方木料0.2m3、五合板1m2,出售
一张书桌可获利润80元,出售一张书橱可获
利120元,如果只安排生产书桌,可获利润多
少?如果只安排生产书橱,可获利润多少?怎
样安排生产可使所得利润最大?研究一个例题: 某家具厂有方木料900m3,五合板600m2,准备加工成书桌和书橱出售,已知生产每张书桌需要方木料0.1m3、五合板2m2,生产每张书橱需要方木料0.2m3、五合板1m2,出售一张书桌可获利润80元,出售一张书橱可获利120元,如果只安排生产书桌,可获利润多少?如果只安排生产书橱,可获利润多少?怎样安排生产可使所得利润最大?讨论、思考:
1、设置适当的变量表示利润.
2、用表格的形式把已知量梳理清楚.
4、列出变量所受的约束条件.
3、利用所学知识尝试求解. 某家具厂有方木料900m3,五合板600m2,准备加工成书桌和书橱出售,已知生产每张书桌需要方木料0.1m3、五合板2m2,生产每张书橱需要方木料0.2m3、五合板1m2,出售一张书桌可获利润80元,出售一张书橱可获利120元,如果只安排生产书桌,可获利润多少?如果只安排生产书橱,可获利润多少?怎样安排生产可使所得利润最大?60012五合板(m2)9000.20.1方木料(m3)材料限额书橱(张)书桌(张) 产品
材料 60012五合板(m2)9000.20.1方木料(m3)材料限额书橱(张)书桌(张) 产品
材料 目标函数:最多只生产600张书橱,获利Z=72000元60012五合板(m2)9000.20.1方木料(m3)材料限额书橱(张)书桌(张) 产品
材料 600目标函数:2x+3y=0最优解为x=0,y=600最大利润Z=7200讨论:为什么会出现只生产书橱,可获最大利润呢?是否可以根据题目中的数据,做一定性分析? 某家具厂有方木料900m3,五合板600m2,准备加工成书桌和书橱出售,已知生产每张书桌需要方木料0.1m3、五合板2m2,生产每张书橱需要方木料0.2m3、五合板1m2,出售一张书桌可获利润80元,出售一张书橱可获利120元,如果只安排生产书桌,可获利润多少?如果只安排生产书橱,可获利润多少?怎样安排生产可使所得利润最大?60012五合板(m2)900.20.1方木料(m3)材料限额书橱(张)书桌(张) 产品
材料 目标函数:90目标函数:最优解为
x=100,y=400最大利润
Z=56000(100,400)(1)设置相应变量
(2)确定目标函数
(3)列出全部约束条件
(4)利用图解法求解、作答小结解线性规划应用问题的一般步骤 :
某公司承担了每天至少搬运280t水泥的
任务,已知该公司有6辆A型卡车和B型卡车,
已知A型卡车每天每辆的运载量为30t,成本
费为0.6千元,B型卡车每天每辆的运载量为
40t,成本费为1千元。如果你是公司的经理,
为使公司所花的成本费最小,该如何安排公
司每天的车辆。
练一练Z = 0.6x + yOyx(4,4)461 、星期天以活动小组为单位,到附近的工厂、乡镇企业、商店、学校等作调查研究,了解线性规划在实际中的应用,或提出能用线性规划的知识提高生产效率的实际问题,并作出解答。把实习和研究活动的成果写成实习报告、研究报告或小论文,并互相交流。课后作业返回作业
2、阅读P119例9、
P120例10
必做 P123 1、2、3
选做 P121 练习题
线性目标函数可行解
可行域
解线性规划问题的步骤: (1)画:画出线性约束条件所表示的可行域;(2)移:在线性目标函数所表示的一组平行 线中,利用平移的方法找出与可行域有公共点且纵截距最大或最小的直线; (3)求:通过解方程组求出最优解; (4)答:作出答案。 依题意,画区域,再把直线来平移,寻找最优在哪里.
在生产实际中有许多问题都可以化归为线性规划的问题,实际问题的应用 某家具厂有方木料900m3,五合板600m2,
准备加工成书桌和书橱出售,已知生产每张
书桌需要方木料0.1m3、五合板2m2,生产每
张书橱需要方木料0.2m3、五合板1m2,出售
一张书桌可获利润80元,出售一张书橱可获
利120元,如果只安排生产书桌,可获利润多
少?如果只安排生产书橱,可获利润多少?怎
样安排生产可使所得利润最大?研究一个例题: 某家具厂有方木料900m3,五合板600m2,准备加工成书桌和书橱出售,已知生产每张书桌需要方木料0.1m3、五合板2m2,生产每张书橱需要方木料0.2m3、五合板1m2,出售一张书桌可获利润80元,出售一张书橱可获利120元,如果只安排生产书桌,可获利润多少?如果只安排生产书橱,可获利润多少?怎样安排生产可使所得利润最大?讨论、思考:
1、设置适当的变量表示利润.
2、用表格的形式把已知量梳理清楚.
4、列出变量所受的约束条件.
3、利用所学知识尝试求解. 某家具厂有方木料900m3,五合板600m2,准备加工成书桌和书橱出售,已知生产每张书桌需要方木料0.1m3、五合板2m2,生产每张书橱需要方木料0.2m3、五合板1m2,出售一张书桌可获利润80元,出售一张书橱可获利120元,如果只安排生产书桌,可获利润多少?如果只安排生产书橱,可获利润多少?怎样安排生产可使所得利润最大?60012五合板(m2)9000.20.1方木料(m3)材料限额书橱(张)书桌(张) 产品
材料 60012五合板(m2)9000.20.1方木料(m3)材料限额书橱(张)书桌(张) 产品
材料 目标函数:最多只生产600张书橱,获利Z=72000元60012五合板(m2)9000.20.1方木料(m3)材料限额书橱(张)书桌(张) 产品
材料 600目标函数:2x+3y=0最优解为x=0,y=600最大利润Z=7200讨论:为什么会出现只生产书橱,可获最大利润呢?是否可以根据题目中的数据,做一定性分析? 某家具厂有方木料900m3,五合板600m2,准备加工成书桌和书橱出售,已知生产每张书桌需要方木料0.1m3、五合板2m2,生产每张书橱需要方木料0.2m3、五合板1m2,出售一张书桌可获利润80元,出售一张书橱可获利120元,如果只安排生产书桌,可获利润多少?如果只安排生产书橱,可获利润多少?怎样安排生产可使所得利润最大?60012五合板(m2)900.20.1方木料(m3)材料限额书橱(张)书桌(张) 产品
材料 目标函数:90目标函数:最优解为
x=100,y=400最大利润
Z=56000(100,400)(1)设置相应变量
(2)确定目标函数
(3)列出全部约束条件
(4)利用图解法求解、作答小结解线性规划应用问题的一般步骤 :
某公司承担了每天至少搬运280t水泥的
任务,已知该公司有6辆A型卡车和B型卡车,
已知A型卡车每天每辆的运载量为30t,成本
费为0.6千元,B型卡车每天每辆的运载量为
40t,成本费为1千元。如果你是公司的经理,
为使公司所花的成本费最小,该如何安排公
司每天的车辆。
练一练Z = 0.6x + yOyx(4,4)461 、星期天以活动小组为单位,到附近的工厂、乡镇企业、商店、学校等作调查研究,了解线性规划在实际中的应用,或提出能用线性规划的知识提高生产效率的实际问题,并作出解答。把实习和研究活动的成果写成实习报告、研究报告或小论文,并互相交流。课后作业返回作业
2、阅读P119例9、
P120例10
必做 P123 1、2、3
选做 P121 练习题
