【核心素养目标】24.4.2 圆锥的侧面积和全面积 学案
文档属性
| 名称 | 【核心素养目标】24.4.2 圆锥的侧面积和全面积 学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 06:02:27 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
24.4.2 圆锥的侧面积和全面积 导学案
课题 24.4.2 圆锥的侧面积和全面积 单元 第24单元 学科 数学 年级 九年级(上)
教材分析 通过实物演示让学生知道圆锥的侧面展开图是扇形;知道圆锥各部分的名称,能够计算圆锥的侧面积和全面积.
核心素养分析 通过展开圆锥知道圆锥的全面积是扇形和底面圆形,通过制作圆锥,理解圆锥与扇形和圆之间的关系,进一步体会数学中的转化思想,培养学生动手操作能力和分析问题解决问题的能力.
学习目标 1.了解圆锥的母线定义,理解圆锥的侧面展开图是一个扇形;2.熟练掌握圆锥的侧面积和全面积公式,并能解决相关计算问题.
重点 计算圆锥的侧面积和全面积.
难点 圆锥侧面展开的扇形和底面圆之间有关元素的计算.
教学过程
课前预学 引入思考大家见过圆锥吗?你能举出实例吗?你们知道圆锥的表面是由哪些面构成的吗?请大家互相交流.环节一:探究圆锥侧面展开图①圆锥:是由一个底面和一个侧面围成的几何体,如图,②母线:我们把连接圆锥______和底面______任意一点的线段叫做圆锥的母线.③高:连结______与底面______的线段叫做圆锥的高.通过你的认识,从图形中你知道半径、高线、 母线长三者之间的关系吗? 环节二:探究圆锥侧面积和全面积公式思考:1.圆锥的表面是由哪些面构成的?2.圆锥的侧面展开图是什么图形?3.如何计算圆锥的侧面积?4.如何计算圆锥的全面积?
新知讲解 提炼概念强调:(1)圆锥和侧面展开图之间的联系 ;(2)圆锥的高、底面圆的半径、母线长三者之间的数量关系。典例精讲 例1、蒙古包可以近似地看作由圆锥和圆柱组成.如果想用毛毡搭建20个底面积为12 m2,高为3.2 m,外围高1.8 m的蒙古包,至少需要多少平方米的毛毡(n取3.142,结果取整数)? 思考:你能探究展开图中的圆心角n与r、l之间的关系吗?
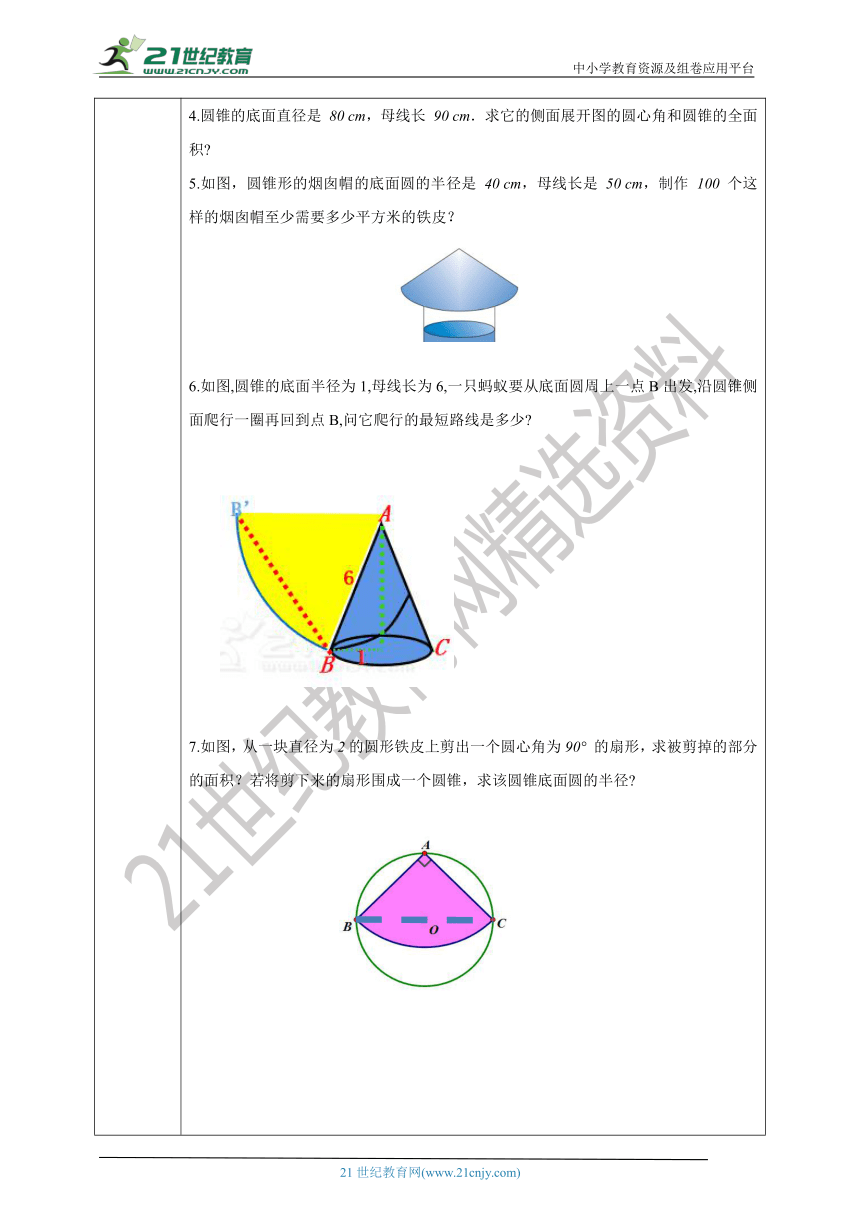
课堂练习 巩固训练 1. 已知圆锥的底面面积为4πcm2,母线长为7cm,则圆锥的侧面积是( ) A. 28πcm2 B. 14πcm2 C. 9πcm2 D. 6πcm22. 已知圆锥的底面半径为6cm,高为8cm,则圆锥的全面积是( ) A. 48πcm2 B. 84πcm2 C. 96πcm2 D. 144πcm23. 已知一直角三角形的三边分别为3、4、5,分别以( )条边所在直线为轴旋转一周所得几何体的表面积最大.A.3 B.4 C.5 D. 不确定4.圆锥的底面直径是 80 cm,母线长 90 cm.求它的侧面展开图的圆心角和圆锥的全面积 5.如图,圆锥形的烟囱帽的底面圆的半径是 40 cm,母线长是 50 cm,制作 100 个这样的烟囱帽至少需要多少平方米的铁皮?6.如图,圆锥的底面半径为1,母线长为6,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬行一圈再回到点B,问它爬行的最短路线是多少 7.如图,从一块直径为2的圆形铁皮上剪出一个圆心角为90° 的扇形,求被剪掉的部分的面积?若将剪下来的扇形围成一个圆锥,求该圆锥底面圆的半径 答案引入思考环节一:探究圆锥侧面展开图①圆锥:是由一个底面和一个侧面围成的几何体,如图,②母线:我们把连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.③高:连结顶点与底面圆心的线段叫做圆锥的高.通过你的认识,从图形中你知道半径、高线、 母线长三者之间的关系吗?圆锥的底面半径、高线、 母线长三者之间的关系:环节二:探究圆锥侧面积和全面积公式思考:1.圆锥的表面是由哪些面构成的?圆面和曲面2.圆锥的侧面展开图是什么图形?如图,沿一条母线将圆锥侧面剪开并展平,容易得到,圆锥的侧面展开图是一个扇形.3.如何计算圆锥的侧面积?设圆锥的母线长为l,底面圆的半径为r,那么这个扇形的半径为l,扇形的弧长为2πr,因此圆锥的侧面积为πrl4.如何计算圆锥的全面积?全面积等于底面积+侧面积,即圆锥的全面积为πr(r+l).提炼概念 典例精讲 例3 解: 根据题意,下部圆柱的底面积为 12 m2,高 h2 = 1.8 m;上部圆锥的高 h1 = 3.2-1.8 = 1.4 ( m ).圆柱的底面圆的半径圆柱侧面积为圆锥的母线长圆锥的侧面积因此,搭建 1个这样的蒙古包至少需要毛毡搭建 20 个这样的蒙古包至少需要毛毡答:搭建 20 个这样的蒙古包至少需要738平米的毛毡。巩固训练B2.C 3.A 4.解:∵ 圆锥的底面直径是 80 cm, ∴ 圆锥的底面半径 r=40cm , ∴ 圆锥的底面圆的周长C=80πcm ∵ 母线长 90 cm,∴ 圆心角 n=160° .∴ 圆锥的全面积为5.解:由题意知:r=40cm,l=50cm∴ 圆锥的侧面积为答:制作 100 个这样的烟囱帽至少需要20πm2的铁皮.6.7.解:∵剪出的扇形的圆心角为90° ∴BC过圆心O,即BC=2∴扇形的半径为AB=AC= 答:被剪掉的部分的面积为 ,圆锥底面圆的半径是 .
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
24.4.2 圆锥的侧面积和全面积 导学案
课题 24.4.2 圆锥的侧面积和全面积 单元 第24单元 学科 数学 年级 九年级(上)
教材分析 通过实物演示让学生知道圆锥的侧面展开图是扇形;知道圆锥各部分的名称,能够计算圆锥的侧面积和全面积.
核心素养分析 通过展开圆锥知道圆锥的全面积是扇形和底面圆形,通过制作圆锥,理解圆锥与扇形和圆之间的关系,进一步体会数学中的转化思想,培养学生动手操作能力和分析问题解决问题的能力.
学习目标 1.了解圆锥的母线定义,理解圆锥的侧面展开图是一个扇形;2.熟练掌握圆锥的侧面积和全面积公式,并能解决相关计算问题.
重点 计算圆锥的侧面积和全面积.
难点 圆锥侧面展开的扇形和底面圆之间有关元素的计算.
教学过程
课前预学 引入思考大家见过圆锥吗?你能举出实例吗?你们知道圆锥的表面是由哪些面构成的吗?请大家互相交流.环节一:探究圆锥侧面展开图①圆锥:是由一个底面和一个侧面围成的几何体,如图,②母线:我们把连接圆锥______和底面______任意一点的线段叫做圆锥的母线.③高:连结______与底面______的线段叫做圆锥的高.通过你的认识,从图形中你知道半径、高线、 母线长三者之间的关系吗? 环节二:探究圆锥侧面积和全面积公式思考:1.圆锥的表面是由哪些面构成的?2.圆锥的侧面展开图是什么图形?3.如何计算圆锥的侧面积?4.如何计算圆锥的全面积?
新知讲解 提炼概念强调:(1)圆锥和侧面展开图之间的联系 ;(2)圆锥的高、底面圆的半径、母线长三者之间的数量关系。典例精讲 例1、蒙古包可以近似地看作由圆锥和圆柱组成.如果想用毛毡搭建20个底面积为12 m2,高为3.2 m,外围高1.8 m的蒙古包,至少需要多少平方米的毛毡(n取3.142,结果取整数)? 思考:你能探究展开图中的圆心角n与r、l之间的关系吗?
课堂练习 巩固训练 1. 已知圆锥的底面面积为4πcm2,母线长为7cm,则圆锥的侧面积是( ) A. 28πcm2 B. 14πcm2 C. 9πcm2 D. 6πcm22. 已知圆锥的底面半径为6cm,高为8cm,则圆锥的全面积是( ) A. 48πcm2 B. 84πcm2 C. 96πcm2 D. 144πcm23. 已知一直角三角形的三边分别为3、4、5,分别以( )条边所在直线为轴旋转一周所得几何体的表面积最大.A.3 B.4 C.5 D. 不确定4.圆锥的底面直径是 80 cm,母线长 90 cm.求它的侧面展开图的圆心角和圆锥的全面积 5.如图,圆锥形的烟囱帽的底面圆的半径是 40 cm,母线长是 50 cm,制作 100 个这样的烟囱帽至少需要多少平方米的铁皮?6.如图,圆锥的底面半径为1,母线长为6,一只蚂蚁要从底面圆周上一点B出发,沿圆锥侧面爬行一圈再回到点B,问它爬行的最短路线是多少 7.如图,从一块直径为2的圆形铁皮上剪出一个圆心角为90° 的扇形,求被剪掉的部分的面积?若将剪下来的扇形围成一个圆锥,求该圆锥底面圆的半径 答案引入思考环节一:探究圆锥侧面展开图①圆锥:是由一个底面和一个侧面围成的几何体,如图,②母线:我们把连接圆锥顶点和底面圆周上任意一点的线段叫做圆锥的母线.③高:连结顶点与底面圆心的线段叫做圆锥的高.通过你的认识,从图形中你知道半径、高线、 母线长三者之间的关系吗?圆锥的底面半径、高线、 母线长三者之间的关系:环节二:探究圆锥侧面积和全面积公式思考:1.圆锥的表面是由哪些面构成的?圆面和曲面2.圆锥的侧面展开图是什么图形?如图,沿一条母线将圆锥侧面剪开并展平,容易得到,圆锥的侧面展开图是一个扇形.3.如何计算圆锥的侧面积?设圆锥的母线长为l,底面圆的半径为r,那么这个扇形的半径为l,扇形的弧长为2πr,因此圆锥的侧面积为πrl4.如何计算圆锥的全面积?全面积等于底面积+侧面积,即圆锥的全面积为πr(r+l).提炼概念 典例精讲 例3 解: 根据题意,下部圆柱的底面积为 12 m2,高 h2 = 1.8 m;上部圆锥的高 h1 = 3.2-1.8 = 1.4 ( m ).圆柱的底面圆的半径圆柱侧面积为圆锥的母线长圆锥的侧面积因此,搭建 1个这样的蒙古包至少需要毛毡搭建 20 个这样的蒙古包至少需要毛毡答:搭建 20 个这样的蒙古包至少需要738平米的毛毡。巩固训练B2.C 3.A 4.解:∵ 圆锥的底面直径是 80 cm, ∴ 圆锥的底面半径 r=40cm , ∴ 圆锥的底面圆的周长C=80πcm ∵ 母线长 90 cm,∴ 圆心角 n=160° .∴ 圆锥的全面积为5.解:由题意知:r=40cm,l=50cm∴ 圆锥的侧面积为答:制作 100 个这样的烟囱帽至少需要20πm2的铁皮.6.7.解:∵剪出的扇形的圆心角为90° ∴BC过圆心O,即BC=2∴扇形的半径为AB=AC= 答:被剪掉的部分的面积为 ,圆锥底面圆的半径是 .
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
同课章节目录
