对数函数的综合运用[上学期]

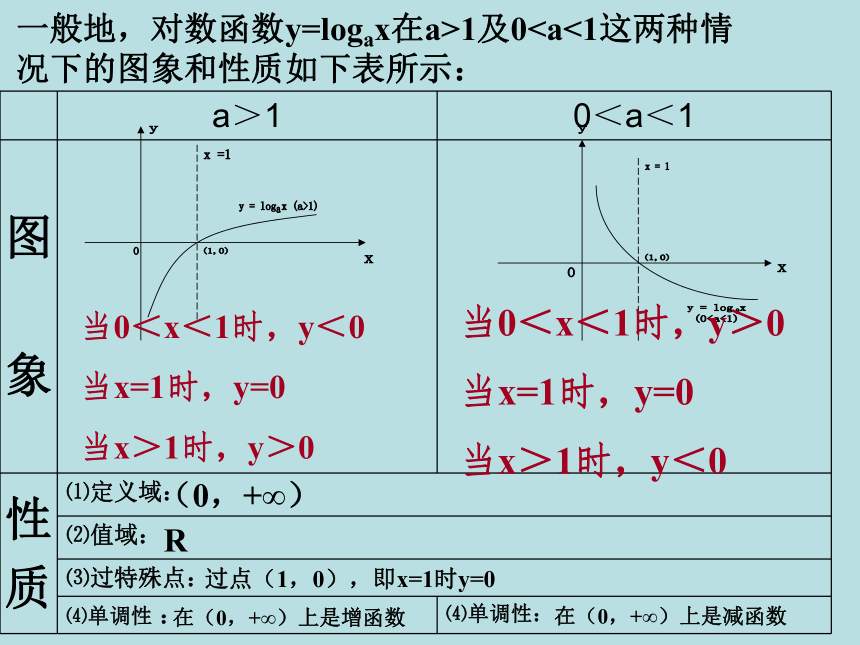
课件12张PPT。指数函数性质的综合应用深圳清华实验学校 龙其越一般地，对数函数y=logax在a>1及0当x=1时，y=0
当x＞1时，y＞0当0＜x＜1时，y＞0
当x=1时，y=0
当x＞1时，y＜01.函数单调性的应用举例
(1)比较大小. (2)解不等式.知识要求 2.方法:①底数相同的对数直接利用单调性.
②底数不同用“搭桥法”即引用“中间量”.小结：（二）新课讲解
例1．求下列函数的值域： 对于y=logaf(x)的值域的求法：（１）先求函数的定义域;
（２ ）确定f(x)的值域;　
（３）利用对数函数的单调性 ,
求出函数的值域
１.定义法：常用作差法比较．２.利用复合函数y=f[g(x)]的单调性规律判断　f(u)与g(x)若具有相同的单调性则f[g(x)]必定是增函数;
　f(u)与g(x)若具有不同的单调性则f[g(x)]必定是减函数
函数单调性的判断一般采用哪些方法？例３.若函数y=–log2(x2 –2ax +a)
在区间(–∞?, –1)上是增函数，
求a的取值范围．1.复合函数问题的解决关键在于将复合函数为题转化为简单基本函数问题，要注意等价性。研究函数的单调性在其定义域内讨论。
2.对于y=log a f(x)函数要确保f(x)>0，当a>1时y=log a f(x)的单调性在f(x)>0的前提下与y=f(x)的单调性一致。
当00的前提下与y=f(x)的单调性相反.(四）小结：