对数函数性质的综合应用[上学期]

课件12张PPT。对数函数性质的综合应用对数函数性质的综合应用
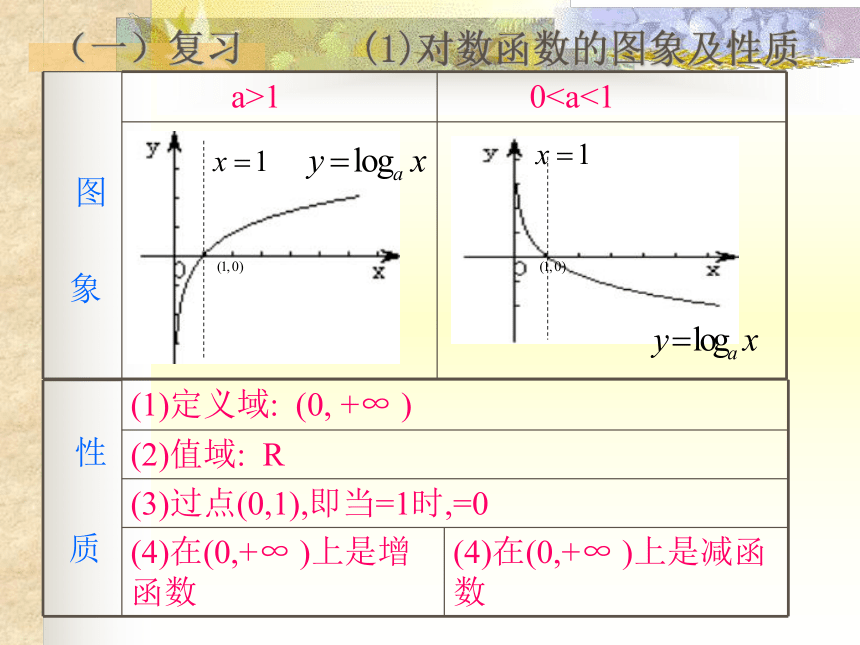
深圳清华实验学校 龙其越（一）复习 (1)对数函数的图象及性质 2.比较下列各组数中两个值的大小 （1）1.10.9, log1.10.9, log0.70.8
（2）log53, log63, log73解:(1) ∵ 1.10.9>1.10=1,
log1.10.9 0=log0.71 ∴ 1.10.9>log0.70.8>log1.10.9
(2)∵0 ∴log53>log63>log73
（二）新课讲解
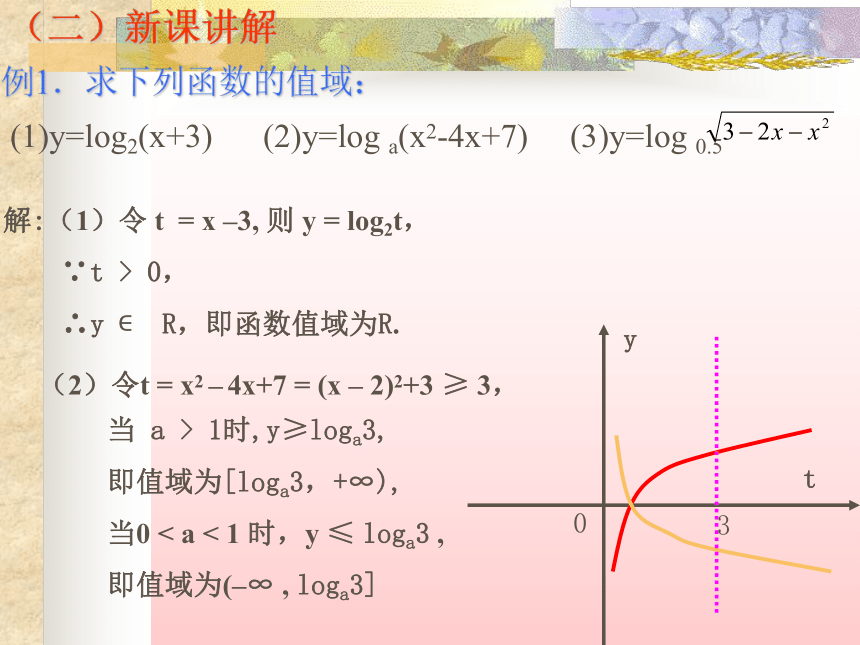
例1．求下列函数的值域： (1)y=log2(x+3) (2)y=log a(x2-4x+7) (3)y=log 0.5解:（1）令 t = x –3, 则 y = log2t，
∵t > 0，
∴y ? R，即函数值域为R.

（2）令t = x2 – 4x+7 = (x – 2)2+3 ≥ 3，
0ty当 a > 1时,y≥loga3,
即值域为[loga3，+∞),
当0 < a < 1 时，y ≤ loga3 ,
即值域为(–∞ , loga3]
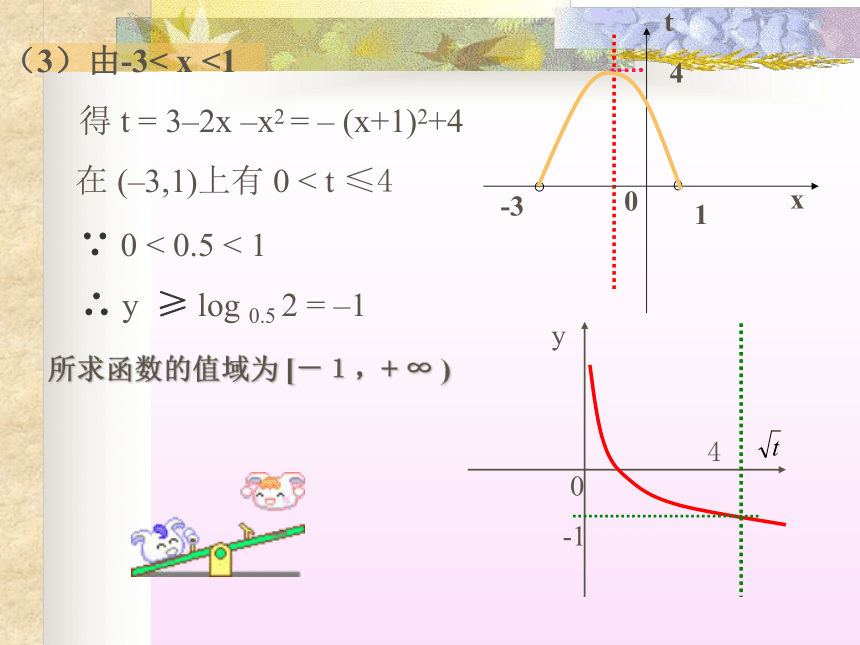
3（3）由-3< x <1
得 t = 3–2x –x2 = – (x+1)2+4
在 (–3,1)上有 0 < t ≤4 所求函数的值域为 [－１，+ ∞ )
∵ 0 < 0.5 < 1
∴ y ≥ log 0.5 2 = –14对于y=logaf(x)的值域的求法：（１）先求函数的定义域;
（２ ）确定f(x)的值域;　
（３）利用对数函数的单调性 ,
求出函数的值域
例２.求函数y=log0.3(x2-4x+3)的单调区间解： ∵ x2 – 4x + 3> 0 ∴x>3 或 x<1
令u=x2 – 4x + 3=(x –2)2 –1
在（–∞，２）上递增，
在（２，+∞?）上递减．
又∵ x>3 或 x<1，
∴ u=x2 – 4x + 3在（–∞，１）上递增
在（３，+∞?）上递减．
又∵y=log0.3u为减函数
∴函数y=log 0.3 (x2 - 4x+3 )在（–∞，１）上递减,在 （３，+∞?）上递增．
１.定义法：常用作差法比较．２.利用复合函数y=f[g(x)]的单调性规律判断　f(u)与g(x)若具有相同的单调性则f[g(x)]必定是增函数;
　f(u)与g(x)若具有不同的单调性则f[g(x)]必定是减函数
函数单调性的判断一般采用哪些方法？例３.若函数y=–log2(x2 –2ax +a)在区间(–∞?, –1)上是增函数，求a的取值范围．　解：令u=g(x)= x2 –2ax +a,
　　　　∵?函数y=–log2u为减函数
　　　　　　　　　　∴?u=g(x)= x2 –2ax +a在区间(–∞?, –1),
且满足u>0,
∴　　a ≥ –1
　　　　g(–1) ≥0
逆用解得：–1≤?a ≤１
所以a的取值范围为[–1,1](三）课堂练习１.函数y= lg –x2+2x+9 的定义域是
值域是
２.函数y=log0.5(x2–4x)的值域是
单调增区间是
３.若函数y=loga(2–ax)在[0,1]上是减函数,a的取 值范围是 [2，4][0，1]（–∞，0）（–∞，0）1＜a＜21.复合函数问题的解决关键在于将复合函数为题转化为简单基本函数问题，要注意等价性。研究函数的单调性在其定义域内讨论。
2.对于y=log a f(x)函数要确保f(x)>0，当a>1时y=log a f(x)的单调性在f(x)>0的前提下与y=f(x)的单调性一致。
当00的前提下与y=f(x)的单调性相反.(四）小结：(五）作业