用二分法求方程的近似解[上学期]
图片预览




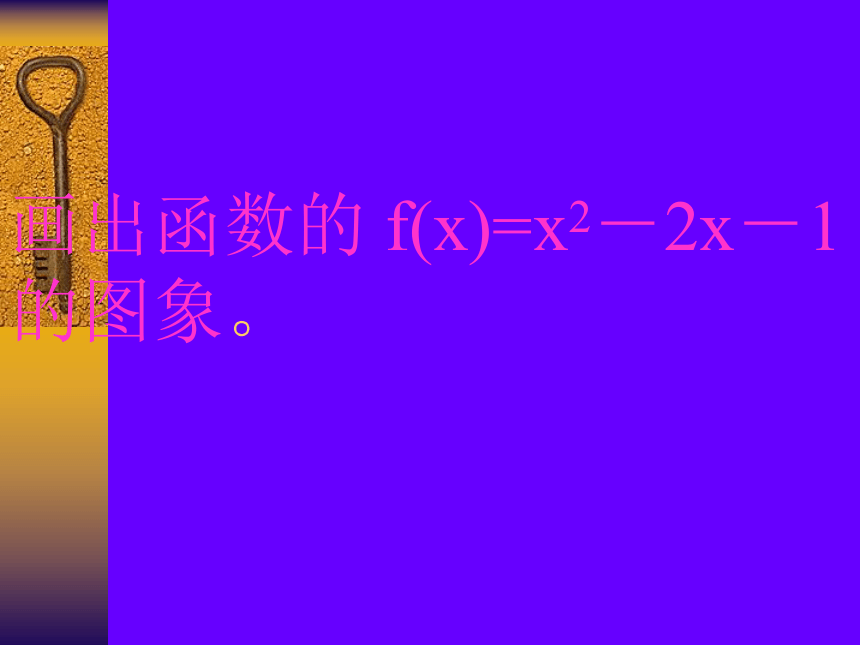



文档简介
课件25张PPT。用二分法求方程的近似解高一数学备课组教学目标: (1)理解运用二分法求方程近似解的方法 ; (2)能够借助计算器用二分法求相应方程的近似解 。
教学重点:
用二分法求相应方程的近似解 。
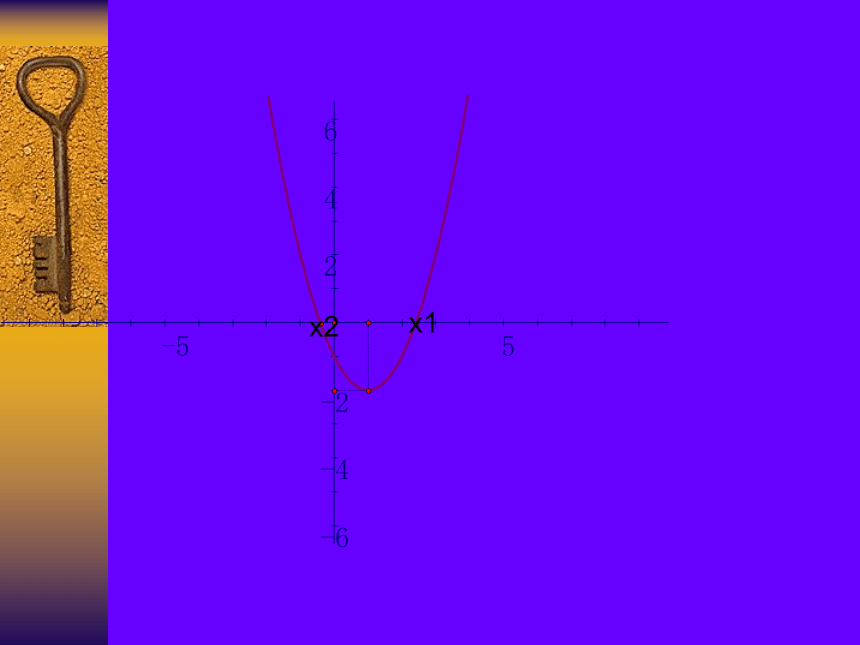
教学难点:对二分法的理解。 在CCTV2幸运52中,我们见过这样的片段“主持人说道:猜一猜这件的商品价格。观众:2000!主持人:高了!观众:1000!主持人:低了!观众:1700!主持人:高了!观众:1400!主持人:低了!观众:1500!主持人:低了!观众:1550!主持人:低了!观众:1580!主持人:高了!观众:1570!主持人:低了!观众:1578!主持人:低了!观众:1579!主持人:这件商品归你了。” 思考:如果让你来猜一件商品的价格,你如何猜? 画出函数的 f(x)=x2-2x-1的图象。如图所示642-2-4-6-55x1x2 从图象上可以发现,方程 x2-2x-1=0的一个根 x1在区间(2,3)内,另一个根x2在区间(-1,0)内。根据图象,我们发现f(2)=-1<0 ,f(3)=2>0,这表明此函数图象在区间(2,3)内穿过x轴一次,即方程f(x)=0在区间(2,3)上有惟一解。 计算 f((2+3)/2 )= 0.25>0,发现x1∈(2,2.5),这样可以进一步缩小 x1 所在的区间。
思考:如何把 x1限制在更小的区间内?例1 利用计算器,求方程x2-2x-1=0的一个近似解(精确到0.1)。
解 设f(x)=x2-2x-1,先画出函数图象的简图 因为f(2)=-1<0,f(3)=2>0, 所以 在区间(2,3)内,方程x2-2x-1=0有一解,记为x1。取2与3的平均数 2.5, 因为f(2.5)=0.25>0,所以2<x1<2.5再取2与2.5的平均数 2.25,因为f(2.25)=-0.4375<0 ,所以2.25<x1<2.5如此继续下去,得 f(2)<0,f(3)>0 x1∈(2,3) f(2)<0,f(2.5)>0 x1∈ (2,2.5) f(2.25)<0,f(2.5)>0 x1∈(2.25,2.5) f(2.375)<0,f(2.5)>0 x1∈(2.375,2.5) f(2.375)<0,f(2.4375)>0 x1∈(2.375,2.4375)
因为2.735与2.4375精确到0.1的近似值都为2.4,所以此方程的近似解为 x1≈2.4
利用同样的方法,还可以求出方程的另一个近似解。定义:对于在区间(a,b)上连续不间断,且f(a)f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法。用自己的语言叙述用二分法求方程近似值解的基本步骤。(1)取f(x)定义域内的一个闭区间[a,b],使得f(a)与f(b)异号,即f(a)f(b)<0,令a0=a,b0=b;(2)取区间[a0, b0]的中点x0=(a0+b0)/2,计算f(x0)和f(a0)并判断:①如果f(x0)=0,则x0就是方程的解,计算结束;②如果f(a0)f(x0)<0,则解位于区间[a0, x0]中,令a1=a0,b1=x0;③如果 f(a0)f(x0)>0则解位于区间[x0,b0]中,令a1=x0,b1=b0。 (3)取区间[a1,b1]的中点,则此中点对应的横坐标为x1=(a1+b1)/2,计算f(x1)和f(a1)并判断: ① 如果f(x1)=0则x1就是方程的解,计算结束;② 如果f(a1)f(x1)<0,则解位于区间[a1,x1]中,令a2=a1,b2=x1;③ 如果f(a1)f(x1)>0,则解位于区间[x1,b1]中,令a2=x1,b2=b1。
(4)重复上述步骤,可得方程的解总位于区间[an,bn]上,直至an和bn按指定精度取近似值时相等,那么这个近似值就是方程的一个近似解。练习 试判断方程x3+3x-1=0在区间(0,1)内是否有解。解 设x3+3x-1=0 , 则
因为 f(0)=03+3×0-1=-1 f(1)=13+3×1-1=3
所以 f(0) f(1) <0
故 方程 x3+3x-1=0在区间(0,1)内有解。例2 利用计算器,求方程lgx=3-x的近似解(精确到0.01).分析 分别画函数y=lgx和y=3-x的图象。在两个函数图象的交点处,函数值相等。因此,这个点的横坐标就是方程lgx=3-x的解。由图象还可以发现,方程有惟一解,记为x1,并且这个解在区间(2,3)内。
642-2-4-552y=3-xy=lgx134解 设f(x)=lgx+x-3,用计算器计算,得 f(2)<0,f(3)>0 x1(2,3) f(2.5)<0, f(3)>0 x1(2.5,3) f(2.5)<0, f(2.75)>0 x1(2.5,2.75) f(2.5)<0,f(2.625)>0 x1(2.5,2.625) f(2.5625)<0, f(2.625)>0 x1(2.5625,2.625). 因为2.5625与2.625精确到0.1的近似值都为2.6,所以原方程的近似解为 x1≈2.6注意: (1)曲线的交点坐标是方程组的解,最终转化为求方程的根。(2)求曲线y=f(x)和y=g(x)的交点的横坐标,实际上就是求函数y=f(x)-g(x)的零点,即求方程f(x)-g(x)=0的实数解。思考:将原方程写成x=3-lgx取x1=2,用计算器计算,则 3-lg2≈2.69897→x2再将x2=2.69897代人3-lgx2得x3,如此循环计算9次后,你发现了什么? 练习 用二分法求函数f(x)=x3-3的一个正实数零点(精确到0.01)解 由于f(1)=-2<0,f(2)=5>0,因此可取区间[1,2]作为计算的初始区间,用二分法逐步计算
f(1)=-2<0,f(1.5)=0.375>0
f(1.25)=-1.0469<0,f(1.5)=0.375>0
f(1.375)= -0.4004<0, f(1.5)=0.375>0
f(1.4375)= -0.0295<0, f(1.5)=0.375>0f(1.4375)=-0.0295<0,f(1.46875)=0.1684>0 f(1.4375)= -0.0295<0,f(1.463125)>0 f(1.4375)= -0.0295<0,f(1.4453125)>0∵1.4453125-1.4375=0.0078125<0.01,
∴x=(1.4453125+ 1.4375)/2≈1.44例3 在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发生了故障。这是一条10km长的线路,如何迅速查出故障所在?如果沿着线路一小段一小段查找,困难很多。每查一个点要爬一次电线杆子,10km长,大约有200多根电线杆子呢。 ???????想一想,维修线路的工人师傅怎样工作最合理? 解 可利用二分法的原理进行查找 如图,设闸门和指挥部的所在处为点A、B,他首先从中点C查。用随身带的话机向两端测试时,发现AC段正常,断定故障在BC段,再到BC段中点D,这次发现BD段正常,可见故障在CD段,再到CD段中点E来看。这样每查一次,就可以把待查的线路长度缩减一半,故经过7次查找,就可将故障发生的范围缩小到50—100m左右,即一两根电线杆附近。小结: 1、二分法的定义,它是一种求一元方程近似解的通法; 2、了解用二分法求解方程的一般步骤; 3、能够尝试对二分法进行编程,通过计算机来求方程的近似解。作业 1、用二分法求方程 在区间(3,4)内的一个近似解(精确到0.1); 2、利用计算器,求方程 的近似解(精确到0.1)。
642-2-4-552y=3-xy=lgx134解 设f(x)=lgx+x-3,用计算器计算,得 f(2)<0,f(3)>0 x1(2,3) f(2.5)<0, f(3)>0 x1(2.5,3) f(2.5)<0, f(2.75)>0 x1(2.5,2.75) f(2.5)<0,f(2.625)>0 x1(2.5,2.625) f(2.5625)<0, f(2.625)>0 x1(2.5625,2.625). 因为2.5625与2.625精确到0.1的近似值都为2.6,所以原方程的近似解为 x1≈2.6注意: (1)曲线的交点坐标是方程组的解,最终转化为求方程的根。(2)求曲线y=f(x)和y=g(x)的交点的横坐标,实际上就是求函数y=f(x)-g(x)的零点,即求方程f(x)-g(x)=0的实数解。思考:将原方程写成x=3-lgx取x1=2,用计算器计算,则 3-lg2≈2.69897→x2再将x2=2.69897代人3-lgx2得x3,如此循环计算9次后,你发现了什么? 练习 用二分法求函数f(x)=x3-3的一个正实数零点(精确到0.01)解 由于f(1)=-2<0,f(2)=5>0,因此可取区间[1,2]作为计算的初始区间,用二分法逐步计算
f(1)=-2<0,f(1.5)=0.375>0
f(1.25)=-1.0469<0,f(1.5)=0.375>0
f(1.375)= -0.4004<0, f(1.5)=0.375>0
f(1.4375)= -0.0295<0, f(1.5)=0.375>0f(1.4375)=-0.0295<0,f(1.46875)=0.1684>0 f(1.4375)= -0.0295<0,f(1.463125)>0 f(1.4375)= -0.0295<0,f(1.4453125)>0∵1.4453125-1.4375=0.0078125<0.01,
∴x=(1.4453125+ 1.4375)/2≈1.44例3 在一个风雨交加的夜里,从某水库闸房到防洪指挥部的电话线路发生了故障。这是一条10km长的线路,如何迅速查出故障所在?如果沿着线路一小段一小段查找,困难很多。每查一个点要爬一次电线杆子,10km长,大约有200多根电线杆子呢。 ???????想一想,维修线路的工人师傅怎样工作最合理? 解 可利用二分法的原理进行查找 如图,设闸门和指挥部的所在处为点A、B,他首先从中点C查。用随身带的话机向两端测试时,发现AC段正常,断定故障在BC段,再到BC段中点D,这次发现BD段正常,可见故障在CD段,再到CD段中点E来看。这样每查一次,就可以把待查的线路长度缩减一半,故经过7次查找,就可将故障发生的范围缩小到50—100m左右,即一两根电线杆附近。小结: 1、二分法的定义,它是一种求一元方程近似解的通法; 2、了解用二分法求解方程的一般步骤; 3、能够尝试对二分法进行编程,通过计算机来求方程的近似解。作业 1、用二分法求方程 在区间(3,4)内的一个近似解(精确到0.1); 2、利用计算器,求方程 的近似解(精确到0.1)。
