用二分法求方程的近似解[上学期]
图片预览





文档简介
课件17张PPT。这个游戏包含了什么样的数学思想:(2)体现了函数y=f(x)的零点和
方程f(x)=0的实数根之间的关系.(1)通过不断的缩小区间的长度,最后逼近实际的数值.练习:根据上述游戏的思想去计算出无理数 的一个近似值(精确到0.1).课题
用二分法求方程的近似解例1 利用计算器,二分法求方程
x2-2x-1=0的一个近似解.
(计算结果精确到0.1)分析:首先画出函数f(x)=x2-2x-1的图象,从图象上可以发现,方程
x2-2x-1=0的一个根x1
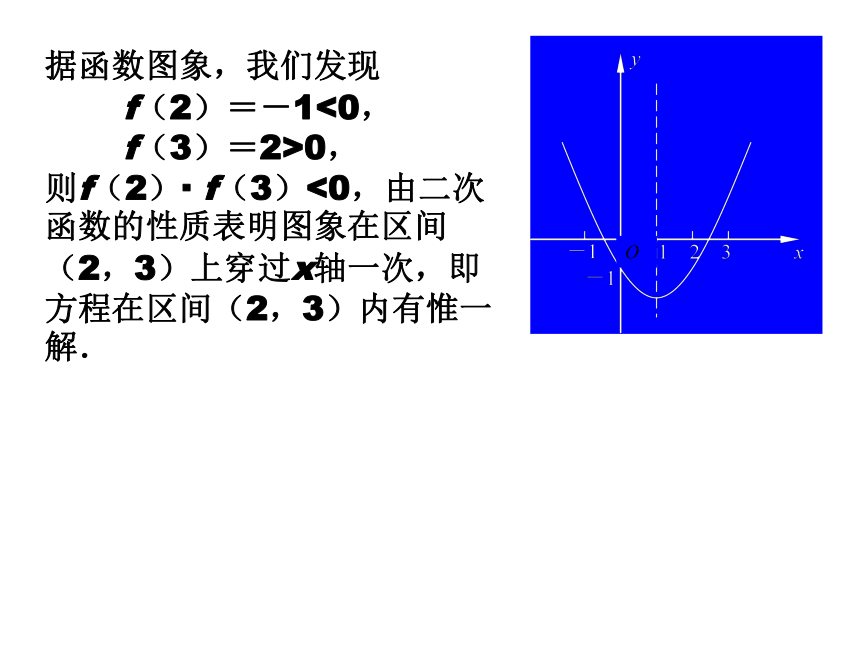
在区间(-1,0)内,另一个根x2在区间(2,3)内.据函数图象,我们发现
f(2)=-1<0,
f(3)=2>0,
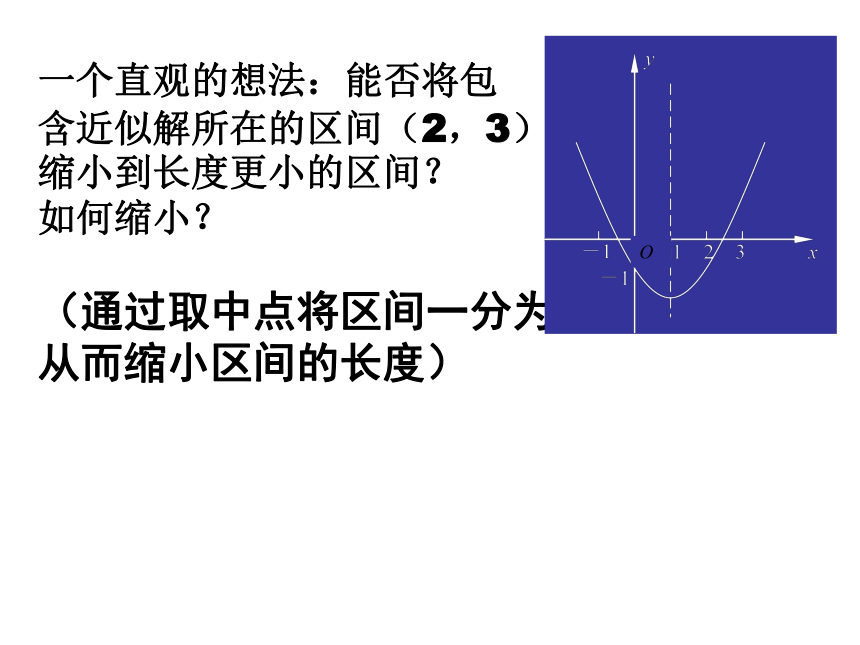
则f(2)· f(3)<0,由二次函数的性质表明图象在区间(2,3)上穿过x轴一次,即方程在区间(2,3)内有惟一解.一个直观的想法:能否将包含近似解所在的区间(2,3)缩小到长度更小的区间?
如何缩小?(通过取中点将区间一分为二,从而缩小区间的长度)2-123(2,3)(2,2.5)(2.25,2.5)(2.375,2.5)(2.375,2.4375)(2.40625,2.4375)(2.40625,2.421875)2.52.252.3752.43752.406252.4218752.4140625-0.000430.021729-0.022460.066406-0.10938-0.43750.25求方程x2-2x-1=0近似解的步骤:(1)确定根所在的大致区间;(2)取该区间的中点x,计算f(x)的值;(4)判断是否达到精确度的要求,确定近似解.(3)根据函数值的符号,确定长度更小的区间,依次进行; 即对于在区间(a,b)上连续不断、且f(a)· f(b)<0的函数y=f(x),通过不断的把方程的解所在的区间一分为二,使区间的两个端点逐步逼近近似解,进而得到近似解的方法叫二分法.定义:二分法
像上述这种求方程近似解的方法称为二分法,它是求一元方程近似解的常用方法.运用二分法的前提是要先判断某个根所在的区间.两点说明:例2 借助计算器,
用二分法求方程lgx=3-x的近似解
(精确到0.1).解:分别画出函数y=lgx
和y=3-x的图象,因此,这个点的横坐标就是方程lgx=3-x的解.由函数y=lgx和y=3-x
的图象可以发现,方程lgx=3-x有惟一解,记为x1,并且这个解在区间(2,3)内. 在
两个函数的图象的交
点处,它们的函数值
相等. 说明这个函数在区间(2,3)内有近似解x1.令f(x)=lgx+x-3,用计算器或计算机算出函数f(x)=lgx+x-3的对应值表:观察上述图表可知:f(2)· f(3)<0, 例2 借助计算器,用二分法求方程lgx=3-x的近似解
(精确到0.1).计算得: f(2.5)=-0.10206<0,所以x1∈(2.5,3);计算得: f(2.75)=0.189333>0,所以x1∈(2.5,2.75);同理:取区间(2.5,2.75)的中点2.625,计算得:
f(2.625)=0.044129>0,所以x1∈(2.5,2.625);
取区间(2.5,2.625)的中点2.5625,计算得:
f(2.5625)=-0.02884<0,所以x1∈(2.5625,2.625).由于|2.5625-2.625|=0.0625<0.1,此时区间(2.5625,2.625)的两个端点精确到0.1的近似值为2.6,所以原方程的近似解为x1≈2.6.例2 借助计算器,用二分法求方程lgx=3-x的近似解
(精确到0.1).[巩固练习]
1. 已知函数f(x)在区间[a,b]上是单调函数,
且 f(a)· f(b)<0,则方程f(x)=0在区间
[a,b]上 ( )
A.至少有一实数根
B.至多有一实数根
C.没有实数根
D.有且仅有唯一的实数根D2. 已知函数f(x)是区间[a,b]上的连续函数,
且f(a)· f(b)<0,则方程f(x)=0在区间
[a,b]上 ( )
A.至少有一实数根
B.至多有一实数根
C.没有实数根
D.有且仅有惟一的实数根A3.(课本P79)试判断方程x3+3x-1=0在区间(0,1)
内是否有解?4.借助计算器用二分法求方程2x+3x-7=0的近似解
(精确到0.1).[课堂小结]
本节课主要介绍了用二分法求方程的近似解,要注意二分法实施的步骤,对具体的方程,往往是要先判断零点所在的区间,然后依次对所在区间减半,最后根据题目所要求的精确度判定并求出的根的近似值(近似解).
方程f(x)=0的实数根之间的关系.(1)通过不断的缩小区间的长度,最后逼近实际的数值.练习:根据上述游戏的思想去计算出无理数 的一个近似值(精确到0.1).课题
用二分法求方程的近似解例1 利用计算器,二分法求方程
x2-2x-1=0的一个近似解.
(计算结果精确到0.1)分析:首先画出函数f(x)=x2-2x-1的图象,从图象上可以发现,方程
x2-2x-1=0的一个根x1
在区间(-1,0)内,另一个根x2在区间(2,3)内.据函数图象,我们发现
f(2)=-1<0,
f(3)=2>0,
则f(2)· f(3)<0,由二次函数的性质表明图象在区间(2,3)上穿过x轴一次,即方程在区间(2,3)内有惟一解.一个直观的想法:能否将包含近似解所在的区间(2,3)缩小到长度更小的区间?
如何缩小?(通过取中点将区间一分为二,从而缩小区间的长度)2-123(2,3)(2,2.5)(2.25,2.5)(2.375,2.5)(2.375,2.4375)(2.40625,2.4375)(2.40625,2.421875)2.52.252.3752.43752.406252.4218752.4140625-0.000430.021729-0.022460.066406-0.10938-0.43750.25求方程x2-2x-1=0近似解的步骤:(1)确定根所在的大致区间;(2)取该区间的中点x,计算f(x)的值;(4)判断是否达到精确度的要求,确定近似解.(3)根据函数值的符号,确定长度更小的区间,依次进行; 即对于在区间(a,b)上连续不断、且f(a)· f(b)<0的函数y=f(x),通过不断的把方程的解所在的区间一分为二,使区间的两个端点逐步逼近近似解,进而得到近似解的方法叫二分法.定义:二分法
像上述这种求方程近似解的方法称为二分法,它是求一元方程近似解的常用方法.运用二分法的前提是要先判断某个根所在的区间.两点说明:例2 借助计算器,
用二分法求方程lgx=3-x的近似解
(精确到0.1).解:分别画出函数y=lgx
和y=3-x的图象,因此,这个点的横坐标就是方程lgx=3-x的解.由函数y=lgx和y=3-x
的图象可以发现,方程lgx=3-x有惟一解,记为x1,并且这个解在区间(2,3)内. 在
两个函数的图象的交
点处,它们的函数值
相等. 说明这个函数在区间(2,3)内有近似解x1.令f(x)=lgx+x-3,用计算器或计算机算出函数f(x)=lgx+x-3的对应值表:观察上述图表可知:f(2)· f(3)<0, 例2 借助计算器,用二分法求方程lgx=3-x的近似解
(精确到0.1).计算得: f(2.5)=-0.10206<0,所以x1∈(2.5,3);计算得: f(2.75)=0.189333>0,所以x1∈(2.5,2.75);同理:取区间(2.5,2.75)的中点2.625,计算得:
f(2.625)=0.044129>0,所以x1∈(2.5,2.625);
取区间(2.5,2.625)的中点2.5625,计算得:
f(2.5625)=-0.02884<0,所以x1∈(2.5625,2.625).由于|2.5625-2.625|=0.0625<0.1,此时区间(2.5625,2.625)的两个端点精确到0.1的近似值为2.6,所以原方程的近似解为x1≈2.6.例2 借助计算器,用二分法求方程lgx=3-x的近似解
(精确到0.1).[巩固练习]
1. 已知函数f(x)在区间[a,b]上是单调函数,
且 f(a)· f(b)<0,则方程f(x)=0在区间
[a,b]上 ( )
A.至少有一实数根
B.至多有一实数根
C.没有实数根
D.有且仅有唯一的实数根D2. 已知函数f(x)是区间[a,b]上的连续函数,
且f(a)· f(b)<0,则方程f(x)=0在区间
[a,b]上 ( )
A.至少有一实数根
B.至多有一实数根
C.没有实数根
D.有且仅有惟一的实数根A3.(课本P79)试判断方程x3+3x-1=0在区间(0,1)
内是否有解?4.借助计算器用二分法求方程2x+3x-7=0的近似解
(精确到0.1).[课堂小结]
本节课主要介绍了用二分法求方程的近似解,要注意二分法实施的步骤,对具体的方程,往往是要先判断零点所在的区间,然后依次对所在区间减半,最后根据题目所要求的精确度判定并求出的根的近似值(近似解).
