17.4 欧姆定律在串、并联电路的应用课件 2022-2023学年人教版九年级全一册物理(共22张PPT)
文档属性
| 名称 | 17.4 欧姆定律在串、并联电路的应用课件 2022-2023学年人教版九年级全一册物理(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-08-01 11:35:43 | ||
图片预览


文档简介
(共22张PPT)
17.4 欧姆定律在串、并联电路的应用
第十七章 欧姆定律
义务教育教科书物理 九年级 全一册
目 录
01
知识梳理
Content
02
课堂讲解
03
课堂小结
04
拓展延伸
一、知识梳理
17.4 欧姆定律在串、并联电路的应用
导体中的电流,跟导体两端的电压成正比,跟导体的电阻成反比。
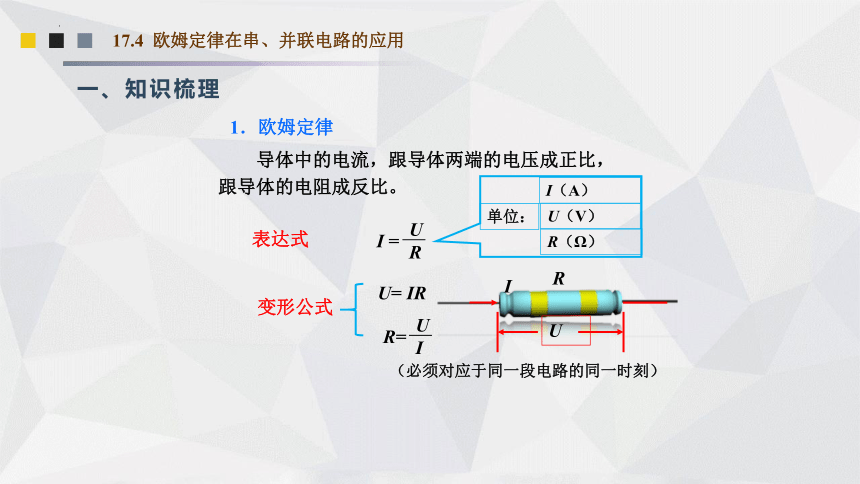
1.欧姆定律
表达式
I =
U
R
R=
U
I
U= IR
R
U
I
(必须对应于同一段电路的同一时刻)
变形公式
R(Ω)
单位:
I(A)
U(V)
一、知识梳理
17.4 欧姆定律在串、并联电路的应用
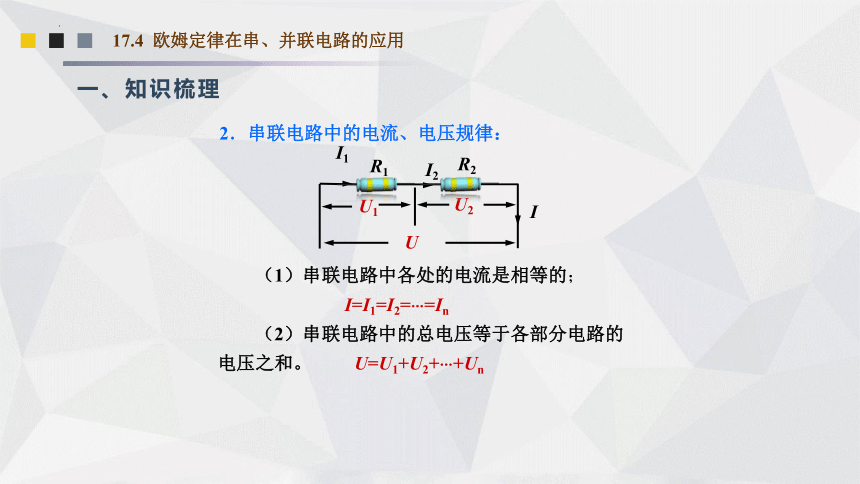
(1)串联电路中各处的电流是相等的;
I=I1=I2=…=In
(2)串联电路中的总电压等于各部分电路的电压之和。 U=U1+U2+…+Un
2.串联电路中的电流、电压规律:
R2
U
I
R1
U1
U2
I2
I1
一、知识梳理
17.4 欧姆定律在串、并联电路的应用
I1
I
I2
R2
R1
U
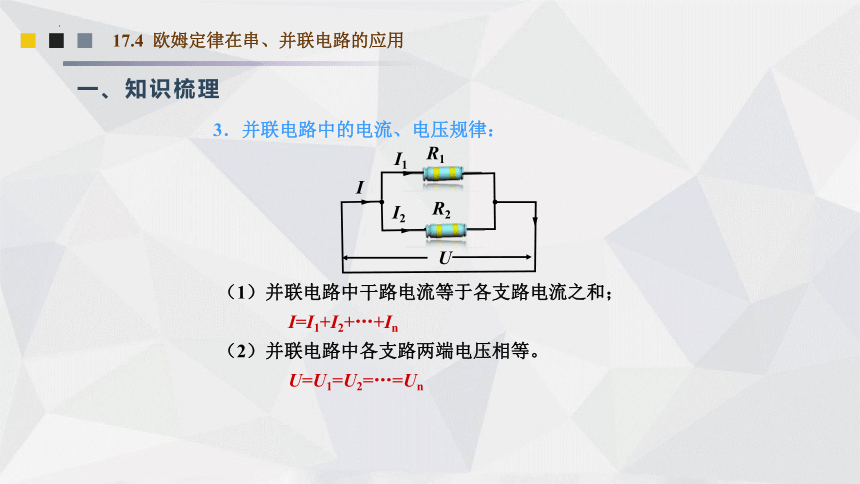
(1)并联电路中干路电流等于各支路电流之和;
I=I1+I2+…+In
(2)并联电路中各支路两端电压相等。
U=U1=U2=…=Un
3.并联电路中的电流、电压规律:
17.4 欧姆定律在串、并联电路的应用
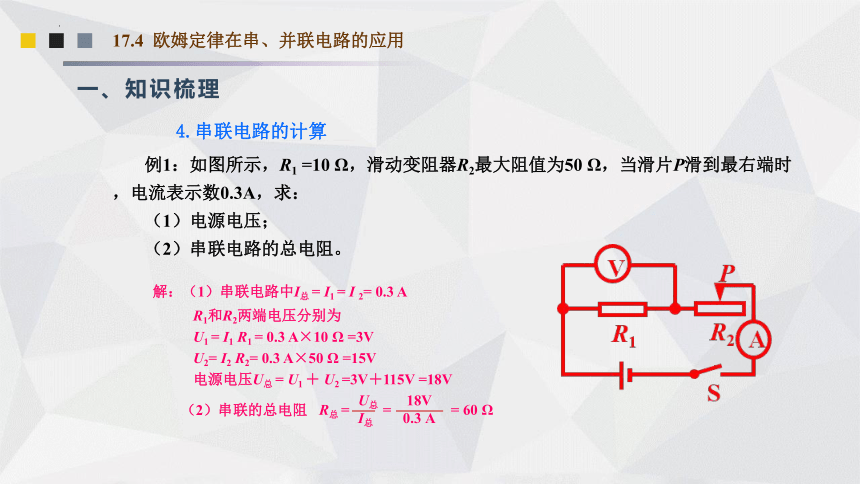
例1:如图所示,R1 =10 Ω,滑动变阻器R2最大阻值为50 Ω,当滑片P滑到最右端时,电流表示数0.3A,求:
(1)电源电压;
(2)串联电路的总电阻。
R1和R2两端电压分别为
U1 = I1 R1 = 0.3 A×10 Ω =3V
U2= I2 R2= 0.3 A×50 Ω =15V
电源电压U总 = U1 + U2 =3V+115V =18V
R总 = = = 60 Ω
U总
I总
18V
0.3 A
(2)串联的总电阻
解:(1)串联电路中I总 = I1 = I 2= 0.3 A
4.串联电路的计算
一、知识梳理
17.4 欧姆定律在串、并联电路的应用
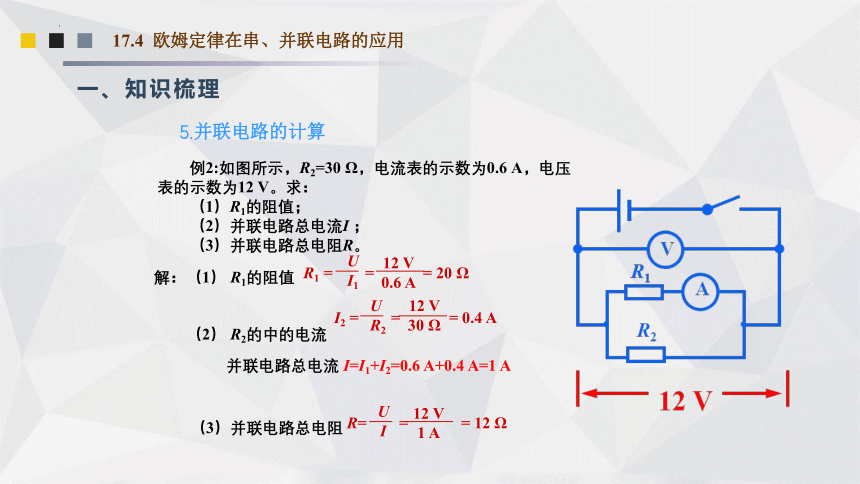
例2:如图所示,R2=30 Ω,电流表的示数为0.6 A,电压表的示数为12 V。求:
(1)R1的阻值;
(2)并联电路总电流I ;
(3)并联电路总电阻R。
解:(1) R1的阻值
(2) R2的中的电流
并联电路总电流 I=I1+I2=0.6 A+0.4 A=1 A
(3)并联电路总电阻
R1 = = = 20 Ω
U
I1
12 V
0.6 A
I2 = = = 0.4 A
U
R2
12 V
30 Ω
R= = = 12 Ω
U
I
12 V
1 A
5.并联电路的计算
一、知识梳理
17.4 欧姆定律在串、并联电路的应用
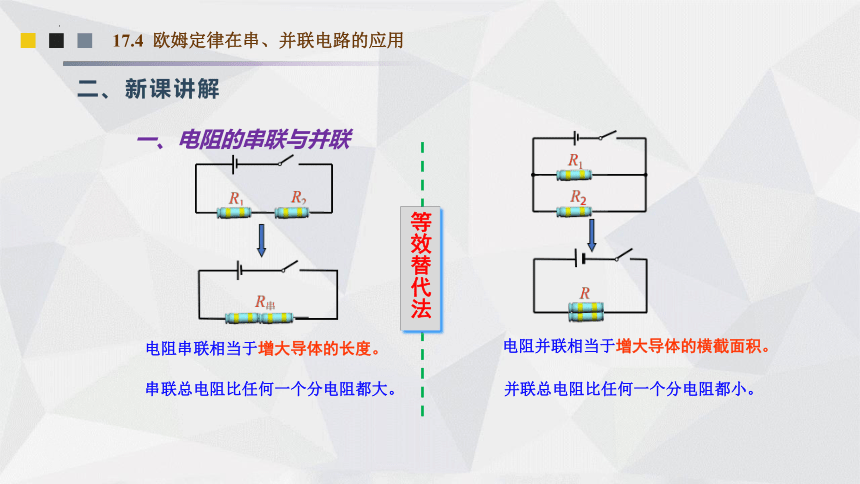
电阻串联相当于增大导体的长度。
串联总电阻比任何一个分电阻都大。
电阻并联相当于增大导体的横截面积。
并联总电阻比任何一个分电阻都小。
等效替代法
一、电阻的串联与并联
二、新课讲解
17.4 欧姆定律在串、并联电路的应用
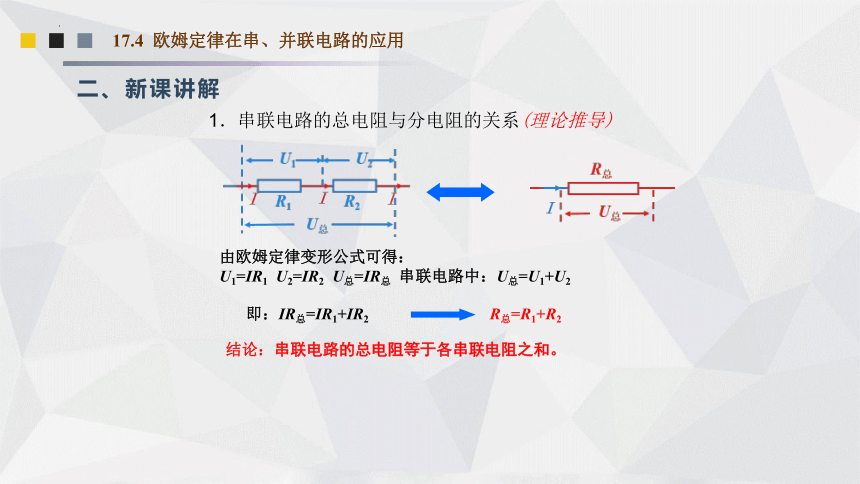
1.串联电路的总电阻与分电阻的关系(理论推导)
由欧姆定律变形公式可得:
U1=IR1 U2=IR2 U总=IR总 串联电路中:U总=U1+U2
即:IR总=IR1+IR2 R总=R1+R2
结论:串联电路的总电阻等于各串联电阻之和。
二、新课讲解
17.4 欧姆定律在串、并联电路的应用
由欧姆定律可得:
并联电路中:I总=I1+I2
结论:并联电路总电阻的倒数等于各个并联电阻的倒数之和。
2.并联电路的总电阻与分电阻的关系(理论推导)
R1
U
I1=
R2
U
I2=
R总
U
I总=
R总
U
R1
U
=
R2
U
+
R总
1
R1
1
=
R2
1
+
二、新课讲解
17.4 欧姆定律在串、并联电路的应用
1.串联电路的总电阻等于各串联电阻之和。
R串= R1+ R2
2.并联电路的总电阻的倒数等于各并联电阻倒数之和。
n个阻值相同的电阻R0串联,总电阻
n个阻值相同的电阻 R0并联,总电阻
R串=nR0
R并
R1
R2
1
1
1
=
+
R1R2
R并=
R1+R2
R0
R并=
n
总结
二、新课讲解
17.4 欧姆定律在串、并联电路的应用
例1:如图所示,电阻R1为12Ω,电源两端电压为6V。开关闭合后,求:
(1)当滑动变阻器R2接入电路的电阻为48Ω时,通过电阻R1的电流I ;
(2)当滑动变阻器R2接入电路的电阻为8Ω时,通过电阻R1的电流I′。
解:由图可知,R1与R2串联。
(1)串联的总电阻是R=R1+R2=12Ω+48Ω=60Ω
I= = = 0.1 A
U
R
6 V
60 Ω
通过R1的电流为
(2)串联的总电阻是R ′ =R1+R2 ′ =12Ω+8Ω=20Ω
通过R1的电流为
I ′ = = = 0.3 A
U
R ′
6 V
20 Ω
二、串并联电路的计算
二、新课讲解
17.4 欧姆定律在串、并联电路的应用
例2: 如图所示,已知I=0.9 A,I2=0.3 A,电源电压为36 V,那么灯L1的电阻R1多大?灯L2的电阻R2以及并联的总电阻多大?
解: ∵ 灯L1和灯L2并联
∴ I = I1 + I2
I1 = I - I2 = 0.9 A -0.3 A = 0.6 A
而 U1 = U2 =U= 36 V
R1= = = 60 Ω
U1
I1
36 V
0.6 A
R2= = = 120 Ω
U2
I2
36 V
0.3 A
R总= = = 40Ω
U
I
36 V
0.9A
二、新课讲解
17.4 欧姆定律在串、并联电路的应用
R1一定
例3.变阻器的滑片P向右移动过程中,三个电表的示数如何变化?
分析:
____;
示数变大
V2
V1
A
示数变小
____;
____。
R2 ↑→ R ↑→I↓= I1 ↓ = I2
U1 ↓
U2 ↑
U不变
示数变小
三、动态电路分析
二、新课讲解
三、课堂小结
17.4 欧姆定律在串、并联电路的应用
求解电路计算题的步骤
(1)根据题意分析各电路状态下电阻之间的连接方式,画出等效电路图。
(2)通过审题,明确题目给出的已知条件和未知量,并将已知量的符号、数值和单位,未知量的符号,在电路图上标明。
(3)每一步求解过程必须包括三步:
写公式——代入数值和单位——得出结果。
四、拓展延伸
17.4 欧姆定律在串、并联电路的应用
1.一个小灯泡阻值为12Ω,正常工作时的电流为0.3 A,现要将其接入12 V 的电路中,要求仍能正常发光,则应_______联一个阻值为________Ω的电阻。
串
28
四、拓展延伸
17.4 欧姆定律在串、并联电路的应用
2.甲乙两电阻之比为3:1,将它们串联在电路中时,它们两端的电压之比为( )
A.1:2 B.3:1
C.1:1 D.无法比较
B
17.4 欧姆定律在串、并联电路的应用
3.下列几组电阻并联后,等效阻值最小的一组是( )
A.30Ω和25Ω B.20Ω和35Ω
C.10Ω和45Ω D.5Ω和50Ω
D
四、拓展延伸
17.4 欧姆定律在串、并联电路的应用
4.如图所示,AB和BC是由同种材料制成的长度相同、横截面积不同的两段导体,将它们串联后连入电路中.比较这两段导体两端的电压及通过它们的电流的大小,有( )
A.UAB>UBC IAB<IBC B.UAB<UBC IAB = IBC
C. UAB>UBC IAB=IBC D.UAB=UBC IAB<IBC
C
四、拓展延伸
A
B
C
17.4 欧姆定律在串、并联电路的应用
5.串联电路中有两个电阻,阻值分别为5 和10 ,将它们接在6V的电源上,那么流过它们的电流会是多大?
流过两个电阻的电流都是0.4A。
解:
四、拓展延伸
17.4 欧姆定律在串、并联电路的应用
6.两个电阻串联在一个电路中,电路两端的电压是27V,两个电阻的阻值分别是3 和6 ,请计算出每个电阻两端的电压。
解:
四、拓展延伸
四、知识拓展
7.小明家的电话不能使用,经过电信公司机房人员初步测试,判断为接入小明家的电话线某处短路,为了确定短路的具体位置,机房人员利用测量仪器接成如图所示的电路进行测量。已知电话线由两根导线并排而成,该用户家到机房的电话线长10 km,设单根电话线每米的电阻为2×l0-3Ω ,测量时电压表示数为16V,电流表示数为1A。若只考虑电话线的电阻,求:
(1)该用户家到机房单根电话线的电阻值;
(2)短路位置到机房的距离S。
17.4 欧姆定律在串、并联电路的应用
解:(1)该用户家到机房的单根电话线的电阻值
是10000×3×10-3Ω=30 Ω ;
(2)短路位置到机房电话线的总电阻R总=U/I=16V/1A=16 Ω ,短路位置到机房单根电话线的电阻R′=×16 Ω =8 Ω ,短路位置到机房的距离S= =4000m=4km
17.4 欧姆定律在串、并联电路的应用
第十七章 欧姆定律
义务教育教科书物理 九年级 全一册
目 录
01
知识梳理
Content
02
课堂讲解
03
课堂小结
04
拓展延伸
一、知识梳理
17.4 欧姆定律在串、并联电路的应用
导体中的电流,跟导体两端的电压成正比,跟导体的电阻成反比。
1.欧姆定律
表达式
I =
U
R
R=
U
I
U= IR
R
U
I
(必须对应于同一段电路的同一时刻)
变形公式
R(Ω)
单位:
I(A)
U(V)
一、知识梳理
17.4 欧姆定律在串、并联电路的应用
(1)串联电路中各处的电流是相等的;
I=I1=I2=…=In
(2)串联电路中的总电压等于各部分电路的电压之和。 U=U1+U2+…+Un
2.串联电路中的电流、电压规律:
R2
U
I
R1
U1
U2
I2
I1
一、知识梳理
17.4 欧姆定律在串、并联电路的应用
I1
I
I2
R2
R1
U
(1)并联电路中干路电流等于各支路电流之和;
I=I1+I2+…+In
(2)并联电路中各支路两端电压相等。
U=U1=U2=…=Un
3.并联电路中的电流、电压规律:
17.4 欧姆定律在串、并联电路的应用
例1:如图所示,R1 =10 Ω,滑动变阻器R2最大阻值为50 Ω,当滑片P滑到最右端时,电流表示数0.3A,求:
(1)电源电压;
(2)串联电路的总电阻。
R1和R2两端电压分别为
U1 = I1 R1 = 0.3 A×10 Ω =3V
U2= I2 R2= 0.3 A×50 Ω =15V
电源电压U总 = U1 + U2 =3V+115V =18V
R总 = = = 60 Ω
U总
I总
18V
0.3 A
(2)串联的总电阻
解:(1)串联电路中I总 = I1 = I 2= 0.3 A
4.串联电路的计算
一、知识梳理
17.4 欧姆定律在串、并联电路的应用
例2:如图所示,R2=30 Ω,电流表的示数为0.6 A,电压表的示数为12 V。求:
(1)R1的阻值;
(2)并联电路总电流I ;
(3)并联电路总电阻R。
解:(1) R1的阻值
(2) R2的中的电流
并联电路总电流 I=I1+I2=0.6 A+0.4 A=1 A
(3)并联电路总电阻
R1 = = = 20 Ω
U
I1
12 V
0.6 A
I2 = = = 0.4 A
U
R2
12 V
30 Ω
R= = = 12 Ω
U
I
12 V
1 A
5.并联电路的计算
一、知识梳理
17.4 欧姆定律在串、并联电路的应用
电阻串联相当于增大导体的长度。
串联总电阻比任何一个分电阻都大。
电阻并联相当于增大导体的横截面积。
并联总电阻比任何一个分电阻都小。
等效替代法
一、电阻的串联与并联
二、新课讲解
17.4 欧姆定律在串、并联电路的应用
1.串联电路的总电阻与分电阻的关系(理论推导)
由欧姆定律变形公式可得:
U1=IR1 U2=IR2 U总=IR总 串联电路中:U总=U1+U2
即:IR总=IR1+IR2 R总=R1+R2
结论:串联电路的总电阻等于各串联电阻之和。
二、新课讲解
17.4 欧姆定律在串、并联电路的应用
由欧姆定律可得:
并联电路中:I总=I1+I2
结论:并联电路总电阻的倒数等于各个并联电阻的倒数之和。
2.并联电路的总电阻与分电阻的关系(理论推导)
R1
U
I1=
R2
U
I2=
R总
U
I总=
R总
U
R1
U
=
R2
U
+
R总
1
R1
1
=
R2
1
+
二、新课讲解
17.4 欧姆定律在串、并联电路的应用
1.串联电路的总电阻等于各串联电阻之和。
R串= R1+ R2
2.并联电路的总电阻的倒数等于各并联电阻倒数之和。
n个阻值相同的电阻R0串联,总电阻
n个阻值相同的电阻 R0并联,总电阻
R串=nR0
R并
R1
R2
1
1
1
=
+
R1R2
R并=
R1+R2
R0
R并=
n
总结
二、新课讲解
17.4 欧姆定律在串、并联电路的应用
例1:如图所示,电阻R1为12Ω,电源两端电压为6V。开关闭合后,求:
(1)当滑动变阻器R2接入电路的电阻为48Ω时,通过电阻R1的电流I ;
(2)当滑动变阻器R2接入电路的电阻为8Ω时,通过电阻R1的电流I′。
解:由图可知,R1与R2串联。
(1)串联的总电阻是R=R1+R2=12Ω+48Ω=60Ω
I= = = 0.1 A
U
R
6 V
60 Ω
通过R1的电流为
(2)串联的总电阻是R ′ =R1+R2 ′ =12Ω+8Ω=20Ω
通过R1的电流为
I ′ = = = 0.3 A
U
R ′
6 V
20 Ω
二、串并联电路的计算
二、新课讲解
17.4 欧姆定律在串、并联电路的应用
例2: 如图所示,已知I=0.9 A,I2=0.3 A,电源电压为36 V,那么灯L1的电阻R1多大?灯L2的电阻R2以及并联的总电阻多大?
解: ∵ 灯L1和灯L2并联
∴ I = I1 + I2
I1 = I - I2 = 0.9 A -0.3 A = 0.6 A
而 U1 = U2 =U= 36 V
R1= = = 60 Ω
U1
I1
36 V
0.6 A
R2= = = 120 Ω
U2
I2
36 V
0.3 A
R总= = = 40Ω
U
I
36 V
0.9A
二、新课讲解
17.4 欧姆定律在串、并联电路的应用
R1一定
例3.变阻器的滑片P向右移动过程中,三个电表的示数如何变化?
分析:
____;
示数变大
V2
V1
A
示数变小
____;
____。
R2 ↑→ R ↑→I↓= I1 ↓ = I2
U1 ↓
U2 ↑
U不变
示数变小
三、动态电路分析
二、新课讲解
三、课堂小结
17.4 欧姆定律在串、并联电路的应用
求解电路计算题的步骤
(1)根据题意分析各电路状态下电阻之间的连接方式,画出等效电路图。
(2)通过审题,明确题目给出的已知条件和未知量,并将已知量的符号、数值和单位,未知量的符号,在电路图上标明。
(3)每一步求解过程必须包括三步:
写公式——代入数值和单位——得出结果。
四、拓展延伸
17.4 欧姆定律在串、并联电路的应用
1.一个小灯泡阻值为12Ω,正常工作时的电流为0.3 A,现要将其接入12 V 的电路中,要求仍能正常发光,则应_______联一个阻值为________Ω的电阻。
串
28
四、拓展延伸
17.4 欧姆定律在串、并联电路的应用
2.甲乙两电阻之比为3:1,将它们串联在电路中时,它们两端的电压之比为( )
A.1:2 B.3:1
C.1:1 D.无法比较
B
17.4 欧姆定律在串、并联电路的应用
3.下列几组电阻并联后,等效阻值最小的一组是( )
A.30Ω和25Ω B.20Ω和35Ω
C.10Ω和45Ω D.5Ω和50Ω
D
四、拓展延伸
17.4 欧姆定律在串、并联电路的应用
4.如图所示,AB和BC是由同种材料制成的长度相同、横截面积不同的两段导体,将它们串联后连入电路中.比较这两段导体两端的电压及通过它们的电流的大小,有( )
A.UAB>UBC IAB<IBC B.UAB<UBC IAB = IBC
C. UAB>UBC IAB=IBC D.UAB=UBC IAB<IBC
C
四、拓展延伸
A
B
C
17.4 欧姆定律在串、并联电路的应用
5.串联电路中有两个电阻,阻值分别为5 和10 ,将它们接在6V的电源上,那么流过它们的电流会是多大?
流过两个电阻的电流都是0.4A。
解:
四、拓展延伸
17.4 欧姆定律在串、并联电路的应用
6.两个电阻串联在一个电路中,电路两端的电压是27V,两个电阻的阻值分别是3 和6 ,请计算出每个电阻两端的电压。
解:
四、拓展延伸
四、知识拓展
7.小明家的电话不能使用,经过电信公司机房人员初步测试,判断为接入小明家的电话线某处短路,为了确定短路的具体位置,机房人员利用测量仪器接成如图所示的电路进行测量。已知电话线由两根导线并排而成,该用户家到机房的电话线长10 km,设单根电话线每米的电阻为2×l0-3Ω ,测量时电压表示数为16V,电流表示数为1A。若只考虑电话线的电阻,求:
(1)该用户家到机房单根电话线的电阻值;
(2)短路位置到机房的距离S。
17.4 欧姆定律在串、并联电路的应用
解:(1)该用户家到机房的单根电话线的电阻值
是10000×3×10-3Ω=30 Ω ;
(2)短路位置到机房电话线的总电阻R总=U/I=16V/1A=16 Ω ,短路位置到机房单根电话线的电阻R′=×16 Ω =8 Ω ,短路位置到机房的距离S= =4000m=4km
同课章节目录
- 第十三章 内能
- 第1节 分子热运动
- 第2节 内能
- 第3节 比热容
- 第十四章 内能的利用
- 第1节 热机
- 第2节 热机的效率
- 第3节 能量的转化和守恒
- 第十五章 电流和电路
- 第1节 两种电荷
- 第2节 电流和电路
- 第3节 串联和并联
- 第4节 电流的测量
- 第5节 串、并联电路中电流的规律
- 第十六章 电压 电阻
- 第1节 电压
- 第2节 串、并联电路电压的规律
- 第3节 电阻
- 第4节 变阻器
- 第十七章 欧姆定律
- 第1节 电流与电压和电阻的关系
- 第2节 欧姆定律
- 第3节 电阻的测量
- 第4节 欧姆定律在串、并联电路中的应用
- 第十八章 电功率
- 第1节 电能 电功
- 第2节 电功率
- 第3节 测量小灯泡的电功率
- 第4节 焦耳定律
- 第十九章 生活用电
- 第1节 家庭电路
- 第2节 家庭电路电流过大的原因
- 第3节 安全用电
- 第二十章 电与磁
- 第1节 磁现象 磁场
- 第2节 电生磁
- 第3节 电磁铁 电磁继电器
- 第4节 电动机
- 第5节 磁生电
- 第二十一章 信息的传递
- 第1节 现代顺风耳──电话
- 第2节 电磁波的海洋
- 第3节 广播、电视和移动通信
- 第4节 越来越宽的信息之路
- 第二十二章 能源与可持续发展
- 第1节 能源
- 第2节 核能
- 第3节 太阳能
- 第4节 能源与可持续发展
