函数模型及其应用[上学期]
图片预览











文档简介
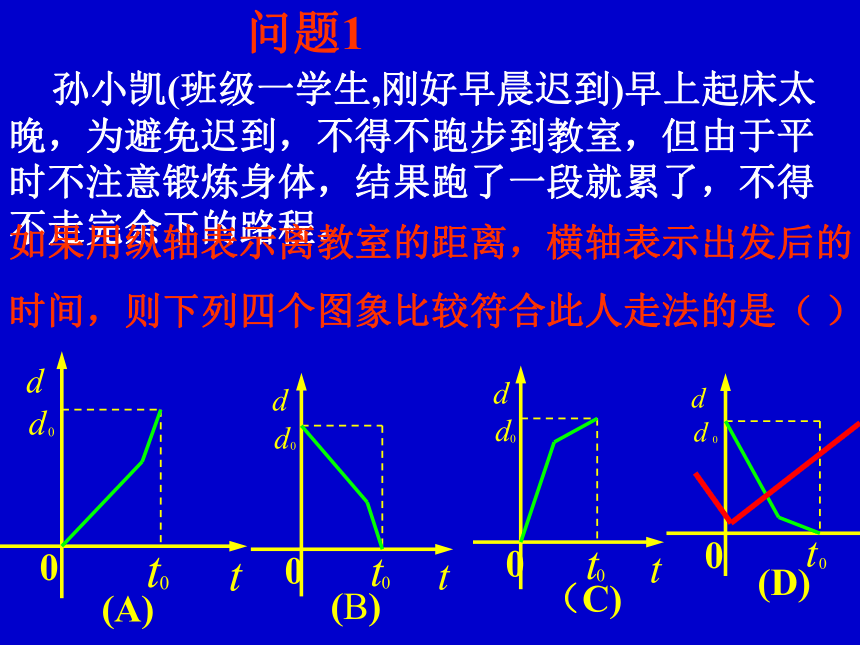
课件43张PPT。函数模型及其应用(1) 孙小凯(班级一学生,刚好早晨迟到)早上起床太晚,为避免迟到,不得不跑步到教室,但由于平时不注意锻炼身体,结果跑了一段就累了,不得不走完余下的路程。问题1如果用纵轴表示离教室的距离,横轴表示出发后的
时间,则下列四个图象比较符合此人走法的是( )
问题2 韦老师今天从县中到二中上课,来的时候坐了
出租车。我们知道洪泽出租车的价格,凡上车起步
价为4元,行程不超过3km者均按此价收费,
行程超过3km,按1.5元/km收费。
县中到二中的路程是 4公里,问韦老师今天坐车
用了多少钱?
县中到二中的路程是 x公里,问韦老师今天坐车
会用多少钱?
实际问题数学模型数学模型的解实际问题的解答 求解数学应用问题的思路和方法,我们可以用
示意图表示为:数学模型例1、某计算机集团公司生产某种型号的计算机的固定成本为200万元,生产每台计算机的可变成本为3000元,每台计算机的售价为5000元,分别写出总成本C(万元),单位成本P(万元)、销售收入R(万元)以及利润L(万元)关于总量x(台)的函数关系式。例2、物体在常温下的温度变化可以用牛顿冷却规律来描述:设物体的初始温度是T0,经过一定时间t后的温度是T,则 ,其中 表示
环境温度,称 h为半衰期。
现有一杯用88℃热水冲的速溶咖啡,放在24℃的房间中,如果咖啡降温到40℃需要20min,那么降到35℃时,需要多长时间(结果精确到0.1)?例3、在经济学中,函数 的边际函
数 定义为 。某公司每月最多生产100台报警系统,生产x台的收入函数为 (单位:元),其成本函数为 (单位:元),利润是收入与成本之差。
(1)求利润函数
及边际利润函数 ;
(2)利润函数 与边际利润函数 是具有相同的最大值?因此,解决应用题的一般程序是:
①审题:弄清题意,分清条件和结论,理顺数量关系;
②建模:将文字语言转化为数学语言,利用数学知识,建立相应的数学模型;
③解模:求解数学模型,得出数学结论;
④还原:将用数学知识和方法得出的结论,还原为实际问题的意义.欢迎谢谢合作作业 p88 3、4
函数模型及其应用(2)解决应用题的一般程序是:
①审题:弄清题意,分清条件和结论,理顺数量关系;
②建模:将文字语言转化为数学语言,利用数学知识,建立相应的数学模型;
③解模:求解数学模型,得出数学结论;
④还原:将用数学知识和方法得出的结论,还原为实际问题的意义.解之得例2.某房地产公司要在荒地ABCDE(如图)上划出一块长方形的地面修建一幢公寓楼,已知EF=80m,BC=70m,BF=30m,
AF=20m,问:
如何设计才能使公
寓楼地面面积最大?
最大面积是多少?D例1:如图,有一块半径为R的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上。问:腰为多少时,梯形周长最大?解:设腰长AD=BC=x,周长为yE练习1.有一批材料可以建成200m的围墙,如果用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如下图所示),则围成的矩形最大面积为 ________m2(围墙厚度不计).解析:设矩形宽为xm,
则矩形长为(200-4x)m,
则矩形面积为
S=x(200-4x)
=-4(x-25)2+2500
(0<x<50),
∴x=25时,S有最大值2500m2. 2.有甲、乙两种产品,生产这两种产品所获得利润分别为p和q(万元),它们与投入的资金x(万元)的关系分别为 , 。
今投入3万元资金生产甲、乙两种产品,为了获得最大利润,对甲乙两种产品的投入分别应为多少万元?此时最大利润是多少万元?3某产品的成本y(万元)与产量x(台)之间的函数关系
,若每台产品的售价为25万元,则生产者不“亏本”(即销售收入不小于总成本)的最低产量台数为小结:2.解题过程:从问题出发,引进数学符号,建立函数关系式,再研究函数关系式的定义域,并结合问题的实际意义做出回答.
即建立数学模型,并推理演算求出数学模型的解,再结合实际做出回答.1.解题四步骤:设、列、解、答.欢迎谢谢合作函数模型及其应用(3)例1、某旅社有客房300间,每间日房租为20元,每天都客满,公司欲提高档次,并提高租金,如果每间客房每日增加2元,客房出租数就会减少10间,若不考虑其它因素,旅社将房间租金提高多少时,每天客房租金总收入最高? 点拨:由题设可知,每天客房总的租金是增加2元的倍数的函数。设提高为x个2元,则依题意可算出总租金(用y表 示)的表达式,由于房间数不太多,为了帮助同学理解这道应用题,我们先用列表法求解,然后再用函数的解析表达式求解。解:设客房租金每间提高x个2元,Y=(20+2x)(300-10x)=-20x2+600x-200x+6000=-20(x2-20x+100-100)+6000=-20(x-10)2+8000则将有10x间客房空出,客房租金的总收入为由此得到,当x=10时,y的最大值为8000,即每间租金为20+10×2=40(元)时客房租金总收入最高,每天为8000元。总结: 通过列表的形式求解,直观性强,有助于同学理解,但运算过程比较繁琐,作为探求思路的方法还是可行的;
根据题目的条件列出函数关系式,利用二次函数求极值,是常用的方法。练习:1、将进货单价为80元的商品按90元一个出售时,能卖出400个,根据经验,该商品每个上涨1元,其销售量就减少20个,为获得最大利润,售价应定为多少元?最大利润是多少?2、某车间最大生产能力为月生产100台机床,至少要完成40台才能保本,当生产x台时的总成本函数为G(x)=x2+10x(百元),按市场规律,价格为P=970-5x(x需求量)可以销售完,试写出利润函数,并求出生产多少台时,利润最大。3、某商场出售一种商品,(原来)每天可卖出1000件,每件可获利4元。根据经验,若单件商品的价格每减少0.1元,每天的销售量就会多出100件。从获得最好的经济效益的角度来看,该商品的单价应比现在减少_____元函数模型及其应用(4)例题、一家报刊摊点,从报社买进报纸价格是每份0.24元,卖出是每份0.40元,卖不掉的报纸还可以每份0.08元的价格退回报社,在一个月的30天里,有20天每天可卖出300份,其余10天,每天卖出200份,但这30天里,每天从报社买进的份数必须相同,这家报刊摊点应该每天从报社进多少份报纸,才能获得最大利润,一个月可赚多少钱. (2)当200 y=(0.4-0.24) ·10·200-(0.24-0.08)·10·(x-200)+
(0.4-0.24)·20·x=640+1.6x
≤640+1.6·300=1120解:设这家报刊摊点每天从报社买进x份报纸,一个月可赚y元。
(1)当x≤200时,
y=(0.4-0.24) ·30 ·x·=4.8x≤4.8·200=969.
(3)当x>300时,
y=(0.4-0.24) ·10·200-(0.24-0.08)·10·(x-200)
+(0.4-0.24)·20·300-(0.24-0.08)(x-300)·20
=2560-4.8x<2560-4.8·300=1120总结:求分段函数的最值,应先求出函数在各部分的最值,然后取各部分的最值的最大值为整个函数的最大值,取各部分的最小者为整个函数的最小值.变式:如图,一动点P自边长为1的正方形的边界运动一周后再回到A点,若点P的路程为x,点P到顶点A的距离为y,
求A,P两点间的
距离y与点P的
路程x之间的函
数关系式。2、某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:
其中x是仪器的月产量。
(1)将利润表示为当月产最的函数
(2)求每月生产多少台仪器时,公司所获利润最大?最大利润为多少元?例2.在一定范围内,某种产品的购买量为y t,与单价x元之间满足一次函数关系。
如果购买1000t,每吨为800元,如果购买2000t,每吨为700元,一客户购买400t,单价应该为
( )
A.820 元 B.840元 C.860元 D.880元c解:设在进价基础上增加x元后,日均经营利润为y元,则有日均销售量为 `②利润怎样产生的?销售单价每增加1元,日均销售量就减少40桶 1、 某车站有快、慢两种车,始发站距终点站7.2km,
慢车到终点站需16min,快车比慢车晚发车3min,
且行驶10min到达终点站。
试写出两车所行路程关于慢车行驶时间的函数关系式。
并回答:两车何时相遇?相遇时距始发站多远?巩固练习3、用一条长为L米的钢丝折成一个矩形,该矩形长为多少时,面积最大?巩固练习
时间,则下列四个图象比较符合此人走法的是( )
问题2 韦老师今天从县中到二中上课,来的时候坐了
出租车。我们知道洪泽出租车的价格,凡上车起步
价为4元,行程不超过3km者均按此价收费,
行程超过3km,按1.5元/km收费。
县中到二中的路程是 4公里,问韦老师今天坐车
用了多少钱?
县中到二中的路程是 x公里,问韦老师今天坐车
会用多少钱?
实际问题数学模型数学模型的解实际问题的解答 求解数学应用问题的思路和方法,我们可以用
示意图表示为:数学模型例1、某计算机集团公司生产某种型号的计算机的固定成本为200万元,生产每台计算机的可变成本为3000元,每台计算机的售价为5000元,分别写出总成本C(万元),单位成本P(万元)、销售收入R(万元)以及利润L(万元)关于总量x(台)的函数关系式。例2、物体在常温下的温度变化可以用牛顿冷却规律来描述:设物体的初始温度是T0,经过一定时间t后的温度是T,则 ,其中 表示
环境温度,称 h为半衰期。
现有一杯用88℃热水冲的速溶咖啡,放在24℃的房间中,如果咖啡降温到40℃需要20min,那么降到35℃时,需要多长时间(结果精确到0.1)?例3、在经济学中,函数 的边际函
数 定义为 。某公司每月最多生产100台报警系统,生产x台的收入函数为 (单位:元),其成本函数为 (单位:元),利润是收入与成本之差。
(1)求利润函数
及边际利润函数 ;
(2)利润函数 与边际利润函数 是具有相同的最大值?因此,解决应用题的一般程序是:
①审题:弄清题意,分清条件和结论,理顺数量关系;
②建模:将文字语言转化为数学语言,利用数学知识,建立相应的数学模型;
③解模:求解数学模型,得出数学结论;
④还原:将用数学知识和方法得出的结论,还原为实际问题的意义.欢迎谢谢合作作业 p88 3、4
函数模型及其应用(2)解决应用题的一般程序是:
①审题:弄清题意,分清条件和结论,理顺数量关系;
②建模:将文字语言转化为数学语言,利用数学知识,建立相应的数学模型;
③解模:求解数学模型,得出数学结论;
④还原:将用数学知识和方法得出的结论,还原为实际问题的意义.解之得例2.某房地产公司要在荒地ABCDE(如图)上划出一块长方形的地面修建一幢公寓楼,已知EF=80m,BC=70m,BF=30m,
AF=20m,问:
如何设计才能使公
寓楼地面面积最大?
最大面积是多少?D例1:如图,有一块半径为R的半圆形钢板,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上。问:腰为多少时,梯形周长最大?解:设腰长AD=BC=x,周长为yE练习1.有一批材料可以建成200m的围墙,如果用此材料在一边靠墙的地方围成一块矩形场地,中间用同样的材料隔成三个面积相等的矩形(如下图所示),则围成的矩形最大面积为 ________m2(围墙厚度不计).解析:设矩形宽为xm,
则矩形长为(200-4x)m,
则矩形面积为
S=x(200-4x)
=-4(x-25)2+2500
(0<x<50),
∴x=25时,S有最大值2500m2. 2.有甲、乙两种产品,生产这两种产品所获得利润分别为p和q(万元),它们与投入的资金x(万元)的关系分别为 , 。
今投入3万元资金生产甲、乙两种产品,为了获得最大利润,对甲乙两种产品的投入分别应为多少万元?此时最大利润是多少万元?3某产品的成本y(万元)与产量x(台)之间的函数关系
,若每台产品的售价为25万元,则生产者不“亏本”(即销售收入不小于总成本)的最低产量台数为小结:2.解题过程:从问题出发,引进数学符号,建立函数关系式,再研究函数关系式的定义域,并结合问题的实际意义做出回答.
即建立数学模型,并推理演算求出数学模型的解,再结合实际做出回答.1.解题四步骤:设、列、解、答.欢迎谢谢合作函数模型及其应用(3)例1、某旅社有客房300间,每间日房租为20元,每天都客满,公司欲提高档次,并提高租金,如果每间客房每日增加2元,客房出租数就会减少10间,若不考虑其它因素,旅社将房间租金提高多少时,每天客房租金总收入最高? 点拨:由题设可知,每天客房总的租金是增加2元的倍数的函数。设提高为x个2元,则依题意可算出总租金(用y表 示)的表达式,由于房间数不太多,为了帮助同学理解这道应用题,我们先用列表法求解,然后再用函数的解析表达式求解。解:设客房租金每间提高x个2元,Y=(20+2x)(300-10x)=-20x2+600x-200x+6000=-20(x2-20x+100-100)+6000=-20(x-10)2+8000则将有10x间客房空出,客房租金的总收入为由此得到,当x=10时,y的最大值为8000,即每间租金为20+10×2=40(元)时客房租金总收入最高,每天为8000元。总结: 通过列表的形式求解,直观性强,有助于同学理解,但运算过程比较繁琐,作为探求思路的方法还是可行的;
根据题目的条件列出函数关系式,利用二次函数求极值,是常用的方法。练习:1、将进货单价为80元的商品按90元一个出售时,能卖出400个,根据经验,该商品每个上涨1元,其销售量就减少20个,为获得最大利润,售价应定为多少元?最大利润是多少?2、某车间最大生产能力为月生产100台机床,至少要完成40台才能保本,当生产x台时的总成本函数为G(x)=x2+10x(百元),按市场规律,价格为P=970-5x(x需求量)可以销售完,试写出利润函数,并求出生产多少台时,利润最大。3、某商场出售一种商品,(原来)每天可卖出1000件,每件可获利4元。根据经验,若单件商品的价格每减少0.1元,每天的销售量就会多出100件。从获得最好的经济效益的角度来看,该商品的单价应比现在减少_____元函数模型及其应用(4)例题、一家报刊摊点,从报社买进报纸价格是每份0.24元,卖出是每份0.40元,卖不掉的报纸还可以每份0.08元的价格退回报社,在一个月的30天里,有20天每天可卖出300份,其余10天,每天卖出200份,但这30天里,每天从报社买进的份数必须相同,这家报刊摊点应该每天从报社进多少份报纸,才能获得最大利润,一个月可赚多少钱. (2)当200
(0.4-0.24)·20·x=640+1.6x
≤640+1.6·300=1120解:设这家报刊摊点每天从报社买进x份报纸,一个月可赚y元。
(1)当x≤200时,
y=(0.4-0.24) ·30 ·x·=4.8x≤4.8·200=969.
(3)当x>300时,
y=(0.4-0.24) ·10·200-(0.24-0.08)·10·(x-200)
+(0.4-0.24)·20·300-(0.24-0.08)(x-300)·20
=2560-4.8x<2560-4.8·300=1120总结:求分段函数的最值,应先求出函数在各部分的最值,然后取各部分的最值的最大值为整个函数的最大值,取各部分的最小者为整个函数的最小值.变式:如图,一动点P自边长为1的正方形的边界运动一周后再回到A点,若点P的路程为x,点P到顶点A的距离为y,
求A,P两点间的
距离y与点P的
路程x之间的函
数关系式。2、某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元,已知总收益满足函数:
其中x是仪器的月产量。
(1)将利润表示为当月产最的函数
(2)求每月生产多少台仪器时,公司所获利润最大?最大利润为多少元?例2.在一定范围内,某种产品的购买量为y t,与单价x元之间满足一次函数关系。
如果购买1000t,每吨为800元,如果购买2000t,每吨为700元,一客户购买400t,单价应该为
( )
A.820 元 B.840元 C.860元 D.880元c解:设在进价基础上增加x元后,日均经营利润为y元,则有日均销售量为 `②利润怎样产生的?销售单价每增加1元,日均销售量就减少40桶 1、 某车站有快、慢两种车,始发站距终点站7.2km,
慢车到终点站需16min,快车比慢车晚发车3min,
且行驶10min到达终点站。
试写出两车所行路程关于慢车行驶时间的函数关系式。
并回答:两车何时相遇?相遇时距始发站多远?巩固练习3、用一条长为L米的钢丝折成一个矩形,该矩形长为多少时,面积最大?巩固练习
