第23章 解直角三角形单元测试卷(较易)(含答案)
文档属性
| 名称 | 第23章 解直角三角形单元测试卷(较易)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 255.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 19:01:17 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
沪科版初中数学九年级上册第23章《解直角三角形》单元测试卷
考试范围:第23章;考试时间:120分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36分)
在中,,,,则的值是( )
A. B. C. D.
在中,,,则( )
A. B. C. D.
如图,在中,,设,,所对的边分别为,,,则( )
A.
B.
C.
D.
下列各式中,运算结果是分数的是( )
A. B. C. D.
如图,在的正方形网格中,每个小正方形的边长都是,的顶点都在这些小正方形的顶点上,那么的值为( )
A.
B.
C.
D.
在中,,,,则长是( )
A. B. C. D.
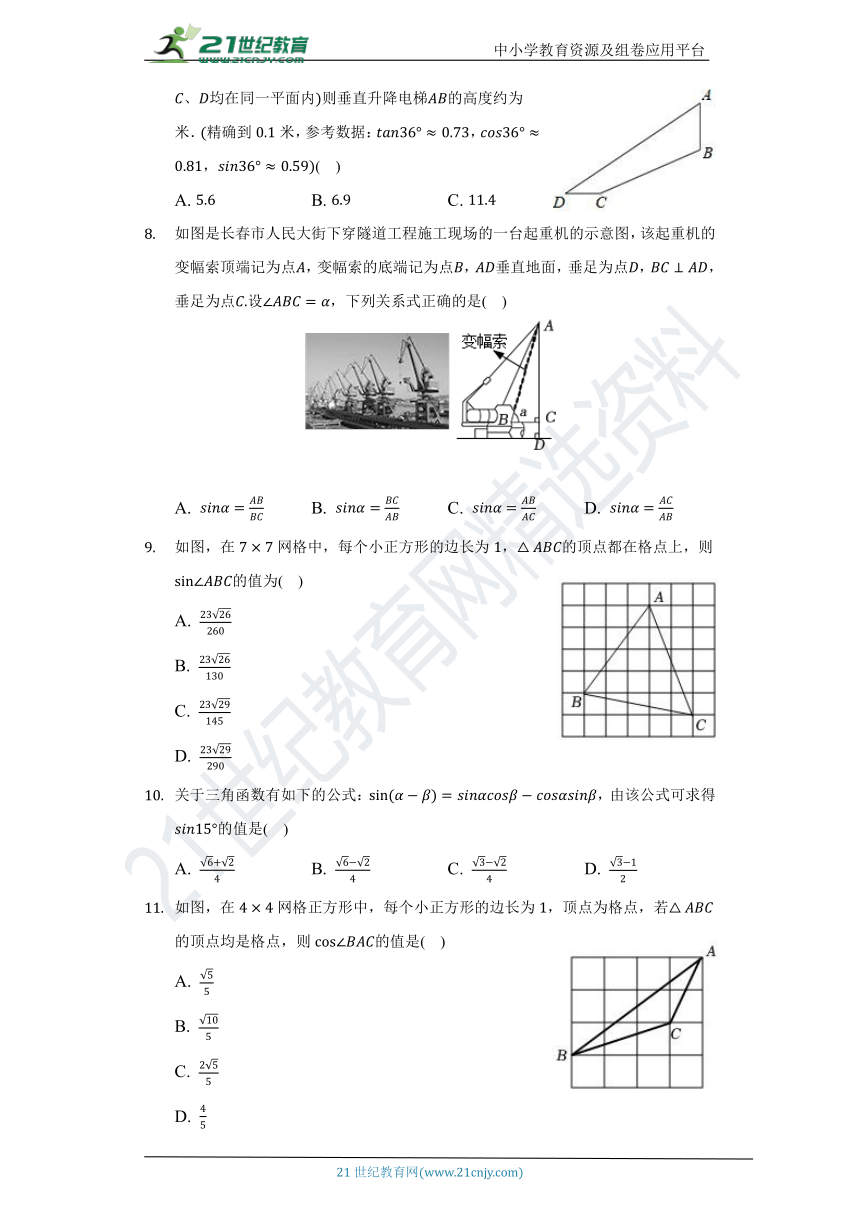
某游乐场新推出了一个“极速飞车”的项目.项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯自由上下选择项目难度.其中斜坡轨道的坡度或坡比为:,米,米,,其中点、、、均在同一平面内则垂直升降电梯的高度约为米.精确到米,参考数据:,,( )
A. B. C. D.
如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点,变幅索的底端记为点,垂直地面,垂足为点,,垂足为点设,下列关系式正确的是( )
A. B. C. D.
如图,在网格中,每个小正方形的边长为,的顶点都在格点上,则的值为( )
A.
B.
C.
D.
关于三角函数有如下的公式:,由该公式可求得的值是( )
A. B. C. D.
如图,在网格正方形中,每个小正方形的边长为,顶点为格点,若的顶点均是格点,则的值是( )
A.
B.
C.
D.
如图,小亮为了测量校园里教学楼的高度,将测角仪竖直放置在与教学楼水平距离为的地面上,若测角仪的高度是测得教学楼的顶部处的仰角为则教学楼的高度是( )
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
计算:______.
在锐角中,若,则的度数是______度.
如图,在高出海平面的悬崖顶处,观测海平面上一艘小船,并测得它的俯角为,则船与观测者之间的水平距离____.
如图,在边长相同的小正方形组成的网格中,点、、都在这些小正方形的顶点上,那么的值为______.
三、解答题(本大题共9小题,共72分)
计算:.
计算:;
解不等式组.
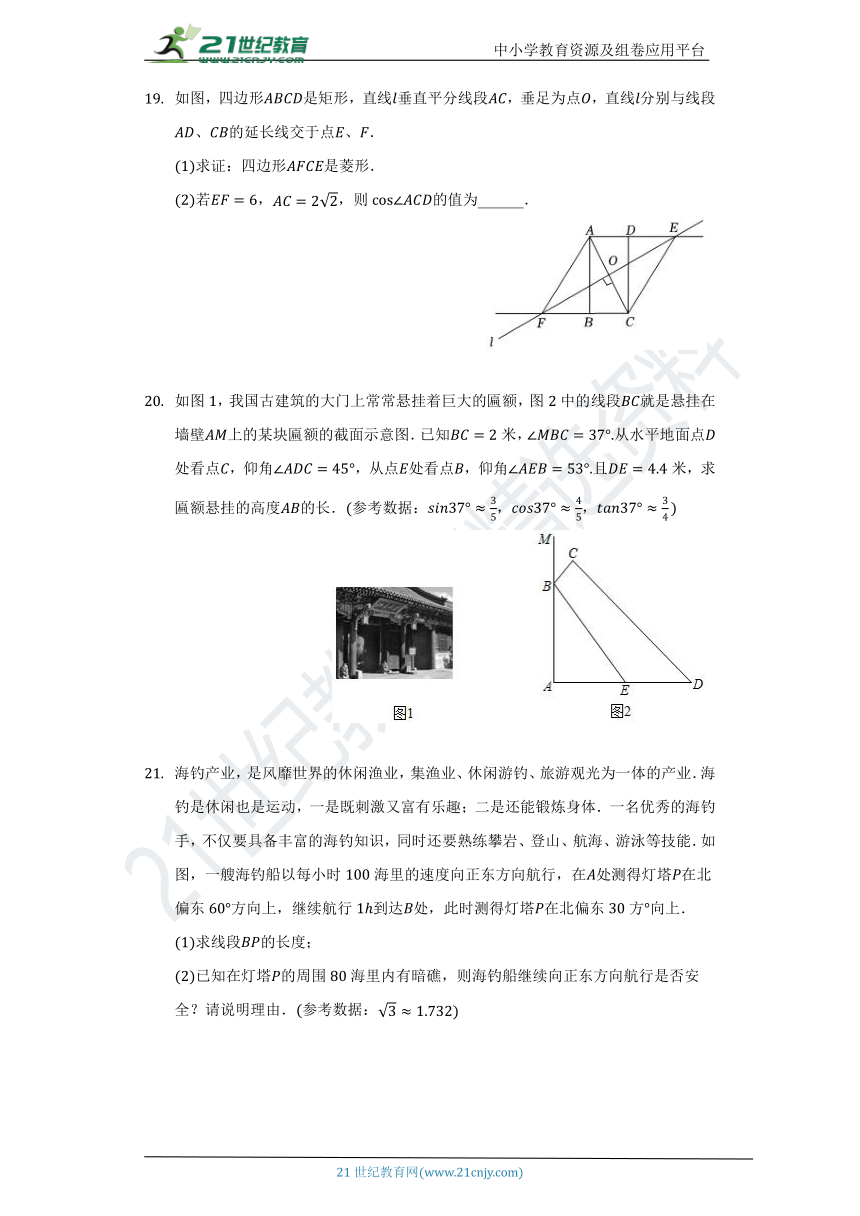
如图,四边形是矩形,直线垂直平分线段,垂足为点,直线分别与线段、的延长线交于点、.
求证:四边形是菱形.
若,,则的值为______.
如图,我国古建筑的大门上常常悬挂着巨大的匾额,图中的线段就是悬挂在墙壁上的某块匾额的截面示意图.已知米,从水平地面点处看点,仰角,从点处看点,仰角且米,求匾额悬挂的高度的长.参考数据:,,
海钓产业,是风靡世界的休闲渔业,集渔业、休闲游钓、旅游观光为一体的产业.海钓是休闲也是运动,一是既刺激又富有乐趣;二是还能锻炼身体.一名优秀的海钓手,不仅要具备丰富的海钓知识,同时还要熟练攀岩、登山、航海、游泳等技能.如图,一艘海钓船以每小时海里的速度向正东方向航行,在处测得灯塔在北偏东方向上,继续航行到达处,此时测得灯塔在北偏东方向上.
求线段的长度;
已知在灯塔的周围海里内有暗礁,则海钓船继续向正东方向航行是否安全?请说明理由.参考数据:
如图,在四边形中,,,,,,点是的中点,联结.
求线段的长;
求的正切值.
如图,某小区的物业楼上悬挂一块高为的广告牌,即小奇和小妙要测量广告牌的底部点到地面的距离.测角仪支架高,小奇在处测得广告牌底部点的仰角为,小妙在处测得广告牌顶部点的仰角为,,请根据相关测量信息,求出广告牌底部点到地面的距离的长.图中点,,,,,,在同一平面内.参考数据:,,
如图所示,在矩形中,点在线段上,点在线段的延长线上,连接交线段于点,连接,若.
求证:四边形是平行四边形;
若,求线段的长度.
小红和小明家分别住在某坡地公园左右两侧同一水平面的、两处,步道正好连接了坡地公园顶部处的平台,周末两人为尽快完成一项共同的工作,决定爬坡到公园坡顶的平台处平台间距离忽略不计商量具体情况,已知两人同时从自己家出门,结果又同时到达了坡地公园顶部处.经了解,小红家所在水平面与坡面的夹角为即,小明家所在水平面与坡面的夹角为即,已知小明步行速度是米秒,求小红的步行速度.参考数据:,,计算结果保留一位小数
答案和解析
1.【答案】
【解析】解:由勾股定理得,则.
2.【答案】
【解析】解:,即,
,
或舍去,
.
故选:.
根据同一锐角的正弦与余弦的平方和是,即可求解.
此题主要考查了同角的三角函数,关键是掌握同一锐角的正弦与余弦之间的关系:对任一锐角,都有.
3.【答案】
【解析】
【分析】
本题主要考查了锐角三角函数的定义,属于基础题.
根据锐角三角函数的定义,进行判断,就可以解决问题.
【解答】
解:中,,、、所对的边分别为、、,
,即,故A选项不成立,选项成立;
,即,故C选项不成立,选项不成立.
故选:.
4.【答案】
【解析】解:、原式,符合题意;
B、原式,不符合题意;
C、原式,不符合题意;
D、原式,不符合题意;
故选:.
A、是分数;
B、底数不为的次幂为,是整数;
C、是整数;
D、是无理数.
主要考查了二次根式的性质与化简、实数、负整数指数幂、零指数幂、特殊角的三角函数值,熟练掌握这几个性质的综合应用是解题关键.
5.【答案】
【解析】
【分析】
本题考查锐角三角函数的定义,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
如图,过点作于利用勾股定理求出即可解决问题.
【解答】
解:如图,过点作于.
在中,,,
,
,
故选:.
6.【答案】
【解析】解:,,,
;
故选:.
根据三角函数的定义即可得出结果.
本题主要考查了解直角三角形、正弦函数的定义;熟练掌握正弦函数的定义是解决问题的关键.
7.【答案】
【解析】
【分析】
本题考查了解直角三角形的应用,利用勾股定理得出,的长是解题关键,又利用了正切函数,线段的和差.
根据勾股定理,可得,的长,根据正切函数,可得的长,再根据线段的和差,可得答案.
【解答】
解:如图
,
由斜坡轨道的坡度或坡比为:,得
::.
设,.
在中,由勾股定理,得
,
即,
解得,
,,
,
由,得
,
解得.
由线段的和差,得
,
故选:.
8.【答案】
【解析】解:在中,,,由锐角三角函数的定义可知,
,
故选:.
根据直角三角形的边角关系进行判断即可.
本题考查解直角三角形的应用,掌握直角三角形的边角关系是正确判断的前提.
9.【答案】
【解析】解:过点作,垂足为,
由图知:,
,
,
,
,
在中,
,
故选:.
过点作,垂足为利用格点先求出、的长,利用的面积求出的长,再计算的正弦值.
本题考查了勾股定理和解直角三角形,利用的面积求出的长是解决本题的关键.
10.【答案】
【解析】解:
,
,
故选:.
根据,代入特殊三角函数值计算即可.
本题主要考查了解直角三角形,掌握特殊三角函数值计算是解题关键.
11.【答案】
【解析】解:延长到,连接,如图:
,,,
,
,
,
故选:.
延长到,连接,由网格可得,即得,可求出答案.
本题考查网格中的锐角三角函数,解题的关键是作辅助线,构造直角三角形.
12.【答案】
【解析】
【分析】
本题考查了解直角三角形,仰角的定义.注意能借助仰角构造直角三角形并解直角三角形是解此题的关键.根据锐角三角函数和直角三角形的性质解答即可.
【解答】
解:过作,则四边形为矩形,
在处测得教学楼顶端的仰角为,
,
,
,
,
故选C.
13.【答案】
【解析】解:原式
.
故答案为:.
直接利用负整数指数幂的性质以及零指数幂的性质、特殊角的三角函数值分别化简,进而合并得出答案.
此题主要考查了实数的运算,正确化简各数是解题关键.
14.【答案】
【解析】解:,
,,
则,,
,,
.
故答案为:.
直接利用非负数的性质以及偶次方的性质,结合特殊角的三角函数值得出,的度数,进而得出答案.
此题主要考查了特殊角的三角函数值、非负数的性质,正确记忆特殊角的三角函数值是解题关键.
15.【答案】
【解析】
【分析】
此题主要考查了解直角三角形的应用,根据已知得出是解决问题的关键.根据解直角三角形的应用,测得它的俯角为,得出,整理代入计算即可得出答案.
【解答】
解:在高出海平面米的悬崖顶处,观测海平面上一艘小船,并测得它的俯角为,
,
船与观测者之间的水平距离米.
故答案为.
16.【答案】
【解析】解:如图,过点作于点,
由题意得:
,,,
,
,
,
在中,,
的值为,
故答案为:.
要求的值,想到把放在直角三角形中,所以过点作于点,解直角三角形即可解答.
本题考查了解直角三角形,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
17.【答案】解:
.
【解析】先化简各式,然后再进行计算即可解答.
本题考查了特殊角的三角函数值,零指数幂,实数的运算,有理数的乘方,绝对值,准确熟练地化简各式是解题的关键.
18.【答案】解:
;
,
解不等式得:,
解不等式得:,
原不等式组的解集为:.
【解析】先化简各式,然后再进行计算即可解答;
按照解一元一次不等式组的步骤,进行计算即可解答.
本题考查了实数的运算,零指数幂,负整数指数幂,特殊角的三角函数值,解一元一次不等式组,准确熟练地进行计算是解题的关键.
19.【答案】
【解析】证明:四边形为矩形,
,
,
直线垂直平分线段,垂足为点,直线分别与线段、的延长线交于点、,
,,,,,
在和中,
,
≌,
,
,
四边形是菱形;
解:四边形是菱形,,,
,,
在中,由勾股定理可得:
,
四边形为矩形,四边形是菱形,
,
,
,
故答案为:.
根据矩形的性质得出,求出,根据线段垂直平分线得出,,,,,证明≌,根据全等三角形的性质得出,求出即可;
根据菱形的性质得出,,,根据勾股定理求出,求出,解直角三角形即可.
本题考查勾股定理,解直角三角形,菱形的判定和性质,矩形的性质,线段垂直平分线等知识点,解题的关键是熟练掌握菱形的判定和性质,矩形的性质,解直角三角形等知识点并综合运用.
20.【答案】解:过点作,,垂足为、,如图所示:
在中,
米,
米
在中,
,
,
,
即:,
解得,米
答:匾额悬挂的高度的长约为米.
【解析】通过作垂线构造直角三角形,在中,求出、,在中用的代数式表示,再根据得出,列方程求解即可.
考查直角三角形的边角关系,通过作垂线构造直角三角形,利用锐角三角函数表示边,再利用各条边之间的关系,列方程求解是解决问题的常用方法.
21.【答案】解:过点作,交的延长线于点.
则,,海里,
设海里,
海里,
在中,,
解得,
在中,,
解得,
海里,
海里.
线段的长度为海里.
由可知,海里,
,
海钓船继续向正东方向航行是安全的.
【解析】过点作,交的延长线于点设海里,在中,,解得,在中,,解得,则海里.
求出的长,与比较,即可得出结论.
本题考查解直角三角形的应用方向角问题,熟练掌握锐角三角函数的定义是解答本题的关键.
22.【答案】解:过点作于,
则,
,,
四边形为矩形,
,,
在中,,
则,
;
过点作于,
则,
点是的中点,
,,
,
.
【解析】过点作于,根据矩形的性质得到,,根据正切的定义求出,计算即可;
过点作于,根据三角形中位线定理求出、,进而求出,根据正切的定义计算,得到答案.
本题考查的是直角梯形、解直角三角形、三角形中位线定理,掌握正切的定义是解题的关键.
23.【答案】解:过点作.
则点,,在同一条直线上,,,,,
设,则,
,,
在中,,
解得,
,,
.
广告牌底部点到地面的距离的长约为.
【解析】过点作设,则,,,在中,,解得,再根据可得出答案.
本题考查解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数的定义是解答本题的关键.
24.【答案】证明:四边形是矩形,
,
又,
四边形是平行四边形;
四边形是平行四边形,
,
,
,
,
又,
.
【解析】由矩形的性质可得,可得结论;
由平行四边形的性质可得,可证,由锐角三角函数可求解.
本题考查了矩形的性质,平行四边形的判定和性质,锐角三角函数等知识,掌握平行四边形的判定方法是解题的关键.
25.【答案】解:过点作于,
设小红的步行速度为米秒,
在中,,
则,
在中,,
则,
由题意得:,即,
解得:,
答:小红的步行速度约为米秒.
【解析】过点作于,根据直角三角形的性质分别用表示出、,根据题意列式计算即可.
本题考查的是解直角三角形的应用坡度坡角问题,掌握直角三角形的性质是解题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
沪科版初中数学九年级上册第23章《解直角三角形》单元测试卷
考试范围:第23章;考试时间:120分钟;总分:120分
学校:___________姓名:___________班级:___________考号:___________
第I卷(选择题)
一、选择题(本大题共12小题,共36分)
在中,,,,则的值是( )
A. B. C. D.
在中,,,则( )
A. B. C. D.
如图,在中,,设,,所对的边分别为,,,则( )
A.
B.
C.
D.
下列各式中,运算结果是分数的是( )
A. B. C. D.
如图,在的正方形网格中,每个小正方形的边长都是,的顶点都在这些小正方形的顶点上,那么的值为( )
A.
B.
C.
D.
在中,,,,则长是( )
A. B. C. D.
某游乐场新推出了一个“极速飞车”的项目.项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯自由上下选择项目难度.其中斜坡轨道的坡度或坡比为:,米,米,,其中点、、、均在同一平面内则垂直升降电梯的高度约为米.精确到米,参考数据:,,( )
A. B. C. D.
如图是长春市人民大街下穿隧道工程施工现场的一台起重机的示意图,该起重机的变幅索顶端记为点,变幅索的底端记为点,垂直地面,垂足为点,,垂足为点设,下列关系式正确的是( )
A. B. C. D.
如图,在网格中,每个小正方形的边长为,的顶点都在格点上,则的值为( )
A.
B.
C.
D.
关于三角函数有如下的公式:,由该公式可求得的值是( )
A. B. C. D.
如图,在网格正方形中,每个小正方形的边长为,顶点为格点,若的顶点均是格点,则的值是( )
A.
B.
C.
D.
如图,小亮为了测量校园里教学楼的高度,将测角仪竖直放置在与教学楼水平距离为的地面上,若测角仪的高度是测得教学楼的顶部处的仰角为则教学楼的高度是( )
A.
B.
C.
D.
第II卷(非选择题)
二、填空题(本大题共4小题,共12分)
计算:______.
在锐角中,若,则的度数是______度.
如图,在高出海平面的悬崖顶处,观测海平面上一艘小船,并测得它的俯角为,则船与观测者之间的水平距离____.
如图,在边长相同的小正方形组成的网格中,点、、都在这些小正方形的顶点上,那么的值为______.
三、解答题(本大题共9小题,共72分)
计算:.
计算:;
解不等式组.
如图,四边形是矩形,直线垂直平分线段,垂足为点,直线分别与线段、的延长线交于点、.
求证:四边形是菱形.
若,,则的值为______.
如图,我国古建筑的大门上常常悬挂着巨大的匾额,图中的线段就是悬挂在墙壁上的某块匾额的截面示意图.已知米,从水平地面点处看点,仰角,从点处看点,仰角且米,求匾额悬挂的高度的长.参考数据:,,
海钓产业,是风靡世界的休闲渔业,集渔业、休闲游钓、旅游观光为一体的产业.海钓是休闲也是运动,一是既刺激又富有乐趣;二是还能锻炼身体.一名优秀的海钓手,不仅要具备丰富的海钓知识,同时还要熟练攀岩、登山、航海、游泳等技能.如图,一艘海钓船以每小时海里的速度向正东方向航行,在处测得灯塔在北偏东方向上,继续航行到达处,此时测得灯塔在北偏东方向上.
求线段的长度;
已知在灯塔的周围海里内有暗礁,则海钓船继续向正东方向航行是否安全?请说明理由.参考数据:
如图,在四边形中,,,,,,点是的中点,联结.
求线段的长;
求的正切值.
如图,某小区的物业楼上悬挂一块高为的广告牌,即小奇和小妙要测量广告牌的底部点到地面的距离.测角仪支架高,小奇在处测得广告牌底部点的仰角为,小妙在处测得广告牌顶部点的仰角为,,请根据相关测量信息,求出广告牌底部点到地面的距离的长.图中点,,,,,,在同一平面内.参考数据:,,
如图所示,在矩形中,点在线段上,点在线段的延长线上,连接交线段于点,连接,若.
求证:四边形是平行四边形;
若,求线段的长度.
小红和小明家分别住在某坡地公园左右两侧同一水平面的、两处,步道正好连接了坡地公园顶部处的平台,周末两人为尽快完成一项共同的工作,决定爬坡到公园坡顶的平台处平台间距离忽略不计商量具体情况,已知两人同时从自己家出门,结果又同时到达了坡地公园顶部处.经了解,小红家所在水平面与坡面的夹角为即,小明家所在水平面与坡面的夹角为即,已知小明步行速度是米秒,求小红的步行速度.参考数据:,,计算结果保留一位小数
答案和解析
1.【答案】
【解析】解:由勾股定理得,则.
2.【答案】
【解析】解:,即,
,
或舍去,
.
故选:.
根据同一锐角的正弦与余弦的平方和是,即可求解.
此题主要考查了同角的三角函数,关键是掌握同一锐角的正弦与余弦之间的关系:对任一锐角,都有.
3.【答案】
【解析】
【分析】
本题主要考查了锐角三角函数的定义,属于基础题.
根据锐角三角函数的定义,进行判断,就可以解决问题.
【解答】
解:中,,、、所对的边分别为、、,
,即,故A选项不成立,选项成立;
,即,故C选项不成立,选项不成立.
故选:.
4.【答案】
【解析】解:、原式,符合题意;
B、原式,不符合题意;
C、原式,不符合题意;
D、原式,不符合题意;
故选:.
A、是分数;
B、底数不为的次幂为,是整数;
C、是整数;
D、是无理数.
主要考查了二次根式的性质与化简、实数、负整数指数幂、零指数幂、特殊角的三角函数值,熟练掌握这几个性质的综合应用是解题关键.
5.【答案】
【解析】
【分析】
本题考查锐角三角函数的定义,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
如图,过点作于利用勾股定理求出即可解决问题.
【解答】
解:如图,过点作于.
在中,,,
,
,
故选:.
6.【答案】
【解析】解:,,,
;
故选:.
根据三角函数的定义即可得出结果.
本题主要考查了解直角三角形、正弦函数的定义;熟练掌握正弦函数的定义是解决问题的关键.
7.【答案】
【解析】
【分析】
本题考查了解直角三角形的应用,利用勾股定理得出,的长是解题关键,又利用了正切函数,线段的和差.
根据勾股定理,可得,的长,根据正切函数,可得的长,再根据线段的和差,可得答案.
【解答】
解:如图
,
由斜坡轨道的坡度或坡比为:,得
::.
设,.
在中,由勾股定理,得
,
即,
解得,
,,
,
由,得
,
解得.
由线段的和差,得
,
故选:.
8.【答案】
【解析】解:在中,,,由锐角三角函数的定义可知,
,
故选:.
根据直角三角形的边角关系进行判断即可.
本题考查解直角三角形的应用,掌握直角三角形的边角关系是正确判断的前提.
9.【答案】
【解析】解:过点作,垂足为,
由图知:,
,
,
,
,
在中,
,
故选:.
过点作,垂足为利用格点先求出、的长,利用的面积求出的长,再计算的正弦值.
本题考查了勾股定理和解直角三角形,利用的面积求出的长是解决本题的关键.
10.【答案】
【解析】解:
,
,
故选:.
根据,代入特殊三角函数值计算即可.
本题主要考查了解直角三角形,掌握特殊三角函数值计算是解题关键.
11.【答案】
【解析】解:延长到,连接,如图:
,,,
,
,
,
故选:.
延长到,连接,由网格可得,即得,可求出答案.
本题考查网格中的锐角三角函数,解题的关键是作辅助线,构造直角三角形.
12.【答案】
【解析】
【分析】
本题考查了解直角三角形,仰角的定义.注意能借助仰角构造直角三角形并解直角三角形是解此题的关键.根据锐角三角函数和直角三角形的性质解答即可.
【解答】
解:过作,则四边形为矩形,
在处测得教学楼顶端的仰角为,
,
,
,
,
故选C.
13.【答案】
【解析】解:原式
.
故答案为:.
直接利用负整数指数幂的性质以及零指数幂的性质、特殊角的三角函数值分别化简,进而合并得出答案.
此题主要考查了实数的运算,正确化简各数是解题关键.
14.【答案】
【解析】解:,
,,
则,,
,,
.
故答案为:.
直接利用非负数的性质以及偶次方的性质,结合特殊角的三角函数值得出,的度数,进而得出答案.
此题主要考查了特殊角的三角函数值、非负数的性质,正确记忆特殊角的三角函数值是解题关键.
15.【答案】
【解析】
【分析】
此题主要考查了解直角三角形的应用,根据已知得出是解决问题的关键.根据解直角三角形的应用,测得它的俯角为,得出,整理代入计算即可得出答案.
【解答】
解:在高出海平面米的悬崖顶处,观测海平面上一艘小船,并测得它的俯角为,
,
船与观测者之间的水平距离米.
故答案为.
16.【答案】
【解析】解:如图,过点作于点,
由题意得:
,,,
,
,
,
在中,,
的值为,
故答案为:.
要求的值,想到把放在直角三角形中,所以过点作于点,解直角三角形即可解答.
本题考查了解直角三角形,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
17.【答案】解:
.
【解析】先化简各式,然后再进行计算即可解答.
本题考查了特殊角的三角函数值,零指数幂,实数的运算,有理数的乘方,绝对值,准确熟练地化简各式是解题的关键.
18.【答案】解:
;
,
解不等式得:,
解不等式得:,
原不等式组的解集为:.
【解析】先化简各式,然后再进行计算即可解答;
按照解一元一次不等式组的步骤,进行计算即可解答.
本题考查了实数的运算,零指数幂,负整数指数幂,特殊角的三角函数值,解一元一次不等式组,准确熟练地进行计算是解题的关键.
19.【答案】
【解析】证明:四边形为矩形,
,
,
直线垂直平分线段,垂足为点,直线分别与线段、的延长线交于点、,
,,,,,
在和中,
,
≌,
,
,
四边形是菱形;
解:四边形是菱形,,,
,,
在中,由勾股定理可得:
,
四边形为矩形,四边形是菱形,
,
,
,
故答案为:.
根据矩形的性质得出,求出,根据线段垂直平分线得出,,,,,证明≌,根据全等三角形的性质得出,求出即可;
根据菱形的性质得出,,,根据勾股定理求出,求出,解直角三角形即可.
本题考查勾股定理,解直角三角形,菱形的判定和性质,矩形的性质,线段垂直平分线等知识点,解题的关键是熟练掌握菱形的判定和性质,矩形的性质,解直角三角形等知识点并综合运用.
20.【答案】解:过点作,,垂足为、,如图所示:
在中,
米,
米
在中,
,
,
,
即:,
解得,米
答:匾额悬挂的高度的长约为米.
【解析】通过作垂线构造直角三角形,在中,求出、,在中用的代数式表示,再根据得出,列方程求解即可.
考查直角三角形的边角关系,通过作垂线构造直角三角形,利用锐角三角函数表示边,再利用各条边之间的关系,列方程求解是解决问题的常用方法.
21.【答案】解:过点作,交的延长线于点.
则,,海里,
设海里,
海里,
在中,,
解得,
在中,,
解得,
海里,
海里.
线段的长度为海里.
由可知,海里,
,
海钓船继续向正东方向航行是安全的.
【解析】过点作,交的延长线于点设海里,在中,,解得,在中,,解得,则海里.
求出的长,与比较,即可得出结论.
本题考查解直角三角形的应用方向角问题,熟练掌握锐角三角函数的定义是解答本题的关键.
22.【答案】解:过点作于,
则,
,,
四边形为矩形,
,,
在中,,
则,
;
过点作于,
则,
点是的中点,
,,
,
.
【解析】过点作于,根据矩形的性质得到,,根据正切的定义求出,计算即可;
过点作于,根据三角形中位线定理求出、,进而求出,根据正切的定义计算,得到答案.
本题考查的是直角梯形、解直角三角形、三角形中位线定理,掌握正切的定义是解题的关键.
23.【答案】解:过点作.
则点,,在同一条直线上,,,,,
设,则,
,,
在中,,
解得,
,,
.
广告牌底部点到地面的距离的长约为.
【解析】过点作设,则,,,在中,,解得,再根据可得出答案.
本题考查解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数的定义是解答本题的关键.
24.【答案】证明:四边形是矩形,
,
又,
四边形是平行四边形;
四边形是平行四边形,
,
,
,
,
又,
.
【解析】由矩形的性质可得,可得结论;
由平行四边形的性质可得,可证,由锐角三角函数可求解.
本题考查了矩形的性质,平行四边形的判定和性质,锐角三角函数等知识,掌握平行四边形的判定方法是解题的关键.
25.【答案】解:过点作于,
设小红的步行速度为米秒,
在中,,
则,
在中,,
则,
由题意得:,即,
解得:,
答:小红的步行速度约为米秒.
【解析】过点作于,根据直角三角形的性质分别用表示出、,根据题意列式计算即可.
本题考查的是解直角三角形的应用坡度坡角问题,掌握直角三角形的性质是解题的关键.
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
