华师大版八年级上册13.2.6 斜边直角边(第6课时 )课件(共22张PPT)
文档属性
| 名称 | 华师大版八年级上册13.2.6 斜边直角边(第6课时 )课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 561.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 16:15:58 | ||
图片预览






文档简介
(共22张PPT)
第13章 全等三角形
13.2 全等三角形
第5课时 全等三角形的判定-斜边直角边
学习目标
1.掌握根据已知条件画直角三角形的方法;
2.掌握判定三角形全等的H.L.定理;(重点)
3.能够运用三角形全等的判定方法进行证明和计算. (难点)
复习提问
一般证明两个三角形全等有哪些方法
新课导入
1.在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为S.A.S.)
2.在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等(简记为A.S.A.)
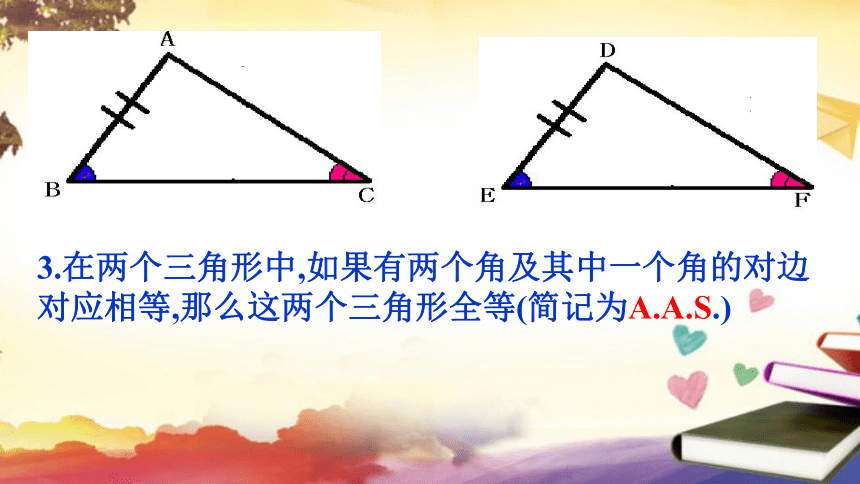
3.在两个三角形中,如果有两个角及其中一个角的对边对应相等,那么这两个三角形全等(简记为A.A.S.)
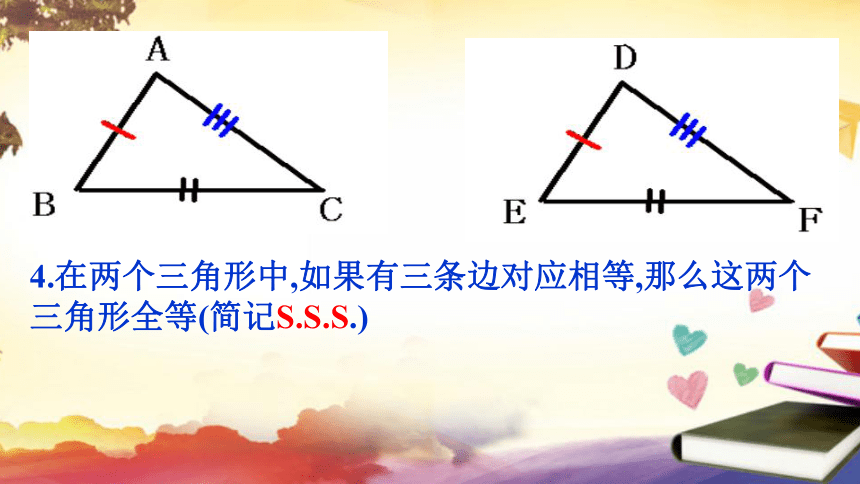
4.在两个三角形中,如果有三条边对应相等,那么这两个三角形全等(简记S.S.S.)
动动手 做一做
画一个Rt△ABC,使得∠C=90°,一直角边BC=2cm,斜边AB=3cm.
知识讲解
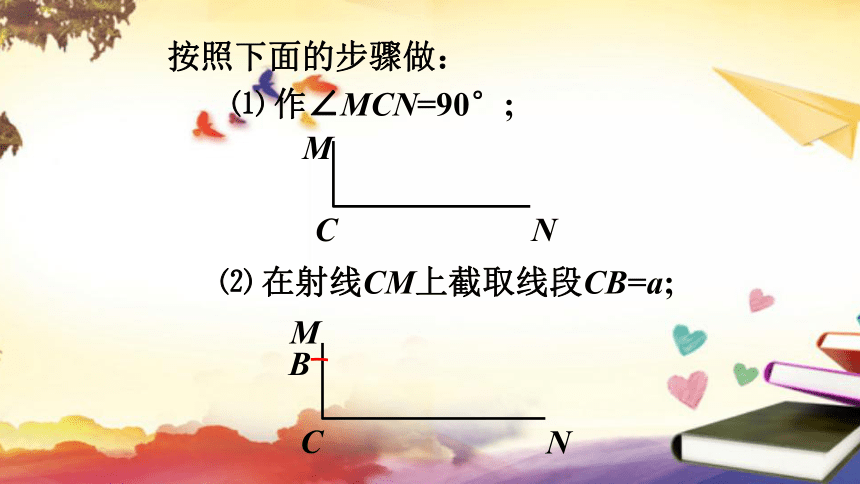
按照下面的步骤做:
⑴ 作∠MCN=90°;
C
M
N
⑵ 在射线CM上截取线段CB=a;
C
M
N
B
⑶ 以B为圆心,AB为半径画弧,交射线CN于点A;
C
M
N
B
A
⑷ 连接AB.
C
M
N
B
A
△ABC就是所求作的三角形.
剪下这个三角形,和其他同学所作的三角形进行比较,它们能重合吗?
重合
文字语言:斜边和一条直角边分别相等的两个直角三角形全等(简写 成“斜边直角边”或“H.L.”).
在Rt△ABC和Rt △ DEF中,
∴ Rt △ABC ≌ Rt △ DEF(HL).
几何语言:
直角三角形全等的判定方法:斜边直角边(H.L.)
AB=DE,
BC=EF (或AC=DF ),
A
B
D
E
F
C
例1 如图,在△ABC和△ABD中,AC⊥BC, AD⊥BD,垂足分别为C,D,BD=AC.
求证:BC=AD.
A
B
D
C
证明:∵ AC⊥BC,AD⊥BD(已知),
∴∠C=∠D=90°.
在Rt△ABC和Rt△BAD中,
∵BD=AC(已知),
AB=BA(公共边),
∴Rt△ABC≌Rt△BAD(H.L.),
∴BC=AD(全等三角形的对应边相等).
证明:
例2 如图,已知AD、AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.
∵AD、AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL),
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL),
∴BD=BF,
∴BD-CD=BF-EF,即BC=BE.
1.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
随堂训练
解:在Rt△ABC和Rt△DEF中,
∵ BC=EF, AC=DF .
∴ Rt△ABC≌Rt△DEF (H.L.).
∴∠ABC=∠DEF(全等三角形对应角相等).
∵ ∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
2. 已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF.
求证:△ABC≌△DEF.
A
B
C
P
D
E
F
Q
∠BAC=∠EDF, AB=DE,∠B=∠E
分析:
Rt△ABP≌Rt△DEQ
AB=DE,AP=DQ
△ABC≌△DEF
A
B
C
P
D
E
F
Q
证明:∵AP、DQ是△ABC和△DEF的高,
∴∠APB=∠DQE=90°.
在Rt△ABP和Rt△DEQ中,
AB=DE,
AP=DQ,
∴Rt△ABP≌Rt△DEQ ,(HL)
∴ ∠B=∠E.
在△ABC和△DEF中,
∠BAC=∠EDF,
AB=DE,
∠B=∠E,
∴△ABC≌△DEF. (ASA)
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF.
求证:△ABC≌△DEF.
A
B
C
P
D
E
F
Q
变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF.
求证:△ABC≌△DEF.
A
B
C
P
D
E
F
Q
变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。
变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF.
求证:△ABC≌△DEF.
A
B
C
P
D
E
F
Q
变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。
变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。
变式3:请你把例题中的∠BAC=∠EDF改为另一个适当条件,使△ABC与△DEF仍能全等。试证明。
课堂小结
直角三角形全等的判定
一般三角形全等的判定
SAS
ASA
AAS
SSS
SAS
ASA
AAS
HL
灵活运用各种方法证明直角三角形全等.
SSS
第13章 全等三角形
13.2 全等三角形
第5课时 全等三角形的判定-斜边直角边
学习目标
1.掌握根据已知条件画直角三角形的方法;
2.掌握判定三角形全等的H.L.定理;(重点)
3.能够运用三角形全等的判定方法进行证明和计算. (难点)
复习提问
一般证明两个三角形全等有哪些方法
新课导入
1.在两个三角形中,如果有两条边及它们的夹角对应相等,那么这两个三角形全等(简记为S.A.S.)
2.在两个三角形中,如果有两个角及它们的夹边对应相等,那么这两个三角形全等(简记为A.S.A.)
3.在两个三角形中,如果有两个角及其中一个角的对边对应相等,那么这两个三角形全等(简记为A.A.S.)
4.在两个三角形中,如果有三条边对应相等,那么这两个三角形全等(简记S.S.S.)
动动手 做一做
画一个Rt△ABC,使得∠C=90°,一直角边BC=2cm,斜边AB=3cm.
知识讲解
按照下面的步骤做:
⑴ 作∠MCN=90°;
C
M
N
⑵ 在射线CM上截取线段CB=a;
C
M
N
B
⑶ 以B为圆心,AB为半径画弧,交射线CN于点A;
C
M
N
B
A
⑷ 连接AB.
C
M
N
B
A
△ABC就是所求作的三角形.
剪下这个三角形,和其他同学所作的三角形进行比较,它们能重合吗?
重合
文字语言:斜边和一条直角边分别相等的两个直角三角形全等(简写 成“斜边直角边”或“H.L.”).
在Rt△ABC和Rt △ DEF中,
∴ Rt △ABC ≌ Rt △ DEF(HL).
几何语言:
直角三角形全等的判定方法:斜边直角边(H.L.)
AB=DE,
BC=EF (或AC=DF ),
A
B
D
E
F
C
例1 如图,在△ABC和△ABD中,AC⊥BC, AD⊥BD,垂足分别为C,D,BD=AC.
求证:BC=AD.
A
B
D
C
证明:∵ AC⊥BC,AD⊥BD(已知),
∴∠C=∠D=90°.
在Rt△ABC和Rt△BAD中,
∵BD=AC(已知),
AB=BA(公共边),
∴Rt△ABC≌Rt△BAD(H.L.),
∴BC=AD(全等三角形的对应边相等).
证明:
例2 如图,已知AD、AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE. 求证:BC=BE.
∵AD、AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL),
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL),
∴BD=BF,
∴BD-CD=BF-EF,即BC=BE.
1.如图,有两个长度相同的滑梯,左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,两个滑梯的倾斜角∠ABC和∠DFE的大小有什么关系?
随堂训练
解:在Rt△ABC和Rt△DEF中,
∵ BC=EF, AC=DF .
∴ Rt△ABC≌Rt△DEF (H.L.).
∴∠ABC=∠DEF(全等三角形对应角相等).
∵ ∠DEF+∠DFE=90°,
∴∠ABC+∠DFE=90°.
2. 已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF.
求证:△ABC≌△DEF.
A
B
C
P
D
E
F
Q
∠BAC=∠EDF, AB=DE,∠B=∠E
分析:
Rt△ABP≌Rt△DEQ
AB=DE,AP=DQ
△ABC≌△DEF
A
B
C
P
D
E
F
Q
证明:∵AP、DQ是△ABC和△DEF的高,
∴∠APB=∠DQE=90°.
在Rt△ABP和Rt△DEQ中,
AB=DE,
AP=DQ,
∴Rt△ABP≌Rt△DEQ ,(HL)
∴ ∠B=∠E.
在△ABC和△DEF中,
∠BAC=∠EDF,
AB=DE,
∠B=∠E,
∴△ABC≌△DEF. (ASA)
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF.
求证:△ABC≌△DEF.
A
B
C
P
D
E
F
Q
变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF.
求证:△ABC≌△DEF.
A
B
C
P
D
E
F
Q
变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。
变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。
已知:如图,在△ABC和△DEF中,AP、DQ分别是高,
并且AB=DE,AP=DQ,∠BAC=∠EDF.
求证:△ABC≌△DEF.
A
B
C
P
D
E
F
Q
变式1:若把∠BAC=∠EDF,改为BC=EF ,△ABC与△DEF全等吗?请说明思路。
变式2:若把∠BAC=∠EDF,改为AC=DF,△ABC与△DEF全等吗?请说明思路。
变式3:请你把例题中的∠BAC=∠EDF改为另一个适当条件,使△ABC与△DEF仍能全等。试证明。
课堂小结
直角三角形全等的判定
一般三角形全等的判定
SAS
ASA
AAS
SSS
SAS
ASA
AAS
HL
灵活运用各种方法证明直角三角形全等.
SSS
