人教A版2019必修第一册4.2 指数函数 学案(Word版含答案)
文档属性
| 名称 | 人教A版2019必修第一册4.2 指数函数 学案(Word版含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 3.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 15:37:13 | ||
图片预览



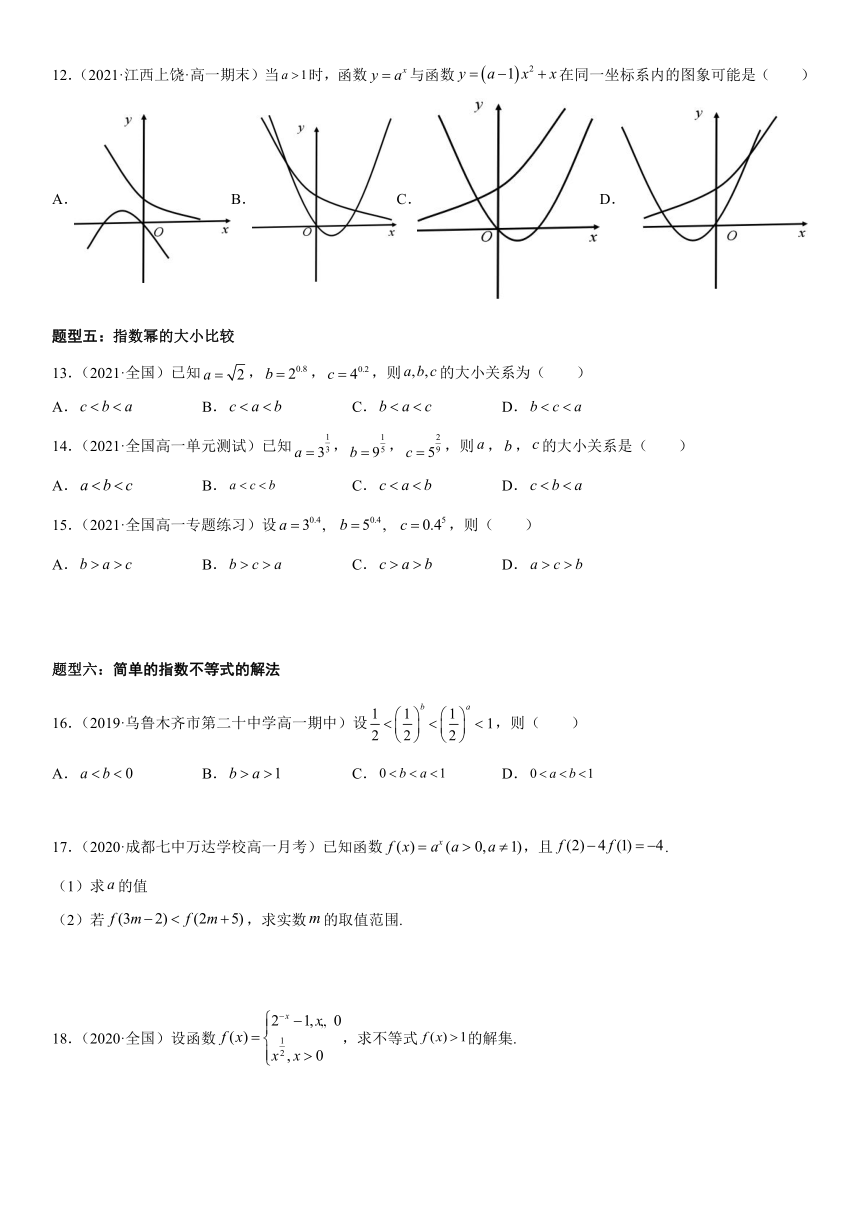

文档简介
4.2指数函数
【考点梳理】
重难点技巧:指数函数的概念
考点一: 指数函数的定义
一般地,函数y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R.
考点二: 两类指数模型
1.y=kax(k>0),当a>1时为指数增长型函数模型.
2.y=kax(k>0),当0 重难点技巧:指数函数的图象和性质
考点三:指数函数的图象和性质
指数函数y=ax(a>0,且a≠1)的图象和性质如下表:
a>1 0图象
定义域 R
值域 (0,+∞)
性质 过定点 过定点(0,1),即x=0时,y=1
函数值的变化 当x>0时,y>1;当x<0时,00时,01
单调性 在R上是增函数 在R上是减函数
考点四:比较幂的大小
(1)对于同底数不同指数的两个幂的大小,利用指数函数的单调性来判断;
(2)对于底数不同指数相同的两个幂的大小,利用幂函数的单调性来判断;
(3)对于底数不同指数也不同的两个幂的大小,则通过中间值来判断.
考点五:解指数方程、不等式
(1)形如af(x)>ag(x)的不等式,可借助y=ax的单调性求解;
(2)形如af(x)>b的不等式,可将b化为以a为底数的指数幂的形式,再借助y=ax的单调性求解;
(3)形如ax>bx的不等式,可借助两函数y=ax,y=bx的图象求解.
考点六 指数型函数的单调性
一般地,有形如y=af(x)(a>0,且a≠1)函数的性质
(1)函数y=af(x)与函数y=f(x)有相同的定义域.
(2)当a>1时,函数y=af(x)与y=f(x)具有相同的单调性;当0【题型归纳】
题型一:指数函数的概念
1.(2020·黔西南州同源中学高一期中)若是指数函数,则有( )
A.或 B.
C. D.且
2.(2020·湖南新宁崀山实验学校高一期中)下列是指数函数的是( )
A. B. C. D.
3.(2020·全国高一专题练习)已知指数函数的图像经过点,那么这个函数也必定经过点( )
A. B. C. D.
题型二:求指数函数的定义域(复合型)
4.(2021·浙江)函数的定义域为( )
A. B. C. D.
5.(2021·内蒙古赤峰·)函数的定义域为( )
A. B. C. D.R
6.(2021·江西高安中学高一月考)函数的定义域是( )
A. B. C. D.
题型三:求指数函数的值域
7.(2020·陕西高一期末)函数的值域是( )
A. B. C. D.
8.(2020·成都市实验外国语学校(西区)高一期中)当时,函数的值域是( )
A. B. C. D.
9.(2020·云南昆明八中高一月考)若函数的定义域为,则该函数的值域是( )
A. B. C. D.
题型四:指数函数的图像问题
10.(2021·全国高一专题练习)函数y=ax-(a>0,且a≠1)的图象可能是( )
A.B.C.D.
11.(2020·乌鲁木齐市第三十一中学高一期末)已知函数的图像过定点P,则P的坐标是( )
A. B.
C. D.
12.(2021·江西上饶·高一期末)当时,函数与函数在同一坐标系内的图象可能是( )
A.B.C.D.
题型五:指数幂的大小比较
13.(2021·全国)已知,,,则的大小关系为( )
A. B. C. D.
14.(2021·全国高一单元测试)已知,,,则,,的大小关系是( )
A. B. C. D.
15.(2021·全国高一专题练习)设,则( )
A. B. C. D.
题型六:简单的指数不等式的解法
16.(2019·乌鲁木齐市第二十中学高一期中)设,则( )
A. B. C. D.
17.(2020·成都七中万达学校高一月考)已知函数,且.
(1)求的值
(2)若,求实数的取值范围.
18.(2020·全国)设函数,求不等式的解集.
题型七:判断复合型指数函数的单调性
19.(2021·罗平县第二中学高二月考)已知函数,则下列说法正确的是( )
A.函数在上是奇函数,也是增函数 B.函数在上是奇函数,也是减函数
C.函数在上是偶函数,也是增函数 D.函数在上是偶函数,也是减函数
20.(2021·湖南郴州·)已知函数,则使得不等式成立的实数的取值范围是( )
A. B. C. D.
21.(2020·河南南阳·高一期末)函数的单调递增区间为( )
A. B. C. D.
题型八:指数函数的最值问题(参数、恒成立)
22.(2021·四川高一开学考试)若对任意的,都有恒成立,则的取值范围为( )
A. B. C. D.
23.(2019·四平市第一高级中学高一期末)已知(且),若有最小值,则实数a的取值范围是( )
A. B. C. D.
24.(2020·江西省临川第二中学)若函数(且)在上的最大值为4,最小值为m ,实数m的值为( )
A. B.或 C. D.或
题型九:指数函数的应用
25.(2021·广东深圳·高一期末)在某个时期,某湖泊中的蓝藻每天以的增长率呈指数增长,已知经过天以后,该湖泊的蓝藻数大约为原来的倍,那么经过天后该湖泊的蓝藻数大约为原来的( )
A.18倍 B.倍 C.倍 D.倍
26.(2021·全国高一专题练习)毛衣柜里的樟脑丸会随着时间挥发而体积缩小,刚放进的新丸体积为,经过天后体积与天数的关系式为.若新丸经过50天后,体积变为,则一个新丸体积变为需经过的时间为( )
A.125天 B.100天 C.75天 D.50天
27.(2021·全国高一专题练习)渔民出海打鱼,为了保证运回鱼的新鲜度(以鱼肉内的三甲胺的多少来确定鱼的新鲜度,三甲胺是一种挥发性碱性氨,是氨的衍生物,它是由细菌分解产生的,三甲胺积聚就表明鱼的新鲜度下降,鱼体开始变质,进而腐败),负被打上船后,要在最短的时间内将其分拣,冷藏,已知某种鱼失去的新鲜度与其出海后时间(分)满足的函数关系式为,若出海后20分这种鱼失去的新鲜度为20%;出海后30分钟,这种鱼失去的新鲜度为40%,那么若不及时处理,打上船的这种鱼大约在多长时间刚好失去50%的新鲜度( )考数据:
A.23分钟 B.33分钟 C.50分钟 D.56分钟
【双基达标】
一、单选题
28.(2020·丽水外国语实验学校高一月考)设,则a,b,c的大小关系是( )
A. B. C. D.
29.(2019·长沙市南雅中学高一月考)下列函数中,在定义域内是单调递增函数的是( )
A.y=|x| B. C. D.
30.(2021·新疆维吾尔自治区阿克苏地区第二中学高一期末)若满足不等式,则函数的值域是( )
A. B. C. D.
31.(2021·江苏高一课时练习)函数,满足对任意,都有成立,则的取值范围是( )
A. B. C. D.
32.(2021·广西高一期中)已知函数,则( )
A.是奇函数,且在上是减函数 B.是偶函数,且在上是减函数
C.是奇函数,且在上是增函数 D.是偶函数,且在上是增函数
33.(2020·全国高一单元测试)函数的图象如图所示,其中,为常数,则下列结论正确的是( )
A., B.,
C., D.,
34.(2021·全国高一课时练习)已知(,且),且,则a的取值范围是( )
A.(0,+∞) B.(1,+∞)
C.(-∞,1) D.(0,1)
35.(2021·全国高一课时练习)已知,,,,则在同一平面直角坐标系内,它们的图象大致为( )
A.B.C.D.
36.(2021·上海)函数且的图像( )
A.与的图像关于轴对称 B.与的图像关于坐标原点对称
C.与的图像关于轴对称 D.与的图像关于坐标原点对称
37.(2021·全国)不等式的解集为( )
A. B. C. D.
【高分突破】
一:单选题
38.(2021·江苏高一课时练习)已知函数的定义域为,则函数的定义域为( )
A. B. C. D.
39.(2021·河南高一期末(文))函数的最小值为( )
A. B.1 C.2 D.
40.(2021·全国高一专题)已知是定义在上的偶函数,那么的最大值是( )
A.1 B. C. D.
41.(2021·全国)镜片的厚度是由镜片的折射率决定,镜片的折射率越高,镜片越薄,同时镜片越轻,也就会带来更为舒适的佩戴体验.某次社会实践活动中,甲、乙、丙三位同学分别制作了三种不同的树脂镜片,折射率分别为,,.则这三种镜片中,制作出最薄镜片和最厚镜片的同学分别为( )
A.甲同学和乙同学 B.丙同学和乙同学
C.乙同学和甲同学 D.丙同学和甲同学
42.(2021·全国高一课时练习)已知函数y=2ax-1+1(a>0且a≠1)恒过定点A(m,n),则m+n=( )
A.1 B.3
C.4 D.2
43.(2021·安徽省太和中学高一月考)函数的部分图象大致为( )
A.B.C.D.
二、多选题
44.(2021·云南省永善县第一中学)已知函数(a,),则下列结论正确的有( )
A.存在实数a,b使得函数为奇函数
B.若函数的图象经过原点,且无限接近直线,则
C.若函数在区间上单调递减,则
D.当时,若对,函数恒成立,则b的取值范围为
45.(2021·全国高一专题练习)已知函数,下面说法正确的有( )
A.的图像关于原点对称 B.的图像关于y轴对称
C.的值域为 D.,且
46.(2021·江苏吴江中学高一期中)已知定义域为的偶函数在上单调递增,且,则下列函数中不符合上述条件的是( )
A. B. C. D.
47.(2021·全国高一专题练习)已知函数,则下面几个结论正确的有( )
A.的图象关于原点对称
B.的图象关于y轴对称
C.的值域为
D.,且恒成立
48.(2021·山东潍坊·高一期末)若函数(且)在上为单调函数,则的值可以是( )
A. B. C. D.2
49.(2021·浙江)高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德 牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设,用表示不超过的最大整数,则称为高斯函数,例如:,.已知函数,函数,以下结论正确的是( )
A.在上是增函数 B.是偶函数
C.是奇函数 D.的值域是
三、填空题
50.(2021·上海金山·高一期末)函数的值域为________.
51.(2021·镇雄县第四中学)已知函数的值域为,则实数的取值范围是___________.
52.(2021·全国高一课时练习)若不等式对一切实数恒成立,则实数的取值范围是________.
53.(2021·全国高一专题练习)在某个时期,某湖泊中的蓝藻每天以的增长率呈指数增长,已知经过天以后,该湖泊的蓝藻数大约为原来的倍,那么经过天后该湖泊的蓝藻数大约为原来的_____
54.(2021·全国高一课时练习)函数f(x)=,若有f(a)+f(a-2)>4,则a的取值范围是________.
四、解答题
55.(2021·黑龙江齐齐哈尔市·齐齐哈尔中学高一期中)已知函数.
(1)在平面直角坐标系中,画出函数的简图;
(2)根据函数的图象,写出函数的单调区间﹔
(3)若,求实数的值.
56.(2021·全国高一专题练习)已知函数是R上的奇函数.
(1)求的值;
(2)用定义证明在上为减函数;
(3)若对于任意,不等式恒成立,求实数的取值范围.
57.(2021·河北正定中学)设函数f(x)=ax-a-x(x∈R,a>0且a≠1).
(1)若f(1)<0,求使不等式f(x2+tx)+f(4-x)<0恒成立时实数t的取值范围;
(2)若,g(x)=a2x+a-2x-2mf(x)且g(x)在[1,+∞)上的最小值为-2,求实数m的值.
58.(2021·全国高一课时练习)已知定义在R上的奇函数和偶函数满足且),
(1)若,求.
(2)记,求的最小值.
59.(2021·全国高一专题练习)已知函数
(1)若,求a的值
(2)记在区间上的最小值为
①求的解析式
②若对于恒成立,求k的范围
60.(2021·江苏)已知函数.
(1)解不等式;
(2)若函数在上有零点,求m的取值范围;
(3)若函数,其中为奇函数,为偶函数,若不等式对任意恒成立,求实数a的取值范围.
【答案详解】
1.C
【详解】
因为是指数函数,
所以,解得.
故选:C.
2.D
【详解】
对于选项A:,因为不满足底数且,故不是指数函数,故选项A不正确;
对于选项B:不满足指数函数前系数等于,故不是指数函数,故选项B不正确;
对于选项C:没有指出的范围,当且时才是指数函数,故选项C不正确;
对于选项D:是指数函数,故选项D正确,
故选:D
3.D
【详解】
设,且 即
因为
所以D正确
故选D
4.A
【详解】
由题意,,得,所以.
故选:A
5.A
【详解】
要使函数有意义,必须且只需,解得,
故选:A.
6.A
【详解】
要使函数有意义,则需,
即为,解得,,则定义域为.
故选:A.
7.C
【详解】
因为函数在上单调递增,
所以,
又因为,所以,
即函数的值域是,
故选:C.
8.C
【详解】
因为指数函数在区间上是增函数,所以,
于是即.
故选:C.
9.C
【详解】
令,
因为,则,
又因为为单调递增函数,
所以.
故选:C
10.D
【详解】
当时,为增函数,当时,且,
故A,B 不符合.
当时,为减函数,当时,,故C不符合,D符合.
故选:D.
11.D
【详解】
因时,不论取符合条件的任何实数,所对应函数值均为2,即,均有,
于是得函数的图像过定点,
所以P的坐标是.
故选:D
12.D
【详解】
因为,所以是增函数;排除AB选项;
二次函数开口向上,对称轴,排除C选项;即D正确;
故选:D.
13.B
【详解】
,,
∵递增,且,
∴,即.
故选:B.
14.C
【详解】
∵,,
∴.
故选:C.
15.A
【详解】
因为函数在上的增函数,且,
所以,即
又,所以,
所以.
故选:A.
16.D
【详解】
因为是单调递减函数,
又
所以,
故选:D.
17.(1);(2).
【详解】
(1)由题意,
则,解得
综上所述,结论是:.
(2)由(1)知,则是上的增函数,
因为
则,
解得
综上所述,结论是:
18.
【详解】
解:等价于或,
即或,
或,
∴不等式的解集为.
19.A
【详解】
,故为奇函数,排除C、D;
令,则,又,,
∴,即,即为增函数,排除D.
故选:A
20.B
【详解】
函数,
令,
因为,
所以是偶函数,其图象关于y轴对称,且在上递减,在上递增,
所以的图象关于对称,且在 上递减,在上递增,
若使得不等式成立
则,
即,
解得,
所以实数的取值范围是
故选:B
21.A
【详解】
因为函数的单调递增区间为,
所以根据复合函数单调性可知,的单调递增区间为
故选:A
22.B
【详解】
由得,
,所以的最小值为,
所以,.
故选:B.
23.B
【详解】
由题意分情况讨论:
①当时,
当时,单调递增,此时;
当时, 单调递减;
,单调递增,
故时,的最小值为,
故若有最小值,则;
② 当时,
当时,单调递减,此时;
当时,单调递增,此时,
故若有最小值,则,解得,
综上实数的取值范围是
故选:B
24.D
【详解】
当时,在单调递增,所以,解得:,所以此时,,
当时,在单调递减,所以,解得:
,所以此时,,
所以m的值为或,
故选:D
25.C
【详解】
某湖泊中的蓝藻每天以的增长率呈指数增长,经过30天以后,该湖泊的蓝藻数大约为原来的6倍,
设湖泊中原来蓝藻数量为,则,
经过60天后该湖泊的蓝藻数量为:
经过60天后该湖泊的蓝藻数大约为原来的36倍.
故选:C.
26.C
【详解】
解析:由题意知,当时,有.
即,得.
所以当时,有.
即,得.
所以.
故选:C
27.B
【详解】
由题意可得,解得.
故.
令,即,
两边同时取对数,故分钟
故选:B
28.B
【详解】
解:∵,
函数是减函数,,∴,∴.
又函数是R上的增函数,,∴,即,
综上可得,,
故选:B.
29.D
【详解】
,在定义域内都不是单调递增的,不满足题意,
在定义域上单调递减,不满足题意,
在定义域上单调递增,满足题意,.
故选:D
30.B
【详解】
由可得,
因为在上单调递增,
所以即,解得:,
所以,即函数的值域是,
故选:B.
31.C
解:满足对任意,都有成立,
在上是减函数,
因为
,解得,
的取值范围是.
故选:.
32.C
【详解】
解:,定义域为
,
为奇函数,故可排除,;
又在定义域上单调递增,在定义域上单调递减,
在上是增函数,符合题意,可排除;
故选:.
33.A
【详解】
由,可得,
因为由图像可知函数是减函数,所以,所以,
因为,
所以,所以,
故选:A
34.D
【详解】
由,且,排除AC;
∵,
当时,为单调递减函数,∴,与已知矛盾矛盾,故B错误;
当时,为单调递增函数,∴,符合题意.
故选:D.
35.A
【详解】
与是增函数,与是减函数,在第一象限内作直线,
该直线与四条曲线交点的纵坐标的大小对应各底数的大小,易知:选A.
故选:A
36.D
【详解】
函数y=a-x是把y=-ax中的x换成-x,把y换成-y,
所以两个函数的图像关于原点对称,
故选:D.
37.D
【详解】
当时,由,则,
即,解得或,
所以或,
又因,所以;
当时,,
由,即,即,
即,解得,
所以,
又因,所以,
综上所述:不等式的解集为.
故选:D.
38.B
【详解】
要使有意义,则,解得,所以函数的定义域为.
故选:B.
39.D
【详解】
令,则,
故原函数化为,
当时,可得最小值为.
故选:D.
40.D
【详解】
解:根据题意,是定义在,上的偶函数,则有,则,
同时,即,则有,必有,
则,其定义域为,,
则,设,若,则有,
在区间,上,且为减函数,
在区间,上为增函数,
则在,上为减函数,其最大值为,
故选:.
41.C
【详解】
,.∵.∴.
又∵,,∴.
∴有.
又因为镜片折射率越高,镜片越薄,故甲同学创作的镜片最厚,乙同学创作的镜片最薄.
故选:C.
42.C
【详解】
由题意知,当x=1时,y=3,故A(1,3),m+n=4,
故选:C.
43.A
【详解】
由,得.
当时,,
所以B,D错误;
当时,,所以C错误.
故选:.
44.ABC
【详解】
A.当时,,此时为奇函数,故选项A正确;
B.为偶函数,在区间上为减函数,图象过点,且以x轴为渐近线.
若函数的图象经过原点,且渐近线为时,,,选项B正确;
C.因为偶函数,在区间上为减函数,
故若函数在区间上单调递减,则,选项C正确:
D.当时,,,若恒成立,得,即,而,此时,,
当时,,得,若恒成立,得,
当时,,得,
若恒成立,得,即,而,因此得,
选项D不正确,
故选:ABC.
45.ACD
【详解】
的定义域为关于原点对称,
,所以是奇函数,图象关于原点对称,
故选项A正确,选项B不正确;
,因为,所以,所以,
,所以,可得的值域为,故选项C正确;
设任意的,
则,
因为,,,所以,
即,所以,故选项D正确;
故选:ACD
46.ABD
【详解】
A:由在定义域上的值域为,显然不符合,;
B:在定义域上单调递增,但在定义域上有,即为奇函数,不符合题设函数性质;
C:在定义域上是偶函数,在上单调递增,且,符合题设函数的性质;
D:由幂函数的性质知:在上单调递减,不合题设函数性质;
故选:ABD.
47.ACD
【详解】
对于A,,则,
则为奇函数,故图象关于原点对称,故A正确.
对于B,计算,,故的图象不关于y轴对称,故B错误.
对于C,,,
故,易知:,故的值域为,故C正确.
对于D,,
因为在上为增函数,为上的减函数,
由复合函数的单调性的判断法则可得在上单调递减,
故,且,恒成立,故D正确.
故选:ACD.
48.ABD
【详解】
解:因为函数(且)在上为单调函数,
所以或,解得或,所以满足条件的有ABD;
故选:ABD
49.ACD
【详解】
函数,定义域为R,
又指数函数是单调递增的,可知是单调递减的,取值为,
故是单调递增的,值域为,故A正确;
当时,,当时,,
故的值域是,D正确;
又,故是奇函数,即C正确;
因为,故,,故,即,故不可能是偶函数,B错误.
故选:ACD.
50.
由指数函数的性质知:,
∴.
故答案为:
51.
由题意,的值域为:
要使得:的值域为
必为减函数,因此
可作出函数图象如图,由图象可知解之得.
故答案为:
52.
【详解】
原不等式可变形为,因为指数函数为增函数,
则有,
即对一切实数恒成立.
①当时,,满足题意;
②当时,若二次函数大于0恒成立,则需且,
即且,解得.
综上,实数的取值范围是.
故答案为:
53.36倍
【详解】
某湖泊中的蓝藻每天以的增长率呈指数增长,经过30天以后,该湖泊的蓝藻数大约为原来的6倍,
设湖泊中原来蓝藻数量为,则,
经过60天后该湖泊的蓝藻数量为:
经过60天后该湖泊的蓝藻数大约为原来的36倍.
故答案为:36倍
54.(1,+∞)
【详解】
设F(x)=f(x)-2,则F(x)=,易知F(x)是奇函数,F(x)===1-在R上是增函数,
由f(a)+f(a-2)>4得F(a)+F(a-2)>0,
于是可得F(a)>F(2-a),即a>2-a,解得a>1.
答案:(1,+∞)
55.
解:(1)函数的简图如下:
(2)由图可知,函数的增区间为,减区间为;
(3)由,及函数的单调性可知,
若则实数的值为或.
56.
解:(1)由函数是R上的奇函数知,
即,解得.
(2)由(1)知.
任取,则
因为,所以,所以,
又因为,故,
所以,即
所以在上为减函数.
(3)不等式可化为
因为是奇函数,故
所以不等式可化为
由(2)知在上为减函数,故即
即对于任意,不等式恒成立.
设易知
因此
所以实数的取值范围是.
57.【详解】
(1),即,而,则,解得,显然在上单调递减,
又,于是得在上是奇函数,
从而有等价于,
由原不等式恒成立可得,即恒成立,亦即,解得:,
所以实数的取值范围是:;
(2),即,而,解得:,
所以,
令,显然在上单调递增,则,
,对称轴为,
当时,,解得或(舍),则,
当时,,解得:不符合题意,
综上得,
所以实数m的值为2.
58.(1);(2).
(1)是奇函数,是偶函数,
由,①
得,②
①②得,①②得.
又,,,
.
(2)由(1)可得,故,
由基本不等式可得,
令,则且,设,
当即时,;
当即时,,
故.
59.(1);(2)①;②.
【详解】
(1)
所以;
(2)①,
令,所以,
令或.
当时,;
当时,;
当时,.
所以.
②函数的图象如图所示,
从函数的图象和解析式可以看出函数单调递减,
因为对于恒成立,
所以,
所以.
所以.
60.(1);(2);(3).
解:(1)因为,
所以
设,,
原不等式可化为,
整理可得,解得,
即,解得,
所以不等式的解集为.
(2)设,由可得,
则,
令,
由二次函数的知识可得,当时,,当时,,
故函数的值域为,
函数有零点等价于方程有解,等价于在的值域内,
故的取值范围为
(3)由题意得解得
即,对任意恒成立,
又时,令,则,
因为在上单调递增,
当时,有最大值,
所以
试卷第1页,共3页
【考点梳理】
重难点技巧:指数函数的概念
考点一: 指数函数的定义
一般地,函数y=ax(a>0,且a≠1)叫做指数函数,其中x是自变量,函数的定义域是R.
考点二: 两类指数模型
1.y=kax(k>0),当a>1时为指数增长型函数模型.
2.y=kax(k>0),当0
考点三:指数函数的图象和性质
指数函数y=ax(a>0,且a≠1)的图象和性质如下表:
a>1 0
定义域 R
值域 (0,+∞)
性质 过定点 过定点(0,1),即x=0时,y=1
函数值的变化 当x>0时,y>1;当x<0时,0
单调性 在R上是增函数 在R上是减函数
考点四:比较幂的大小
(1)对于同底数不同指数的两个幂的大小,利用指数函数的单调性来判断;
(2)对于底数不同指数相同的两个幂的大小,利用幂函数的单调性来判断;
(3)对于底数不同指数也不同的两个幂的大小,则通过中间值来判断.
考点五:解指数方程、不等式
(1)形如af(x)>ag(x)的不等式,可借助y=ax的单调性求解;
(2)形如af(x)>b的不等式,可将b化为以a为底数的指数幂的形式,再借助y=ax的单调性求解;
(3)形如ax>bx的不等式,可借助两函数y=ax,y=bx的图象求解.
考点六 指数型函数的单调性
一般地,有形如y=af(x)(a>0,且a≠1)函数的性质
(1)函数y=af(x)与函数y=f(x)有相同的定义域.
(2)当a>1时,函数y=af(x)与y=f(x)具有相同的单调性;当0
题型一:指数函数的概念
1.(2020·黔西南州同源中学高一期中)若是指数函数,则有( )
A.或 B.
C. D.且
2.(2020·湖南新宁崀山实验学校高一期中)下列是指数函数的是( )
A. B. C. D.
3.(2020·全国高一专题练习)已知指数函数的图像经过点,那么这个函数也必定经过点( )
A. B. C. D.
题型二:求指数函数的定义域(复合型)
4.(2021·浙江)函数的定义域为( )
A. B. C. D.
5.(2021·内蒙古赤峰·)函数的定义域为( )
A. B. C. D.R
6.(2021·江西高安中学高一月考)函数的定义域是( )
A. B. C. D.
题型三:求指数函数的值域
7.(2020·陕西高一期末)函数的值域是( )
A. B. C. D.
8.(2020·成都市实验外国语学校(西区)高一期中)当时,函数的值域是( )
A. B. C. D.
9.(2020·云南昆明八中高一月考)若函数的定义域为,则该函数的值域是( )
A. B. C. D.
题型四:指数函数的图像问题
10.(2021·全国高一专题练习)函数y=ax-(a>0,且a≠1)的图象可能是( )
A.B.C.D.
11.(2020·乌鲁木齐市第三十一中学高一期末)已知函数的图像过定点P,则P的坐标是( )
A. B.
C. D.
12.(2021·江西上饶·高一期末)当时,函数与函数在同一坐标系内的图象可能是( )
A.B.C.D.
题型五:指数幂的大小比较
13.(2021·全国)已知,,,则的大小关系为( )
A. B. C. D.
14.(2021·全国高一单元测试)已知,,,则,,的大小关系是( )
A. B. C. D.
15.(2021·全国高一专题练习)设,则( )
A. B. C. D.
题型六:简单的指数不等式的解法
16.(2019·乌鲁木齐市第二十中学高一期中)设,则( )
A. B. C. D.
17.(2020·成都七中万达学校高一月考)已知函数,且.
(1)求的值
(2)若,求实数的取值范围.
18.(2020·全国)设函数,求不等式的解集.
题型七:判断复合型指数函数的单调性
19.(2021·罗平县第二中学高二月考)已知函数,则下列说法正确的是( )
A.函数在上是奇函数,也是增函数 B.函数在上是奇函数,也是减函数
C.函数在上是偶函数,也是增函数 D.函数在上是偶函数,也是减函数
20.(2021·湖南郴州·)已知函数,则使得不等式成立的实数的取值范围是( )
A. B. C. D.
21.(2020·河南南阳·高一期末)函数的单调递增区间为( )
A. B. C. D.
题型八:指数函数的最值问题(参数、恒成立)
22.(2021·四川高一开学考试)若对任意的,都有恒成立,则的取值范围为( )
A. B. C. D.
23.(2019·四平市第一高级中学高一期末)已知(且),若有最小值,则实数a的取值范围是( )
A. B. C. D.
24.(2020·江西省临川第二中学)若函数(且)在上的最大值为4,最小值为m ,实数m的值为( )
A. B.或 C. D.或
题型九:指数函数的应用
25.(2021·广东深圳·高一期末)在某个时期,某湖泊中的蓝藻每天以的增长率呈指数增长,已知经过天以后,该湖泊的蓝藻数大约为原来的倍,那么经过天后该湖泊的蓝藻数大约为原来的( )
A.18倍 B.倍 C.倍 D.倍
26.(2021·全国高一专题练习)毛衣柜里的樟脑丸会随着时间挥发而体积缩小,刚放进的新丸体积为,经过天后体积与天数的关系式为.若新丸经过50天后,体积变为,则一个新丸体积变为需经过的时间为( )
A.125天 B.100天 C.75天 D.50天
27.(2021·全国高一专题练习)渔民出海打鱼,为了保证运回鱼的新鲜度(以鱼肉内的三甲胺的多少来确定鱼的新鲜度,三甲胺是一种挥发性碱性氨,是氨的衍生物,它是由细菌分解产生的,三甲胺积聚就表明鱼的新鲜度下降,鱼体开始变质,进而腐败),负被打上船后,要在最短的时间内将其分拣,冷藏,已知某种鱼失去的新鲜度与其出海后时间(分)满足的函数关系式为,若出海后20分这种鱼失去的新鲜度为20%;出海后30分钟,这种鱼失去的新鲜度为40%,那么若不及时处理,打上船的这种鱼大约在多长时间刚好失去50%的新鲜度( )考数据:
A.23分钟 B.33分钟 C.50分钟 D.56分钟
【双基达标】
一、单选题
28.(2020·丽水外国语实验学校高一月考)设,则a,b,c的大小关系是( )
A. B. C. D.
29.(2019·长沙市南雅中学高一月考)下列函数中,在定义域内是单调递增函数的是( )
A.y=|x| B. C. D.
30.(2021·新疆维吾尔自治区阿克苏地区第二中学高一期末)若满足不等式,则函数的值域是( )
A. B. C. D.
31.(2021·江苏高一课时练习)函数,满足对任意,都有成立,则的取值范围是( )
A. B. C. D.
32.(2021·广西高一期中)已知函数,则( )
A.是奇函数,且在上是减函数 B.是偶函数,且在上是减函数
C.是奇函数,且在上是增函数 D.是偶函数,且在上是增函数
33.(2020·全国高一单元测试)函数的图象如图所示,其中,为常数,则下列结论正确的是( )
A., B.,
C., D.,
34.(2021·全国高一课时练习)已知(,且),且,则a的取值范围是( )
A.(0,+∞) B.(1,+∞)
C.(-∞,1) D.(0,1)
35.(2021·全国高一课时练习)已知,,,,则在同一平面直角坐标系内,它们的图象大致为( )
A.B.C.D.
36.(2021·上海)函数且的图像( )
A.与的图像关于轴对称 B.与的图像关于坐标原点对称
C.与的图像关于轴对称 D.与的图像关于坐标原点对称
37.(2021·全国)不等式的解集为( )
A. B. C. D.
【高分突破】
一:单选题
38.(2021·江苏高一课时练习)已知函数的定义域为,则函数的定义域为( )
A. B. C. D.
39.(2021·河南高一期末(文))函数的最小值为( )
A. B.1 C.2 D.
40.(2021·全国高一专题)已知是定义在上的偶函数,那么的最大值是( )
A.1 B. C. D.
41.(2021·全国)镜片的厚度是由镜片的折射率决定,镜片的折射率越高,镜片越薄,同时镜片越轻,也就会带来更为舒适的佩戴体验.某次社会实践活动中,甲、乙、丙三位同学分别制作了三种不同的树脂镜片,折射率分别为,,.则这三种镜片中,制作出最薄镜片和最厚镜片的同学分别为( )
A.甲同学和乙同学 B.丙同学和乙同学
C.乙同学和甲同学 D.丙同学和甲同学
42.(2021·全国高一课时练习)已知函数y=2ax-1+1(a>0且a≠1)恒过定点A(m,n),则m+n=( )
A.1 B.3
C.4 D.2
43.(2021·安徽省太和中学高一月考)函数的部分图象大致为( )
A.B.C.D.
二、多选题
44.(2021·云南省永善县第一中学)已知函数(a,),则下列结论正确的有( )
A.存在实数a,b使得函数为奇函数
B.若函数的图象经过原点,且无限接近直线,则
C.若函数在区间上单调递减,则
D.当时,若对,函数恒成立,则b的取值范围为
45.(2021·全国高一专题练习)已知函数,下面说法正确的有( )
A.的图像关于原点对称 B.的图像关于y轴对称
C.的值域为 D.,且
46.(2021·江苏吴江中学高一期中)已知定义域为的偶函数在上单调递增,且,则下列函数中不符合上述条件的是( )
A. B. C. D.
47.(2021·全国高一专题练习)已知函数,则下面几个结论正确的有( )
A.的图象关于原点对称
B.的图象关于y轴对称
C.的值域为
D.,且恒成立
48.(2021·山东潍坊·高一期末)若函数(且)在上为单调函数,则的值可以是( )
A. B. C. D.2
49.(2021·浙江)高斯是德国著名的数学家,近代数学奠基者之一,享有“数学王子”的称号,他和阿基米德 牛顿并列为世界三大数学家,用其名字命名的“高斯函数”为:设,用表示不超过的最大整数,则称为高斯函数,例如:,.已知函数,函数,以下结论正确的是( )
A.在上是增函数 B.是偶函数
C.是奇函数 D.的值域是
三、填空题
50.(2021·上海金山·高一期末)函数的值域为________.
51.(2021·镇雄县第四中学)已知函数的值域为,则实数的取值范围是___________.
52.(2021·全国高一课时练习)若不等式对一切实数恒成立,则实数的取值范围是________.
53.(2021·全国高一专题练习)在某个时期,某湖泊中的蓝藻每天以的增长率呈指数增长,已知经过天以后,该湖泊的蓝藻数大约为原来的倍,那么经过天后该湖泊的蓝藻数大约为原来的_____
54.(2021·全国高一课时练习)函数f(x)=,若有f(a)+f(a-2)>4,则a的取值范围是________.
四、解答题
55.(2021·黑龙江齐齐哈尔市·齐齐哈尔中学高一期中)已知函数.
(1)在平面直角坐标系中,画出函数的简图;
(2)根据函数的图象,写出函数的单调区间﹔
(3)若,求实数的值.
56.(2021·全国高一专题练习)已知函数是R上的奇函数.
(1)求的值;
(2)用定义证明在上为减函数;
(3)若对于任意,不等式恒成立,求实数的取值范围.
57.(2021·河北正定中学)设函数f(x)=ax-a-x(x∈R,a>0且a≠1).
(1)若f(1)<0,求使不等式f(x2+tx)+f(4-x)<0恒成立时实数t的取值范围;
(2)若,g(x)=a2x+a-2x-2mf(x)且g(x)在[1,+∞)上的最小值为-2,求实数m的值.
58.(2021·全国高一课时练习)已知定义在R上的奇函数和偶函数满足且),
(1)若,求.
(2)记,求的最小值.
59.(2021·全国高一专题练习)已知函数
(1)若,求a的值
(2)记在区间上的最小值为
①求的解析式
②若对于恒成立,求k的范围
60.(2021·江苏)已知函数.
(1)解不等式;
(2)若函数在上有零点,求m的取值范围;
(3)若函数,其中为奇函数,为偶函数,若不等式对任意恒成立,求实数a的取值范围.
【答案详解】
1.C
【详解】
因为是指数函数,
所以,解得.
故选:C.
2.D
【详解】
对于选项A:,因为不满足底数且,故不是指数函数,故选项A不正确;
对于选项B:不满足指数函数前系数等于,故不是指数函数,故选项B不正确;
对于选项C:没有指出的范围,当且时才是指数函数,故选项C不正确;
对于选项D:是指数函数,故选项D正确,
故选:D
3.D
【详解】
设,且 即
因为
所以D正确
故选D
4.A
【详解】
由题意,,得,所以.
故选:A
5.A
【详解】
要使函数有意义,必须且只需,解得,
故选:A.
6.A
【详解】
要使函数有意义,则需,
即为,解得,,则定义域为.
故选:A.
7.C
【详解】
因为函数在上单调递增,
所以,
又因为,所以,
即函数的值域是,
故选:C.
8.C
【详解】
因为指数函数在区间上是增函数,所以,
于是即.
故选:C.
9.C
【详解】
令,
因为,则,
又因为为单调递增函数,
所以.
故选:C
10.D
【详解】
当时,为增函数,当时,且,
故A,B 不符合.
当时,为减函数,当时,,故C不符合,D符合.
故选:D.
11.D
【详解】
因时,不论取符合条件的任何实数,所对应函数值均为2,即,均有,
于是得函数的图像过定点,
所以P的坐标是.
故选:D
12.D
【详解】
因为,所以是增函数;排除AB选项;
二次函数开口向上,对称轴,排除C选项;即D正确;
故选:D.
13.B
【详解】
,,
∵递增,且,
∴,即.
故选:B.
14.C
【详解】
∵,,
∴.
故选:C.
15.A
【详解】
因为函数在上的增函数,且,
所以,即
又,所以,
所以.
故选:A.
16.D
【详解】
因为是单调递减函数,
又
所以,
故选:D.
17.(1);(2).
【详解】
(1)由题意,
则,解得
综上所述,结论是:.
(2)由(1)知,则是上的增函数,
因为
则,
解得
综上所述,结论是:
18.
【详解】
解:等价于或,
即或,
或,
∴不等式的解集为.
19.A
【详解】
,故为奇函数,排除C、D;
令,则,又,,
∴,即,即为增函数,排除D.
故选:A
20.B
【详解】
函数,
令,
因为,
所以是偶函数,其图象关于y轴对称,且在上递减,在上递增,
所以的图象关于对称,且在 上递减,在上递增,
若使得不等式成立
则,
即,
解得,
所以实数的取值范围是
故选:B
21.A
【详解】
因为函数的单调递增区间为,
所以根据复合函数单调性可知,的单调递增区间为
故选:A
22.B
【详解】
由得,
,所以的最小值为,
所以,.
故选:B.
23.B
【详解】
由题意分情况讨论:
①当时,
当时,单调递增,此时;
当时, 单调递减;
,单调递增,
故时,的最小值为,
故若有最小值,则;
② 当时,
当时,单调递减,此时;
当时,单调递增,此时,
故若有最小值,则,解得,
综上实数的取值范围是
故选:B
24.D
【详解】
当时,在单调递增,所以,解得:,所以此时,,
当时,在单调递减,所以,解得:
,所以此时,,
所以m的值为或,
故选:D
25.C
【详解】
某湖泊中的蓝藻每天以的增长率呈指数增长,经过30天以后,该湖泊的蓝藻数大约为原来的6倍,
设湖泊中原来蓝藻数量为,则,
经过60天后该湖泊的蓝藻数量为:
经过60天后该湖泊的蓝藻数大约为原来的36倍.
故选:C.
26.C
【详解】
解析:由题意知,当时,有.
即,得.
所以当时,有.
即,得.
所以.
故选:C
27.B
【详解】
由题意可得,解得.
故.
令,即,
两边同时取对数,故分钟
故选:B
28.B
【详解】
解:∵,
函数是减函数,,∴,∴.
又函数是R上的增函数,,∴,即,
综上可得,,
故选:B.
29.D
【详解】
,在定义域内都不是单调递增的,不满足题意,
在定义域上单调递减,不满足题意,
在定义域上单调递增,满足题意,.
故选:D
30.B
【详解】
由可得,
因为在上单调递增,
所以即,解得:,
所以,即函数的值域是,
故选:B.
31.C
解:满足对任意,都有成立,
在上是减函数,
因为
,解得,
的取值范围是.
故选:.
32.C
【详解】
解:,定义域为
,
为奇函数,故可排除,;
又在定义域上单调递增,在定义域上单调递减,
在上是增函数,符合题意,可排除;
故选:.
33.A
【详解】
由,可得,
因为由图像可知函数是减函数,所以,所以,
因为,
所以,所以,
故选:A
34.D
【详解】
由,且,排除AC;
∵,
当时,为单调递减函数,∴,与已知矛盾矛盾,故B错误;
当时,为单调递增函数,∴,符合题意.
故选:D.
35.A
【详解】
与是增函数,与是减函数,在第一象限内作直线,
该直线与四条曲线交点的纵坐标的大小对应各底数的大小,易知:选A.
故选:A
36.D
【详解】
函数y=a-x是把y=-ax中的x换成-x,把y换成-y,
所以两个函数的图像关于原点对称,
故选:D.
37.D
【详解】
当时,由,则,
即,解得或,
所以或,
又因,所以;
当时,,
由,即,即,
即,解得,
所以,
又因,所以,
综上所述:不等式的解集为.
故选:D.
38.B
【详解】
要使有意义,则,解得,所以函数的定义域为.
故选:B.
39.D
【详解】
令,则,
故原函数化为,
当时,可得最小值为.
故选:D.
40.D
【详解】
解:根据题意,是定义在,上的偶函数,则有,则,
同时,即,则有,必有,
则,其定义域为,,
则,设,若,则有,
在区间,上,且为减函数,
在区间,上为增函数,
则在,上为减函数,其最大值为,
故选:.
41.C
【详解】
,.∵.∴.
又∵,,∴.
∴有.
又因为镜片折射率越高,镜片越薄,故甲同学创作的镜片最厚,乙同学创作的镜片最薄.
故选:C.
42.C
【详解】
由题意知,当x=1时,y=3,故A(1,3),m+n=4,
故选:C.
43.A
【详解】
由,得.
当时,,
所以B,D错误;
当时,,所以C错误.
故选:.
44.ABC
【详解】
A.当时,,此时为奇函数,故选项A正确;
B.为偶函数,在区间上为减函数,图象过点,且以x轴为渐近线.
若函数的图象经过原点,且渐近线为时,,,选项B正确;
C.因为偶函数,在区间上为减函数,
故若函数在区间上单调递减,则,选项C正确:
D.当时,,,若恒成立,得,即,而,此时,,
当时,,得,若恒成立,得,
当时,,得,
若恒成立,得,即,而,因此得,
选项D不正确,
故选:ABC.
45.ACD
【详解】
的定义域为关于原点对称,
,所以是奇函数,图象关于原点对称,
故选项A正确,选项B不正确;
,因为,所以,所以,
,所以,可得的值域为,故选项C正确;
设任意的,
则,
因为,,,所以,
即,所以,故选项D正确;
故选:ACD
46.ABD
【详解】
A:由在定义域上的值域为,显然不符合,;
B:在定义域上单调递增,但在定义域上有,即为奇函数,不符合题设函数性质;
C:在定义域上是偶函数,在上单调递增,且,符合题设函数的性质;
D:由幂函数的性质知:在上单调递减,不合题设函数性质;
故选:ABD.
47.ACD
【详解】
对于A,,则,
则为奇函数,故图象关于原点对称,故A正确.
对于B,计算,,故的图象不关于y轴对称,故B错误.
对于C,,,
故,易知:,故的值域为,故C正确.
对于D,,
因为在上为增函数,为上的减函数,
由复合函数的单调性的判断法则可得在上单调递减,
故,且,恒成立,故D正确.
故选:ACD.
48.ABD
【详解】
解:因为函数(且)在上为单调函数,
所以或,解得或,所以满足条件的有ABD;
故选:ABD
49.ACD
【详解】
函数,定义域为R,
又指数函数是单调递增的,可知是单调递减的,取值为,
故是单调递增的,值域为,故A正确;
当时,,当时,,
故的值域是,D正确;
又,故是奇函数,即C正确;
因为,故,,故,即,故不可能是偶函数,B错误.
故选:ACD.
50.
由指数函数的性质知:,
∴.
故答案为:
51.
由题意,的值域为:
要使得:的值域为
必为减函数,因此
可作出函数图象如图,由图象可知解之得.
故答案为:
52.
【详解】
原不等式可变形为,因为指数函数为增函数,
则有,
即对一切实数恒成立.
①当时,,满足题意;
②当时,若二次函数大于0恒成立,则需且,
即且,解得.
综上,实数的取值范围是.
故答案为:
53.36倍
【详解】
某湖泊中的蓝藻每天以的增长率呈指数增长,经过30天以后,该湖泊的蓝藻数大约为原来的6倍,
设湖泊中原来蓝藻数量为,则,
经过60天后该湖泊的蓝藻数量为:
经过60天后该湖泊的蓝藻数大约为原来的36倍.
故答案为:36倍
54.(1,+∞)
【详解】
设F(x)=f(x)-2,则F(x)=,易知F(x)是奇函数,F(x)===1-在R上是增函数,
由f(a)+f(a-2)>4得F(a)+F(a-2)>0,
于是可得F(a)>F(2-a),即a>2-a,解得a>1.
答案:(1,+∞)
55.
解:(1)函数的简图如下:
(2)由图可知,函数的增区间为,减区间为;
(3)由,及函数的单调性可知,
若则实数的值为或.
56.
解:(1)由函数是R上的奇函数知,
即,解得.
(2)由(1)知.
任取,则
因为,所以,所以,
又因为,故,
所以,即
所以在上为减函数.
(3)不等式可化为
因为是奇函数,故
所以不等式可化为
由(2)知在上为减函数,故即
即对于任意,不等式恒成立.
设易知
因此
所以实数的取值范围是.
57.【详解】
(1),即,而,则,解得,显然在上单调递减,
又,于是得在上是奇函数,
从而有等价于,
由原不等式恒成立可得,即恒成立,亦即,解得:,
所以实数的取值范围是:;
(2),即,而,解得:,
所以,
令,显然在上单调递增,则,
,对称轴为,
当时,,解得或(舍),则,
当时,,解得:不符合题意,
综上得,
所以实数m的值为2.
58.(1);(2).
(1)是奇函数,是偶函数,
由,①
得,②
①②得,①②得.
又,,,
.
(2)由(1)可得,故,
由基本不等式可得,
令,则且,设,
当即时,;
当即时,,
故.
59.(1);(2)①;②.
【详解】
(1)
所以;
(2)①,
令,所以,
令或.
当时,;
当时,;
当时,.
所以.
②函数的图象如图所示,
从函数的图象和解析式可以看出函数单调递减,
因为对于恒成立,
所以,
所以.
所以.
60.(1);(2);(3).
解:(1)因为,
所以
设,,
原不等式可化为,
整理可得,解得,
即,解得,
所以不等式的解集为.
(2)设,由可得,
则,
令,
由二次函数的知识可得,当时,,当时,,
故函数的值域为,
函数有零点等价于方程有解,等价于在的值域内,
故的取值范围为
(3)由题意得解得
即,对任意恒成立,
又时,令,则,
因为在上单调递增,
当时,有最大值,
所以
试卷第1页,共3页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
