人教A版2019必修第一册5.5.2 简单的三角恒等变换 学案(Word版含答案)
文档属性
| 名称 | 人教A版2019必修第一册5.5.2 简单的三角恒等变换 学案(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 15:40:42 | ||
图片预览



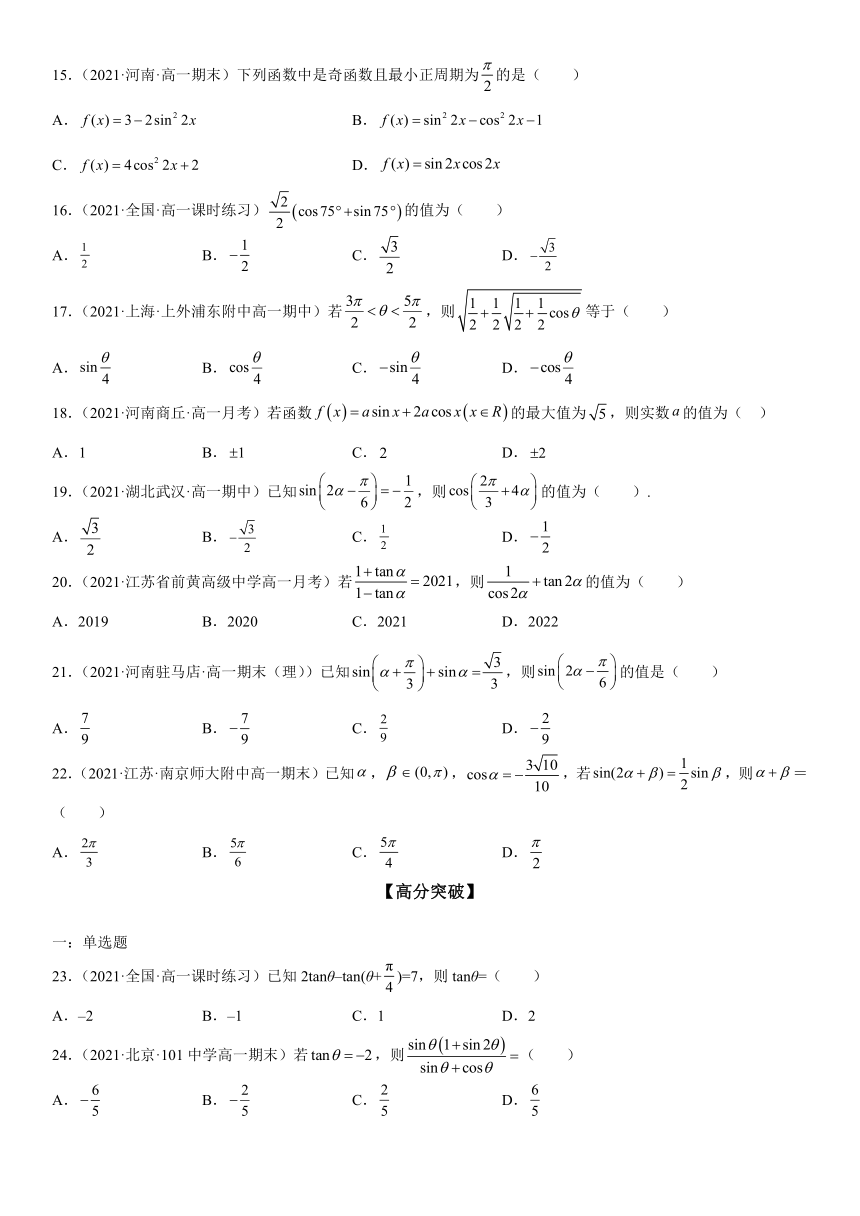

文档简介
5.5 三角恒等变换
5.5.2 简单的三角恒等变换
【考点梳理】
考点一 半角公式
sin =±,cos =±,tan =±==.
考点二 辅助角公式
辅助角公式:
asin x+bcos x=sin(x+θ).
【题型归纳】
题型一:降幂公式的化简求值问题
1.(2021·全国·高一课时练习)化简:
(1);(2);(3);
(4);(5);(6).
2.(2021·全国·高一课时练习)利用倍角公式求下列各式的值:
(1);(2);(3);(4);
(5);(6).
3.(2020·山西·怀仁市第一中学校云东校区高一期中(文))求值:
(1)若,求的值.(2)求的值.
题型二:辅助角公式的应用
4.(2021·河北迁安·高一期末)已知函数.
(1)求函数的最小正周期;
(2)求函数的单调减区间;
(3)当时,画出函数的图象.
5.(2021·甘肃·庆阳第六中学高一期末)已知函数.
(1)求函数的最小正周期;
(2)当时,求函数的值域.
6.(2021·上海·高一课时练习)化简并求值.
(1);
(2);
(3);
(4).
题型三:三角恒等式变换中的(给角求值、给值求值、给值求角)问题
7.(2021·全国·高一课时练习)求下列函数的最大值和最小值:
(1);(2);
(3);(4).
8.(2021·四川·成都外国语学校高一月考)已知函数,函数的最小正周期是( )
A. B. C. D.
9.(2021·全国·高一课时练习)(1)求的值;
(2)已知均为锐角,且,求的值.
题型四:三角恒等式变换中证明、化简问题
10.(2021·全国·高一课时练习)证明:
(1);(2);
(3);(4);
(5);(6).
11.(2021·全国·高一课时练习)求下列各式的值:
(1)已知,求的值;
(2)求的值;
12.(2021·河南驻马店·高一期末(理))化简,求值:
(Ⅰ)已知,求;
(Ⅱ)
13.(2021·四川·仁寿一中高一开学考试)已知,.
(1)求;
(2)已知,.求.
【双基达标】
一、单选题
14.(2021·全国·高一课时练习)若,是第三象限的角,则=( )
A.2 B. C.﹣2 D.
15.(2021·河南·高一期末)下列函数中是奇函数且最小正周期为的是( )
A. B.
C. D.
16.(2021·全国·高一课时练习)的值为( )
A. B. C. D.
17.(2021·上海·上外浦东附中高一期中)若,则等于( )
A. B. C. D.
18.(2021·河南商丘·高一月考)若函数的最大值为,则实数的值为( )
A. B. C. D.
19.(2021·湖北武汉·高一期中)已知,则的值为( ).
A. B. C. D.
20.(2021·江苏省前黄高级中学高一月考)若,则的值为( )
A.2019 B.2020 C.2021 D.2022
21.(2021·河南驻马店·高一期末(理))已知,则的值是( )
A. B. C. D.
22.(2021·江苏·南京师大附中高一期末)已知,,,若,则=( )
A. B. C. D.
【高分突破】
一:单选题
23.(2021·全国·高一课时练习)已知2tanθ–tan(θ+)=7,则tanθ=( )
A.–2 B.–1 C.1 D.2
24.(2021·北京·101中学高一期末)若,则( )
A. B. C. D.
25.(2021·上海·高一期中)已知,,且,,则( )
A. B. C. D.
26.(2021·福建·莆田锦江中学高一期末)若,,,则( )
A. B. C. D.
27.(2021·山西·怀仁市第一中学校云东校区高一月考(理))若,,,,则( )
A. B. C. D.
28.(2021·江苏·扬州大学附属中学高一月考)已知,则的值为( )
A. B. C. D.
29.(2021·全国·高一专题练习)函数的最大值和最小值分别为( )
A. B. C.,0 D.
30.(2021·浙江·高一期末)已知则( )
A. B. C. D.
31.(2018·四川资阳·高一期末)已知,,则的值为
A. B. C. D.
32.(2021·全国·高一课时练习)德国著名的天文学家开普勒说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.如果把勾股定理比作黄金矿的话,那么可以把黄金分割比作钻石矿.”黄金三角形有两种,其中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形,它是一个顶角为的等腰三角形(另一种是顶角为的等腰三角形).例如,五角星由五个黄金三角形与一个正五边形组成,如图所示,在其中一个黄金中,.根据这些信息,可得( )
A. B. C. D.
二、多选题
33.(2021·海南·琼中中学高一期中)已知,,则( )
A. B.
C. D.
34.(2020·全国·高一课时练习)设函数,则
A.是偶函数 B.在单调递减
C.最大值为2 D.其图像关于直线对称
35.(2021·江苏·常熟市中学高一月考)已知,,,,则( )
A. B.
C. D.
36.(2021·山东枣庄·高一期末)下列化简正确的是( )
A. B.
C. D.
37.(2021·江苏·仪征市第二中学高一月考)下列说法正确的是( )
A.
B.
C.
D.
38.(2021·江苏·南京市秦淮中学高一月考)下列等式中恒成立的是( )
A. B.
C. D.
三、填空题
39.(2020·全国·高一课时练习)函数的最大值为__________.
40.(2021·河北·藁城新冀明中学高一月考)已知 =,则的值是____.
41.(2020·四川·棠湖中学高一月考)__________.
42.(2021·广东·金山中学高一期中)已知,则______.
43.(2021·全国·高一课时练习)已知,则的值为______.
44.(2020·福建省南平市高级中学高一期中)若都是锐角,,,则 .
45.(2021·安徽舒城·高一期末)若,则__________.
46.(2021·山东滨州·高一期末)函数在区间上的最大值为____________.
47.(2019·河南驻马店·高一期末(文))已知当时,函数(且)取得最大值,则时,的值为__________.
四、解答题
48.(2021·全国·高一课时练习)化简:
(1);
(2);
(3).
49.(2021·全国·高一课时练习)证明:
(1);
(2).
50.(2021·全国·高一课时练习)化简:
(1);
(2).
51.(2021·全国·高一课时练习)解答:
(1)化简:;
(2)求值:;
(3)求函数的最大值.
52.(2021·北京·大峪中学高一期中)已知,且.
(1)求的值;
(2)求的值.
53.(2021·上海市民办西南高级中学高一月考)(1)已知,,求的值;
(2)已知,,求.
【答案详解】
.1.
(1)
(2)
(3)
(4)
(5)
(6)
因为,所以,所以,
因此原式.
2.
(1)
(2)
(3)
(4)
(5)
(6)
3.
(1)
由,
等式左边分子、分母同除得,,解得,
则.
(2)
.
4.(1);(2);(2)详见解析.
【详解】
(1),
,
,
所以函数的周期为;
(2)令,
解得,
所以函数的单调减区间是;
(3)由列表如下:
0
x
y 0 -2 0 2 0
则函数的图象如下:
.
5.(1);(2).
【详解】
(1)由,
所以函数的最小正周期为.
(2)时,,
,
∴的值域为.
6.(1);(2);(3);(4)32.
【详解】
(1)原式
.
(2)原式
.
(3)原式
.
(4)原式
.
7.
(1)
,最大值为1,最小值为;
(2)
,最大值为,最小值为;
(3)
,最大值为2,最小值为;
(4)
,最大值为2,最小值为.
8.B
【详解】
所以的最小正周期为,
故选:B
9.(1);(2).
【详解】
(1)原式
(2)因为均为锐角,,
所以,,由
根据函数在上为增函数,所以
所以.
又均为锐角,则,所以
10.
(1)
左边==右边,原式成立.
(2)
左边 =右边,原式成立.
(3)
左边 =右边,原式成立.
(4)
左边 =右边,原式成立.
(5)
左边 =右边,原式成立.
(6)
左边
=右边,原式成立.
11.(1); ;(2) .
【详解】
(1),
.
(2)原式.
12.(Ⅰ);(Ⅱ)16.
解:(Ⅰ)由,所以,解得,
所以
(Ⅱ)
13.(1);(2).
解:(1),,
(2)
,
14.C
【详解】
由且是第三象限的角,可得,
又由,即.
故选:C.
15.D
【详解】
由选项A得,
所以该函数为偶函数,且最小正周期为,选项A错误;
对于选项B,,该函数为偶函数,且最小正周期为,选项B错误;
对于选项C,.该函数为偶函数.且最小正周期为,选项C错误;
对于选项D,,该函数是奇函数且最小正周期为,D选项正确.
故选:D
16.C
【详解】
故选:C.
17.A
解:,,,
所以,,,
,
.
故选:A.
18.B
【详解】
依题意, ,
设锐角满足,则.
当时,函数的最大值为因此.
当时,函数的最大值为解得.
综上,实数的值为.
故选:B.
19.D
【详解】
,
,
,
,
故选:D
20.C
【详解】
.
故选:C
21.B
【详解】
,即,
,,
则
,
故选:B.
22.C
解:因为
若,则,即,
,则,所以,,即
又,所以.
故选:C
23.D
【详解】
,,
令,则,整理得,解得,即.
故选:D.
【点睛】
本题主要考查了利用两角和的正切公式化简求值,属于中档题.
24.C
【详解】
将式子进行齐次化处理得:
.
故选:C.
25.A
【详解】
且,,.
又,,.
当时,
,
,,不合题意,舍去;
当,同理可求得,符合题意.
综上所述:.
故选:.
26.C
【详解】
由题意,故
故
又,
故
,
则
故选:C
27.C
【详解】
,
因为,,
所以,,
因为,,
所以,,
则.
故选:C
28.D
【详解】
因为
,
所以,
故选:D
29.D
【详解】
设,则,则
,
由,得,所以,
所以当,即时,;当,即时,.
故选:D.
30.B
【详解】
由得,
故.
所以.
故选:B
31.A
详解:∵,,
∴,
∴,
.
∴.
故选A.
32.C
因为是顶角为的等腰三角形,所以,,
则,,
而,所以,.
故选:C.
33.AC
【详解】
∵,,且
解得:
∴,故A正确;
,故B错误;
,故C正确;
∵,∴.
∵,∴,故D错误.
故选:AC
34.ABD
【详解】
.
选项A:,它是偶函数,本说法正确;
选项B:,所以,因此是单调递减,本说法正确;
选项C:的最大值为,本说法不正确;
选项D:当时,,因此当时,函数有最小值,因此函数图象关于对称,本说法正确.
故选:ABD
35.BC
【详解】
①因为,所以,
又,故有,,
解出,故A错误;
②,
由①知:,所以,
所以,故B正确;
③由①知:,而,所以,
又,所以,
解得,
所以
又因为,,
所以,有,故C正确;
④由,
由③知,,
两式联立得:,故D错误.
故选:BC
36.ABD
【详解】
对于选项A:,
故选项A正确;
对于选项B:,故选项B正确;
对于选项C:
,故选项C不正确;
对于选项D:
,
故选项D正确;
故选:ABD.
37.AB
【详解】
对于A,
,故A正确;
对于B,由两角和的正弦公式,
,故B正确.
对于C,,故C错误.
对于D,,故D错误.
故选:AB
38.ACD
【详解】
选项A. 由,则成立,故A 正确.
选项B. 由
当 时,,
则此时,所以B不正确.
选项C.
,故C正确.
选项D.
所以成立,故D正确
故选:ACD
39.
解:函数f(x)=2cosx+sinx(cosxsinx)sin(x+θ),其中tanθ=2,
可知函数的最大值为:.
故答案为.
40.
【详解】
故答案为:
【点睛】
本题考查两角和正弦公式、二倍角正弦公式,考查基本分析求解能力,属基础题.
41.1
【解析】
,
.
42.1
【详解】
因为,
所以.
故答案为:.
43.
【详解】
因为,,
所以,,
所以.
故答案为:.
44.
【解析】
①
因为,所以 ,又因为,所以 , ,代入①得,故填:
45.
【详解】
由可以得到,
所以,设,则
则,
所以.
故答案为.
46.
,
因为,所以,
所以,
所以,
可得,
所以函数在区间上的最大值为,
故答案为:.
47.3
【详解】
,其中,
当时,函数取得最大值,则,,
所以,,
解得,故答案为.
48.
(1)
(2)
(3)
49.
(1)
证明:左边
右边,
所以;
(2)
证明:左边
右边,
所以.
50.
(1)
原式=
===1
故答案:1
(2)
原式====1
故答案:1
51.
解:原式.
(2)
解:原式
.
(3)
解:,故.
52.(1);(2).
【详解】
(1)因为,,
所以.
所以.
(2)因为,,
所以.
所以.
53.(1);(2).
【详解】
(1)因,,则,,
所以;
(2)因,则,由得,解得,(舍去),
所以,.
试卷第1页,共3页
5.5.2 简单的三角恒等变换
【考点梳理】
考点一 半角公式
sin =±,cos =±,tan =±==.
考点二 辅助角公式
辅助角公式:
asin x+bcos x=sin(x+θ).
【题型归纳】
题型一:降幂公式的化简求值问题
1.(2021·全国·高一课时练习)化简:
(1);(2);(3);
(4);(5);(6).
2.(2021·全国·高一课时练习)利用倍角公式求下列各式的值:
(1);(2);(3);(4);
(5);(6).
3.(2020·山西·怀仁市第一中学校云东校区高一期中(文))求值:
(1)若,求的值.(2)求的值.
题型二:辅助角公式的应用
4.(2021·河北迁安·高一期末)已知函数.
(1)求函数的最小正周期;
(2)求函数的单调减区间;
(3)当时,画出函数的图象.
5.(2021·甘肃·庆阳第六中学高一期末)已知函数.
(1)求函数的最小正周期;
(2)当时,求函数的值域.
6.(2021·上海·高一课时练习)化简并求值.
(1);
(2);
(3);
(4).
题型三:三角恒等式变换中的(给角求值、给值求值、给值求角)问题
7.(2021·全国·高一课时练习)求下列函数的最大值和最小值:
(1);(2);
(3);(4).
8.(2021·四川·成都外国语学校高一月考)已知函数,函数的最小正周期是( )
A. B. C. D.
9.(2021·全国·高一课时练习)(1)求的值;
(2)已知均为锐角,且,求的值.
题型四:三角恒等式变换中证明、化简问题
10.(2021·全国·高一课时练习)证明:
(1);(2);
(3);(4);
(5);(6).
11.(2021·全国·高一课时练习)求下列各式的值:
(1)已知,求的值;
(2)求的值;
12.(2021·河南驻马店·高一期末(理))化简,求值:
(Ⅰ)已知,求;
(Ⅱ)
13.(2021·四川·仁寿一中高一开学考试)已知,.
(1)求;
(2)已知,.求.
【双基达标】
一、单选题
14.(2021·全国·高一课时练习)若,是第三象限的角,则=( )
A.2 B. C.﹣2 D.
15.(2021·河南·高一期末)下列函数中是奇函数且最小正周期为的是( )
A. B.
C. D.
16.(2021·全国·高一课时练习)的值为( )
A. B. C. D.
17.(2021·上海·上外浦东附中高一期中)若,则等于( )
A. B. C. D.
18.(2021·河南商丘·高一月考)若函数的最大值为,则实数的值为( )
A. B. C. D.
19.(2021·湖北武汉·高一期中)已知,则的值为( ).
A. B. C. D.
20.(2021·江苏省前黄高级中学高一月考)若,则的值为( )
A.2019 B.2020 C.2021 D.2022
21.(2021·河南驻马店·高一期末(理))已知,则的值是( )
A. B. C. D.
22.(2021·江苏·南京师大附中高一期末)已知,,,若,则=( )
A. B. C. D.
【高分突破】
一:单选题
23.(2021·全国·高一课时练习)已知2tanθ–tan(θ+)=7,则tanθ=( )
A.–2 B.–1 C.1 D.2
24.(2021·北京·101中学高一期末)若,则( )
A. B. C. D.
25.(2021·上海·高一期中)已知,,且,,则( )
A. B. C. D.
26.(2021·福建·莆田锦江中学高一期末)若,,,则( )
A. B. C. D.
27.(2021·山西·怀仁市第一中学校云东校区高一月考(理))若,,,,则( )
A. B. C. D.
28.(2021·江苏·扬州大学附属中学高一月考)已知,则的值为( )
A. B. C. D.
29.(2021·全国·高一专题练习)函数的最大值和最小值分别为( )
A. B. C.,0 D.
30.(2021·浙江·高一期末)已知则( )
A. B. C. D.
31.(2018·四川资阳·高一期末)已知,,则的值为
A. B. C. D.
32.(2021·全国·高一课时练习)德国著名的天文学家开普勒说过:“几何学里有两件宝,一个是勾股定理,另一个是黄金分割.如果把勾股定理比作黄金矿的话,那么可以把黄金分割比作钻石矿.”黄金三角形有两种,其中底与腰之比为黄金分割比的黄金三角形被认为是最美的三角形,它是一个顶角为的等腰三角形(另一种是顶角为的等腰三角形).例如,五角星由五个黄金三角形与一个正五边形组成,如图所示,在其中一个黄金中,.根据这些信息,可得( )
A. B. C. D.
二、多选题
33.(2021·海南·琼中中学高一期中)已知,,则( )
A. B.
C. D.
34.(2020·全国·高一课时练习)设函数,则
A.是偶函数 B.在单调递减
C.最大值为2 D.其图像关于直线对称
35.(2021·江苏·常熟市中学高一月考)已知,,,,则( )
A. B.
C. D.
36.(2021·山东枣庄·高一期末)下列化简正确的是( )
A. B.
C. D.
37.(2021·江苏·仪征市第二中学高一月考)下列说法正确的是( )
A.
B.
C.
D.
38.(2021·江苏·南京市秦淮中学高一月考)下列等式中恒成立的是( )
A. B.
C. D.
三、填空题
39.(2020·全国·高一课时练习)函数的最大值为__________.
40.(2021·河北·藁城新冀明中学高一月考)已知 =,则的值是____.
41.(2020·四川·棠湖中学高一月考)__________.
42.(2021·广东·金山中学高一期中)已知,则______.
43.(2021·全国·高一课时练习)已知,则的值为______.
44.(2020·福建省南平市高级中学高一期中)若都是锐角,,,则 .
45.(2021·安徽舒城·高一期末)若,则__________.
46.(2021·山东滨州·高一期末)函数在区间上的最大值为____________.
47.(2019·河南驻马店·高一期末(文))已知当时,函数(且)取得最大值,则时,的值为__________.
四、解答题
48.(2021·全国·高一课时练习)化简:
(1);
(2);
(3).
49.(2021·全国·高一课时练习)证明:
(1);
(2).
50.(2021·全国·高一课时练习)化简:
(1);
(2).
51.(2021·全国·高一课时练习)解答:
(1)化简:;
(2)求值:;
(3)求函数的最大值.
52.(2021·北京·大峪中学高一期中)已知,且.
(1)求的值;
(2)求的值.
53.(2021·上海市民办西南高级中学高一月考)(1)已知,,求的值;
(2)已知,,求.
【答案详解】
.1.
(1)
(2)
(3)
(4)
(5)
(6)
因为,所以,所以,
因此原式.
2.
(1)
(2)
(3)
(4)
(5)
(6)
3.
(1)
由,
等式左边分子、分母同除得,,解得,
则.
(2)
.
4.(1);(2);(2)详见解析.
【详解】
(1),
,
,
所以函数的周期为;
(2)令,
解得,
所以函数的单调减区间是;
(3)由列表如下:
0
x
y 0 -2 0 2 0
则函数的图象如下:
.
5.(1);(2).
【详解】
(1)由,
所以函数的最小正周期为.
(2)时,,
,
∴的值域为.
6.(1);(2);(3);(4)32.
【详解】
(1)原式
.
(2)原式
.
(3)原式
.
(4)原式
.
7.
(1)
,最大值为1,最小值为;
(2)
,最大值为,最小值为;
(3)
,最大值为2,最小值为;
(4)
,最大值为2,最小值为.
8.B
【详解】
所以的最小正周期为,
故选:B
9.(1);(2).
【详解】
(1)原式
(2)因为均为锐角,,
所以,,由
根据函数在上为增函数,所以
所以.
又均为锐角,则,所以
10.
(1)
左边==右边,原式成立.
(2)
左边 =右边,原式成立.
(3)
左边 =右边,原式成立.
(4)
左边 =右边,原式成立.
(5)
左边 =右边,原式成立.
(6)
左边
=右边,原式成立.
11.(1); ;(2) .
【详解】
(1),
.
(2)原式.
12.(Ⅰ);(Ⅱ)16.
解:(Ⅰ)由,所以,解得,
所以
(Ⅱ)
13.(1);(2).
解:(1),,
(2)
,
14.C
【详解】
由且是第三象限的角,可得,
又由,即.
故选:C.
15.D
【详解】
由选项A得,
所以该函数为偶函数,且最小正周期为,选项A错误;
对于选项B,,该函数为偶函数,且最小正周期为,选项B错误;
对于选项C,.该函数为偶函数.且最小正周期为,选项C错误;
对于选项D,,该函数是奇函数且最小正周期为,D选项正确.
故选:D
16.C
【详解】
故选:C.
17.A
解:,,,
所以,,,
,
.
故选:A.
18.B
【详解】
依题意, ,
设锐角满足,则.
当时,函数的最大值为因此.
当时,函数的最大值为解得.
综上,实数的值为.
故选:B.
19.D
【详解】
,
,
,
,
故选:D
20.C
【详解】
.
故选:C
21.B
【详解】
,即,
,,
则
,
故选:B.
22.C
解:因为
若,则,即,
,则,所以,,即
又,所以.
故选:C
23.D
【详解】
,,
令,则,整理得,解得,即.
故选:D.
【点睛】
本题主要考查了利用两角和的正切公式化简求值,属于中档题.
24.C
【详解】
将式子进行齐次化处理得:
.
故选:C.
25.A
【详解】
且,,.
又,,.
当时,
,
,,不合题意,舍去;
当,同理可求得,符合题意.
综上所述:.
故选:.
26.C
【详解】
由题意,故
故
又,
故
,
则
故选:C
27.C
【详解】
,
因为,,
所以,,
因为,,
所以,,
则.
故选:C
28.D
【详解】
因为
,
所以,
故选:D
29.D
【详解】
设,则,则
,
由,得,所以,
所以当,即时,;当,即时,.
故选:D.
30.B
【详解】
由得,
故.
所以.
故选:B
31.A
详解:∵,,
∴,
∴,
.
∴.
故选A.
32.C
因为是顶角为的等腰三角形,所以,,
则,,
而,所以,.
故选:C.
33.AC
【详解】
∵,,且
解得:
∴,故A正确;
,故B错误;
,故C正确;
∵,∴.
∵,∴,故D错误.
故选:AC
34.ABD
【详解】
.
选项A:,它是偶函数,本说法正确;
选项B:,所以,因此是单调递减,本说法正确;
选项C:的最大值为,本说法不正确;
选项D:当时,,因此当时,函数有最小值,因此函数图象关于对称,本说法正确.
故选:ABD
35.BC
【详解】
①因为,所以,
又,故有,,
解出,故A错误;
②,
由①知:,所以,
所以,故B正确;
③由①知:,而,所以,
又,所以,
解得,
所以
又因为,,
所以,有,故C正确;
④由,
由③知,,
两式联立得:,故D错误.
故选:BC
36.ABD
【详解】
对于选项A:,
故选项A正确;
对于选项B:,故选项B正确;
对于选项C:
,故选项C不正确;
对于选项D:
,
故选项D正确;
故选:ABD.
37.AB
【详解】
对于A,
,故A正确;
对于B,由两角和的正弦公式,
,故B正确.
对于C,,故C错误.
对于D,,故D错误.
故选:AB
38.ACD
【详解】
选项A. 由,则成立,故A 正确.
选项B. 由
当 时,,
则此时,所以B不正确.
选项C.
,故C正确.
选项D.
所以成立,故D正确
故选:ACD
39.
解:函数f(x)=2cosx+sinx(cosxsinx)sin(x+θ),其中tanθ=2,
可知函数的最大值为:.
故答案为.
40.
【详解】
故答案为:
【点睛】
本题考查两角和正弦公式、二倍角正弦公式,考查基本分析求解能力,属基础题.
41.1
【解析】
,
.
42.1
【详解】
因为,
所以.
故答案为:.
43.
【详解】
因为,,
所以,,
所以.
故答案为:.
44.
【解析】
①
因为,所以 ,又因为,所以 , ,代入①得,故填:
45.
【详解】
由可以得到,
所以,设,则
则,
所以.
故答案为.
46.
,
因为,所以,
所以,
所以,
可得,
所以函数在区间上的最大值为,
故答案为:.
47.3
【详解】
,其中,
当时,函数取得最大值,则,,
所以,,
解得,故答案为.
48.
(1)
(2)
(3)
49.
(1)
证明:左边
右边,
所以;
(2)
证明:左边
右边,
所以.
50.
(1)
原式=
===1
故答案:1
(2)
原式====1
故答案:1
51.
解:原式.
(2)
解:原式
.
(3)
解:,故.
52.(1);(2).
【详解】
(1)因为,,
所以.
所以.
(2)因为,,
所以.
所以.
53.(1);(2).
【详解】
(1)因,,则,,
所以;
(2)因,则,由得,解得,(舍去),
所以,.
试卷第1页,共3页
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
