11.2.1 第2课时 三角形的内角和应用 课件(共18张PPT)
文档属性
| 名称 | 11.2.1 第2课时 三角形的内角和应用 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 08:56:43 | ||
图片预览




文档简介
(共18张PPT)
11.2 与三角形有关的角
11.2.1 三角形的内角
精品同步教学课件
第2课时 三角形的内角和应用
北
.
A
D
北
.
C
B
.
东
E
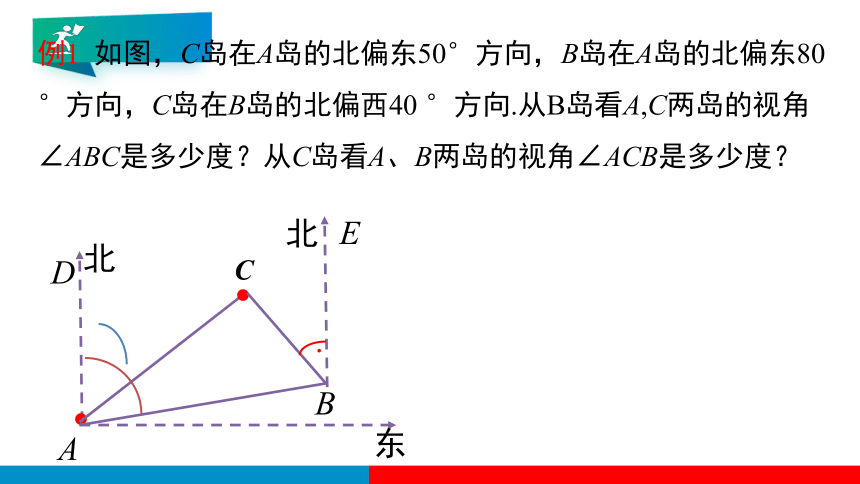
例1 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向.从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
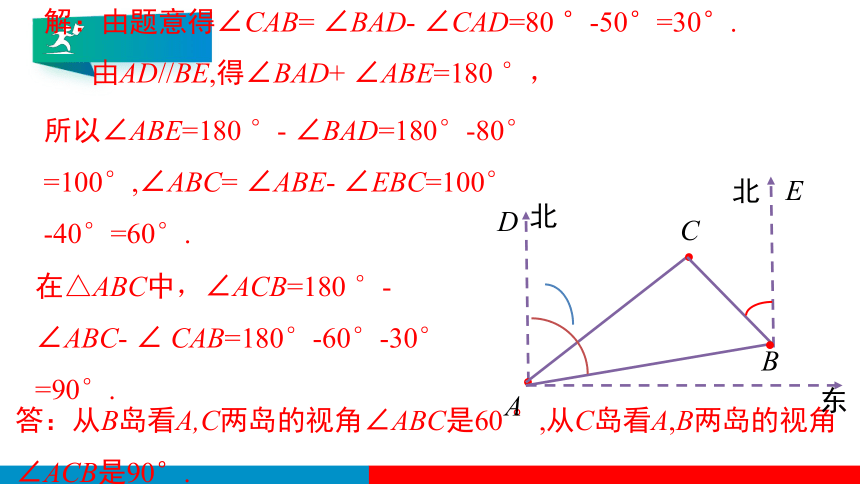
解:由题意得∠CAB= ∠BAD- ∠CAD=80 °-50°=30°.
由AD//BE,得∠BAD+ ∠ABE=180 °,
所以∠ABE=180 °- ∠BAD=180°-80°
=100°,∠ABC= ∠ABE- ∠EBC=100°
-40°=60°.
在△ABC中,∠ACB=180 °-∠ABC- ∠ CAB=180°-60°-30° =90°.
答:从B岛看A,C两岛的视角∠ABC是60 °,从C岛看A,B两岛的视角∠ACB是90°.
北
.
A
D
北
.
C
B
.
东
E
例2 如图,△ABC中,D在BC的延长线上,过D作DE⊥AB于E,交AC于F.已知∠A=30°,∠FCD=80°,求∠D.
解:∵DE⊥AB,∴∠FEA=90°.
∵在△AEF中,∠FEA=90°,∠A=30°,
∴∠AFE=180°-∠FEA-∠A=60°.
又∵∠CFD=∠AFE,
∴∠CFD=60°.
∴在△CDF中,
∠D=180°-∠CFD-∠FCD=40°.
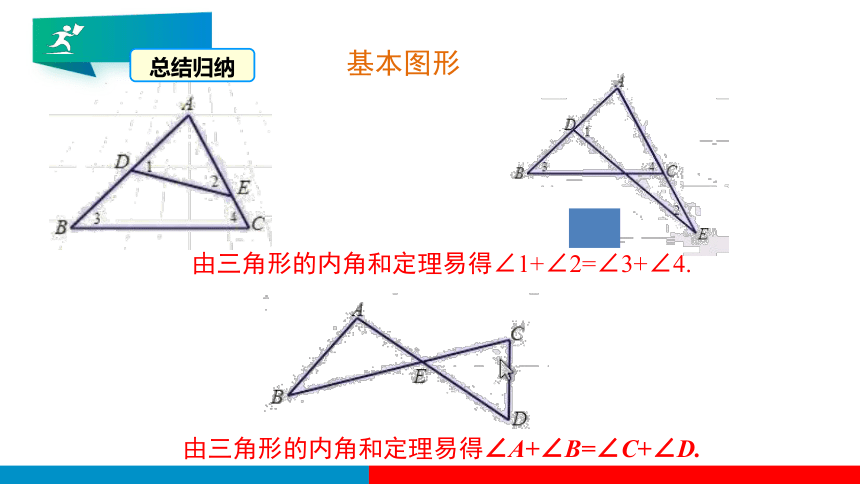
基本图形
由三角形的内角和定理易得∠A+∠B=∠C+∠D.
由三角形的内角和定理易得∠1+∠2=∠3+∠4.
总结归纳
例3 如图,在△ABC中,BP平分∠ABC,CP平分∠ACB.(1)若∠A=60°,求∠BPC的度数.
(1)解:∵在△ABC中,∠A=60°,
∴∠ABC+∠ACB=120°.
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB= (∠ABC+∠ACB)=60°.
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°-60°=120°.
拓展提升
(2)你能直接写出∠BPC与∠A 之间的数量关系吗?
(2)解:∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB= (∠ABC+∠ACB).
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°- (∠ABC+∠ACB)
=180°- (180°-∠A)=90°+ ∠A .
例2 如图,∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC 的度数.
∵ ∠A=42° ,∠ACE=18°,
∴ ∠BEC=∠A+∠ACE=42°+18°=60°.
∵ ∠ABD=28°,
∴ ∠BFC= ∠ABD+∠BEC
=28°+60°=88°.
解:
F
A
C
D
E
B
解:∵∠ADC是△ABD的外角,
练习:D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°,∠BAC=70°,求:
(1)∠B 的度数;(2)∠C的度数.
∵在△ABC中,∠B+∠BAC+∠C=180°,
∴∠C=180 -40 -70 =70°.
∴∠B+∠BAD=∠ADC==80°.
又∵∠B=∠BAD,
A
B
C
D
如图 ,试比较∠2 、∠1的大小;
如图 ,试比较∠3 、∠2、 ∠1的大小.
图
图
解:∵∠2=∠1+∠B,
∴∠2>∠1.
解:∵∠2=∠1+∠B,
∠3=∠2+∠D,
∴∠3>∠2>∠1.
三角形的外角大于与它不相邻的内角.
A
B
C
D
E
1
2
F
G
解:∵∠1是△FBE的外角,
∴∠1=∠B+ ∠E,
同理∠2=∠A+∠D.
在△CFG中,
∠C+∠1+∠2=180 ,
∴∠A+ ∠ B+∠C+ ∠ D+∠E
= 180 .
1.如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
1
2
3
B
A
C
P
N
M
D
E
F
2.如图,∠A+∠B+∠C+∠D+∠E+∠F
=________.
360°
【拓展2】如图,∠A=51°,∠B=20°,∠C=30°,求∠BDC的度数.
A
B
C
D
(
(
(
51 °
20 °
30 °
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
A
B
C
D
(
(
20 °
30 °
解法一:连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
E
)
)
1
2
)
3
)
4
你发现了什么结论?
A
B
C
D
(
(
(
51 °
20 °
30 °
E
)
1
解法二:延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC
=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
解法三:连接延长CD交AB于点F(解题过程同解法二).
)
2
F
解题的关键是正确的构造三角形,利用三角形外角的性质及转化的思想,把未知角与已知角联系起来求解.
总结
课堂小结
三角形的
内角和定理
证明
了解添加辅助线的方法及其目的
内容
三角形内角和等于180 °
https://www.21cnjy.com/help/help_extract.php
11.2 与三角形有关的角
11.2.1 三角形的内角
精品同步教学课件
第2课时 三角形的内角和应用
北
.
A
D
北
.
C
B
.
东
E
例1 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向.从B岛看A,C两岛的视角∠ABC是多少度?从C岛看A、B两岛的视角∠ACB是多少度?
解:由题意得∠CAB= ∠BAD- ∠CAD=80 °-50°=30°.
由AD//BE,得∠BAD+ ∠ABE=180 °,
所以∠ABE=180 °- ∠BAD=180°-80°
=100°,∠ABC= ∠ABE- ∠EBC=100°
-40°=60°.
在△ABC中,∠ACB=180 °-∠ABC- ∠ CAB=180°-60°-30° =90°.
答:从B岛看A,C两岛的视角∠ABC是60 °,从C岛看A,B两岛的视角∠ACB是90°.
北
.
A
D
北
.
C
B
.
东
E
例2 如图,△ABC中,D在BC的延长线上,过D作DE⊥AB于E,交AC于F.已知∠A=30°,∠FCD=80°,求∠D.
解:∵DE⊥AB,∴∠FEA=90°.
∵在△AEF中,∠FEA=90°,∠A=30°,
∴∠AFE=180°-∠FEA-∠A=60°.
又∵∠CFD=∠AFE,
∴∠CFD=60°.
∴在△CDF中,
∠D=180°-∠CFD-∠FCD=40°.
基本图形
由三角形的内角和定理易得∠A+∠B=∠C+∠D.
由三角形的内角和定理易得∠1+∠2=∠3+∠4.
总结归纳
例3 如图,在△ABC中,BP平分∠ABC,CP平分∠ACB.(1)若∠A=60°,求∠BPC的度数.
(1)解:∵在△ABC中,∠A=60°,
∴∠ABC+∠ACB=120°.
∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB= (∠ABC+∠ACB)=60°.
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°-60°=120°.
拓展提升
(2)你能直接写出∠BPC与∠A 之间的数量关系吗?
(2)解:∵BP平分∠ABC,CP平分∠ACB,
∴∠PBC+∠PCB= (∠ABC+∠ACB).
∵∠PBC+∠PCB+∠BPC=180°,
∴∠BPC=180°- (∠ABC+∠ACB)
=180°- (180°-∠A)=90°+ ∠A .
例2 如图,∠A=42°,∠ABD=28°,∠ACE=18°,求∠BFC 的度数.
∵ ∠A=42° ,∠ACE=18°,
∴ ∠BEC=∠A+∠ACE=42°+18°=60°.
∵ ∠ABD=28°,
∴ ∠BFC= ∠ABD+∠BEC
=28°+60°=88°.
解:
F
A
C
D
E
B
解:∵∠ADC是△ABD的外角,
练习:D是△ABC的BC边上一点,∠B=∠BAD, ∠ADC=80°,∠BAC=70°,求:
(1)∠B 的度数;(2)∠C的度数.
∵在△ABC中,∠B+∠BAC+∠C=180°,
∴∠C=180 -40 -70 =70°.
∴∠B+∠BAD=∠ADC==80°.
又∵∠B=∠BAD,
A
B
C
D
如图 ,试比较∠2 、∠1的大小;
如图 ,试比较∠3 、∠2、 ∠1的大小.
图
图
解:∵∠2=∠1+∠B,
∴∠2>∠1.
解:∵∠2=∠1+∠B,
∠3=∠2+∠D,
∴∠3>∠2>∠1.
三角形的外角大于与它不相邻的内角.
A
B
C
D
E
1
2
F
G
解:∵∠1是△FBE的外角,
∴∠1=∠B+ ∠E,
同理∠2=∠A+∠D.
在△CFG中,
∠C+∠1+∠2=180 ,
∴∠A+ ∠ B+∠C+ ∠ D+∠E
= 180 .
1.如图,求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数.
1
2
3
B
A
C
P
N
M
D
E
F
2.如图,∠A+∠B+∠C+∠D+∠E+∠F
=________.
360°
【拓展2】如图,∠A=51°,∠B=20°,∠C=30°,求∠BDC的度数.
A
B
C
D
(
(
(
51 °
20 °
30 °
思路点拨:添加适当的辅助线将四边形问题转化为三角形问题.
A
B
C
D
(
(
20 °
30 °
解法一:连接AD并延长于点E.
在△ABD中,∠1+∠ABD=∠3,
在△ACD中,∠2+∠ACD=∠4.
因为∠BDC=∠3+∠4,∠BAC=∠1+∠2,
所以∠BDC=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
E
)
)
1
2
)
3
)
4
你发现了什么结论?
A
B
C
D
(
(
(
51 °
20 °
30 °
E
)
1
解法二:延长BD交AC于点E.
在△ABE中,∠1=∠ABE+∠BAE,
在△ECD中,∠BDC=∠1+∠ECD.
所以∠BDC
=∠BAC+∠ABD+∠ACD
=51° +20°+30°=101°.
解法三:连接延长CD交AB于点F(解题过程同解法二).
)
2
F
解题的关键是正确的构造三角形,利用三角形外角的性质及转化的思想,把未知角与已知角联系起来求解.
总结
课堂小结
三角形的
内角和定理
证明
了解添加辅助线的方法及其目的
内容
三角形内角和等于180 °
https://www.21cnjy.com/help/help_extract.php
