2022-2023学年新高一入学考试数学试题1(福建)(Word版含解析)
文档属性
| 名称 | 2022-2023学年新高一入学考试数学试题1(福建)(Word版含解析) | 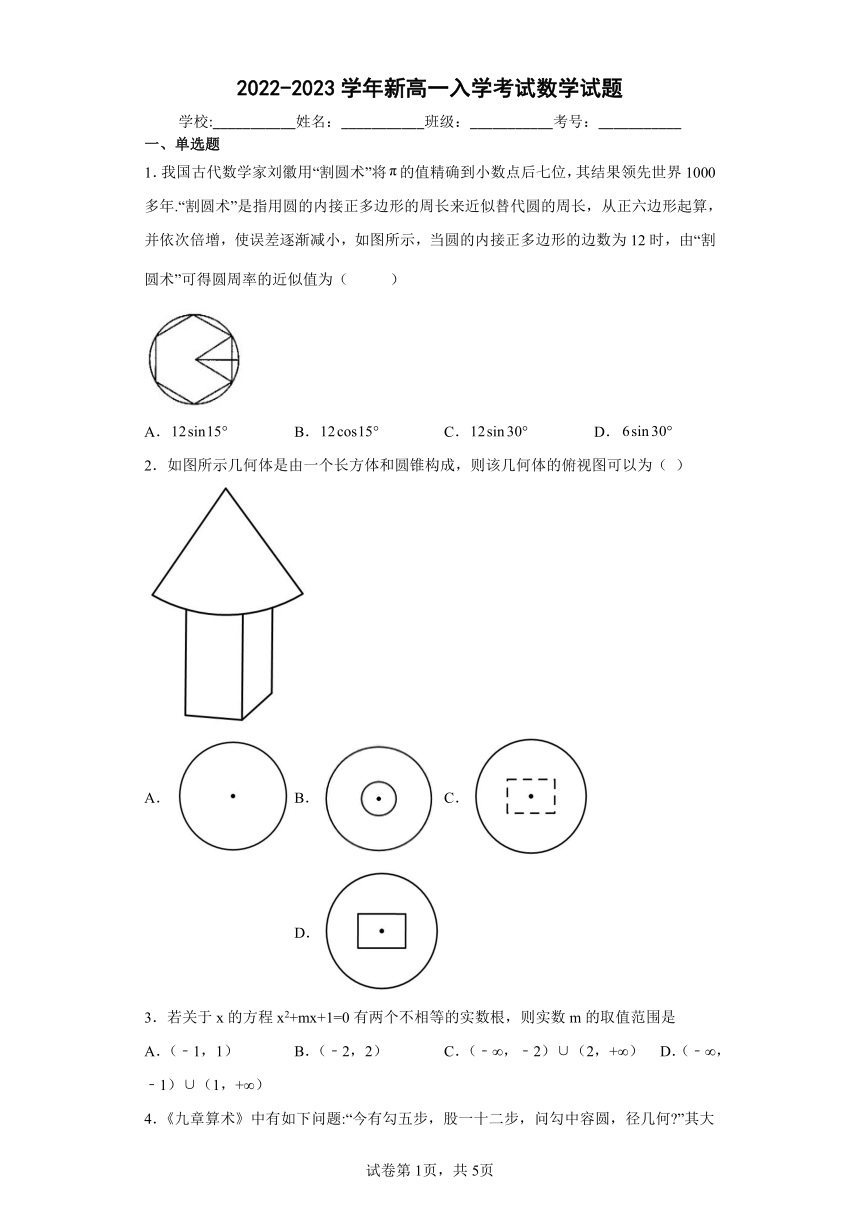 | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 16:29:33 | ||
图片预览





文档简介
2022-2023学年新高一入学考试数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.我国古代数学家刘徽用“割圆术”将的值精确到小数点后七位,其结果领先世界1000多年.“割圆术”是指用圆的内接正多边形的周长来近似替代圆的周长,从正六边形起算,并依次倍增,使误差逐渐减小,如图所示,当圆的内接正多边形的边数为12时,由“割圆术”可得圆周率的近似值为( )
A. B. C. D.
2.如图所示几何体是由一个长方体和圆锥构成,则该几何体的俯视图可以为( )
A. B. C. D.
3.若关于x的方程x2+mx+1=0有两个不相等的实数根,则实数m的取值范围是
A.(﹣1,1) B.(﹣2,2) C.(﹣∞,﹣2)∪(2,+∞) D.(﹣∞,﹣1)∪(1,+∞)
4.《九章算术》中有如下问题:“今有勾五步,股一十二步,问勾中容圆,径几何 ”其大意:“已知直角三角形两直角边长分别为5步和12步,问其内切圆的直径为多少步 ”则其内切圆的直径的步数为( )
A.1 B.2 C.3 D.4
5.如图,已知是半圆的直径,A是延长线上一点,切半圆于点D,于点C,于点F,若,则的半径为( )
A.3.5 B.4 C. D.3.75
6.一只盒子中有个红球,9个白球,个黑球,每个球除颜色外都有相同.已知至少摸出17个球时其中一定有5个红球,至少摸出17个球时其中一定有8个相同颜色的球,则代数式的值为( )
A.7 B.6 C.5 D.4
7.如图,正方形和正方形的边长分别为3和1,点,分别在边,上,为的中点,连接,则的长为( )
A. B.2 C. D.
8.某人从上一层到二层需跨10级台阶. 他一步可能跨1级台阶,称为一阶步,也可能跨2级台阶,称为二阶步,最多能跨3级台阶,称为三阶步. 从一层上到二层他总共跨了6步,而且任何相邻两步均不同阶. 则他从一层到二层可能的不同过程共有( )种.
A.6 B.8 C.10 D.12
二、填空题
9.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图所示的矩形由两个这样的图形拼成,若,则该矩形的面积为___________.
10.已知为等腰三角形,,边上的中线的长为7,则的面积为__________.
11.已知方程有两个负根,则k的取值集合为___________.
12.已知实数,满足方程,当时,的取值范围为________.
13.如图是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图中∠ACB=20°)时最为合适,已知货车车厢底部到地面的距离AB=1.5m,木板超出车厢部分AD=0.5m,则木板CD的长度为________.(参考数据:sin20°≈0.3420,cos20°≈0.9397,精确到0.1m).
14.如图,在等边中,分别为的中点,于点为的中点,连接,且,则的面积为__________.
15.如图,有一个边长不定的正方形,它的两个相对的顶点,分别在边长为1的正六边形一组平行的对边上,另外两个顶点,在正六边形内部(包括边界),则正方形边长的取值范围是___________.
16.若函数 在区间上为增函数,则的取值范围是______.
三、解答题
17.某班有甲、乙、丙三位学生在志愿者活动中表现优异,现从3人中选1人去参加全校表彰大会,有同学提议用如下方法:将4个编号为1,2,3,4的小球(形状、大小、质地都相同),放在一个不透明的袋中,按甲、乙、丙的顺序依次不放回地从袋中摸取一个小球,谁摸取的小球编号最大,谁就参加表彰大会.现用有序数组表示摸球的结果,例如表示甲、乙、丙摸取的小球编号分别为1,4,3.
(1)列出所有摸球的结果;
(2)求甲去参加表彰大会的概率,并判断该同学提议的方法是否公平.
18.已知关于的方程有两个实数根.
(1)求实数的取值范围;
(2)若满足,求实数的值.
19.如图,已知是的直径,弦与直径相交于点.点在外,作直线,且.
(1)求证:直线是的切线.
(2)若,,,求的长.
20.如图,在矩形中,是边上的一个动点,将四边形沿直线折叠,得到四边形,连接.
(1)若直线交于点,求证:;
(2)当时,求证:是等腰三角形;
(3)在点的运动过程中,求面积的最小值.
21.我国所需的高端芯片很大程度依赖于国外进口,“缺芯之痛”关乎产业安全、国家经济安全.如今,我国科技企业正在芯片自主研发之路中不断崛起.根据市场调查某手机品牌公司生产某款手机的年固定成本为40万美元,每生产1万部还需另投入16万美元.设该公司一年内共生产该款手机万部并全部销售完,每万部的销售收入为万美元,且当该公司一年内共生产该款手机2万部并全部销售完时,年利润为704万美元.
(1)写出年利润(万美元)关于年产量(万部)的函数解析式:
(2)当年产量为多少万部时,公司在该款手机的生产中所获得的利润最大 并求出最大利润.
22.已知二次函数的图象过点,且函数对称轴方程为.
(Ⅰ)求函数的解析式;
(Ⅱ)设函数,求在区间上的最小值;
(Ⅲ)探究:函数的图象上是否存在这样的点,使它的横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
设圆的半径为,圆的内接12边形的边长为,将圆的周长近似等于12边形的周长即可求解.
【详解】
设圆的半径为,则圆的内接12边形的边长为,
周长为,
由,得.
故选:A.
【点睛】
本题考查了圆的面积公式,考查了基本运算能力,属于基础题.
2.C
【解析】
【详解】
解:根据俯视图的定义,可知这个几何体的内部是一个柱体,上面是个圆锥,因此俯视图为选C.被挡住的部分用虚线表示.
3.C
【解析】
【详解】
试题分析:利用题中条件:“关于x的方程x2+mx+1=0有两个不相等的实数根”由韦达定理的出m的关系式,解不等式即可.
解:∵关于x的方程x2+mx+1=0有两个不相等的实数根,
∴△>0,
即:m2﹣4>0,
解得:m∈(﹣∞,﹣2)∪(2,+∞).
故选C.
点评:本题考查一元二次方程的根的判别式与根的关系,属于基本运算的考查.
4.D
【解析】
【分析】
求出三角形的斜边,根据三角形面积自等,即可求出内切圆半径,进而可得结果.
【详解】
设内切圆半径为R,三角形斜边为 ,
所以,直径为4
故选:D
5.D
【解析】
根据图形,连接OD,作于点H,由切半圆于点D,得到,又,则,易证,得到,设,然后在中,利用勾股定理求解.
【详解】
如图所示:
连接OD,作于点H,
因为切半圆于点D,
所以,又,
所以,
所以,
又,
所以,
所以,
设,则,
在中,由勾股定理得,
解得,
故选:D
【点睛】
本题主要考查圆的切线的性质,切割线定理,勾股定理等面积法以及平行线段成比例定理,还考查了数形结合的思想方法,属于中档题.
6.D
【解析】
【分析】
根据“至少摸出17个球时其中一定有5个红球得到方程,求得;根据“至少摸出17个球时一定有8个相同色的球”,最坏的情况,这17个球中一定包含3个黑球,这样其余的14个球只有红球和白球.为了保证这14个球中一定有8个颜色相同的球,于是得到,(8为白球数,若,则会出现,不能保证8个同色),即可得到结论.
【详解】
“至少摸出17个球时其中一定有5个红球”:“一定”包含最坏的情况,即摸完所有的白球和黑球才摸到红球,
,
;
“至少摸出17个球时一定有8个相同颜色的球”:最坏的情况:这17个球中一定包含3个黑球.
这样其余的14个球只有红球和白球.
为了保证这14个球中一定有8个颜色相同的球,
,(8为白球数,若,则会出现,不能保证8个同色),
.
故选:D.
7.C
【解析】
【分析】
延长交于点,作于点,则是的中位线,求得的长和的长,在中利用勾股定理求解.
【详解】
延长交于点,作于点.
则.
是的中点,
是的中位线,
.
直角中,,
是等腰直角三角形,
即,
同理中,.
.
在中,.
故选:C.
8.C
【解析】
【详解】
按题意要求,不难验证这6步中不可能没有三阶步,也不可能有多于1个的三阶步. 因此,只能是1个三阶步,2个二阶步,3个一阶步.
为形象起见,以白、黑、红三种颜色的球来记录从一层到二层跨越10级台阶的过程:
白球表示一阶步,黑球表示二阶步,红球表示三阶步. 每一过程可表为3个白球、2个黑球、1个红球的一种同色球不相邻的排列.
下面分三种情形讨论.
(1)第1、第6球均为白球,则两黑球必分别位于中间白球的两侧. 此时,共有4个黑白球之间的空位放置红球. 所以,此种情况共有4种可能的不同排列.
(2)第1球不是白球.
(i)第1球为红球,则余下5球只有一种可能的排列;
(ii)若第1球为黑球,则余下5球因红、黑球的位置不同有两种不同的排列,此种情形共有3种不同排列.
(3)第6球不是白球,同(2),共有3种不同排列.
总之,按题意要求从一层到二层共有种可能的不同过程.
9.12
【解析】
设小正方形的边长为,在中由勾股定理得,则可求出面积.
【详解】
设小正方形的边长为,
,,
在中,,
即,即,
则该矩形的面积为.
故答案为:12.
10.
【解析】
【分析】
先设等腰三角形的腰长为,进而可得底边的长,再由余弦定理列出方程,即可求出,从而可得结果.
【详解】
设等腰三角形的腰长为,因为,所以,
由余弦定理可得:,
,
因为与互补,所以,即,
解得,
所以,所以
故答案为
【点睛】
本题主要考查解三角形的问,常用余弦定理和正弦定理来处理,属于基础题型.
11.
【解析】
【分析】
根据判别式和韦达定理列式可求出结果.
【详解】
设方程的两个负根为,
所以,解得,
故答案为:
12.
【解析】
可知表示直线上的点与点连线的斜率,即可求出.
【详解】
实数,满足方程,当时,
表示直线上的点与点连线的斜率,
设、为直线上的两个点,且,
的斜率为,的斜率为 ,
故的范围为,
故答案为:.
13.
【解析】
【分析】
根据的正弦函数和的长度求的长,再加上即可.
【详解】
解:由题意可知:.
在中,,
,
.
故答案为:.
14.
【解析】
【分析】
根据题意设正三角形边长为,连接,则,化简求得,根据勾股定理列方程,可求,即可求解三角形面积.
【详解】
连接
设
则
且
且
在中
可得方程
解得
故
故答案为:
【点睛】
本题考查正三角形性质,平行关系和垂直关系,基础题型.
15.
【解析】
【分析】
当正方形的顶点 在正六边形的边上时,正方形的边长的值最大,解直角三角形得到,当正方形的对角线在正六边形一组平行的对边的中点上时,正方形边长的值最小,是正方形的对角线,解直角三角形即可得到结论.
【详解】
①当正方形的对角线在正六边形一组平行的对边的中点上时,
正方形边长的值最小,是正方形的对角线,
,
,
②当正方形的四个顶点都在正六边形的边上时,正方形边长的值最大,是正方形的对角线,
建立下图直角坐标系,设时,正方形的边长最大,
,
,
设直线的解析式为,,,
,
,
直线的解析式为,
将代入得,
此时,取最大值,
,
正方形边长的取值范围是:,
故答案为:.
16.
【解析】
【详解】
设 .
由题设知,当 时,在区间上为减函数,即 ,所以a≥16,矛盾.
当 时,在区间上为增函数,即 .
因此,的取值范围为.
故答案为
17.(1)答案见解析(2),公平
【解析】
(1)一一列举出所有的摸球结果(基本事件)即可,
(2)找到甲摸取的小球编号最大的结果(基本事件),根据概率公式计算即可,并作出判断.
【详解】
(1)基本事件为(1,2,3),(1,2,4),(1,3,2),(1,3,4),(1,4,2),(1,4,3),(2,1,3),(2,1,4),(2,3,1),(2,3,4),(2,4,1),(2,4,3),(3,1,2),(3,1,4),(3,2,1),(3,2,4),(3,4,1),(3,4,2),(4,1,2),(4,1,3),(4,2,1),(4,2,3),(4,3,1),(4,3,2),基本事件的总数为24.
(2) 甲去参加表彰大会包含的基本事件为(3,1,2),(3,2,1),(4,1,2),(4,1,3),(4,2,1),(4,2,3),(4,3,1),(4,3,2),共8个基本事件,
所以甲去参加表彰大会的概率,
甲乙丙三名同学获胜的概率与其摸取的次序是无关,该方法是公平的.
18.(1)
(2)
【解析】
【分析】
(1)利用判别式的意义得到,然后解不等式即可;
(2)利用根与系数的关系得到,,利用得到,然后解方程后利用的范围确定的值.
(1)关于的方程有两个实数根,,解得.
(2)关于的方程有两个实数根,,,,,整理得,解得,,,的值为.
19.(1)证明见解析
(2)
【解析】
【分析】
(1)根据切线的判定即可得直线是的切线.
(2)根据直径所对圆周角是直角可得,根据,,即可求的长.
(1)证明:连接,是的直径,,即,,,,即,直线是的切线;
(2)过点作边的垂线交于点.,,,,,,在中,.
20.(1)证明见解析
(2)证明见解析
(3)4
【解析】
【分析】
(1)根据题意证明即可证明结论;
(2)分别过点作于点于点,进而根据几何关系证明是垂直平分线即可证明结论;
(3)作点关于的对称点,点落在以点B为圆心,以AB为半径的弧AM上.设弧交于点,过点作于,进而得当点落在点处时,的面积最小,再根据即可得答案.
(1)证明:∵四边形是矩形,
∴.
∴.
根据对称可得,
∴.
∴.
(2)
证明:如图2,分别过点作于点于点,
∵四边形是矩形,
∴.
∴.
∴.
∴.
∴.
∴.
∴.
根据对称可得,.
∴.
∴四边形是矩形.
∴.
∴是的垂直平分线.
∴.
(3)
解:根据对称可得点与点的对称点分别为点.
作点关于的对称点,如图3.
由对称性得.
∴,点落在以点B为圆心,以AB为半径的弧AM上.
设弧交于点,过点作于.
由垂线段最短知.
∵,∴.
∴当点落在点处时,的面积最小.
即的面积最小.此时.
.
∴面积的最小值为4
21.(1);(2)32万部,最大值为6104万美元.
【解析】
(1)先由生产该款手机2万部并全部销售完时,年利润为704万美元,解得,然后由,将代入即可.
(2)当时利用二次函数的性质求解;当时,利用基本不等式求解,综上对比得到结论.
【详解】
(1)因为生产该款手机2万部并全部销售完时,年利润为704万美元.
所以,
解得,
当时, ,
当时, .
所以
(2)①当时, ,所以;
②当时, ,由于,
当且仅当,即时,取等号,所以此时的最大值为5760.
综合①②知,当,取得最大值为6104万美元.
【点睛】
思路点睛:应用题的基本解题步骤:
(1)根据实际问题抽象出函数的解析式,再利用基本不等式求得函数的最值;
(2)设变量时一般要把求最大值或最小值的变量定义为函数;
(3)解应用题时,要注意变量的实际意义及其取值范围;
(4)在应用基本不等式求函数最值时,若等号取不到,可利用函数的单调性求解.
22.(Ⅰ) ;(Ⅱ) ;(Ⅲ).
【解析】
【分析】
(Ⅰ)由对称轴方程为,可得,再利用图象过点求得,从而可得结果;(Ⅱ)将写成分段函数形式,分类讨论,结合二次函数的性质即可得结果;(Ⅲ)如果函数的图象上存在符合要求的点,设为,其中为正整数, 为自然数,则,可得,结合为正整数,为自然数,从而可得结果.
【详解】
(Ⅰ) ∵ 的对称轴方程为,∴ .
又的图象过点(1,13),∴ ,∴ .
∴ 的解析式为.
(Ⅱ) 由(Ⅰ)得:
结合图象可知:当,;
当,;
当,.
∴ 综上:
(Ⅲ)如果函数的图象上存在符合要求的点,设为,其中为正整数,
为自然数,则,
(法一)从而, 即.
注意到是质数,且,又,
所以只有, 解得:.
因此,函数的图象上存在符合要求的点,它的坐标为.
(法二)从而的偶数,∴ 的奇数
∴ 取验证得,当时符合
因此,函数的图象上存在符合要求的点,它的坐标为.
【点睛】
本题主要考查二次函数的解析式与分段函数的性质,考查了分类讨论思想,属于中档题. 分类讨论思想的常见类型
⑴问题中的变量或含有需讨论的参数的,要进行分类讨论的;
⑵问题中的条件是分类给出的;
⑶解题过程不能统一叙述,必须分类讨论的;
⑷涉及几何问题时,由几何元素的形状、位置的变化需要分类讨论的.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.我国古代数学家刘徽用“割圆术”将的值精确到小数点后七位,其结果领先世界1000多年.“割圆术”是指用圆的内接正多边形的周长来近似替代圆的周长,从正六边形起算,并依次倍增,使误差逐渐减小,如图所示,当圆的内接正多边形的边数为12时,由“割圆术”可得圆周率的近似值为( )
A. B. C. D.
2.如图所示几何体是由一个长方体和圆锥构成,则该几何体的俯视图可以为( )
A. B. C. D.
3.若关于x的方程x2+mx+1=0有两个不相等的实数根,则实数m的取值范围是
A.(﹣1,1) B.(﹣2,2) C.(﹣∞,﹣2)∪(2,+∞) D.(﹣∞,﹣1)∪(1,+∞)
4.《九章算术》中有如下问题:“今有勾五步,股一十二步,问勾中容圆,径几何 ”其大意:“已知直角三角形两直角边长分别为5步和12步,问其内切圆的直径为多少步 ”则其内切圆的直径的步数为( )
A.1 B.2 C.3 D.4
5.如图,已知是半圆的直径,A是延长线上一点,切半圆于点D,于点C,于点F,若,则的半径为( )
A.3.5 B.4 C. D.3.75
6.一只盒子中有个红球,9个白球,个黑球,每个球除颜色外都有相同.已知至少摸出17个球时其中一定有5个红球,至少摸出17个球时其中一定有8个相同颜色的球,则代数式的值为( )
A.7 B.6 C.5 D.4
7.如图,正方形和正方形的边长分别为3和1,点,分别在边,上,为的中点,连接,则的长为( )
A. B.2 C. D.
8.某人从上一层到二层需跨10级台阶. 他一步可能跨1级台阶,称为一阶步,也可能跨2级台阶,称为二阶步,最多能跨3级台阶,称为三阶步. 从一层上到二层他总共跨了6步,而且任何相邻两步均不同阶. 则他从一层到二层可能的不同过程共有( )种.
A.6 B.8 C.10 D.12
二、填空题
9.我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助这种分割方法所得的图形证明了勾股定理.如图所示的矩形由两个这样的图形拼成,若,则该矩形的面积为___________.
10.已知为等腰三角形,,边上的中线的长为7,则的面积为__________.
11.已知方程有两个负根,则k的取值集合为___________.
12.已知实数,满足方程,当时,的取值范围为________.
13.如图是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图中∠ACB=20°)时最为合适,已知货车车厢底部到地面的距离AB=1.5m,木板超出车厢部分AD=0.5m,则木板CD的长度为________.(参考数据:sin20°≈0.3420,cos20°≈0.9397,精确到0.1m).
14.如图,在等边中,分别为的中点,于点为的中点,连接,且,则的面积为__________.
15.如图,有一个边长不定的正方形,它的两个相对的顶点,分别在边长为1的正六边形一组平行的对边上,另外两个顶点,在正六边形内部(包括边界),则正方形边长的取值范围是___________.
16.若函数 在区间上为增函数,则的取值范围是______.
三、解答题
17.某班有甲、乙、丙三位学生在志愿者活动中表现优异,现从3人中选1人去参加全校表彰大会,有同学提议用如下方法:将4个编号为1,2,3,4的小球(形状、大小、质地都相同),放在一个不透明的袋中,按甲、乙、丙的顺序依次不放回地从袋中摸取一个小球,谁摸取的小球编号最大,谁就参加表彰大会.现用有序数组表示摸球的结果,例如表示甲、乙、丙摸取的小球编号分别为1,4,3.
(1)列出所有摸球的结果;
(2)求甲去参加表彰大会的概率,并判断该同学提议的方法是否公平.
18.已知关于的方程有两个实数根.
(1)求实数的取值范围;
(2)若满足,求实数的值.
19.如图,已知是的直径,弦与直径相交于点.点在外,作直线,且.
(1)求证:直线是的切线.
(2)若,,,求的长.
20.如图,在矩形中,是边上的一个动点,将四边形沿直线折叠,得到四边形,连接.
(1)若直线交于点,求证:;
(2)当时,求证:是等腰三角形;
(3)在点的运动过程中,求面积的最小值.
21.我国所需的高端芯片很大程度依赖于国外进口,“缺芯之痛”关乎产业安全、国家经济安全.如今,我国科技企业正在芯片自主研发之路中不断崛起.根据市场调查某手机品牌公司生产某款手机的年固定成本为40万美元,每生产1万部还需另投入16万美元.设该公司一年内共生产该款手机万部并全部销售完,每万部的销售收入为万美元,且当该公司一年内共生产该款手机2万部并全部销售完时,年利润为704万美元.
(1)写出年利润(万美元)关于年产量(万部)的函数解析式:
(2)当年产量为多少万部时,公司在该款手机的生产中所获得的利润最大 并求出最大利润.
22.已知二次函数的图象过点,且函数对称轴方程为.
(Ⅰ)求函数的解析式;
(Ⅱ)设函数,求在区间上的最小值;
(Ⅲ)探究:函数的图象上是否存在这样的点,使它的横坐标是正整数,纵坐标是一个完全平方数?如果存在,求出这样的点的坐标;如果不存在,请说明理由.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.A
【解析】
设圆的半径为,圆的内接12边形的边长为,将圆的周长近似等于12边形的周长即可求解.
【详解】
设圆的半径为,则圆的内接12边形的边长为,
周长为,
由,得.
故选:A.
【点睛】
本题考查了圆的面积公式,考查了基本运算能力,属于基础题.
2.C
【解析】
【详解】
解:根据俯视图的定义,可知这个几何体的内部是一个柱体,上面是个圆锥,因此俯视图为选C.被挡住的部分用虚线表示.
3.C
【解析】
【详解】
试题分析:利用题中条件:“关于x的方程x2+mx+1=0有两个不相等的实数根”由韦达定理的出m的关系式,解不等式即可.
解:∵关于x的方程x2+mx+1=0有两个不相等的实数根,
∴△>0,
即:m2﹣4>0,
解得:m∈(﹣∞,﹣2)∪(2,+∞).
故选C.
点评:本题考查一元二次方程的根的判别式与根的关系,属于基本运算的考查.
4.D
【解析】
【分析】
求出三角形的斜边,根据三角形面积自等,即可求出内切圆半径,进而可得结果.
【详解】
设内切圆半径为R,三角形斜边为 ,
所以,直径为4
故选:D
5.D
【解析】
根据图形,连接OD,作于点H,由切半圆于点D,得到,又,则,易证,得到,设,然后在中,利用勾股定理求解.
【详解】
如图所示:
连接OD,作于点H,
因为切半圆于点D,
所以,又,
所以,
所以,
又,
所以,
所以,
设,则,
在中,由勾股定理得,
解得,
故选:D
【点睛】
本题主要考查圆的切线的性质,切割线定理,勾股定理等面积法以及平行线段成比例定理,还考查了数形结合的思想方法,属于中档题.
6.D
【解析】
【分析】
根据“至少摸出17个球时其中一定有5个红球得到方程,求得;根据“至少摸出17个球时一定有8个相同色的球”,最坏的情况,这17个球中一定包含3个黑球,这样其余的14个球只有红球和白球.为了保证这14个球中一定有8个颜色相同的球,于是得到,(8为白球数,若,则会出现,不能保证8个同色),即可得到结论.
【详解】
“至少摸出17个球时其中一定有5个红球”:“一定”包含最坏的情况,即摸完所有的白球和黑球才摸到红球,
,
;
“至少摸出17个球时一定有8个相同颜色的球”:最坏的情况:这17个球中一定包含3个黑球.
这样其余的14个球只有红球和白球.
为了保证这14个球中一定有8个颜色相同的球,
,(8为白球数,若,则会出现,不能保证8个同色),
.
故选:D.
7.C
【解析】
【分析】
延长交于点,作于点,则是的中位线,求得的长和的长,在中利用勾股定理求解.
【详解】
延长交于点,作于点.
则.
是的中点,
是的中位线,
.
直角中,,
是等腰直角三角形,
即,
同理中,.
.
在中,.
故选:C.
8.C
【解析】
【详解】
按题意要求,不难验证这6步中不可能没有三阶步,也不可能有多于1个的三阶步. 因此,只能是1个三阶步,2个二阶步,3个一阶步.
为形象起见,以白、黑、红三种颜色的球来记录从一层到二层跨越10级台阶的过程:
白球表示一阶步,黑球表示二阶步,红球表示三阶步. 每一过程可表为3个白球、2个黑球、1个红球的一种同色球不相邻的排列.
下面分三种情形讨论.
(1)第1、第6球均为白球,则两黑球必分别位于中间白球的两侧. 此时,共有4个黑白球之间的空位放置红球. 所以,此种情况共有4种可能的不同排列.
(2)第1球不是白球.
(i)第1球为红球,则余下5球只有一种可能的排列;
(ii)若第1球为黑球,则余下5球因红、黑球的位置不同有两种不同的排列,此种情形共有3种不同排列.
(3)第6球不是白球,同(2),共有3种不同排列.
总之,按题意要求从一层到二层共有种可能的不同过程.
9.12
【解析】
设小正方形的边长为,在中由勾股定理得,则可求出面积.
【详解】
设小正方形的边长为,
,,
在中,,
即,即,
则该矩形的面积为.
故答案为:12.
10.
【解析】
【分析】
先设等腰三角形的腰长为,进而可得底边的长,再由余弦定理列出方程,即可求出,从而可得结果.
【详解】
设等腰三角形的腰长为,因为,所以,
由余弦定理可得:,
,
因为与互补,所以,即,
解得,
所以,所以
故答案为
【点睛】
本题主要考查解三角形的问,常用余弦定理和正弦定理来处理,属于基础题型.
11.
【解析】
【分析】
根据判别式和韦达定理列式可求出结果.
【详解】
设方程的两个负根为,
所以,解得,
故答案为:
12.
【解析】
可知表示直线上的点与点连线的斜率,即可求出.
【详解】
实数,满足方程,当时,
表示直线上的点与点连线的斜率,
设、为直线上的两个点,且,
的斜率为,的斜率为 ,
故的范围为,
故答案为:.
13.
【解析】
【分析】
根据的正弦函数和的长度求的长,再加上即可.
【详解】
解:由题意可知:.
在中,,
,
.
故答案为:.
14.
【解析】
【分析】
根据题意设正三角形边长为,连接,则,化简求得,根据勾股定理列方程,可求,即可求解三角形面积.
【详解】
连接
设
则
且
且
在中
可得方程
解得
故
故答案为:
【点睛】
本题考查正三角形性质,平行关系和垂直关系,基础题型.
15.
【解析】
【分析】
当正方形的顶点 在正六边形的边上时,正方形的边长的值最大,解直角三角形得到,当正方形的对角线在正六边形一组平行的对边的中点上时,正方形边长的值最小,是正方形的对角线,解直角三角形即可得到结论.
【详解】
①当正方形的对角线在正六边形一组平行的对边的中点上时,
正方形边长的值最小,是正方形的对角线,
,
,
②当正方形的四个顶点都在正六边形的边上时,正方形边长的值最大,是正方形的对角线,
建立下图直角坐标系,设时,正方形的边长最大,
,
,
设直线的解析式为,,,
,
,
直线的解析式为,
将代入得,
此时,取最大值,
,
正方形边长的取值范围是:,
故答案为:.
16.
【解析】
【详解】
设 .
由题设知,当 时,在区间上为减函数,即 ,所以a≥16,矛盾.
当 时,在区间上为增函数,即 .
因此,的取值范围为.
故答案为
17.(1)答案见解析(2),公平
【解析】
(1)一一列举出所有的摸球结果(基本事件)即可,
(2)找到甲摸取的小球编号最大的结果(基本事件),根据概率公式计算即可,并作出判断.
【详解】
(1)基本事件为(1,2,3),(1,2,4),(1,3,2),(1,3,4),(1,4,2),(1,4,3),(2,1,3),(2,1,4),(2,3,1),(2,3,4),(2,4,1),(2,4,3),(3,1,2),(3,1,4),(3,2,1),(3,2,4),(3,4,1),(3,4,2),(4,1,2),(4,1,3),(4,2,1),(4,2,3),(4,3,1),(4,3,2),基本事件的总数为24.
(2) 甲去参加表彰大会包含的基本事件为(3,1,2),(3,2,1),(4,1,2),(4,1,3),(4,2,1),(4,2,3),(4,3,1),(4,3,2),共8个基本事件,
所以甲去参加表彰大会的概率,
甲乙丙三名同学获胜的概率与其摸取的次序是无关,该方法是公平的.
18.(1)
(2)
【解析】
【分析】
(1)利用判别式的意义得到,然后解不等式即可;
(2)利用根与系数的关系得到,,利用得到,然后解方程后利用的范围确定的值.
(1)关于的方程有两个实数根,,解得.
(2)关于的方程有两个实数根,,,,,整理得,解得,,,的值为.
19.(1)证明见解析
(2)
【解析】
【分析】
(1)根据切线的判定即可得直线是的切线.
(2)根据直径所对圆周角是直角可得,根据,,即可求的长.
(1)证明:连接,是的直径,,即,,,,即,直线是的切线;
(2)过点作边的垂线交于点.,,,,,,在中,.
20.(1)证明见解析
(2)证明见解析
(3)4
【解析】
【分析】
(1)根据题意证明即可证明结论;
(2)分别过点作于点于点,进而根据几何关系证明是垂直平分线即可证明结论;
(3)作点关于的对称点,点落在以点B为圆心,以AB为半径的弧AM上.设弧交于点,过点作于,进而得当点落在点处时,的面积最小,再根据即可得答案.
(1)证明:∵四边形是矩形,
∴.
∴.
根据对称可得,
∴.
∴.
(2)
证明:如图2,分别过点作于点于点,
∵四边形是矩形,
∴.
∴.
∴.
∴.
∴.
∴.
∴.
根据对称可得,.
∴.
∴四边形是矩形.
∴.
∴是的垂直平分线.
∴.
(3)
解:根据对称可得点与点的对称点分别为点.
作点关于的对称点,如图3.
由对称性得.
∴,点落在以点B为圆心,以AB为半径的弧AM上.
设弧交于点,过点作于.
由垂线段最短知.
∵,∴.
∴当点落在点处时,的面积最小.
即的面积最小.此时.
.
∴面积的最小值为4
21.(1);(2)32万部,最大值为6104万美元.
【解析】
(1)先由生产该款手机2万部并全部销售完时,年利润为704万美元,解得,然后由,将代入即可.
(2)当时利用二次函数的性质求解;当时,利用基本不等式求解,综上对比得到结论.
【详解】
(1)因为生产该款手机2万部并全部销售完时,年利润为704万美元.
所以,
解得,
当时, ,
当时, .
所以
(2)①当时, ,所以;
②当时, ,由于,
当且仅当,即时,取等号,所以此时的最大值为5760.
综合①②知,当,取得最大值为6104万美元.
【点睛】
思路点睛:应用题的基本解题步骤:
(1)根据实际问题抽象出函数的解析式,再利用基本不等式求得函数的最值;
(2)设变量时一般要把求最大值或最小值的变量定义为函数;
(3)解应用题时,要注意变量的实际意义及其取值范围;
(4)在应用基本不等式求函数最值时,若等号取不到,可利用函数的单调性求解.
22.(Ⅰ) ;(Ⅱ) ;(Ⅲ).
【解析】
【分析】
(Ⅰ)由对称轴方程为,可得,再利用图象过点求得,从而可得结果;(Ⅱ)将写成分段函数形式,分类讨论,结合二次函数的性质即可得结果;(Ⅲ)如果函数的图象上存在符合要求的点,设为,其中为正整数, 为自然数,则,可得,结合为正整数,为自然数,从而可得结果.
【详解】
(Ⅰ) ∵ 的对称轴方程为,∴ .
又的图象过点(1,13),∴ ,∴ .
∴ 的解析式为.
(Ⅱ) 由(Ⅰ)得:
结合图象可知:当,;
当,;
当,.
∴ 综上:
(Ⅲ)如果函数的图象上存在符合要求的点,设为,其中为正整数,
为自然数,则,
(法一)从而, 即.
注意到是质数,且,又,
所以只有, 解得:.
因此,函数的图象上存在符合要求的点,它的坐标为.
(法二)从而的偶数,∴ 的奇数
∴ 取验证得,当时符合
因此,函数的图象上存在符合要求的点,它的坐标为.
【点睛】
本题主要考查二次函数的解析式与分段函数的性质,考查了分类讨论思想,属于中档题. 分类讨论思想的常见类型
⑴问题中的变量或含有需讨论的参数的,要进行分类讨论的;
⑵问题中的条件是分类给出的;
⑶解题过程不能统一叙述,必须分类讨论的;
⑷涉及几何问题时,由几何元素的形状、位置的变化需要分类讨论的.
答案第1页,共2页
答案第1页,共2页
同课章节目录
