2022-2023学年新高一入学考试数学试题2(福建)(Word版含解析)
文档属性
| 名称 | 2022-2023学年新高一入学考试数学试题2(福建)(Word版含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 其它版本 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 00:00:00 | ||
图片预览




文档简介
2022-2023学年新高一入学考试数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若,,则的值为( )
A. B. C. D.
2.如图,为一圆柱切削后的几何体及其正视图,则相应的侧视图可以是
A. B. C. D.
3.若数使关于的分式方程的解为正数,且使关于的不等式组的解集为,则符合条件的所有整数的和为( )
A.10 B.12 C.14 D.9
4.正方形、正方形和正方形的位置如图所示,点在线段上,正方形的边长为4,则的面积为( )
A.10 B.12 C.14 D.16
5.如图,正三角形的边长为4,过点B的直线,且与关于直线l对称,D为线段上一动点,则的最小值是( )
A. B. C.8 D.
6.一只盒子中有个红球,9个白球,个黑球,每个球除颜色外都有相同.已知至少摸出17个球时其中一定有5个红球,至少摸出17个球时其中一定有8个相同颜色的球,则代数式的值为( )
A.7 B.6 C.5 D.4
7.如图,是⊙的直径, 点是⊙上一点,与过点的切线垂直,垂足为,直线与的延长线交于点,弦平分,交于点,连接,.下列四个结论:①平分;②;③若,则阴影部分的面积为;④若,则.其中正确的是( )
A.①② B.③④ C.①②④ D.①②③
8.某人从上一层到二层需跨10级台阶. 他一步可能跨1级台阶,称为一阶步,也可能跨2级台阶,称为二阶步,最多能跨3级台阶,称为三阶步. 从一层上到二层他总共跨了6步,而且任何相邻两步均不同阶. 则他从一层到二层可能的不同过程共有( )种.
A.6 B.8 C.10 D.12
二、填空题
9.已知,则___________.
10.一艘轮船从港口A处出发,以15海里小时的速度沿着北偏西的方向直线航行,在港口A处测得灯塔M在北偏东方向,航行40分钟后,轮船与灯塔的距离是海里,则灯塔M与港口A的距离为______海里.
11.滴滴快车是一种便捷的出行工具,计价规则如表:
计费项目 里程费 时长费 远途费
单价 1.8元公里 0.3元分钟 0.8元公里
注:车费由里程费 时长费 远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收0.8元.
小王与小张各自乘坐滴滴快车,行车里程分别为6公里与8.5公里.如果下车时两人所付车费相同,那么这两辆滴滴快车的行车时间相差___________.
12.已知实数,满足方程,当时,的取值范围为________.
13.如图是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图中∠ACB=20°)时最为合适,已知货车车厢底部到地面的距离AB=1.5m,木板超出车厢部分AD=0.5m,则木板CD的长度为________.(参考数据:sin20°≈0.3420,cos20°≈0.9397,精确到0.1m).
14.如图,在中,,,,,则________.
15.如图,有一个边长不定的正方形,它的两个相对的顶点,分别在边长为1的正六边形一组平行的对边上,另外两个顶点,在正六边形内部(包括边界),则正方形边长的取值范围是___________.
16.若函数f(x)=x2-2ax+a2-4在区间[a-2,a2](a>0)上的值域为[-4,0],则实数a的取值范围为________.
三、解答题
17.2015年我国将加快阶梯水价推行,原则是“保基本、建机制、促节约”,其中“保基本”是指保证至少80%的居民用户用水价格不变.为响应国家政策,制定合理的阶梯用水价格,某城市采用简单随机抽样的方法分别从郊区和城区抽取5户和20户居民的年人均用水量进行调研,抽取的数据的茎叶图如下(单位:吨):
(1)在郊区的这5户居民中随机抽取2户,求其年人均用水量都不超过30吨的概率;
(2)设该城市郊区和城区的居民户数比为,现将年人均用水量不超过30吨的用户定义为第一阶梯用户,并保证这一梯次的居民用户用水价格保持不变.试根据样本估计总体的思想,分析此方案是否符合国家“保基本”政策.
18.已知关于的方程有两个实数根.
(1)求实数的取值范围;
(2)若满足,求实数的值.
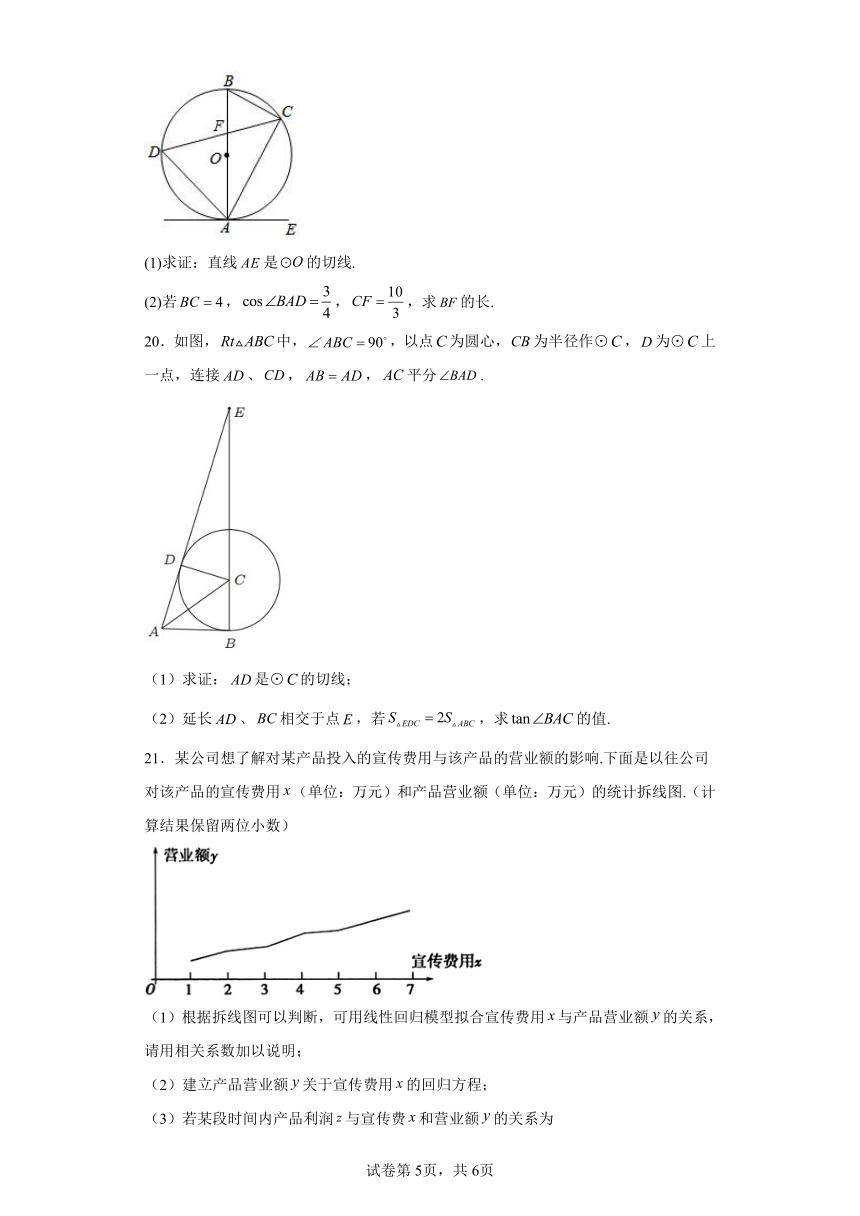
19.如图,已知是的直径,弦与直径相交于点.点在外,作直线,且.
(1)求证:直线是的切线.
(2)若,,,求的长.
20.如图,中,,以点为圆心,为半径作⊙,为⊙上一点,连接、,,平分.
(1)求证:是⊙的切线;
(2)延长、相交于点,若,求的值.
21.某公司想了解对某产品投入的宣传费用与该产品的营业额的影响.下面是以往公司对该产品的宣传费用(单位:万元)和产品营业额(单位:万元)的统计拆线图.(计算结果保留两位小数)
(1)根据拆线图可以判断,可用线性回归模型拟合宣传费用与产品营业额的关系,请用相关系数加以说明;
(2)建立产品营业额关于宣传费用的回归方程;
(3)若某段时间内产品利润与宣传费和营业额的关系为应投入宣传费多少万元才能使利润最大,并求最大利润.
参考数据:,,,,
参考公式:相关系数,
回归方程中斜率和截距的最小二乘法估计公式分别为,.
22.已知二次函数满足:①当时,且;②当时,;③在上的最小值为0.
(1)求a,b,c的值;
(2)试求最大的,使得存在,只要,都有.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
依题意可得,再代入已知条件计算可得.
【详解】
解:,,
.
故选:D.
2.B
【解析】
【分析】
三视图是对一个物体从一个三个不同的侧面进行正投影得到的,三个视图间存在长对正,高平齐,宽相等的对应关系,在三视图中不可见的轮廓用虚线表示.
【详解】
根据题意以及已知图形:由主视图得出主视方向,左视图应该是从实物图的左边进行正投影,右边的轮廓为不可见轮廓,所以要用虚线表示,故B正确.
故选:B.
【点睛】
考查正投影,以及三视图的作图知识,本题属于中档题.
3.D
【解析】
【分析】
根据分式方程的解为正数即可得出且,根据不等式组的解集为,即可得出,找出且中所有的整数,将其相加即可得出结论.
【详解】
解:分式方程的解为且,
关于的分式方程的解为正数,
且,
且.
不等式组整理得,
关于的不等式组的解集为,
.
且.
符合条件的所有整数为 0 1 2 4 5,它们的和为9.
故选:D.
4.D
【解析】
【分析】
根据题意,连接,则,进而得,,再计算面积即可得答案.
【详解】
解:如图,连接,则,
所以,在梯形中,(等底等高),
在梯形中,(等底等高)
所以,.
故选:D
5.C
【解析】
连接,先根据轴对称性得出也是边长为4的等边三角形,再根据等边三角形的性质,三角形全等的判定定理和性质得出,然后根据三角形的三边关系定理、两点之间线段最短找出取得最小值时点D的位置,由此可以得出答案.
【详解】
如图,连接,
正的边长为4,
,
与关于直线l对称,
也是边长为4的等边三角形,
,
,
在和中,,
,,
,
,
,
由三角形的三边关系定理、两点之间线段最短可知,
当点D与点B重合,即点共线时,
取得最小值,
最小值为.
故选:C.
【点睛】
本题考查了轴对称的性质、等边三角形的性质、三角形全等的判定定理与性质、两点之间线段最短等知识点,属于基础题.
6.D
【解析】
【分析】
根据“至少摸出17个球时其中一定有5个红球得到方程,求得;根据“至少摸出17个球时一定有8个相同色的球”,最坏的情况,这17个球中一定包含3个黑球,这样其余的14个球只有红球和白球.为了保证这14个球中一定有8个颜色相同的球,于是得到,(8为白球数,若,则会出现,不能保证8个同色),即可得到结论.
【详解】
“至少摸出17个球时其中一定有5个红球”:“一定”包含最坏的情况,即摸完所有的白球和黑球才摸到红球,
,
;
“至少摸出17个球时一定有8个相同颜色的球”:最坏的情况:这17个球中一定包含3个黑球.
这样其余的14个球只有红球和白球.
为了保证这14个球中一定有8个颜色相同的球,
,(8为白球数,若,则会出现,不能保证8个同色),
.
故选:D.
7.C
【解析】
【分析】
连接,结合切线的性质得,进而根据平行线的性质判断①;根据几何关系证明,再根据得判断②;连接,根据几何关系证明是等边三角形,进而计算阴影部分面积判断③;由得,再设,则,根据解得,进而可判断④;
【详解】
解:对于①,连接,,,
∵是圆的切线,,∴,∴,
∴,即平分,故①正确;
对于②,∵是直径,∴,,
又,,
又,,
,,
∵是公共角,,,
,即,故②正确;
对于③,连接,∵,∴,∴,
又∵是直径,∴,∴,∴,
∵是切线,∴,∵,∴是的中线,
∴,即是等边三角形,∴,
∴,
∴ 阴影部分面积为,故③错误;
对于④,,∴,,
设,则,,,解得,
,,故④正确.
故选:C
8.C
【解析】
【详解】
按题意要求,不难验证这6步中不可能没有三阶步,也不可能有多于1个的三阶步. 因此,只能是1个三阶步,2个二阶步,3个一阶步.
为形象起见,以白、黑、红三种颜色的球来记录从一层到二层跨越10级台阶的过程:
白球表示一阶步,黑球表示二阶步,红球表示三阶步. 每一过程可表为3个白球、2个黑球、1个红球的一种同色球不相邻的排列.
下面分三种情形讨论.
(1)第1、第6球均为白球,则两黑球必分别位于中间白球的两侧. 此时,共有4个黑白球之间的空位放置红球. 所以,此种情况共有4种可能的不同排列.
(2)第1球不是白球.
(i)第1球为红球,则余下5球只有一种可能的排列;
(ii)若第1球为黑球,则余下5球因红、黑球的位置不同有两种不同的排列,此种情形共有3种不同排列.
(3)第6球不是白球,同(2),共有3种不同排列.
总之,按题意要求从一层到二层共有种可能的不同过程.
9.
【解析】
【分析】
原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把的值代入计算即可求出值.
【详解】
解:原式
,
当时,原式.
故答案为:.
10.5
【解析】
【分析】
在中,利用正弦定理计算得出是直角三角形,再计算即可.
【详解】
设轮船航行40分钟后到达B点,由题意可知海里,海里,,
在中,由正弦定理可得,
即,解得,所以,
在中,,所以海里.
故答案为:5.
【点睛】
本题考查正弦定理在解三角形中的应用,属于基础题.
11.19分钟
【解析】
【分析】
设小王的行车时间为分钟,小张的行车时间为分钟,根据题意列出小王和小张车费的代数式,两者相等,计算可得出时间差.
【详解】
设小王的行车时间为分钟,小张的行车时间为分钟,依题可得:
,
,
,
.
故这两辆滴滴快车的行车时间相差19分钟.
故答案是:19分钟.
12.
【解析】
可知表示直线上的点与点连线的斜率,即可求出.
【详解】
实数,满足方程,当时,
表示直线上的点与点连线的斜率,
设、为直线上的两个点,且,
的斜率为,的斜率为 ,
故的范围为,
故答案为:.
13.
【解析】
【分析】
根据的正弦函数和的长度求的长,再加上即可.
【详解】
解:由题意可知:.
在中,,
,
.
故答案为:.
14.70°
【解析】
由,可得,再结合等腰三角形及内角和为的条件可得解.
【详解】
,
,
又,,
,
,
,
,
故答案为:70°
【点睛】
本题考查了全等三角形的判定以及全等三角形的性质、等腰三角形的性质以及三角形内角和定理;利用题目中隐含的条件平角解题是解决本题得到关键.
15.
【解析】
【分析】
当正方形的顶点 在正六边形的边上时,正方形的边长的值最大,解直角三角形得到,当正方形的对角线在正六边形一组平行的对边的中点上时,正方形边长的值最小,是正方形的对角线,解直角三角形即可得到结论.
【详解】
①当正方形的对角线在正六边形一组平行的对边的中点上时,
正方形边长的值最小,是正方形的对角线,
,
,
②当正方形的四个顶点都在正六边形的边上时,正方形边长的值最大,是正方形的对角线,
建立下图直角坐标系,设时,正方形的边长最大,
,
,
设直线的解析式为,,,
,
,
直线的解析式为,
将代入得,
此时,取最大值,
,
正方形边长的取值范围是:,
故答案为:.
16.[1,2]
【解析】
【详解】
∵f(x)=x2-2ax+a2-4=(x-a)2-4,f(a)=-4,f(a-2)=0,f(x)在区间[a-2,a2]上的值域为[-4,0],f(x)的图像为开口向上的拋物线.
∴,解得-1≤a≤0或1≤a≤2.结合a>0,得1≤a≤2.
∴a的取值范围为[1,2].
17.(1)(2)符合
【解析】
【分析】
:(1)先列举出从5户郊区居民用户中随机抽取2户,其年人均用水量构成的所有基本事件,再列举其中年人均用水量都不超过30吨的基本事件,最后计算即可.
(2)设该城市郊区的居民用户数为,则其城区的居民用户数为5a.依题意计算该城市年人均用水量不超过30吨的居民用户的百分率.
【详解】
解:(1)从5户郊区居民用户中随机抽取2户,其年人均用水量构成的所有基本事件是:
(19,25),(19,28),(19,32),(19,34),(25,28),(25,32),(25,34),(28,32),(28,34),
(32,34)共10个.
其中年人均用水量都不超过30吨的基本事件是:(19,25),(19,28),(25,28)共3个.
设“从5户郊区居民用户中随机抽取2户,其年人均用水量都不超过30吨”的事件为,则所求的概率为.
(2)设该城市郊区的居民用户数为,则其城区的居民用户数为5a.依题意,该城市年人均用水量不超过30吨的居民用户的百分率为:
.故此方案符合国家“保基本”政策.
【点睛】
本题考查了古典概型在实际生活中的应用,要紧扣题意从题目中抽象出数学计算的模型.
18.(1)
(2)
【解析】
【分析】
(1)利用判别式的意义得到,然后解不等式即可;
(2)利用根与系数的关系得到,,利用得到,然后解方程后利用的范围确定的值.
(1)关于的方程有两个实数根,,解得.
(2)关于的方程有两个实数根,,,,,整理得,解得,,,的值为.
19.(1)证明见解析
(2)
【解析】
【分析】
(1)根据切线的判定即可得直线是的切线.
(2)根据直径所对圆周角是直角可得,根据,,即可求的长.
(1)证明:连接,是的直径,,即,,,,即,直线是的切线;
(2)过点作边的垂线交于点.,,,,,,在中,.
20.(1)证明见解析;(2).
【解析】
【分析】
(1)证明,可得出,即可证得结论成立;
(2)由(1)可得,根据已知条件得出,,由可得出,由此可计算得出的值.
【详解】
(1)因为,,,所以,,
所以,,即,
又因为为⊙上一点,所以,是⊙的切线;
(2)由(1)可知,,,
因为,则,,
,
因为,则,
,则,
所以,,,
在中,,故.
21.(1),说明见解析;(2);(3)投入宣传费为万元时,可获得最大利润为万元.
【解析】
【分析】
(1)计算出相关系数的值,根据相关系数的值进行说明即可;
(2)根据已知数据和公式分别求解出回归方程中的参数的值,则回归方程可求;
(3)根据回归方程表示出,然后利用二次函数的性质分析何时取最大值,并计算出最大利润的值.
【详解】
(1)因为,所以,
所以,
因为的相关系数近似为,
说明与的线性相关程度非常高,
从而可以用线性回归模型拟合与的关系;
(2)因为,
所以,所以,
所以产品营业额关于宣传费用的回归方程为:;
(3)因为,
所以,
当时,有最大值,且,
即投入宣传费为万元时,可获得最大利润为万元.
22.(1),,
(2)的最大值为9
【解析】
【分析】
(1)根据题意可得函数的图象关于对称,,,即可求出;
(2)令可得,取,可得,设,求出最大值即可.
(1)
由可得函数的图象关于对称,所以,即,
由③可得,时,,即,
由①得,由②得,故,即,
则可解得,,,,
∴;
(2)
假设存在,只要,就有,
令,可得,解得,
对固定的,取,可得,
即,解得,,
设,则,
令,设对称轴为,
∴当时有最大值9,
∴的最大值为9.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.若,,则的值为( )
A. B. C. D.
2.如图,为一圆柱切削后的几何体及其正视图,则相应的侧视图可以是
A. B. C. D.
3.若数使关于的分式方程的解为正数,且使关于的不等式组的解集为,则符合条件的所有整数的和为( )
A.10 B.12 C.14 D.9
4.正方形、正方形和正方形的位置如图所示,点在线段上,正方形的边长为4,则的面积为( )
A.10 B.12 C.14 D.16
5.如图,正三角形的边长为4,过点B的直线,且与关于直线l对称,D为线段上一动点,则的最小值是( )
A. B. C.8 D.
6.一只盒子中有个红球,9个白球,个黑球,每个球除颜色外都有相同.已知至少摸出17个球时其中一定有5个红球,至少摸出17个球时其中一定有8个相同颜色的球,则代数式的值为( )
A.7 B.6 C.5 D.4
7.如图,是⊙的直径, 点是⊙上一点,与过点的切线垂直,垂足为,直线与的延长线交于点,弦平分,交于点,连接,.下列四个结论:①平分;②;③若,则阴影部分的面积为;④若,则.其中正确的是( )
A.①② B.③④ C.①②④ D.①②③
8.某人从上一层到二层需跨10级台阶. 他一步可能跨1级台阶,称为一阶步,也可能跨2级台阶,称为二阶步,最多能跨3级台阶,称为三阶步. 从一层上到二层他总共跨了6步,而且任何相邻两步均不同阶. 则他从一层到二层可能的不同过程共有( )种.
A.6 B.8 C.10 D.12
二、填空题
9.已知,则___________.
10.一艘轮船从港口A处出发,以15海里小时的速度沿着北偏西的方向直线航行,在港口A处测得灯塔M在北偏东方向,航行40分钟后,轮船与灯塔的距离是海里,则灯塔M与港口A的距离为______海里.
11.滴滴快车是一种便捷的出行工具,计价规则如表:
计费项目 里程费 时长费 远途费
单价 1.8元公里 0.3元分钟 0.8元公里
注:车费由里程费 时长费 远途费三部分构成,其中里程费按行车的实际里程计算;时长费按行车的实际时间计算;远途费的收取方式为:行车里程7公里以内(含7公里)不收远途费,超过7公里的,超出部分每公里收0.8元.
小王与小张各自乘坐滴滴快车,行车里程分别为6公里与8.5公里.如果下车时两人所付车费相同,那么这两辆滴滴快车的行车时间相差___________.
12.已知实数,满足方程,当时,的取值范围为________.
13.如图是工人将货物搬运上货车常用的方法,把一块木板斜靠在货车车厢的尾部,形成一个斜坡,货物通过斜坡进行搬运.根据经验,木板与地面的夹角为20°(即图中∠ACB=20°)时最为合适,已知货车车厢底部到地面的距离AB=1.5m,木板超出车厢部分AD=0.5m,则木板CD的长度为________.(参考数据:sin20°≈0.3420,cos20°≈0.9397,精确到0.1m).
14.如图,在中,,,,,则________.
15.如图,有一个边长不定的正方形,它的两个相对的顶点,分别在边长为1的正六边形一组平行的对边上,另外两个顶点,在正六边形内部(包括边界),则正方形边长的取值范围是___________.
16.若函数f(x)=x2-2ax+a2-4在区间[a-2,a2](a>0)上的值域为[-4,0],则实数a的取值范围为________.
三、解答题
17.2015年我国将加快阶梯水价推行,原则是“保基本、建机制、促节约”,其中“保基本”是指保证至少80%的居民用户用水价格不变.为响应国家政策,制定合理的阶梯用水价格,某城市采用简单随机抽样的方法分别从郊区和城区抽取5户和20户居民的年人均用水量进行调研,抽取的数据的茎叶图如下(单位:吨):
(1)在郊区的这5户居民中随机抽取2户,求其年人均用水量都不超过30吨的概率;
(2)设该城市郊区和城区的居民户数比为,现将年人均用水量不超过30吨的用户定义为第一阶梯用户,并保证这一梯次的居民用户用水价格保持不变.试根据样本估计总体的思想,分析此方案是否符合国家“保基本”政策.
18.已知关于的方程有两个实数根.
(1)求实数的取值范围;
(2)若满足,求实数的值.
19.如图,已知是的直径,弦与直径相交于点.点在外,作直线,且.
(1)求证:直线是的切线.
(2)若,,,求的长.
20.如图,中,,以点为圆心,为半径作⊙,为⊙上一点,连接、,,平分.
(1)求证:是⊙的切线;
(2)延长、相交于点,若,求的值.
21.某公司想了解对某产品投入的宣传费用与该产品的营业额的影响.下面是以往公司对该产品的宣传费用(单位:万元)和产品营业额(单位:万元)的统计拆线图.(计算结果保留两位小数)
(1)根据拆线图可以判断,可用线性回归模型拟合宣传费用与产品营业额的关系,请用相关系数加以说明;
(2)建立产品营业额关于宣传费用的回归方程;
(3)若某段时间内产品利润与宣传费和营业额的关系为应投入宣传费多少万元才能使利润最大,并求最大利润.
参考数据:,,,,
参考公式:相关系数,
回归方程中斜率和截距的最小二乘法估计公式分别为,.
22.已知二次函数满足:①当时,且;②当时,;③在上的最小值为0.
(1)求a,b,c的值;
(2)试求最大的,使得存在,只要,都有.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.D
【解析】
【分析】
依题意可得,再代入已知条件计算可得.
【详解】
解:,,
.
故选:D.
2.B
【解析】
【分析】
三视图是对一个物体从一个三个不同的侧面进行正投影得到的,三个视图间存在长对正,高平齐,宽相等的对应关系,在三视图中不可见的轮廓用虚线表示.
【详解】
根据题意以及已知图形:由主视图得出主视方向,左视图应该是从实物图的左边进行正投影,右边的轮廓为不可见轮廓,所以要用虚线表示,故B正确.
故选:B.
【点睛】
考查正投影,以及三视图的作图知识,本题属于中档题.
3.D
【解析】
【分析】
根据分式方程的解为正数即可得出且,根据不等式组的解集为,即可得出,找出且中所有的整数,将其相加即可得出结论.
【详解】
解:分式方程的解为且,
关于的分式方程的解为正数,
且,
且.
不等式组整理得,
关于的不等式组的解集为,
.
且.
符合条件的所有整数为 0 1 2 4 5,它们的和为9.
故选:D.
4.D
【解析】
【分析】
根据题意,连接,则,进而得,,再计算面积即可得答案.
【详解】
解:如图,连接,则,
所以,在梯形中,(等底等高),
在梯形中,(等底等高)
所以,.
故选:D
5.C
【解析】
连接,先根据轴对称性得出也是边长为4的等边三角形,再根据等边三角形的性质,三角形全等的判定定理和性质得出,然后根据三角形的三边关系定理、两点之间线段最短找出取得最小值时点D的位置,由此可以得出答案.
【详解】
如图,连接,
正的边长为4,
,
与关于直线l对称,
也是边长为4的等边三角形,
,
,
在和中,,
,,
,
,
,
由三角形的三边关系定理、两点之间线段最短可知,
当点D与点B重合,即点共线时,
取得最小值,
最小值为.
故选:C.
【点睛】
本题考查了轴对称的性质、等边三角形的性质、三角形全等的判定定理与性质、两点之间线段最短等知识点,属于基础题.
6.D
【解析】
【分析】
根据“至少摸出17个球时其中一定有5个红球得到方程,求得;根据“至少摸出17个球时一定有8个相同色的球”,最坏的情况,这17个球中一定包含3个黑球,这样其余的14个球只有红球和白球.为了保证这14个球中一定有8个颜色相同的球,于是得到,(8为白球数,若,则会出现,不能保证8个同色),即可得到结论.
【详解】
“至少摸出17个球时其中一定有5个红球”:“一定”包含最坏的情况,即摸完所有的白球和黑球才摸到红球,
,
;
“至少摸出17个球时一定有8个相同颜色的球”:最坏的情况:这17个球中一定包含3个黑球.
这样其余的14个球只有红球和白球.
为了保证这14个球中一定有8个颜色相同的球,
,(8为白球数,若,则会出现,不能保证8个同色),
.
故选:D.
7.C
【解析】
【分析】
连接,结合切线的性质得,进而根据平行线的性质判断①;根据几何关系证明,再根据得判断②;连接,根据几何关系证明是等边三角形,进而计算阴影部分面积判断③;由得,再设,则,根据解得,进而可判断④;
【详解】
解:对于①,连接,,,
∵是圆的切线,,∴,∴,
∴,即平分,故①正确;
对于②,∵是直径,∴,,
又,,
又,,
,,
∵是公共角,,,
,即,故②正确;
对于③,连接,∵,∴,∴,
又∵是直径,∴,∴,∴,
∵是切线,∴,∵,∴是的中线,
∴,即是等边三角形,∴,
∴,
∴ 阴影部分面积为,故③错误;
对于④,,∴,,
设,则,,,解得,
,,故④正确.
故选:C
8.C
【解析】
【详解】
按题意要求,不难验证这6步中不可能没有三阶步,也不可能有多于1个的三阶步. 因此,只能是1个三阶步,2个二阶步,3个一阶步.
为形象起见,以白、黑、红三种颜色的球来记录从一层到二层跨越10级台阶的过程:
白球表示一阶步,黑球表示二阶步,红球表示三阶步. 每一过程可表为3个白球、2个黑球、1个红球的一种同色球不相邻的排列.
下面分三种情形讨论.
(1)第1、第6球均为白球,则两黑球必分别位于中间白球的两侧. 此时,共有4个黑白球之间的空位放置红球. 所以,此种情况共有4种可能的不同排列.
(2)第1球不是白球.
(i)第1球为红球,则余下5球只有一种可能的排列;
(ii)若第1球为黑球,则余下5球因红、黑球的位置不同有两种不同的排列,此种情形共有3种不同排列.
(3)第6球不是白球,同(2),共有3种不同排列.
总之,按题意要求从一层到二层共有种可能的不同过程.
9.
【解析】
【分析】
原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把的值代入计算即可求出值.
【详解】
解:原式
,
当时,原式.
故答案为:.
10.5
【解析】
【分析】
在中,利用正弦定理计算得出是直角三角形,再计算即可.
【详解】
设轮船航行40分钟后到达B点,由题意可知海里,海里,,
在中,由正弦定理可得,
即,解得,所以,
在中,,所以海里.
故答案为:5.
【点睛】
本题考查正弦定理在解三角形中的应用,属于基础题.
11.19分钟
【解析】
【分析】
设小王的行车时间为分钟,小张的行车时间为分钟,根据题意列出小王和小张车费的代数式,两者相等,计算可得出时间差.
【详解】
设小王的行车时间为分钟,小张的行车时间为分钟,依题可得:
,
,
,
.
故这两辆滴滴快车的行车时间相差19分钟.
故答案是:19分钟.
12.
【解析】
可知表示直线上的点与点连线的斜率,即可求出.
【详解】
实数,满足方程,当时,
表示直线上的点与点连线的斜率,
设、为直线上的两个点,且,
的斜率为,的斜率为 ,
故的范围为,
故答案为:.
13.
【解析】
【分析】
根据的正弦函数和的长度求的长,再加上即可.
【详解】
解:由题意可知:.
在中,,
,
.
故答案为:.
14.70°
【解析】
由,可得,再结合等腰三角形及内角和为的条件可得解.
【详解】
,
,
又,,
,
,
,
,
故答案为:70°
【点睛】
本题考查了全等三角形的判定以及全等三角形的性质、等腰三角形的性质以及三角形内角和定理;利用题目中隐含的条件平角解题是解决本题得到关键.
15.
【解析】
【分析】
当正方形的顶点 在正六边形的边上时,正方形的边长的值最大,解直角三角形得到,当正方形的对角线在正六边形一组平行的对边的中点上时,正方形边长的值最小,是正方形的对角线,解直角三角形即可得到结论.
【详解】
①当正方形的对角线在正六边形一组平行的对边的中点上时,
正方形边长的值最小,是正方形的对角线,
,
,
②当正方形的四个顶点都在正六边形的边上时,正方形边长的值最大,是正方形的对角线,
建立下图直角坐标系,设时,正方形的边长最大,
,
,
设直线的解析式为,,,
,
,
直线的解析式为,
将代入得,
此时,取最大值,
,
正方形边长的取值范围是:,
故答案为:.
16.[1,2]
【解析】
【详解】
∵f(x)=x2-2ax+a2-4=(x-a)2-4,f(a)=-4,f(a-2)=0,f(x)在区间[a-2,a2]上的值域为[-4,0],f(x)的图像为开口向上的拋物线.
∴,解得-1≤a≤0或1≤a≤2.结合a>0,得1≤a≤2.
∴a的取值范围为[1,2].
17.(1)(2)符合
【解析】
【分析】
:(1)先列举出从5户郊区居民用户中随机抽取2户,其年人均用水量构成的所有基本事件,再列举其中年人均用水量都不超过30吨的基本事件,最后计算即可.
(2)设该城市郊区的居民用户数为,则其城区的居民用户数为5a.依题意计算该城市年人均用水量不超过30吨的居民用户的百分率.
【详解】
解:(1)从5户郊区居民用户中随机抽取2户,其年人均用水量构成的所有基本事件是:
(19,25),(19,28),(19,32),(19,34),(25,28),(25,32),(25,34),(28,32),(28,34),
(32,34)共10个.
其中年人均用水量都不超过30吨的基本事件是:(19,25),(19,28),(25,28)共3个.
设“从5户郊区居民用户中随机抽取2户,其年人均用水量都不超过30吨”的事件为,则所求的概率为.
(2)设该城市郊区的居民用户数为,则其城区的居民用户数为5a.依题意,该城市年人均用水量不超过30吨的居民用户的百分率为:
.故此方案符合国家“保基本”政策.
【点睛】
本题考查了古典概型在实际生活中的应用,要紧扣题意从题目中抽象出数学计算的模型.
18.(1)
(2)
【解析】
【分析】
(1)利用判别式的意义得到,然后解不等式即可;
(2)利用根与系数的关系得到,,利用得到,然后解方程后利用的范围确定的值.
(1)关于的方程有两个实数根,,解得.
(2)关于的方程有两个实数根,,,,,整理得,解得,,,的值为.
19.(1)证明见解析
(2)
【解析】
【分析】
(1)根据切线的判定即可得直线是的切线.
(2)根据直径所对圆周角是直角可得,根据,,即可求的长.
(1)证明:连接,是的直径,,即,,,,即,直线是的切线;
(2)过点作边的垂线交于点.,,,,,,在中,.
20.(1)证明见解析;(2).
【解析】
【分析】
(1)证明,可得出,即可证得结论成立;
(2)由(1)可得,根据已知条件得出,,由可得出,由此可计算得出的值.
【详解】
(1)因为,,,所以,,
所以,,即,
又因为为⊙上一点,所以,是⊙的切线;
(2)由(1)可知,,,
因为,则,,
,
因为,则,
,则,
所以,,,
在中,,故.
21.(1),说明见解析;(2);(3)投入宣传费为万元时,可获得最大利润为万元.
【解析】
【分析】
(1)计算出相关系数的值,根据相关系数的值进行说明即可;
(2)根据已知数据和公式分别求解出回归方程中的参数的值,则回归方程可求;
(3)根据回归方程表示出,然后利用二次函数的性质分析何时取最大值,并计算出最大利润的值.
【详解】
(1)因为,所以,
所以,
因为的相关系数近似为,
说明与的线性相关程度非常高,
从而可以用线性回归模型拟合与的关系;
(2)因为,
所以,所以,
所以产品营业额关于宣传费用的回归方程为:;
(3)因为,
所以,
当时,有最大值,且,
即投入宣传费为万元时,可获得最大利润为万元.
22.(1),,
(2)的最大值为9
【解析】
【分析】
(1)根据题意可得函数的图象关于对称,,,即可求出;
(2)令可得,取,可得,设,求出最大值即可.
(1)
由可得函数的图象关于对称,所以,即,
由③可得,时,,即,
由①得,由②得,故,即,
则可解得,,,,
∴;
(2)
假设存在,只要,就有,
令,可得,解得,
对固定的,取,可得,
即,解得,,
设,则,
令,设对称轴为,
∴当时有最大值9,
∴的最大值为9.
答案第1页,共2页
答案第1页,共2页
同课章节目录
