11.3.2 多边形的内角和 课件(共24张PPT)
文档属性
| 名称 | 11.3.2 多边形的内角和 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-02 00:00:00 | ||
图片预览



文档简介
(共24张PPT)
11.3 多边形及其内角和
11.3.2 多边形的内角和
精品同步教学课件
情景引入
思考:你知道正六边形的内角和是多少吗?
问题2 你知道长方形和正方形的内角和是多少度吗?
问题1 三角形内角和是多少度?
三角形内角和 是180°.
都是360°.
问题3 猜想任意四边形的内角和是多少度?
多边形的内角和
一
猜想:四边形ABCD的内角和是360°.
问题4 你能用以前学过的知识说明一下你的结论吗?
猜想与证明
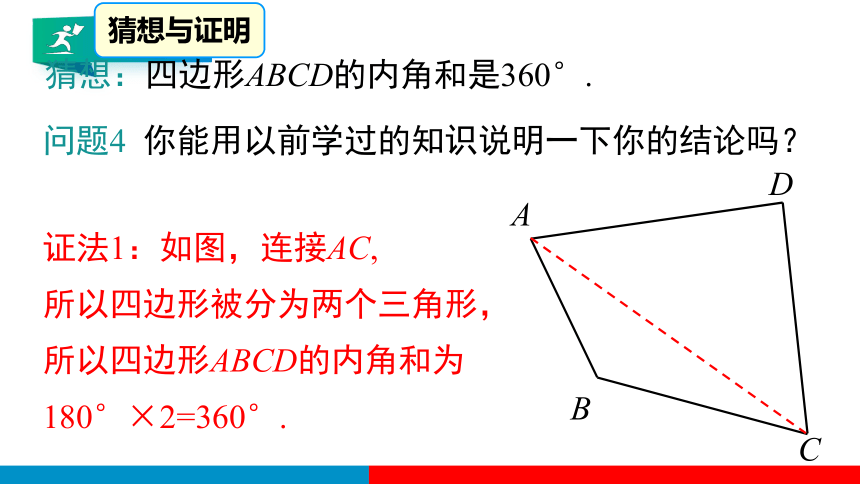
证法1:如图,连接AC,
所以四边形被分为两个三角形,
所以四边形ABCD的内角和为
180°×2=360°.
A
B
C
D
A
B
C
D
E
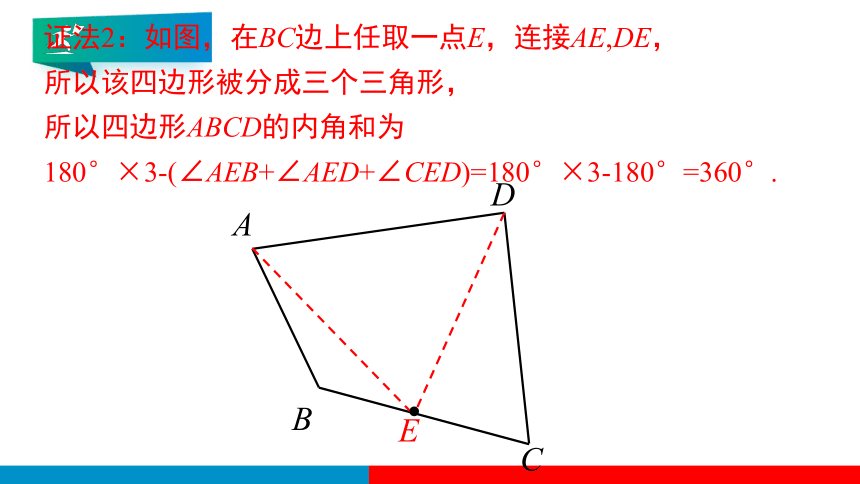
证法2:如图,在BC边上任取一点E,连接AE,DE,
所以该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3-(∠AEB+∠AED+∠CED)=180°×3-180°=360°.
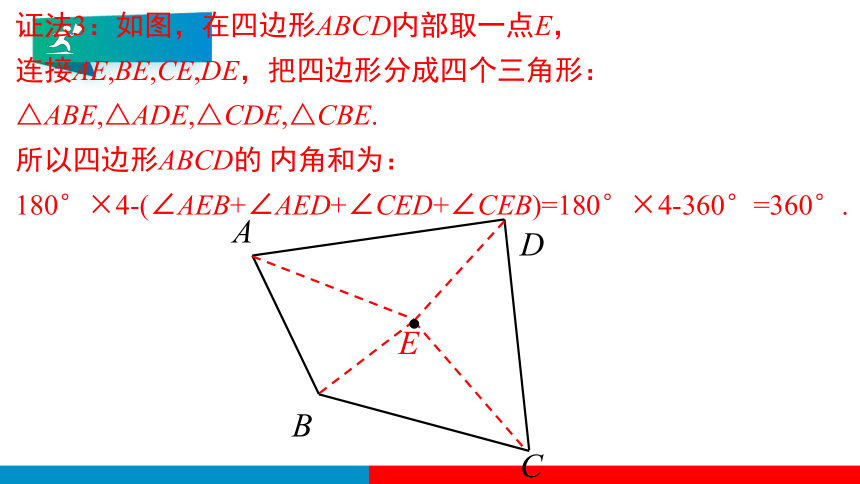
证法3:如图,在四边形ABCD内部取一点E,
连接AE,BE,CE,DE,把四边形分成四个三角形:△ABE,△ADE,△CDE,△CBE.
所以四边形ABCD的 内角和为:
180°×4-(∠AEB+∠AED+∠CED+∠CEB)=180°×4-360°=360°.
A
B
C
D
E
这几种方法都运用了转化思想,把四边形分割成三角形,转化到已经学过的三角形内角和求解.
结论: 四边形的内角和为360°.
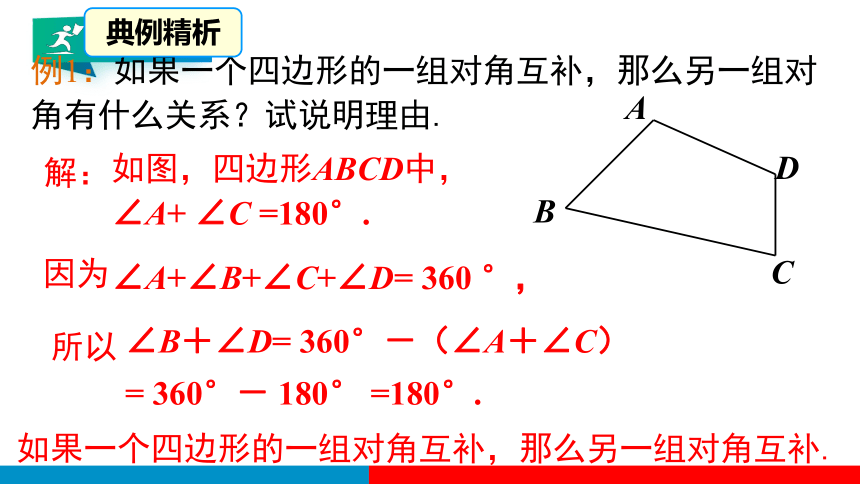
例1:如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:
如图,四边形ABCD中,∠A+ ∠C =180°.
∠A+∠B+∠C+∠D= 360 °,
因为
∠B+∠D= 360°-(∠A+∠C)
= 360°- 180° =180°.
所以
A
B
C
D
如果一个四边形的一组对角互补,那么另一组对角互补.
典例精析
A
C
D
E
B
A
B
C
D
E
F
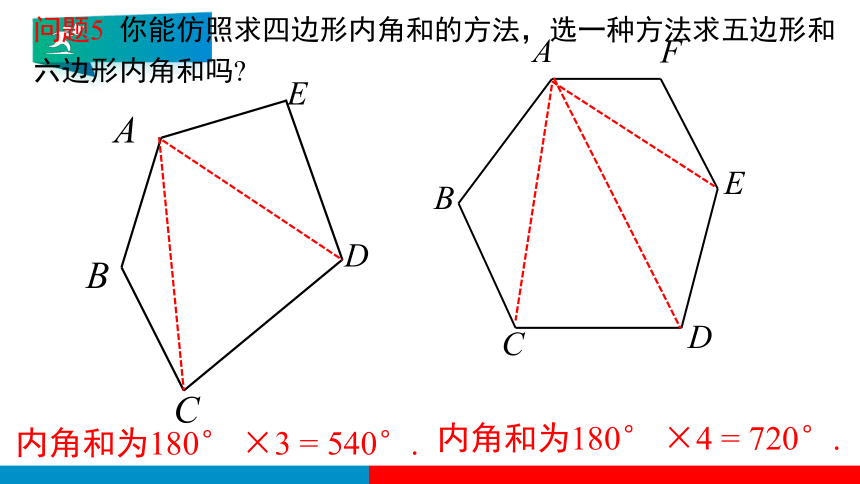
问题5 你能仿照求四边形内角和的方法,选一种方法求五边形和
六边形内角和吗
内角和为180° ×3 = 540°.
内角和为180° ×4 = 720°.
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
多边形
······
0
n -3
1
2
3
1
2
3
4
n -2
( n -2 )·180
1×180 =180
2×180 =360
3×180 =540
4×180 =720
······
······
······
······
由特殊到一般
分割
多边形
三角形
分割点与多边形的位置关系
顶点
边上
内部
转化思想
总结归纳
多边形的内角和公式
n边形的内角和等于(n-2)×180 °.
1. 定理 n 边形内角和等于(n-2)×180°(n ≥ 3).
2. 多边形内角和公式的常见应用
(1)已知多边形的边数,求内角和;
(2)已知多边形的内角和,求边数;
(3)求正n 边形每个内角的度数, 其公式为 ;
(4)已知n 边形每个内角的度数,且度数都相等,求边数.
例2 一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,则这个多边形的每个内角是多少度?
解:设这个多边形边数为n,
则(n-2) 180=360+720,
解得n=8,
∵这个多边形的每个内角都相等,
(8-2)×180°=1080°,
∴它每一个内角的度数为1080°÷8=135°.
典例精析
例3 已知n边形的内角和θ=(n-2)×180°.
甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,请说明理由;
解:∵360°÷180°=2,
630°÷180°=3......90°,
∴甲的说法对,乙的说法不对,
360°÷180°+2=4.
故甲同学说的边数n是4.
【变式题】一个同学在进行多边形的内角和计算时,求得内角和为1125°,当他发现错了以后,重新检查,发现少算了一个内角,问这个内角是多少度?他求的是几边形的内角和?
解:设此多边形的内角和为x,
则有1125°<x<1125°+180°,
即180°×6+45°<x<180°×7+45°.
因为x为多边形的内角和,所以它是180°的倍数,
所以x=180°×7=1260°.
所以7+2=9,1260°-1125°=135°.
因此,漏加的这个内角是135°,这个多边形是九边形.
思路点拨:多边形的内角的度数在0°~180°之间.
1.一个多边形的内角和不可能是( )
A.1800° B.540 ° C.720 ° D.810 °
D
2.一个多边形从一个顶点可引对角线3条,则这个多边形的 内角和等于( )
A.360° B.540 ° C.720 ° D.900 °
C
练习题
3. 一个多边形的内角和为1800°,截去一个角后,求得到的多边形的内角和.
解:∵1800÷180=10,
∴原多边形边数为10+2=12.
∵一个多边形截去一个内角后,边数可能减1,可能不变,也可能加1,
∴新多边形的边数可能是11,12,13,
∴新多边形的内角和可能是1620°,1800°,1980°.
4.如图11.3-1,正五边形ABCDE 中,对角线AC 与边
DE 平行,求∠ BCA 的度数.
解题秘方:紧扣多边形的内角和公式及平行线的性质求出相关角的度数.
解:∵五边形ABCDE 是正五边形,
∴∠ BCD= ∠ D= 180°× =108° .
∵ AC ∥ DE,∴∠ ACD+ ∠ D=180° .
∴∠ ACD=180°-108° =72° .
∴∠ BCA= ∠ BCD-∠ ACD=108°-72° =36° .
40°
5. [中考· 邵阳] 如图, 在四边形ABCD中, A D ⊥ A B ,∠C=110°,它的一个外角∠ ADE=60°,则∠ B 的大小是________.
6.根据下列条件求多边形的边数:
(1)多边形的内角和是1 620°;
解题秘方:根据多边形内角和公式列出方程求解.
解:设多边形的边数为n,根据题意得:
(n-2)·180=1 620,
解得n=11. 故多边形的边数为11.
已知内角和,设出边数n,利用
内角和公式列出方程求边数n
(2)正多边形的每个内角均为120°.
解题秘方:根据多边形内角和公式列出方程求解.
解:(n-2)·180=120n,
解得n=6. 故正多边形的边数为6.
https://www.21cnjy.com/help/help_extract.php
11.3 多边形及其内角和
11.3.2 多边形的内角和
精品同步教学课件
情景引入
思考:你知道正六边形的内角和是多少吗?
问题2 你知道长方形和正方形的内角和是多少度吗?
问题1 三角形内角和是多少度?
三角形内角和 是180°.
都是360°.
问题3 猜想任意四边形的内角和是多少度?
多边形的内角和
一
猜想:四边形ABCD的内角和是360°.
问题4 你能用以前学过的知识说明一下你的结论吗?
猜想与证明
证法1:如图,连接AC,
所以四边形被分为两个三角形,
所以四边形ABCD的内角和为
180°×2=360°.
A
B
C
D
A
B
C
D
E
证法2:如图,在BC边上任取一点E,连接AE,DE,
所以该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3-(∠AEB+∠AED+∠CED)=180°×3-180°=360°.
证法3:如图,在四边形ABCD内部取一点E,
连接AE,BE,CE,DE,把四边形分成四个三角形:△ABE,△ADE,△CDE,△CBE.
所以四边形ABCD的 内角和为:
180°×4-(∠AEB+∠AED+∠CED+∠CEB)=180°×4-360°=360°.
A
B
C
D
E
这几种方法都运用了转化思想,把四边形分割成三角形,转化到已经学过的三角形内角和求解.
结论: 四边形的内角和为360°.
例1:如果一个四边形的一组对角互补,那么另一组对角有什么关系?试说明理由.
解:
如图,四边形ABCD中,∠A+ ∠C =180°.
∠A+∠B+∠C+∠D= 360 °,
因为
∠B+∠D= 360°-(∠A+∠C)
= 360°- 180° =180°.
所以
A
B
C
D
如果一个四边形的一组对角互补,那么另一组对角互补.
典例精析
A
C
D
E
B
A
B
C
D
E
F
问题5 你能仿照求四边形内角和的方法,选一种方法求五边形和
六边形内角和吗
内角和为180° ×3 = 540°.
内角和为180° ×4 = 720°.
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
多边形
······
0
n -3
1
2
3
1
2
3
4
n -2
( n -2 )·180
1×180 =180
2×180 =360
3×180 =540
4×180 =720
······
······
······
······
由特殊到一般
分割
多边形
三角形
分割点与多边形的位置关系
顶点
边上
内部
转化思想
总结归纳
多边形的内角和公式
n边形的内角和等于(n-2)×180 °.
1. 定理 n 边形内角和等于(n-2)×180°(n ≥ 3).
2. 多边形内角和公式的常见应用
(1)已知多边形的边数,求内角和;
(2)已知多边形的内角和,求边数;
(3)求正n 边形每个内角的度数, 其公式为 ;
(4)已知n 边形每个内角的度数,且度数都相等,求边数.
例2 一个多边形的内角和比四边形的内角和多720°,并且这个多边形的各内角都相等,则这个多边形的每个内角是多少度?
解:设这个多边形边数为n,
则(n-2) 180=360+720,
解得n=8,
∵这个多边形的每个内角都相等,
(8-2)×180°=1080°,
∴它每一个内角的度数为1080°÷8=135°.
典例精析
例3 已知n边形的内角和θ=(n-2)×180°.
甲同学说,θ能取360°;而乙同学说,θ也能取630°.甲、乙的说法对吗?若对,求出边数n.若不对,请说明理由;
解:∵360°÷180°=2,
630°÷180°=3......90°,
∴甲的说法对,乙的说法不对,
360°÷180°+2=4.
故甲同学说的边数n是4.
【变式题】一个同学在进行多边形的内角和计算时,求得内角和为1125°,当他发现错了以后,重新检查,发现少算了一个内角,问这个内角是多少度?他求的是几边形的内角和?
解:设此多边形的内角和为x,
则有1125°<x<1125°+180°,
即180°×6+45°<x<180°×7+45°.
因为x为多边形的内角和,所以它是180°的倍数,
所以x=180°×7=1260°.
所以7+2=9,1260°-1125°=135°.
因此,漏加的这个内角是135°,这个多边形是九边形.
思路点拨:多边形的内角的度数在0°~180°之间.
1.一个多边形的内角和不可能是( )
A.1800° B.540 ° C.720 ° D.810 °
D
2.一个多边形从一个顶点可引对角线3条,则这个多边形的 内角和等于( )
A.360° B.540 ° C.720 ° D.900 °
C
练习题
3. 一个多边形的内角和为1800°,截去一个角后,求得到的多边形的内角和.
解:∵1800÷180=10,
∴原多边形边数为10+2=12.
∵一个多边形截去一个内角后,边数可能减1,可能不变,也可能加1,
∴新多边形的边数可能是11,12,13,
∴新多边形的内角和可能是1620°,1800°,1980°.
4.如图11.3-1,正五边形ABCDE 中,对角线AC 与边
DE 平行,求∠ BCA 的度数.
解题秘方:紧扣多边形的内角和公式及平行线的性质求出相关角的度数.
解:∵五边形ABCDE 是正五边形,
∴∠ BCD= ∠ D= 180°× =108° .
∵ AC ∥ DE,∴∠ ACD+ ∠ D=180° .
∴∠ ACD=180°-108° =72° .
∴∠ BCA= ∠ BCD-∠ ACD=108°-72° =36° .
40°
5. [中考· 邵阳] 如图, 在四边形ABCD中, A D ⊥ A B ,∠C=110°,它的一个外角∠ ADE=60°,则∠ B 的大小是________.
6.根据下列条件求多边形的边数:
(1)多边形的内角和是1 620°;
解题秘方:根据多边形内角和公式列出方程求解.
解:设多边形的边数为n,根据题意得:
(n-2)·180=1 620,
解得n=11. 故多边形的边数为11.
已知内角和,设出边数n,利用
内角和公式列出方程求边数n
(2)正多边形的每个内角均为120°.
解题秘方:根据多边形内角和公式列出方程求解.
解:(n-2)·180=120n,
解得n=6. 故正多边形的边数为6.
https://www.21cnjy.com/help/help_extract.php
