17.3勾股定理 授课课件

(共16张PPT)
勾股定理
【八上 第十七章 特殊的三角形】
精品课程
EIGHT GRADE MATHEMATICS COURSEWARE VOLUME II
情景引入
01
石家庄科技馆
情景引入
01
你发现了什么现象？
情景引入
01
你得到什么结论？
a
b
c
c2
a2
b2
a2+b2=c2
猜想
02
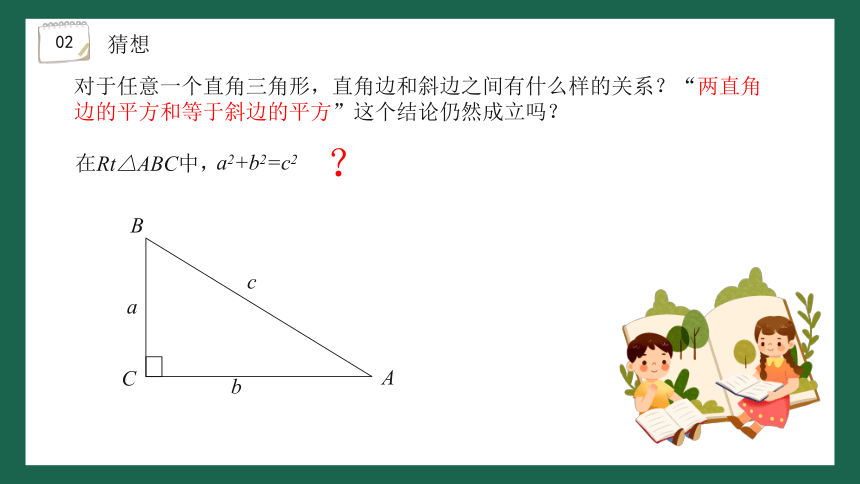
对于任意一个直角三角形，直角边和斜边之间有什么样的关系？“两直角边的平方和等于斜边的平方”这个结论仍然成立吗？
？
a2+b2=c2
在Rt△ABC中，
A
B
C
a
b
c
猜想
02
B
A
C
A
B
C
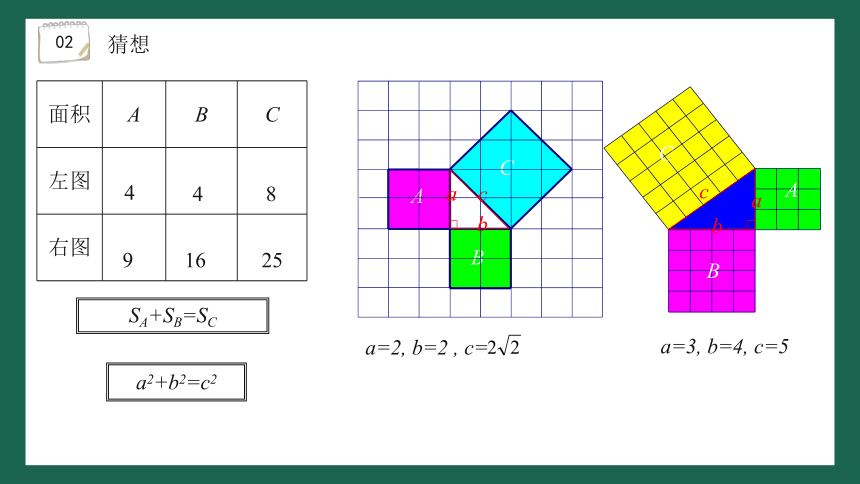
面积 A B C
左图
右图
16
9
8
4
25
SA+SB=SC
a
c
b
a
b
a=2, b=2 , c=
a=3, b=4, c=5
4
a2+b2=c2
c
证明
03
∴ a2+b2=c2
S大正方形＝4·S三角形＋S小正方形形
赵爽弦图
b-a
a2+b2=c2
在Rt△ABC中，
即，c2=4· ab+(b-a)2
c2=2ab+a2-2ab+b2
a
b
c
a
b
c
a
b
c
a
b
c
a
b
c
a
b
c
a
b
c
a
b
c
国际数学家大会会徽
证明
03
a2+b2=c2
在Rt△ABC中，
a
b
c
a
b
c
a
b
c
a
b
c
a
b
c
a
b
c
a
b
c
a
b
c
∵S大正方形 =S小正方形 +4SRt△
∴(a+b)2=c2+4 × ab
即
a2+b2=c2
构造法和等面积法
邹元治证明法
证明
03
∵S梯形=S等腰Rt △ +2SRt△
∴ (a+b)2= c2+2× ab
即
a2+b2=c2
总统证法
a2+b2=c2
在Rt△ABC中，
a
b
c
a
b
c
a
b
c
a
b
c
A
B
C
a
b
c
结论
04
直角三角形两直角边的平方和等于斜边的平方
勾股定理：
勾
股
（又称“毕达哥拉斯定理”）
弦
勾
股
几何语言：
∴a2+b2=c2
∵在Rt△ABC中，∠C=900
勾股定理的简单应用
05
例1.Rt△ABC中，∠C=90°，若a=6，c=10，则b=____.
例2.Rt△ABC中，∠C=90°，若a:b=3:4,c=10,则a=___，b=___.0，则a=___，b=___.
例3.Rt△ABC中，∠C=90°，若a=12，b=5，则斜边c上的高h= .
8
∵在Rt△ABC中，
a2+b2=c2
解得，b=8或-8
∴62+b2=102
（舍）
∴b=8
A
B
C
a
b
c
勾股定理的简单应用
05
例1.Rt△ABC中，∠C=90°，若a=6，c=10，则b=____.
例2.Rt△ABC中，∠C=90°，若a:b=3:4,c=10,则a=___，b=___.0，则a=___，b=___.
例3.Rt△ABC中，∠C=90°，若a=12，b=5，则斜边c上的高h= .
8
8
6
∵在Rt△ABC中，
a2+b2=c2
设，a=3x,b=4x
解得，x=2或-2（舍）
∴x=2
∴a=3x=6,b=4x=8
∴(3x)2+(4x)2=(10)2
A
B
C
a
b
c
勾股定理的简单应用
05
例1.Rt△ABC中，∠C=90°，若a=6，c=10，则b=____.
例2.Rt△ABC中，∠C=90°，若a:b=3:4,c=10,则a=___，b=___.0，则a=___，b=___.
例3.Rt△ABC中，∠C=90°，若a=12，b=5，则斜边c上的高h= .
8
8
6
∵在Rt△ABC中，
a2+b2=c2
解得，c=13或-13（舍)
∴(12)2+52=c2
∴h=
∵ SRt △ABC = ab= ch
∴c=13
A
B
C
a
b
c
h
勾股定理的简单应用
05
例1.Rt△ABC中，∠C=90°，若a=6，c=10，则b=____.
例2.Rt△ABC中，∠C=90°，若a:b=3:4,c=10,则a=___，b=___.0，则a=___，b=___.
例3.Rt△ABC中，∠C=90°，若a=12，b=5，则斜边c上的高h= .
8
8
6
方程
二次根式
等面积法
A
B
C
a
b
c
PART 03
课后回顾
勾股定理的证明
01
勾股定理的内容
02
勾股定理的简单应用
03
勾股定理的应用
【下节预告】
第十七中学 高红帆
EIGHT GRADE MATHEMATICS COURSEWARE VOLUME II