人教A版2019选择性必修第一册2.1.2两条直线平行与垂直的判定 课件(共20张ppt)
文档属性
| 名称 | 人教A版2019选择性必修第一册2.1.2两条直线平行与垂直的判定 课件(共20张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-01 20:13:06 | ||
图片预览







文档简介
(共20张PPT)
直线和圆的方程
2.1.2两条直线平行与垂直的判定
2.1 直线的倾斜角与斜率
课程标准
通过直观感受两条直线的位置关系,初步了解利用直线的斜率判断直线的平行与垂直的方法。进一步体会利用代数方法研究几何问题的基本方法,感受数形结合思想与化归转化思想。
复习回顾
问题1 直线的斜率定义与斜率公式是什么?
直线的倾斜角范围是:
新课导入
导
从数的角度刻画了直线相对于轴的倾斜程度,并导出了用直线上任意两点的坐标计算斜率的公式,从而把几何问题转化为代数问题。
为了在平面直角坐标系中用代数方法表示直线
利用倾斜角与直线上点的坐标关系引入直线的斜率
确定直线位置的几何要素
直线的倾斜角
下面,我们通过直线的斜率判断两条直线的位置关系.
一
二
三
教学目标
掌握两条直线的位置关系的判定
学会用直线的斜率判断直线的平行与垂直的条件
在探究直线的斜率过程中,掌握利用代数方法研究几何问题的解析几何的基本方法
教学目标
难点
重点
新知探究
探究一:能够利用直线的斜率判断直线的平行
新知讲解
问题2 平面中,两条直线的位置关系有哪些?
相交、平行
下面我们一起来探究平面中两条直线特殊的位置关系:垂直、平行
若没有特别说明,说“两条直线l1 , l2”时,指两条不重合的直线.
新知讲解
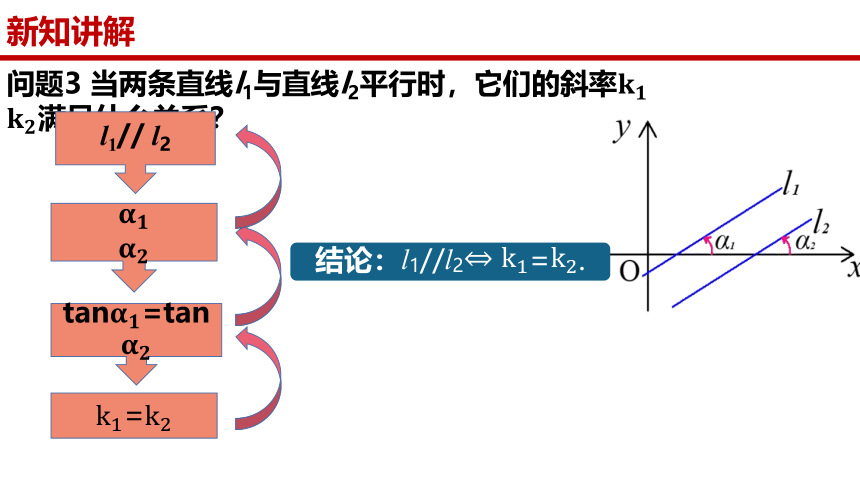
问题3 当两条直线l1与直线l2平行时,它们的斜率满足什么关系?
l1// l2
tan=tan
=
结论:l1//l2=.
概念生成
.
(1)当==90°时,直线的斜率不存在,此时.
(2)若直线重合,此时仍然有=.
(3)用斜率证明三点共线时,常常用到这个结论.
课堂练习
例1 已知试判断直线与的位置关系,并证明你的结论.
课堂练习
例3 已知四边形的四个顶点分别为
,试判断四边形的形状,并给出证明.
如图,由已知可得
AB边所在直线的斜率,
CD边所在直线的斜率
BC边所在直线的斜率
DA边所在直线的斜率·
因为=, =,
所以AB//CD,BC//DA.
因此四边形ABCD是平行四边形.
l1//l2=
计算斜率进行判断
新知探究
探究二:能够利用直线的斜率判断直线的垂直
新知讲解
问题4 两条直线相交,它们之间的斜率有怎样的关系?
两条直线相交
斜率不相等
在相交的位置关系中,垂直是最特殊的情形
新知讲解
问题5 直线垂直时,它们的斜率除了不相等外,是否还有特殊的数量关系
请大家合作探究下:
的斜率分别为,。,有怎样的关系?
新知讲解
设两条直线的斜率分别为,,
则直线l1,l2的方向向量分别是,
即1.
也就是说,.
由上我们得到,如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于1;反之,如果两条直线的斜率之积等于1,那么它们互相垂直.
即
当直线或的倾斜角为90°时,若,则另一条直线的倾斜角为0°
课堂练习
例4 已知三点,试判断的形状.
解:直线 AB的斜率
直线PQ的斜率
因为=,
所以直线.
随堂练习
1.判断下列各对直线是否平行或垂直:
(1)经过两点的直线,与经过点且斜率为1的直线;
(2)经过两点的直线,与经过点且斜率为5的直线.
习题讲解
解析:(1)直线的斜率,直线的斜率,
,.
(2)直线的斜率,直线的斜率,
,
测
随堂练习
2.试确定m的值,使过两点的直线与过两点的直线:
(1)平行; (2)垂直.
解析:,.
(1)若,则,即,解得
(2)若,则,即,
解得.
小结
l1//l2=.
l1l2=1.
(1)两条直线平行,它们斜率有怎样的关系?
(2)两条直线垂直,它们斜率有怎样的关系?
(3)我们如何判断直线的位置关系?
数:计算直线的斜率进行判断
形:画图!
直线和圆的方程
2.1.2两条直线平行与垂直的判定
2.1 直线的倾斜角与斜率
课程标准
通过直观感受两条直线的位置关系,初步了解利用直线的斜率判断直线的平行与垂直的方法。进一步体会利用代数方法研究几何问题的基本方法,感受数形结合思想与化归转化思想。
复习回顾
问题1 直线的斜率定义与斜率公式是什么?
直线的倾斜角范围是:
新课导入
导
从数的角度刻画了直线相对于轴的倾斜程度,并导出了用直线上任意两点的坐标计算斜率的公式,从而把几何问题转化为代数问题。
为了在平面直角坐标系中用代数方法表示直线
利用倾斜角与直线上点的坐标关系引入直线的斜率
确定直线位置的几何要素
直线的倾斜角
下面,我们通过直线的斜率判断两条直线的位置关系.
一
二
三
教学目标
掌握两条直线的位置关系的判定
学会用直线的斜率判断直线的平行与垂直的条件
在探究直线的斜率过程中,掌握利用代数方法研究几何问题的解析几何的基本方法
教学目标
难点
重点
新知探究
探究一:能够利用直线的斜率判断直线的平行
新知讲解
问题2 平面中,两条直线的位置关系有哪些?
相交、平行
下面我们一起来探究平面中两条直线特殊的位置关系:垂直、平行
若没有特别说明,说“两条直线l1 , l2”时,指两条不重合的直线.
新知讲解
问题3 当两条直线l1与直线l2平行时,它们的斜率满足什么关系?
l1// l2
tan=tan
=
结论:l1//l2=.
概念生成
.
(1)当==90°时,直线的斜率不存在,此时.
(2)若直线重合,此时仍然有=.
(3)用斜率证明三点共线时,常常用到这个结论.
课堂练习
例1 已知试判断直线与的位置关系,并证明你的结论.
课堂练习
例3 已知四边形的四个顶点分别为
,试判断四边形的形状,并给出证明.
如图,由已知可得
AB边所在直线的斜率,
CD边所在直线的斜率
BC边所在直线的斜率
DA边所在直线的斜率·
因为=, =,
所以AB//CD,BC//DA.
因此四边形ABCD是平行四边形.
l1//l2=
计算斜率进行判断
新知探究
探究二:能够利用直线的斜率判断直线的垂直
新知讲解
问题4 两条直线相交,它们之间的斜率有怎样的关系?
两条直线相交
斜率不相等
在相交的位置关系中,垂直是最特殊的情形
新知讲解
问题5 直线垂直时,它们的斜率除了不相等外,是否还有特殊的数量关系
请大家合作探究下:
的斜率分别为,。,有怎样的关系?
新知讲解
设两条直线的斜率分别为,,
则直线l1,l2的方向向量分别是,
即1.
也就是说,.
由上我们得到,如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于1;反之,如果两条直线的斜率之积等于1,那么它们互相垂直.
即
当直线或的倾斜角为90°时,若,则另一条直线的倾斜角为0°
课堂练习
例4 已知三点,试判断的形状.
解:直线 AB的斜率
直线PQ的斜率
因为=,
所以直线.
随堂练习
1.判断下列各对直线是否平行或垂直:
(1)经过两点的直线,与经过点且斜率为1的直线;
(2)经过两点的直线,与经过点且斜率为5的直线.
习题讲解
解析:(1)直线的斜率,直线的斜率,
,.
(2)直线的斜率,直线的斜率,
,
测
随堂练习
2.试确定m的值,使过两点的直线与过两点的直线:
(1)平行; (2)垂直.
解析:,.
(1)若,则,即,解得
(2)若,则,即,
解得.
小结
l1//l2=.
l1l2=1.
(1)两条直线平行,它们斜率有怎样的关系?
(2)两条直线垂直,它们斜率有怎样的关系?
(3)我们如何判断直线的位置关系?
数:计算直线的斜率进行判断
形:画图!
