向量的概念及表示[下学期]
图片预览



文档简介
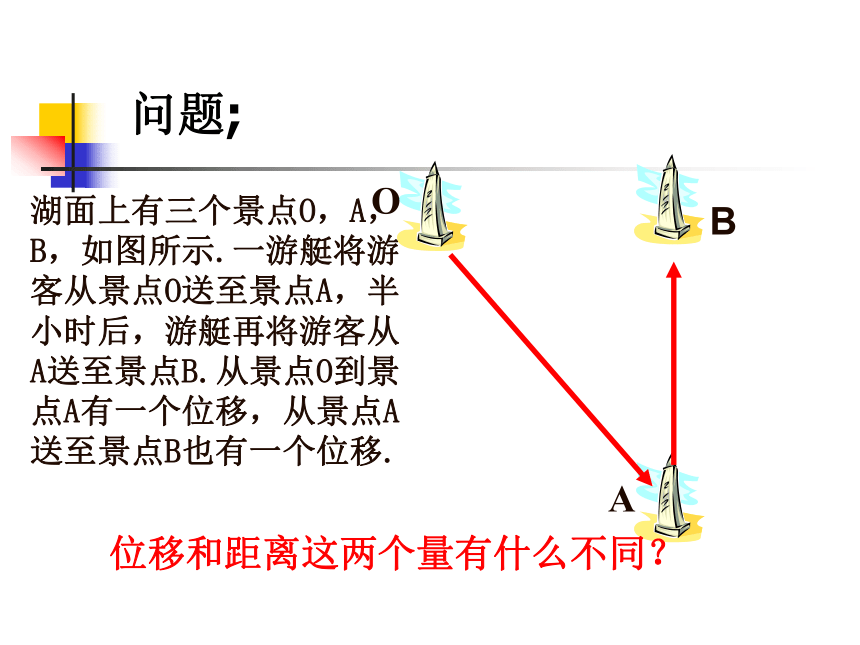
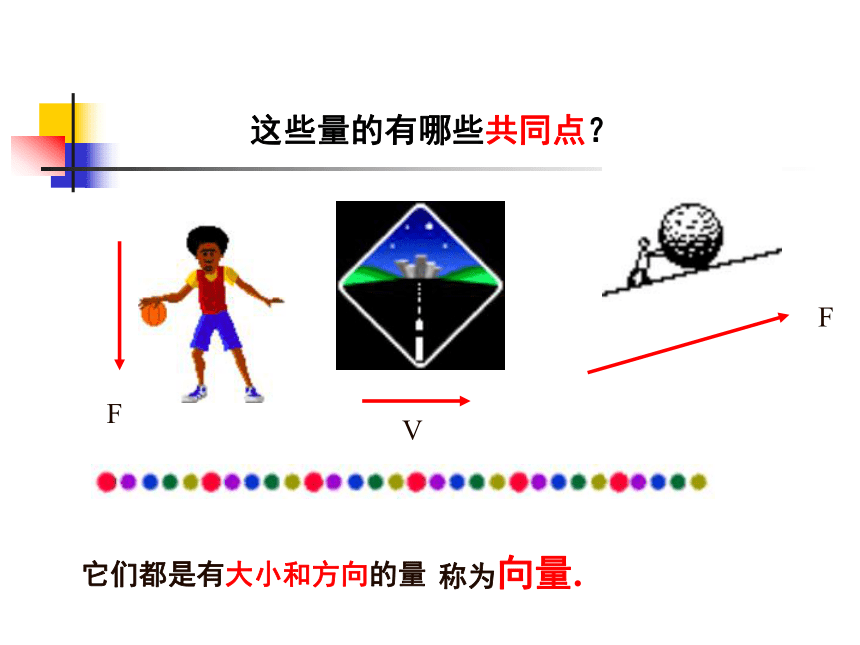
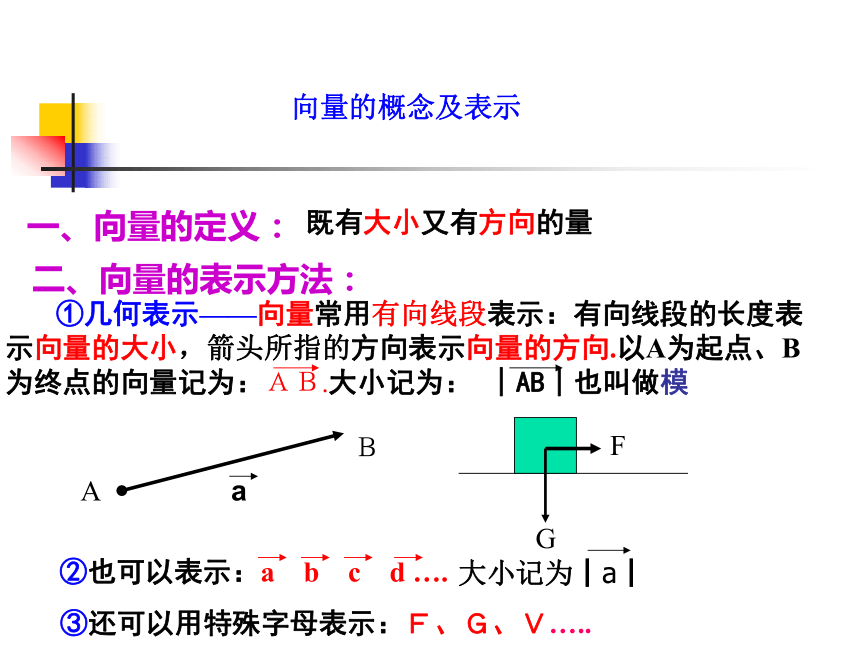
课件23张PPT。 §2.1向量的概念及表示江苏睢宁高级中学 朱虎 2006年3月湖面上有三个景点O,A,B,如图所示.一游艇将游客从景点O送至景点A,半小时后,游艇再将游客从A送至景点B.从景点O到景点A有一个位移,从景点A送至景点B也有一个位移.位移和距离这两个量有什么不同?问题;它们都是有大小和方向的量称为向量.这些量的有哪些共同点?二、向量的表示方法:③还可以用特殊字母表示:F、G、V….. 一、向量的定义:既有大小又有方向的量向量的概念及表示说明: 两个特殊向量注:0向量只有一个,而单位向量可以有无数个.:长度为 1 个单位长度的向量.思考:
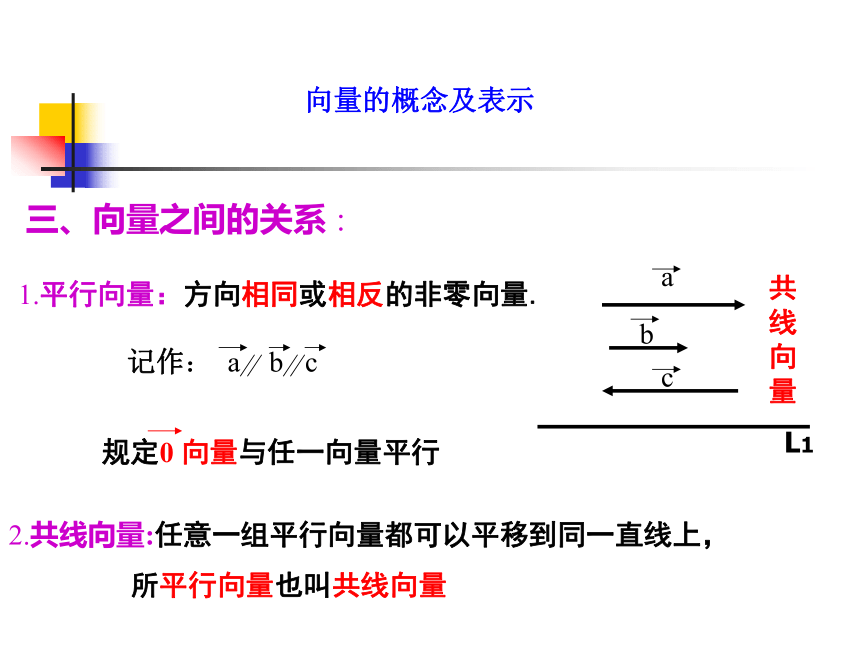
平面直角坐标系内,起点在原点的单位向量,它们的终点的轨迹是什么图形?向量的概念及表示三、向量之间的关系:共线向量1.平行向量:方向相同或相反的非零向量.2.共线向量:任意一组平行向量都可以平移到同一直线上,
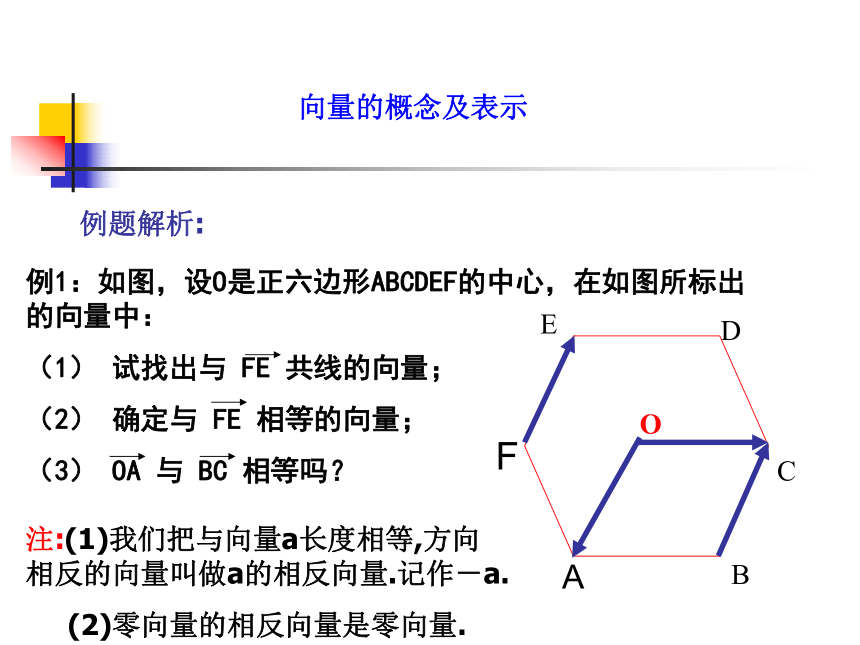
所平行向量也叫共线向量向量的概念及表示3.相等向量:V1=V2=V3=V4说明:在平行向量、共线向量、相等向量 的概念中应注意零向量的特殊性向量的概念及表示例题解析:向量的概念及表示注:(1)我们把与向量a长度相等,方向相反的向量叫做a的相反向量.记作-a.
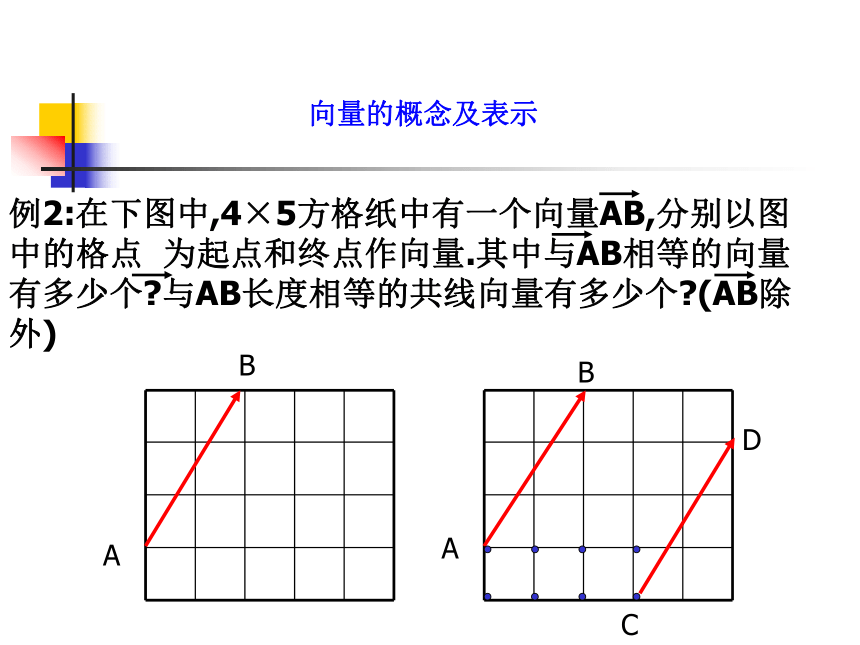
(2)零向量的相反向量是零向量.例2:在下图中,4×5方格纸中有一个向量AB,分别以图中的格点 为起点和终点作向量.其中与AB相等的向量有多少个?与AB长度相等的共线向量有多少个?(AB除外)ABABCD向量的概念及表示★题:★★★题:1234567891011★★题:过关竞技场向量的概念及表示练习1:
(1)单位向量是否一定相等?
(2)单位向量的大小是否一定相等?BACK不一定一定向量的概念及表示练习2:
(1)平行向量是否一定方向相同?
(2)不相等的向量一定不平行吗?BACK不一定不一定向量的概念及表示练习3
(1)与零向量相等的向量一定是什么向量?
(2)与任意向量都平行的向量是什么向量?零向量零向量向量的概念及表示BACKBACK练习4
(1)若两个向量在同一直线上,则这两个向量是什么向量?
(2)共线向量一定在一条直线上吗?共线向量 或者说平行向量不一定向量的概念及表示BACK练习5:
在质量、重力、速度、加速度、身高、面积、体积这些量中,哪些是数量?哪些是向量?数量有:质量、身高、面积、体积向量有:重力、速度、加速度向量的概念及表示在下列结论中,哪些是正确的?
(1)如果两个向量相等,那么它们的起点和终点分别重合;
(2)模相等的两个平行向量是相等的向量;
(3)如果两个向量是单位向量,那么它们相等;
(4)两个相等向量的模相等.正确的有:(4)向量的概念及表示练习6练习7:
1.设O为正△ABC的中心,则向量AO,BO,CO是 ( )
A.相等向量 B.模相等的向量
C.共线向量 D.共起点的向量
B向量的概念及表示BACK练习8:
1.已知a、b为不共线的非零向量,且存在向量 c,使 c ∥ a, c ∥ b, 则
c =____向量的概念及表示BACK练习9:
1.与非零向量a平行的向量中,
不相等的单位向量有_____个.2 向量的概念及表示练习10:如图,EF是△ABC的中位线,AD是BC 边是的中 线,在以A、B、C、D、E、F为端点的有向线
段表示的向量中请分别写出
(1)与向量CD共线的向量有___个,
分别是______________________;
(2)与向量DF的模一定相等的向
量有__个,分别是_________________;
(3)与向量DE相等的向量有__个,
分别是___________。 ABCDEFBACK752向量的概念及表示练习11如图,D、E、F分别是△ABC各边上的中点,四边形BCMF是平行四边形,请分别写出:
(1)与ED共线的向量;
(2)与FE共线的向量;
(3)与ED相等的向量;
(4)与FE相等的向量。BACK向量的概念及表示四、小结:
本节内容:向量的概念;向量的模;零向量、单位向量;
平行向量、共线向量、相等向量。五、课堂作业
P59 习题2.1 1、2、3。向量的概念及表示再见
平面直角坐标系内,起点在原点的单位向量,它们的终点的轨迹是什么图形?向量的概念及表示三、向量之间的关系:共线向量1.平行向量:方向相同或相反的非零向量.2.共线向量:任意一组平行向量都可以平移到同一直线上,
所平行向量也叫共线向量向量的概念及表示3.相等向量:V1=V2=V3=V4说明:在平行向量、共线向量、相等向量 的概念中应注意零向量的特殊性向量的概念及表示例题解析:向量的概念及表示注:(1)我们把与向量a长度相等,方向相反的向量叫做a的相反向量.记作-a.
(2)零向量的相反向量是零向量.例2:在下图中,4×5方格纸中有一个向量AB,分别以图中的格点 为起点和终点作向量.其中与AB相等的向量有多少个?与AB长度相等的共线向量有多少个?(AB除外)ABABCD向量的概念及表示★题:★★★题:1234567891011★★题:过关竞技场向量的概念及表示练习1:
(1)单位向量是否一定相等?
(2)单位向量的大小是否一定相等?BACK不一定一定向量的概念及表示练习2:
(1)平行向量是否一定方向相同?
(2)不相等的向量一定不平行吗?BACK不一定不一定向量的概念及表示练习3
(1)与零向量相等的向量一定是什么向量?
(2)与任意向量都平行的向量是什么向量?零向量零向量向量的概念及表示BACKBACK练习4
(1)若两个向量在同一直线上,则这两个向量是什么向量?
(2)共线向量一定在一条直线上吗?共线向量 或者说平行向量不一定向量的概念及表示BACK练习5:
在质量、重力、速度、加速度、身高、面积、体积这些量中,哪些是数量?哪些是向量?数量有:质量、身高、面积、体积向量有:重力、速度、加速度向量的概念及表示在下列结论中,哪些是正确的?
(1)如果两个向量相等,那么它们的起点和终点分别重合;
(2)模相等的两个平行向量是相等的向量;
(3)如果两个向量是单位向量,那么它们相等;
(4)两个相等向量的模相等.正确的有:(4)向量的概念及表示练习6练习7:
1.设O为正△ABC的中心,则向量AO,BO,CO是 ( )
A.相等向量 B.模相等的向量
C.共线向量 D.共起点的向量
B向量的概念及表示BACK练习8:
1.已知a、b为不共线的非零向量,且存在向量 c,使 c ∥ a, c ∥ b, 则
c =____向量的概念及表示BACK练习9:
1.与非零向量a平行的向量中,
不相等的单位向量有_____个.2 向量的概念及表示练习10:如图,EF是△ABC的中位线,AD是BC 边是的中 线,在以A、B、C、D、E、F为端点的有向线
段表示的向量中请分别写出
(1)与向量CD共线的向量有___个,
分别是______________________;
(2)与向量DF的模一定相等的向
量有__个,分别是_________________;
(3)与向量DE相等的向量有__个,
分别是___________。 ABCDEFBACK752向量的概念及表示练习11如图,D、E、F分别是△ABC各边上的中点,四边形BCMF是平行四边形,请分别写出:
(1)与ED共线的向量;
(2)与FE共线的向量;
(3)与ED相等的向量;
(4)与FE相等的向量。BACK向量的概念及表示四、小结:
本节内容:向量的概念;向量的模;零向量、单位向量;
平行向量、共线向量、相等向量。五、课堂作业
P59 习题2.1 1、2、3。向量的概念及表示再见
