11.3.2 多边形的内角和课件
文档属性
| 名称 | 11.3.2 多边形的内角和课件 |

|
|
| 格式 | ppt | ||
| 文件大小 | 141.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-09-04 00:00:00 | ||
图片预览


文档简介
(共10张PPT)
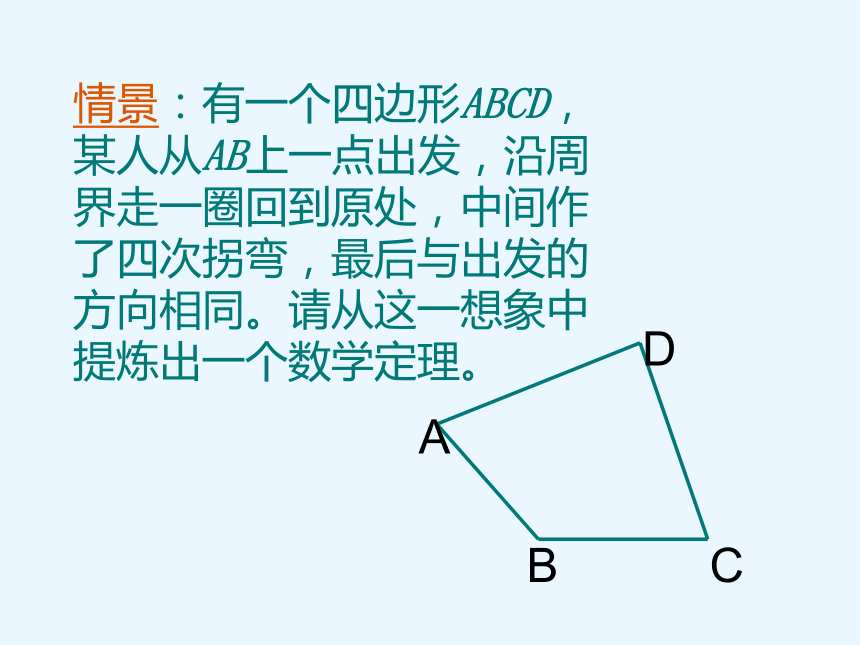
情景:有一个四边形ABCD,某人从AB上一点出发,沿周界走一圈回到原处,中间作了四次拐弯,最后与出发的方向相同。请从这一想象中提炼出一个数学定理。
A
B
C
D
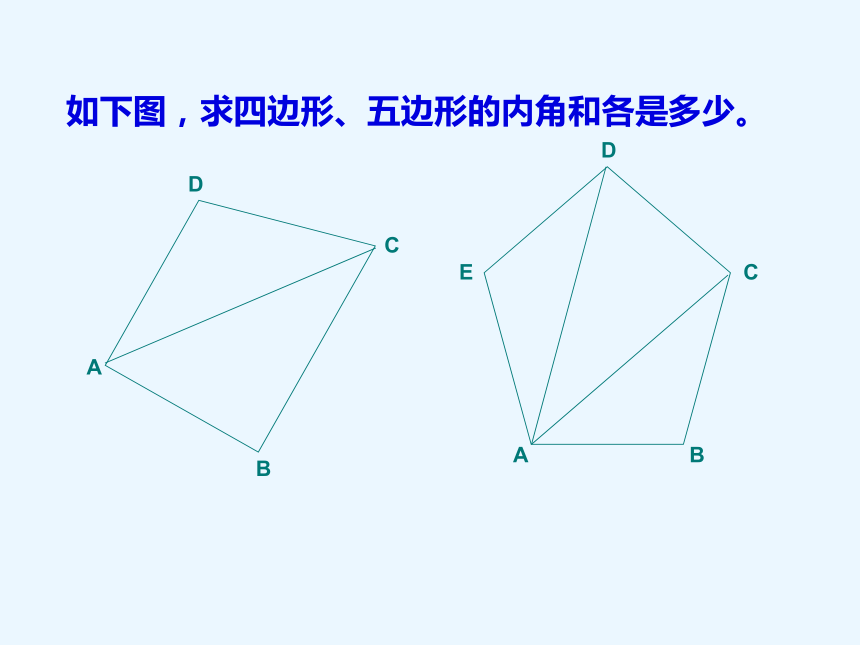
如下图,求四边形、五边形的内角和各是多少。
A
B
C
D
A
B
C
D
E
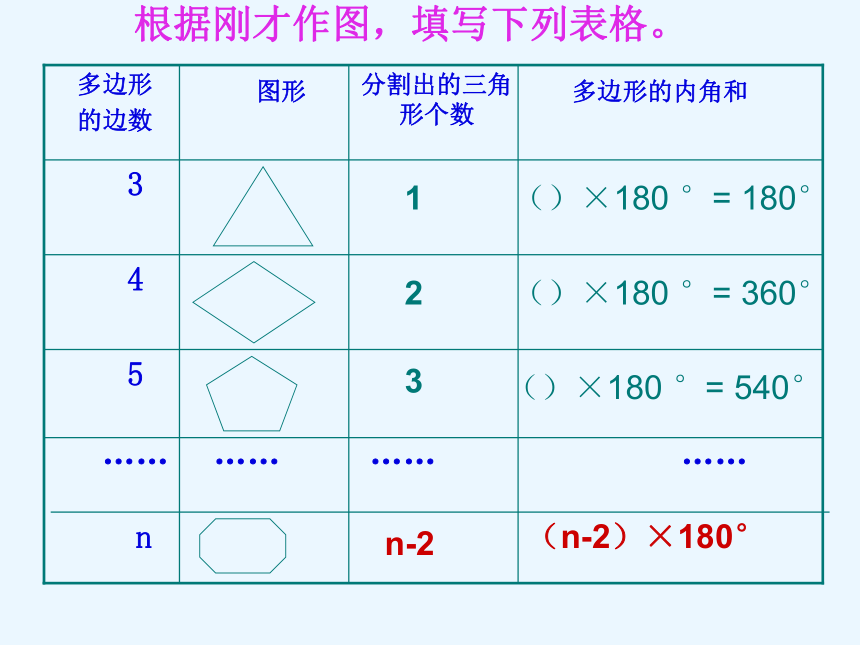
根据刚才作图,填写下列表格。
(n-2)×180°
n-2
n
……
……
……
……
()×180 °= 540°
3
5
()×180 °= 360°
2
4
()×180 °= 180°
1
3
多边形的内角和
分割出的三角形个数
图形
多边形
的边数
多边形内角和定理:
n边形内角和等于(n-2)·180°
下面请根据多边形内角和定理,给定一个n值
,编一道求多边形内角和的问题,然后同桌交换解
决问题。
求n边形的外角和。
多边形外角和等于360°。
1.判断题。
(1)当多边形边数增加时,它的内角和也随着增加。 ( )
(2)当多边形边数增加时,它的外角和也随着增加。 ( )
(3)三角形的外角和与八边形的外角和相等。 ( )
2.一个多边形的每一个外角都等于30度,它是几边形?
3.若一个多边形的每个外角都等于它的相邻的内角的1/2,求这个多边形的边数?
4.n边形的n个内角与其一个外角的总和为1350°,则这是个几边形?
1.本节课你学到了哪些知识,有什么收获?
2.本节课的学习中你用到了什么方法?
1 知识小结:这节课我们学习了n边形的内角和定理:
n边形的内角和等于(n-2)·180°及多边形的外角
和等于360°,其基本依据是三角形的三个内角和为
180°。
方法小结:在由三角形、四边形的内角和想象n
边形的内角和时,应用了由特殊到一般的归纳的思
想与方法;在依据公式编习题时,我们也进行了联
想,而“一般与特殊”,“正面与反面”等都是我
们进行联想的一些途径。
作业:教科书第页练习
第2、3题,
教科书第页习题7.3
第3、4、5、6、7题。
情景:有一个四边形ABCD,某人从AB上一点出发,沿周界走一圈回到原处,中间作了四次拐弯,最后与出发的方向相同。请从这一想象中提炼出一个数学定理。
A
B
C
D
如下图,求四边形、五边形的内角和各是多少。
A
B
C
D
A
B
C
D
E
根据刚才作图,填写下列表格。
(n-2)×180°
n-2
n
……
……
……
……
()×180 °= 540°
3
5
()×180 °= 360°
2
4
()×180 °= 180°
1
3
多边形的内角和
分割出的三角形个数
图形
多边形
的边数
多边形内角和定理:
n边形内角和等于(n-2)·180°
下面请根据多边形内角和定理,给定一个n值
,编一道求多边形内角和的问题,然后同桌交换解
决问题。
求n边形的外角和。
多边形外角和等于360°。
1.判断题。
(1)当多边形边数增加时,它的内角和也随着增加。 ( )
(2)当多边形边数增加时,它的外角和也随着增加。 ( )
(3)三角形的外角和与八边形的外角和相等。 ( )
2.一个多边形的每一个外角都等于30度,它是几边形?
3.若一个多边形的每个外角都等于它的相邻的内角的1/2,求这个多边形的边数?
4.n边形的n个内角与其一个外角的总和为1350°,则这是个几边形?
1.本节课你学到了哪些知识,有什么收获?
2.本节课的学习中你用到了什么方法?
1 知识小结:这节课我们学习了n边形的内角和定理:
n边形的内角和等于(n-2)·180°及多边形的外角
和等于360°,其基本依据是三角形的三个内角和为
180°。
方法小结:在由三角形、四边形的内角和想象n
边形的内角和时,应用了由特殊到一般的归纳的思
想与方法;在依据公式编习题时,我们也进行了联
想,而“一般与特殊”,“正面与反面”等都是我
们进行联想的一些途径。
作业:教科书第页练习
第2、3题,
教科书第页习题7.3
第3、4、5、6、7题。
