§2.3.2平面向量的坐标表示及运算[下学期]
文档属性
| 名称 | §2.3.2平面向量的坐标表示及运算[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 219.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-03-22 10:26:00 | ||
图片预览



文档简介
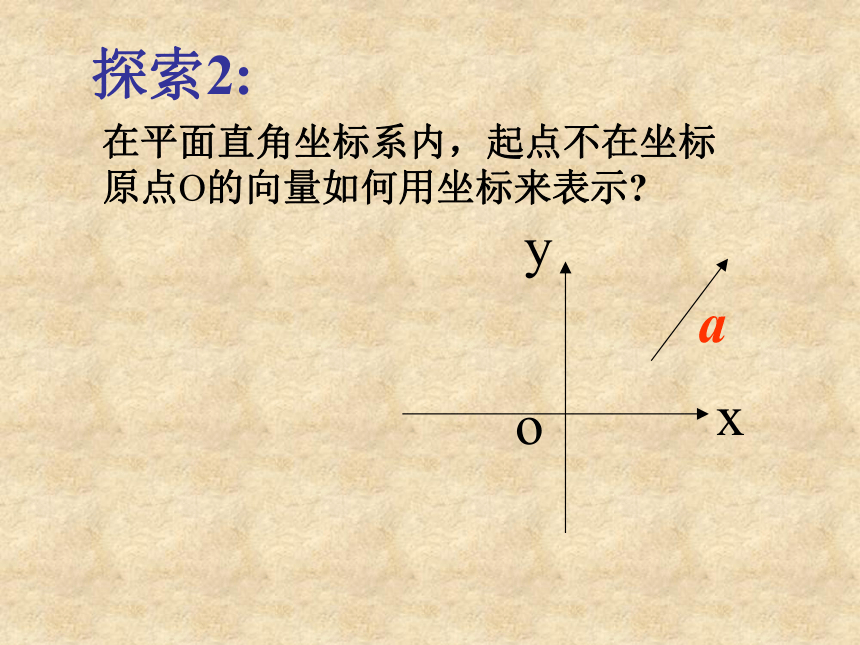
课件27张PPT。复 习1、平面向量基本定理的内容是什么? 2、什么是平面向量的基底?AB向量的坐标表示在平面直角坐标系内,起点不在坐标原点O的向量如何用坐标来表示?探索2:
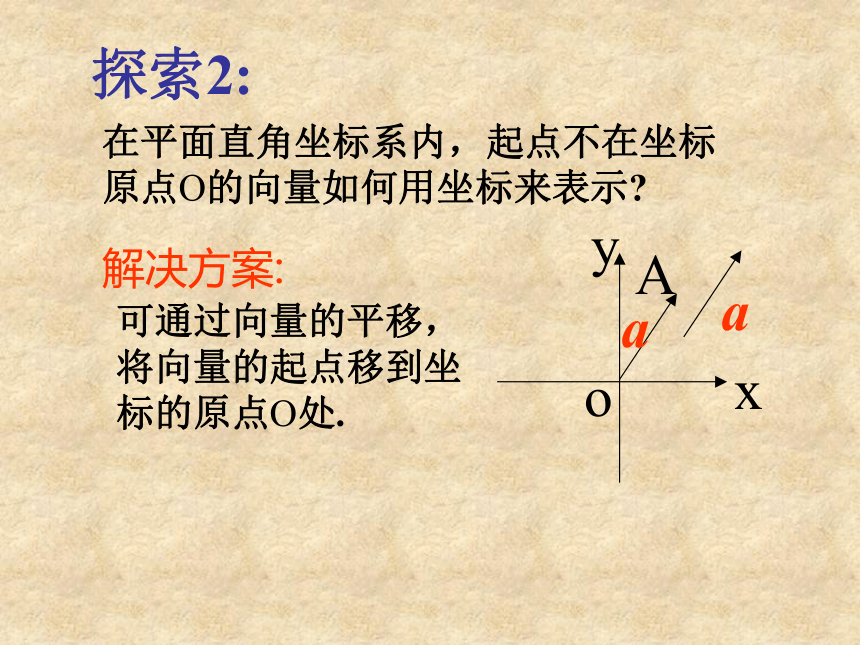
在平面直角坐标系内,起点不在坐标原点O的向量如何用坐标来表示?探索2:
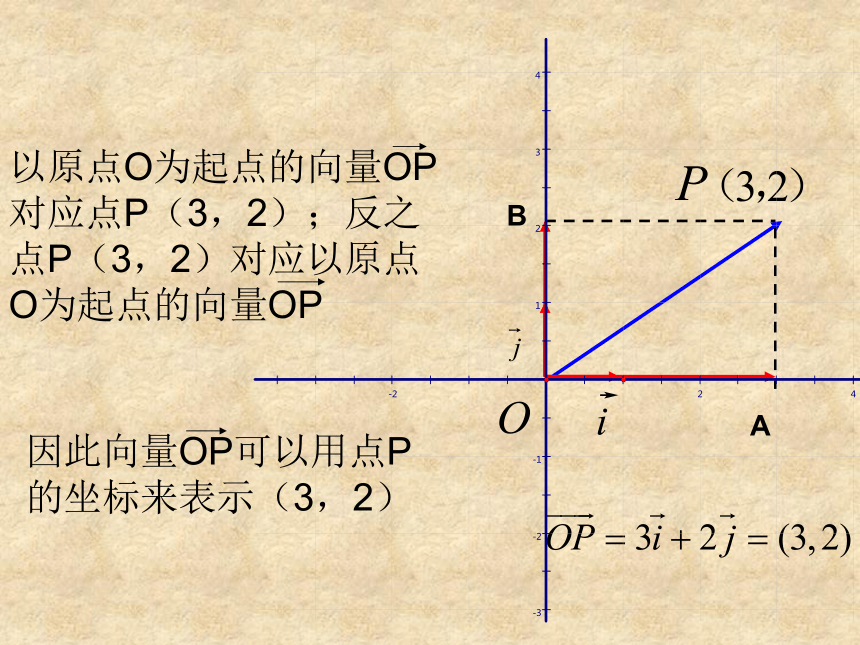
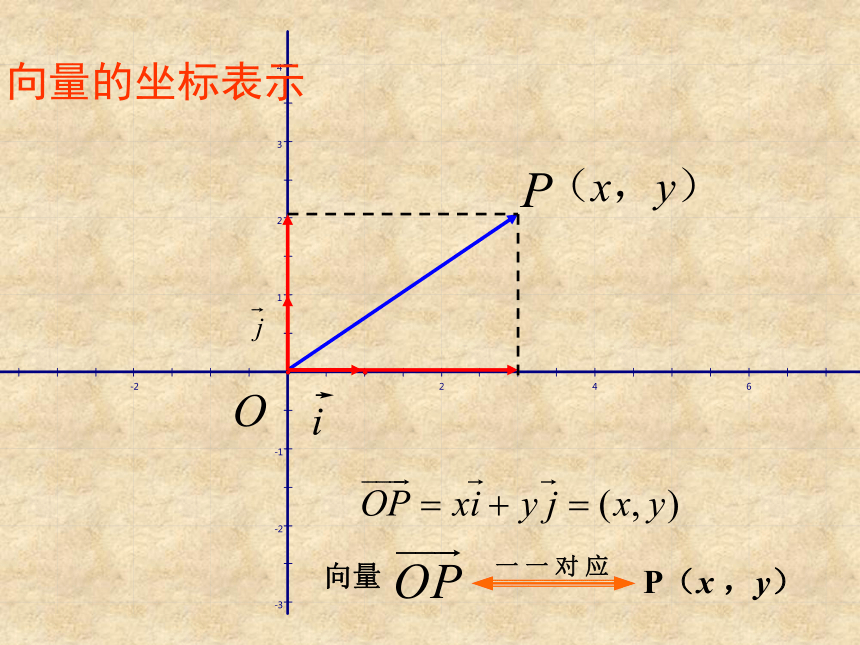
在平面直角坐标系内,我们分别取与X轴、Y轴方向相同的单位向量 i , j作为基底,任作一向量a,由平面向量基本定理知,有且仅有一对实数 x , y ,使得 a=x i+y j.定义:归纳总结解:设A(x,y)则
A练习:P74 1、2平面向量可以用坐标表示,向量的运算可以用坐标来运算吗?问题3: 如何计算? =( + )i+( + )j两个向量和与差的坐标分别等于这两向量想应坐标的和与差 实数与向量的积的坐标等于这个实数乘原来的向量的应坐标.向量的坐标运算探索4:已知 和 ,请问如何表示 ? O解:练习:P74 3、4课时小结:2 加、减法坐标运算法则.a + b=( x2 , y2) + (x1 ,? y1)= (x2+x1 , y2+y1)3 实数与向量积的坐标运算法则:λa =λ(x i+y j )=λx i+λy j =4 向量坐标.若A(x1 , y1) , B(x2 , y2)1 向量坐标定义.则 =(x2 - x1 , y2 – y1 ) a - b=( x2 , y2) - (x1 ,? y1)= (x2- x1 , y2-y1)解:设P(x,y)则变式:有向线段 的定比分点坐标公式与定比分值公式。 注意:特殊情况分析 你能根据P点的三种不同的位置和实数与向量的积的向量方向确定λ的取值范围吗? 总结:如何确定?值?思
考练习:P74 5、6、知 识 反 馈1、若向量 a 的起点坐标为(3,1),终点坐标为(-3,-1)求 a 的坐标. 3已知 =(x , y) , 点B的坐标为
(-2,1)求 的坐标.2、已知向量 =(6,1),
=(1 ,-3), =(-1,-2), 求向量 . 5.已知两点 , ,求点 分 所
成的比 及 y 的值. 解:由线段的定比分点坐标公式,得
解得由定比分点坐标公式可得G点坐标为:即点G的坐标为 (重心的坐标公式)重要结论,要求大家记忆!课时小结:2 加、减法坐标运算法则.a + b=( x2 , y2) + (x1 ,? y1)= (x2+x1 , y2+y1)3 实数与向量积的坐标运算法则:λa =λ(x i+y j )=λx i+λy j =4 向量坐标.若A(x1 , y1) , B(x2 , y2)1 向量坐标定义.则 =(x2 - x1 , y2 – y1 ) a - b=( x2 , y2) - (x1 ,? y1)= (x2- x1 , y2-y1)探索与研究 若平面的基底e1 , e2不垂直,是否可以研究此坐标系下向量的坐标?有兴趣的同学课后研究.
A练习:P74 1、2平面向量可以用坐标表示,向量的运算可以用坐标来运算吗?问题3: 如何计算? =( + )i+( + )j两个向量和与差的坐标分别等于这两向量想应坐标的和与差 实数与向量的积的坐标等于这个实数乘原来的向量的应坐标.向量的坐标运算探索4:已知 和 ,请问如何表示 ? O解:练习:P74 3、4课时小结:2 加、减法坐标运算法则.a + b=( x2 , y2) + (x1 ,? y1)= (x2+x1 , y2+y1)3 实数与向量积的坐标运算法则:λa =λ(x i+y j )=λx i+λy j =4 向量坐标.若A(x1 , y1) , B(x2 , y2)1 向量坐标定义.则 =(x2 - x1 , y2 – y1 ) a - b=( x2 , y2) - (x1 ,? y1)= (x2- x1 , y2-y1)解:设P(x,y)则变式:有向线段 的定比分点坐标公式与定比分值公式。 注意:特殊情况分析 你能根据P点的三种不同的位置和实数与向量的积的向量方向确定λ的取值范围吗? 总结:如何确定?值?思
考练习:P74 5、6、知 识 反 馈1、若向量 a 的起点坐标为(3,1),终点坐标为(-3,-1)求 a 的坐标. 3已知 =(x , y) , 点B的坐标为
(-2,1)求 的坐标.2、已知向量 =(6,1),
=(1 ,-3), =(-1,-2), 求向量 . 5.已知两点 , ,求点 分 所
成的比 及 y 的值. 解:由线段的定比分点坐标公式,得
解得由定比分点坐标公式可得G点坐标为:即点G的坐标为 (重心的坐标公式)重要结论,要求大家记忆!课时小结:2 加、减法坐标运算法则.a + b=( x2 , y2) + (x1 ,? y1)= (x2+x1 , y2+y1)3 实数与向量积的坐标运算法则:λa =λ(x i+y j )=λx i+λy j =4 向量坐标.若A(x1 , y1) , B(x2 , y2)1 向量坐标定义.则 =(x2 - x1 , y2 – y1 ) a - b=( x2 , y2) - (x1 ,? y1)= (x2- x1 , y2-y1)探索与研究 若平面的基底e1 , e2不垂直,是否可以研究此坐标系下向量的坐标?有兴趣的同学课后研究.
